STAT102: Business Data Analysis - Time Series and Correlation Analysis

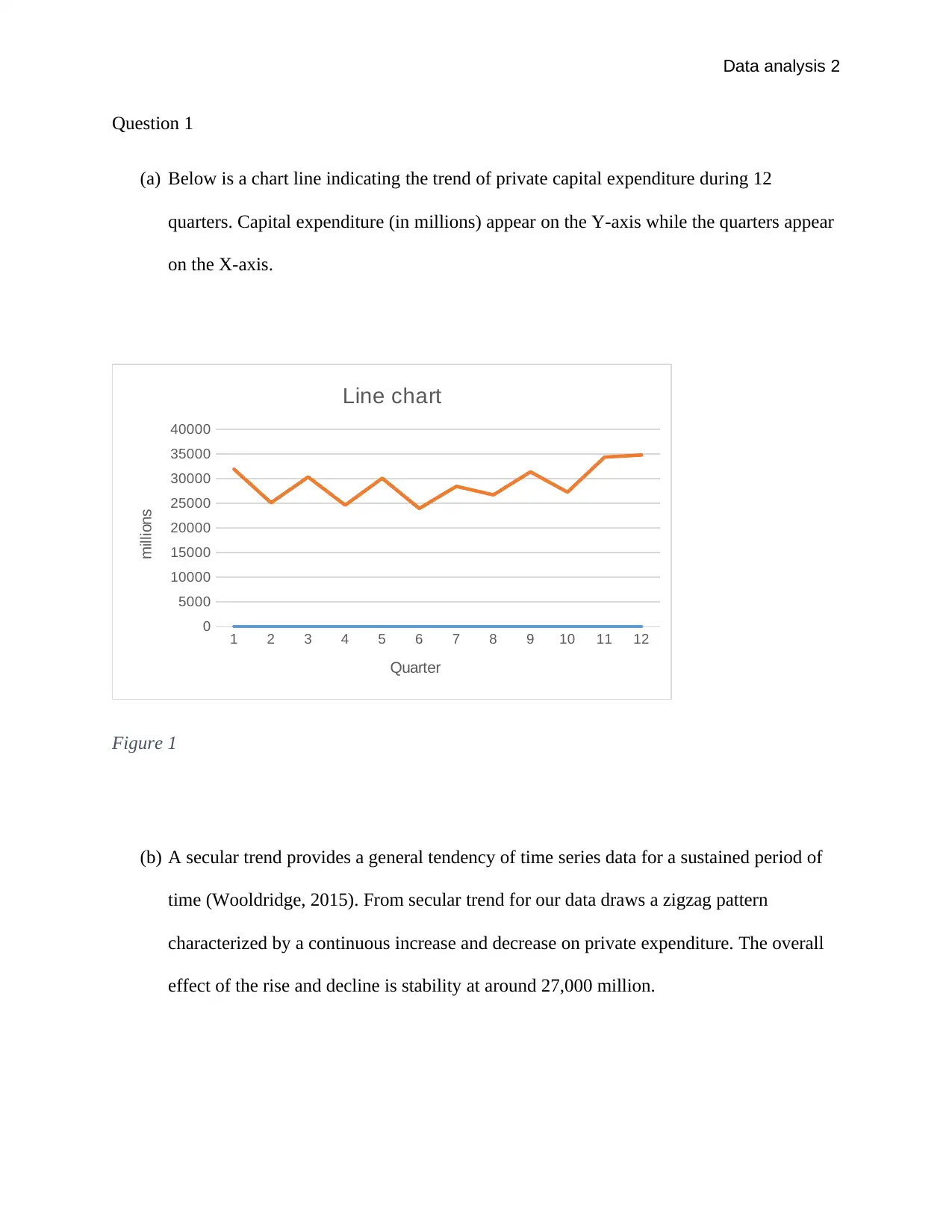
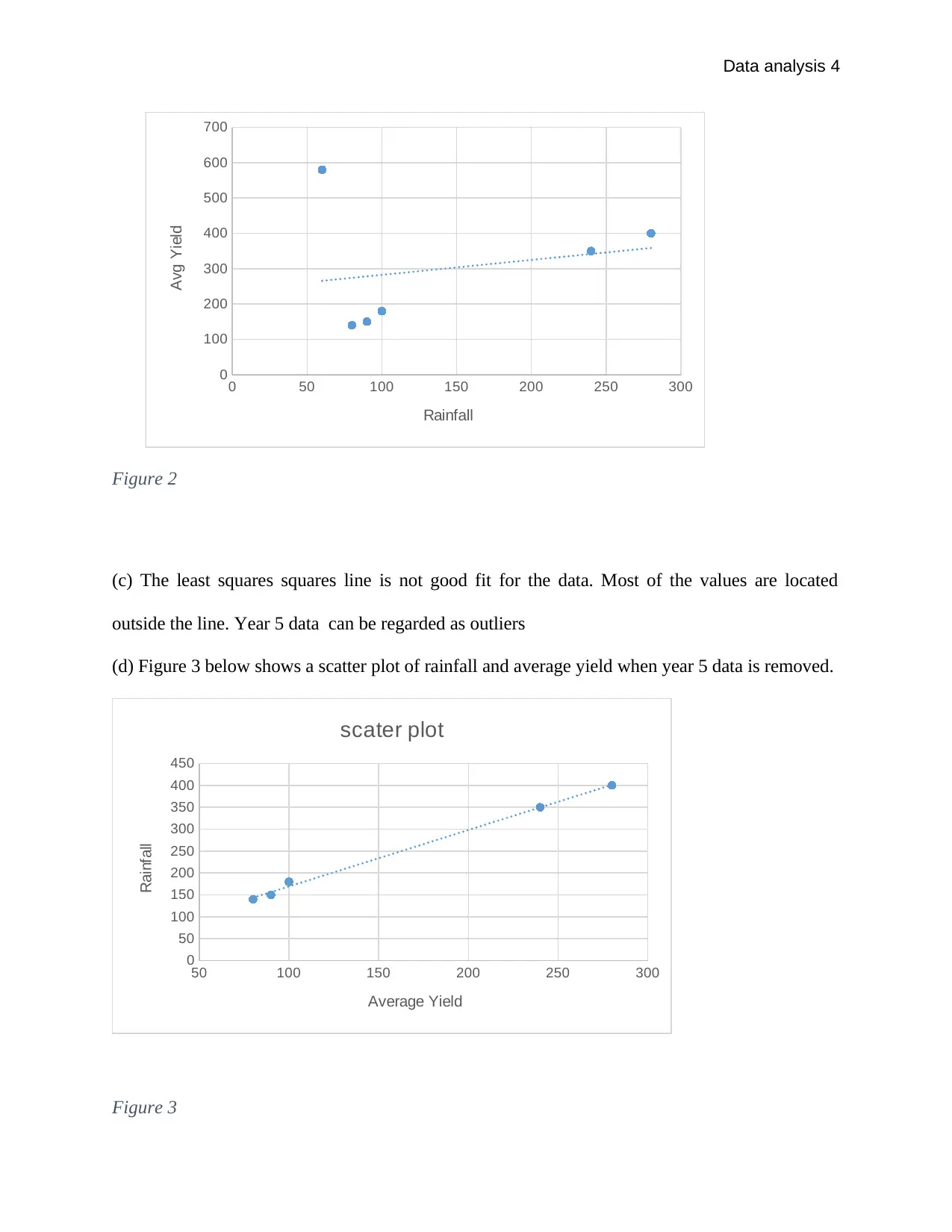
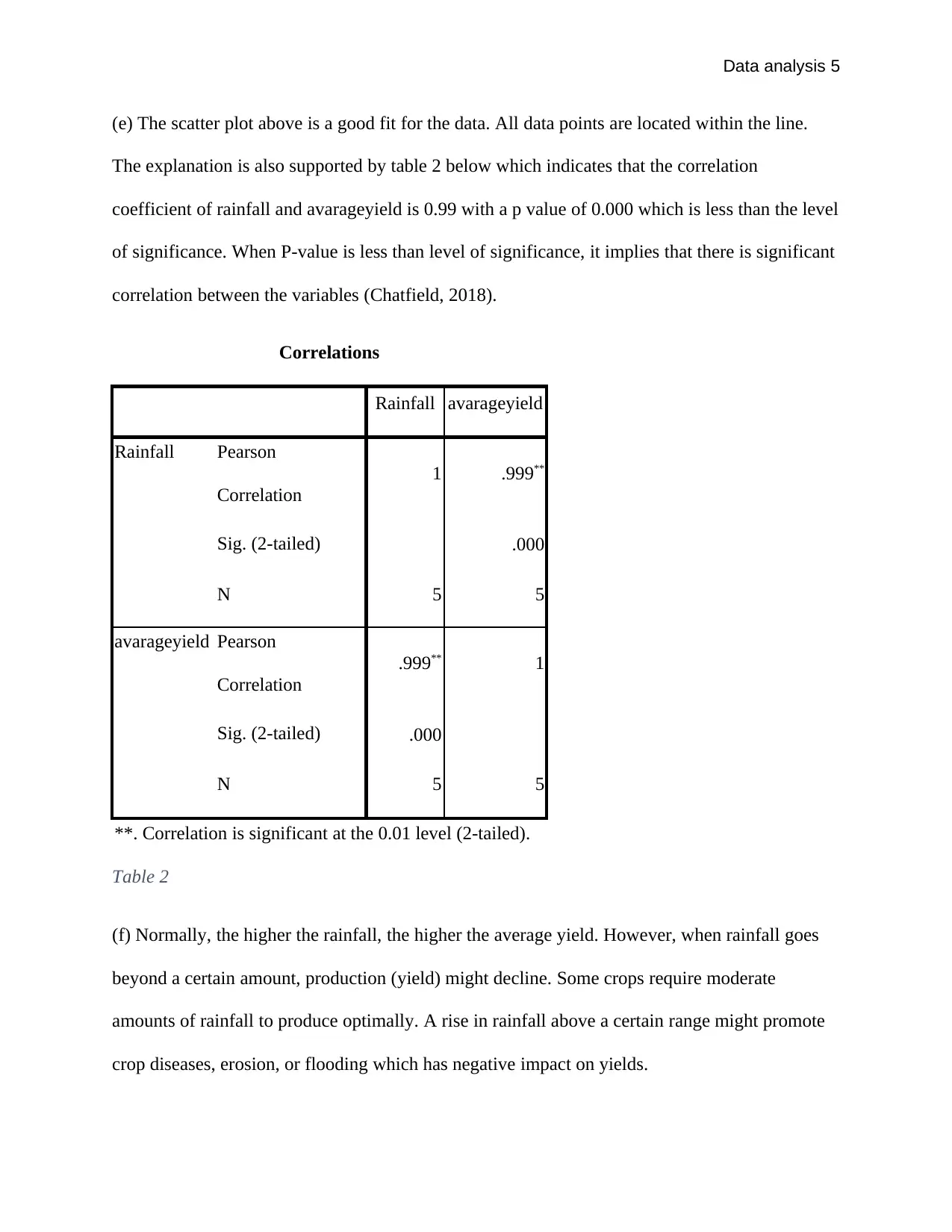
This assignment provides a detailed analysis of private capital expenditure using time series data over 12 quarters, including the creation of a line chart and commentary on secular and seasonal trends, with a prediction for Quarter 13. It further explores the relationship between average yield and rain...Read More

Data analysis 1
DATA ANALYSIS
By Name
Course
Instructor
Institution
Location
Date

Data analysis 2
Question 1
(a) Below is a chart line indicating the trend of private capital expenditure during 12
quarters. Capital expenditure (in millions) appear on the Y-axis while the quarters appear
on the X-axis.
1 2 3 4 5 6 7 8 9 10 11 12
0
5000
10000
15000
20000
25000
30000
35000
40000
Line chart
Quarter
millions
Figure 1
(b) A secular trend provides a general tendency of time series data for a sustained period of
time (Wooldridge, 2015). From secular trend for our data draws a zigzag pattern
characterized by a continuous increase and decrease on private expenditure. The overall
effect of the rise and decline is stability at around 27,000 million.

Data analysis 3
(c) The chart displays a seasonal trend. The chart contains periodic peaks and lows implying
that private capital expenditure is high during some period of the year and low during
other seasons.
(d) The expenditure at period Quarter 13 is likely to be 35,000 million. Extrapolating the
graph, it is evident that, expenditure is still rising towards point 35,000 million then it
would decline in response to the season.
Question 2
a) No. There is no linear relationship between average yield and rainfall. The correlation
between the 2 variables is 0.226. However, the significance level (0.667) is greater than 0.05
implying that there exist no linear correlation between average yield and rainfall.
Test of correlations
Rainfall avarageyield
Rainfall Pearson
Correlation
1 .226
Sig. (2-tailed) .667
N 6 6
Table 1
(b) Below is a scatter plot and least squares line showing relationship between average yield and
rainfall

Data analysis 4
0 50 100 150 200 250 300
0
100
200
300
400
500
600
700
Rainfall
Avg Yield
Figure 2
(c) The least squares squares line is not good fit for the data. Most of the values are located
outside the line. Year 5 data can be regarded as outliers
(d) Figure 3 below shows a scatter plot of rainfall and average yield when year 5 data is removed.
50 100 150 200 250 300
0
50
100
150
200
250
300
350
400
450
scater plot
Average Yield
Rainfall
Figure 3

Data analysis 5
(e) The scatter plot above is a good fit for the data. All data points are located within the line.
The explanation is also supported by table 2 below which indicates that the correlation
coefficient of rainfall and avarageyield is 0.99 with a p value of 0.000 which is less than the level
of significance. When P-value is less than level of significance, it implies that there is significant
correlation between the variables (Chatfield, 2018).
Correlations
Rainfall avarageyield
Rainfall Pearson
Correlation
1 .999**
Sig. (2-tailed) .000
N 5 5
avarageyield Pearson
Correlation
.999** 1
Sig. (2-tailed) .000
N 5 5
**. Correlation is significant at the 0.01 level (2-tailed).
Table 2
(f) Normally, the higher the rainfall, the higher the average yield. However, when rainfall goes
beyond a certain amount, production (yield) might decline. Some crops require moderate
amounts of rainfall to produce optimally. A rise in rainfall above a certain range might promote
crop diseases, erosion, or flooding which has negative impact on yields.

Data analysis 6
References
Chatfield, C. (2018) Introduction to multivariate analysis. Abingdon: Routledge.
Wooldridge, J.M. (2015) Introductory econometrics: A modern approach. Ontario: Nelson
Education.