Data Analysis Report of Fatalities in Australia

This report analyzes the trends in fatalities in Australia using various statistical techniques. It includes one-variable and two-variable analysis, clustering, and linear regression. The findings provide valuable insights for researchers, academia, and government in formulating policies.

Data analysis report of the fatalities in six Australian states as well as the two
territories
Prepared by
Firstname Lastname
University of the Sunshine Coast
Queensland
May-June 2019

1. Introduction
1.1 Authorization and Purpose
The main aim of this study was to analyze the fatality trends in 8 states within
Australia. The study did not have specific objectives, however the study reports any
interesting findings found during the analysis. The findings are crucial to the
researchers, academia and even the government in terms of formulating policies.
1.2 Limitations
This analysis focusses on one country only, which is Australia.
1.3 Scope
The study involves pre-processing of the secondary data obtained from the World
Bank database. Before embarking on data analysis, data cleaning was performed. 2
one-variable analyses and 2 two-variable analysis were performed as well as
advanced analysis involving cluster analysis as well as regression analysis with plots
were performed.
1.4 Methodology
This study utilizes data from World Bank database on fatalities. The datasets are
provided as csv files. A number of statistical techniques are employed to analyze the
data.
2. Data setup
Before the Data is loaded into R, the raw dataset on fatalities was pre-processed by
removing the first five rows that made no sense in analysis for easy use in R. The new
pre-processed data was then loaded into R software using the following command.
fatalities<-read.csv("C:\\
Users\\310187796\\
Documents\\fatalities.csv")

For the purposes of advanced analysis, the package ‘’cluster’’ was installed and loaded
into R workspace for cluster visualizations. The code for this is given below.
3. Exploratory Data analysis
3.1 One variable analysis
3.1.1 One variable analysis 1
The codes are presented below;
A summary statistics of the speed limit was performed and the
results showed that the avergae speed limit was 83.17 with the median speed being 80.00 while
the highest and the lowest speeds were 130.00 and 15.00 respectively.
A boxplot of speed limit was also plotted to check on the
distribution of the speed limit. As can be seen, the distribution of the speed limit is
approximately normally distributed.
install.packages("cluster")
library(cluster)
summary(Speed.Limit)
boxplot(Speed.Limit,
ylab="Speed Limit",
main="Boxplot of Speed
Limit", col="aquamarine")
> summary(Speed.Limit)
Min. 1st Qu. Median
Mean 3rd Qu. Max.
15.00 60.00 80.00
83.17 100.00 130.00

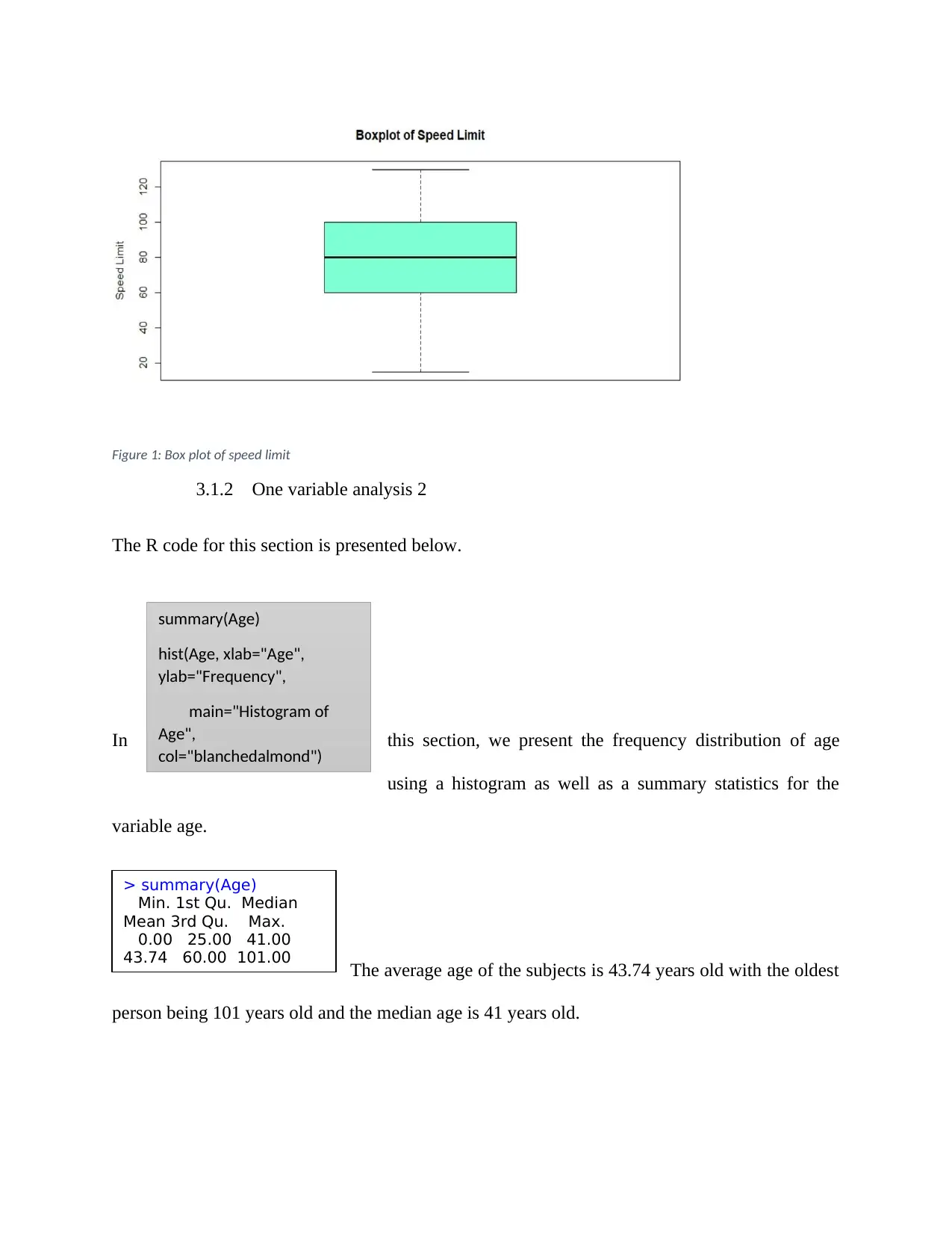
Figure 1: Box plot of speed limit
3.1.2 One variable analysis 2
The R code for this section is presented below.
In this section, we present the frequency distribution of age
using a histogram as well as a summary statistics for the
variable age.
The average age of the subjects is 43.74 years old with the oldest
person being 101 years old and the median age is 41 years old.
summary(Age)
hist(Age, xlab="Age",
ylab="Frequency",
main="Histogram of
Age",
col="blanchedalmond")
> summary(Age)
Min. 1st Qu. Median
Mean 3rd Qu. Max.
0.00 25.00 41.00
43.74 60.00 101.00

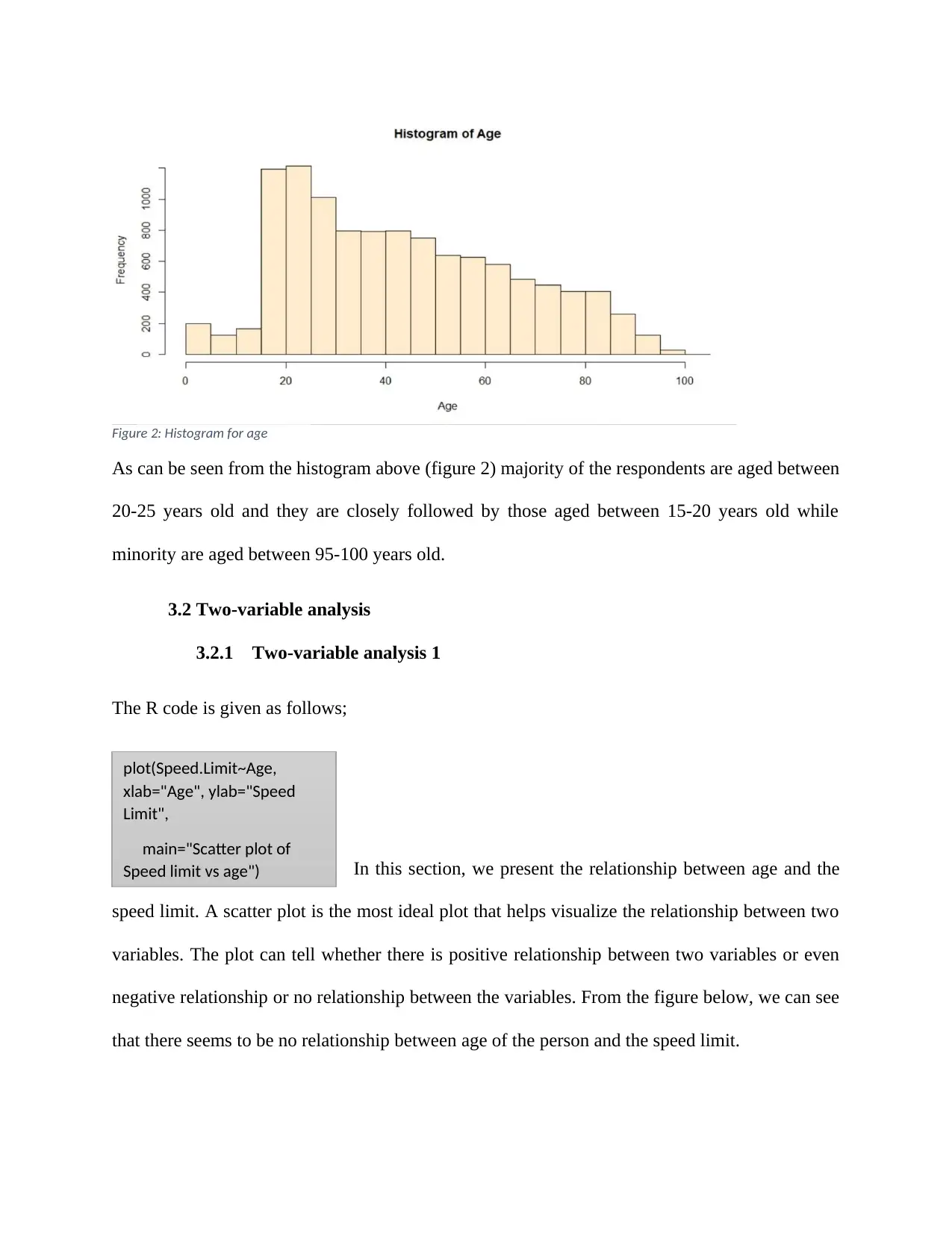
Figure 2: Histogram for age
As can be seen from the histogram above (figure 2) majority of the respondents are aged between
20-25 years old and they are closely followed by those aged between 15-20 years old while
minority are aged between 95-100 years old.
3.2 Two-variable analysis
3.2.1 Two-variable analysis 1
The R code is given as follows;
In this section, we present the relationship between age and the
speed limit. A scatter plot is the most ideal plot that helps visualize the relationship between two
variables. The plot can tell whether there is positive relationship between two variables or even
negative relationship or no relationship between the variables. From the figure below, we can see
that there seems to be no relationship between age of the person and the speed limit.
plot(Speed.Limit~Age,
xlab="Age", ylab="Speed
Limit",
main="Scatter plot of
Speed limit vs age")

Figure 3: A scatter plot of speed limit versus age
3.2.2 Two-variable analysis 1
The R code used for this section is given below;
In this section, we present the relationship between Crash type
and gender. The bar chart below shows the relationship between
the two variables. As can be seen, for the males, the highest type
of crash was single crash while for the females the most common
type of crash was found to be the multiple crash.
counts <- table(Crash.Type,
Gender)
counts
barplot(counts, main="Crash
Type Distribution by
Gender", ylab = "Gender",
cex.lab = 1.5, cex.main =
1.4, beside=TRUE,
col=c("darkblue","red",
"green"))
legend("topleft",
c("Multiple","Pedestrian","Si
ngle"), cex=0.5, bty="n",
fill=c("darkblue","red",
"green"))
print(chisq.test(counts))

Figure 4: Bar chart of crash type by gender
A chi-square test of association was performed to test the association between the two variables.
The hypothesis tested is;
Null hypothesis (H0): There is no association between the two variables (crash type and gender)
Alternative hypothesis (HA): There is association between the two variables (crash type and
gender)
The results of the Chi-square test are presented below;
From the table above, we can see that the p-value is 0.000 (a
value less than 5% level of significance), we therefore reject the null hypothesis and conclude
that there is significant association between the two variables (crash type and gender).
>
print(chisq.test(counts))
Pearson's Chi-
squared test
data: counts
X-squared = 79.919, df =
2, p-value < 2.2e-16

4. Advanced analysis
4.1Clustering
4.1.1 Brief explanation of k-means and clustering
Clustering means grouping objects that are similar together into what is known as a
cluster (Filipovych, et al., 2011). Cluster analysis is a commonly used technique in
statistics as well in machine learning (Frey & Dueck, 2017). It is an exploratory analysis
meant to understand how the data is similar or dissimilar (Meilă, 2013).
4.1.2 Clustering Analysis
The R code for this section is given as;
mydata <- na.omit(fatalities)
mydata <- scale(fatalities)
fit <- kmeans(mydata, 3)

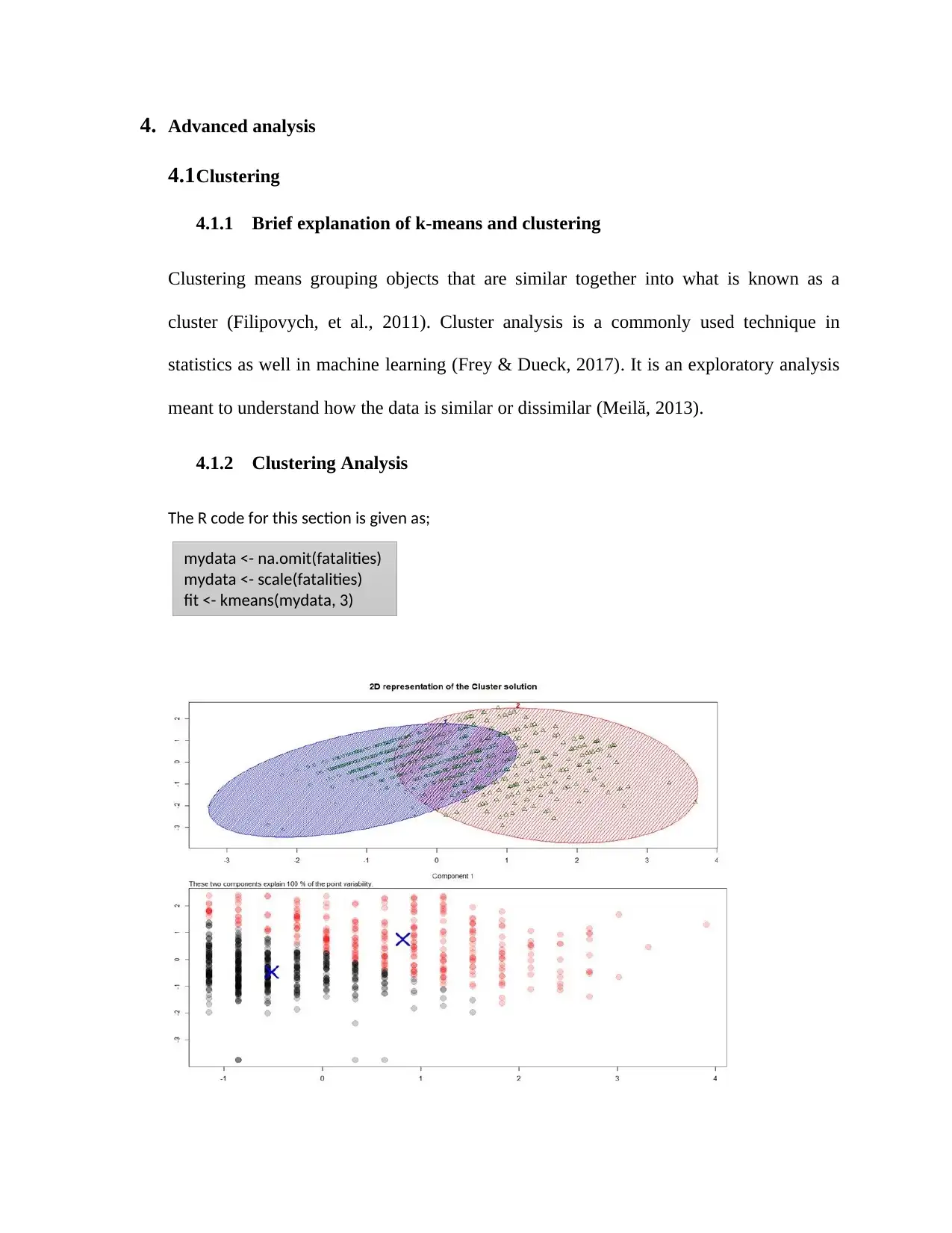
Cluster analysis showed that there is relationship between speed limit and the states as
well as territories. The data is grouped into three clusters (which includes the states and
territories).
4.2 Linear regression
4.2.1 Brief definition of linear regression
Linear regression refers to a statistical technique that helps identify the relationship
between the dependent variable and one or more independent variables (Tofallis,
2009). Simple linear regression involves one independent variable while multiple
regression involves more than one independent variable (Aldrich, 2015). This
technique (linear regression) is helpful in predicting the dependent variable. One can
estimate a linear model that can help predict and forecast the dependent variable
using the independent variables. The simple linear regression equation is of the form;

Y = β0 +β1 X
Where Y is the dependent variable, β0 is the constant (intercept) coefficient, β1 is the
coefficient of X and last X is the independent variable.
4.2.2 Linear Regression 1
The R code for this section is given as follows;
The results of the analysis is presented below;
From the above analysis, it can be seen that the
overall model is significant and that the model
is appropriate and fit to predict the speed limit using
gender [F(1, 1021) = 21.52, p = .000]. The value of
R-squared was found to be 0.0015; this suggests that
only 0.15% of the variation in the dependent
Fit1<-
lm(Speed.Limit~Gender)
summary(fit1)
> fit1<-
lm(Speed.Limit~Gender)
> summary(fit1)
Call:
lm(formula = Speed.Limit
~ Gender)
Residuals:
Min 1Q Median 3Q
Max
-67.66 -22.66 -2.66
17.34 47.34
Coefficients:
Estimate Std.
Error t value Pr(>|t|)
(Intercept) 84.4980
0.3911 216.037 < 2e-16
***
GenderMale -1.8376
0.4593 -4.001 6.34e-05
***
---
Signif. codes: 0 ‘***’
0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’
0.1 ‘ ’ 1
Residual standard error:
21.52 on 11021 degrees
of freedom
Multiple R-squared:
0.001451,
Adjusted R-
squared: 0.00136
F-statistic: 16.01 on 1
and 11021 DF, p-value:
6.343e-05

variable (speed limit) is explained by the dummy variable on gender. The dummy
variable gender was found to be significant in the model (p < 0.05).
The coefficient of the dummy variable gender (male = 1) was found to be -1.84; this
means that male drivers are expected to have a lower speed limit of about 1.84 as
compared to the female driver involved in fatalities.
The constant (intercept) coefficient was found to be 84.50. This suggests that holding the
dummy variable on gender constant, we would expect the speed limit to be 84.50.
The final regression equation model is given as;
Y =84.50−1.84 X
Where Y is the dependent variable (Speed Limit) and X is the independent variable
(dummy variable on gender).
Regression plots

4.2.3 Linear Regression 2
The R code for this section is given as follows;
The results of the analysis is presented below
Fit2<-lm(Speed.Limit~Age)
summary(fit2)
> fit2<-
lm(Speed.Limit~Age)
> summary(fit2)
Call:
lm(formula = Speed.Limit
~ Age)
Residuals:
Min 1Q Median
3Q Max
-65.219 -21.736 0.503
17.518 50.337
Coefficients:
Estimate Std.
Error t value Pr(>|t|)
(Intercept) 86.794781
0.454019 191.170 <2e-
16 ***
Age -0.082930
0.009263 -8.953 <2e-
16 ***
---
Signif. codes: 0 ‘***’
0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’
0.1 ‘ ’ 1
Residual standard error:

From the above analysis, it can be seen that the overall model is significant and that the
model is appropriate and fit to predict the speed limit using gender [F(1, 1021) = 21.46, p
= .000]. The value of R-squared was found to be 0.0072; this suggests that only 0.72% of
the variation in the dependent variable (speed limit) is explained by the independent
variable (age). The independent variable age was found to be significant in the model (p
< 0.05).
The coefficient of the independent variable age was found to be -0.0829; this means that
a unit increase in age is expected to result in a lower speed limit by 0.0829. Similarly, a
unit decrease in age is expected to result in a higher speed limit by 0.0829.
The constant (intercept) coefficient was found to be 86.79. This suggests that holding the
independent variable age constant, we would expect the speed limit to be 86.79.
The final regression equation model is given as;
Y =86.79−0.0829 X
Where Y is the dependent variable (Speed Limit) and X is the independent variable (age).
5. Conclusion
This report utilized various techniques to analyze the trends in the fatalities in Australia.
Using one variable analysis on a boxplot, an average speed limit of speed limit was found to
be 83.17 with the median speed being 80.00 while the highest and the lowest speeds were
130.00 and 15.00 respectively. Histogram showed that majority of people involved in
fatalities were young people aged between 15-25 years of age. Utilizing two variable analysis
found significant association between crash type and gender. However, there was no

relationship between speed limit and age. A simple linear regression analysis showed that
gender significantly predicts the speed limit where the males are likely to have lower speed
limit as compared to the females.
6. Reflection
This was an interesting research study and it involves utilization of various skills learnt in
class including pre-processing data and well as data cleaning, modeling and visualization.
The most crucial part of the work was cleaning the data so that a clean and ready to use data
is made available.
References
Aldrich, J., 2015. Fisher and Regression. Statistical Science, 20(4), p. 401–417.
Filipovych, R., Resnick, S. M. & Davatzikos, C., 2011. Semi-supervised Cluster Analysis of
Imaging Data. Journal of Neuro Image, 54(3), p. 2185–2197.

Frey, B. J. & Dueck, D., 2017. Clustering by Passing Messages Between Data Points. Journal of
Science, 315 (5814), p. 972–976.
Meilă, M., 2013. Comparing Clusterings by the Variation of Information: Learning Theory and
Kernel Machines. Lecture Notes in Computer Science, Volume 2777, p. 173–187.
Tofallis, C., 2009. Least Squares Percentage Regression. Journal of Modern Applied Statistical
Methods, 7(5), p. 526–534.
Appendix
R codes
fatalities<-read.csv("C:\\Users\\310187796\\Documents\\fatalities.csv")
str(fatalities)
attach(fatalities)
install.packages("cluster")
library(cluster)
summary(Speed.Limit)

boxplot(Speed.Limit, ylab="Speed Limit",
main="Boxplot of Speed Limit", col="aquamarine")
summary(Age)
hist(Age, xlab="Age", ylab="Frequency",
main="Histogram of Age", col="blanchedalmond")
plot(Speed.Limit~Age, xlab="Age", ylab="Speed Limit",
main="Scatter plot of Speed limit vs age")
library(dplyr)
new<-fatalities[!grepl("Unspecified", fatalities$Gender),]
new<-new[!grepl("-9", new$Gender),]
attach(new)
counts <- table(Crash.Type, Gender)
counts
barplot(counts, main="Crash Type Distribution by Gender", ylab = "Gender",
cex.lab = 1.5, cex.main = 1.4, beside=TRUE, col=c("darkblue","red", "green"))
legend("topleft", c("Multiple","Pedestrian","Single"), cex=0.5, bty="n", fill=c("darkblue","red",
"green"))
print(chisq.test(counts))
mydata <- na.omit(fatalities)
mydata <- scale(fatalities)
fit <- kmeans(mydata, 5)
fit1<-lm(Speed.Limit~Gender)
summary(fit1)
fit2<-lm(Speed.Limit~Age)
summary(fit2)
fit2<-lm(Speed.Limit~Easter.Period)
summary(fit2)