STA2300 Data Analysis Assignment Solution: Cardiac Arrest Patients
VerifiedAdded on 2023/03/23
|16
|1914
|22
Homework Assignment
AI Summary
This document presents a comprehensive solution to a data analysis assignment likely from a university course, focusing on statistical analysis of medical data. The assignment analyzes data related to critically ill patients who survived cardiac arrest. It covers a range of statistical techniques, including calculating confidence intervals, performing hypothesis tests (both one-tailed and two-tailed), and interpreting p-values. The solution addresses questions on heart rate, the proportion of patients who survive cardiac arrest, and risk factors associated with lung disease. The analysis utilizes t-tests, z-tests, and non-parametric tests like the Mann-Whitney test. The assignment also involves interpreting SPSS output, comparing distributions, and making conclusions based on the statistical findings. The solution includes calculations, interpretations, and conclusions for each question, ensuring a thorough understanding of the data analysis process. The assignment assesses the student's ability to apply statistical methods to real-world medical scenarios and draw meaningful insights from the data.

DATA ANALYSIS
STUDENT ID:
[Pick the date]
STUDENT ID:
[Pick the date]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question 1
(a) Population mean of heart rate of critically ill patients survived cardiac arrest = 104.97
98% confidence interval =?
Mean = 104.97
Standard deviation = 29.441
Sample size = 88 (Survival 1)
Standard error =29.441/ sqrt (88) = 3.138
Degree of freedom = 88-1 = 87
The t value for 98% confidence interval = 2.369
It is noteworthy that t value has been used since the population standard deviation is
unknown.
Margin of error = t value * standard error = 3.138 = 7.4339
Lower limit = Mean – Margin of error = 104.97 - 7.4339 = 97.53
Upper limit = Mean + Margin of error =104.97 + 7.4339 = 112.4
98% confidence interval = [97.53 112.4]
(b) Normal probability plot heart rate of critically ill patients survived cardiac arrest
2
(a) Population mean of heart rate of critically ill patients survived cardiac arrest = 104.97
98% confidence interval =?
Mean = 104.97
Standard deviation = 29.441
Sample size = 88 (Survival 1)
Standard error =29.441/ sqrt (88) = 3.138
Degree of freedom = 88-1 = 87
The t value for 98% confidence interval = 2.369
It is noteworthy that t value has been used since the population standard deviation is
unknown.
Margin of error = t value * standard error = 3.138 = 7.4339
Lower limit = Mean – Margin of error = 104.97 - 7.4339 = 97.53
Upper limit = Mean + Margin of error =104.97 + 7.4339 = 112.4
98% confidence interval = [97.53 112.4]
(b) Normal probability plot heart rate of critically ill patients survived cardiac arrest
2

3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Based on the above plots, it is apparent that the underlying variable of interest can be
assumed to be normally distributed.
(c) Null and alternative hypotheses
H0: μ <= 90 i.e. the mean heart rate for critically ill patients admitted to hospital in cardiac
arrest who survived is not higher than that of the overall population
Ha: μ > 90 i.e. the mean heart rate for critically ill patients admitted to hospital in cardiac
arrest who survived is higher than that of the overall population
(d) The test statistics computation is shown below.
t stat = (Sample mean – Hypothesised mean)/Standard Error
t stat= 104.97−90
3.138
t stat=4.77
(e) The p value computation is shown below.
Sample size = 88 (Survival 1)
Degree of freedom = 88-1 = 87
The p value = 0.00001 (based on relevant tables and df)
Significance level = 0.01
It can be seen that the p value is lower than the significance level and hence, sufficient
evidence is present to reject the null hypothesis and to accept the alternative hypothesis.
Therefore, it can be concluded that the average heart rate of adults is more than 90 beats per
minutes. Hence, it would be correct to conclude that the mean heart rate for critically ill
patients admitted to hospital in cardiac arrest who survived is higher than that of the overall
population.
4
assumed to be normally distributed.
(c) Null and alternative hypotheses
H0: μ <= 90 i.e. the mean heart rate for critically ill patients admitted to hospital in cardiac
arrest who survived is not higher than that of the overall population
Ha: μ > 90 i.e. the mean heart rate for critically ill patients admitted to hospital in cardiac
arrest who survived is higher than that of the overall population
(d) The test statistics computation is shown below.
t stat = (Sample mean – Hypothesised mean)/Standard Error
t stat= 104.97−90
3.138
t stat=4.77
(e) The p value computation is shown below.
Sample size = 88 (Survival 1)
Degree of freedom = 88-1 = 87
The p value = 0.00001 (based on relevant tables and df)
Significance level = 0.01
It can be seen that the p value is lower than the significance level and hence, sufficient
evidence is present to reject the null hypothesis and to accept the alternative hypothesis.
Therefore, it can be concluded that the average heart rate of adults is more than 90 beats per
minutes. Hence, it would be correct to conclude that the mean heart rate for critically ill
patients admitted to hospital in cardiac arrest who survived is higher than that of the overall
population.
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

(f) SPSS output of hypothesis testing is shown below.
The sample statistic comes out to be same. However, a major difference is that the above
output from SPSS has been derived considering the test is two tail while in actually the test is
right tail and single tail test. Also, the SPSS output also indicates the 95% confidence
interval.
Question 2
(a) The variable of interest to the researcher is the proportion of all critically ill patients
admitted to hospital in cardiac arrest who survived.
(b) Null and alternative hypothesis
H0: p = 0.55 i.e. proportion of critically ill patients admitted to hospital in cardiac arrest
survive is not significantly different from 0.55.
Ha: p ≠ 0.55 i.e. proportion of critically ill patients admitted to hospital in cardiac arrest
survive is significantly different from 0.55.
(c) In the given case, the binomial has been approximated as normal distribution. The
necessary conditions for the same are as follows.
np≥ 10
npq≥10
Here, n = 88, p =0.603, q = (1-0.0603)
5
The sample statistic comes out to be same. However, a major difference is that the above
output from SPSS has been derived considering the test is two tail while in actually the test is
right tail and single tail test. Also, the SPSS output also indicates the 95% confidence
interval.
Question 2
(a) The variable of interest to the researcher is the proportion of all critically ill patients
admitted to hospital in cardiac arrest who survived.
(b) Null and alternative hypothesis
H0: p = 0.55 i.e. proportion of critically ill patients admitted to hospital in cardiac arrest
survive is not significantly different from 0.55.
Ha: p ≠ 0.55 i.e. proportion of critically ill patients admitted to hospital in cardiac arrest
survive is significantly different from 0.55.
(c) In the given case, the binomial has been approximated as normal distribution. The
necessary conditions for the same are as follows.
np≥ 10
npq≥10
Here, n = 88, p =0.603, q = (1-0.0603)
5

The above conditions are satisfied and hence it is fair to assume that the given binomial
distribution can be approximated to normal distribution.
(d) Test statistics can be computed using the following formula.
z= p∗−p
√ p(1−p)
n
z=test statistis
p∗¿Observed proportion=0.603
p=Hypothesized value=0.55
n=sample ¿ 146
z= p∗− p
√ p ( 1− p )
n
= 0.603−0.55
√ 0.55 ( 1−0.55 )
146
z=1.287
(e) It is a two tailed hypothesis test and thus, the p value = 0.1981
It can be seen that the p value (0.1981) is higher than the significance level (0.01) and hence,
insufficient evidence is present to reject the null hypothesis and to accept the alternative
hypothesis. Therefore, it can be concluded that the proportion of critically ill patients
admitted to hospital in cardiac arrest survive does not significantly vary from 0.55.
(f) Margin of error = 0.02
6
distribution can be approximated to normal distribution.
(d) Test statistics can be computed using the following formula.
z= p∗−p
√ p(1−p)
n
z=test statistis
p∗¿Observed proportion=0.603
p=Hypothesized value=0.55
n=sample ¿ 146
z= p∗− p
√ p ( 1− p )
n
= 0.603−0.55
√ 0.55 ( 1−0.55 )
146
z=1.287
(e) It is a two tailed hypothesis test and thus, the p value = 0.1981
It can be seen that the p value (0.1981) is higher than the significance level (0.01) and hence,
insufficient evidence is present to reject the null hypothesis and to accept the alternative
hypothesis. Therefore, it can be concluded that the proportion of critically ill patients
admitted to hospital in cardiac arrest survive does not significantly vary from 0.55.
(f) Margin of error = 0.02
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

True proportion of critically ill patients admitted to hospital in cardiac arrest survive = 0.55
The z value for 99% confidence interval = 2.58
Minimum sample size (n) =?
n=( z
Margin of error )
2
∗p ( 1−p ) = ( 2.58
0.02 )
2
∗0.5∗(1−0.5)=4161
(g) Margin of error = 0.02
True proportion of critically ill patients admitted to hospital in cardiac arrest survive = 0.603
The z value for 99% confidence interval = 2.58
Minimum sample size =?
z∗¿ ( z
Margin of error )2
∗p ( 1− p ) =( 2.58
0.02 )2
∗0.603∗(1−0.603)=3984
Hence, impact of the decision is to lower the minimum sample size required.
Question 3
(a) Null and alternative hypothesis
H0: μ (side stream) = μ(main stream) i.e. the risk of lung disease is not significant different
for non-smokers who tend to live with smokers
Ha: μ(side stream) > μ(main stream) i.e. the risk of lung disease is higher for non- smokers
who tend to live with smokers
(b) The various assumptions accompanying the given test are indicated below.
The sample data has been collected through random sampling from the population of
interest.
Both the variables should be approximately normal in their underlying distribution.
Also, the sample size should be reasonably large.
7
The z value for 99% confidence interval = 2.58
Minimum sample size (n) =?
n=( z
Margin of error )
2
∗p ( 1−p ) = ( 2.58
0.02 )
2
∗0.5∗(1−0.5)=4161
(g) Margin of error = 0.02
True proportion of critically ill patients admitted to hospital in cardiac arrest survive = 0.603
The z value for 99% confidence interval = 2.58
Minimum sample size =?
z∗¿ ( z
Margin of error )2
∗p ( 1− p ) =( 2.58
0.02 )2
∗0.603∗(1−0.603)=3984
Hence, impact of the decision is to lower the minimum sample size required.
Question 3
(a) Null and alternative hypothesis
H0: μ (side stream) = μ(main stream) i.e. the risk of lung disease is not significant different
for non-smokers who tend to live with smokers
Ha: μ(side stream) > μ(main stream) i.e. the risk of lung disease is higher for non- smokers
who tend to live with smokers
(b) The various assumptions accompanying the given test are indicated below.
The sample data has been collected through random sampling from the population of
interest.
Both the variables should be approximately normal in their underlying distribution.
Also, the sample size should be reasonably large.
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

(c) The test statistics computation is shown below.
8
8

The test statistics t = 2.61
(d) The p value
Degree of freedom = 7+7-2 = 12
The right tailed p value = 0.0115
Significance level = 0.01
(e) It can be seen that the p value (0.0115) is higher than the significance level (0.01) and
hence, insufficient evidence is present to reject the null hypothesis and to accept the
alternative hypothesis. Therefore, it can be concluded that the mean yield of side stream is
not higher than the mean yield of main stream.
(f) The relevant non-parametric test is Mann Whitney Test. This has been conducted for the
given data and the requisite output shown below.
9
(d) The p value
Degree of freedom = 7+7-2 = 12
The right tailed p value = 0.0115
Significance level = 0.01
(e) It can be seen that the p value (0.0115) is higher than the significance level (0.01) and
hence, insufficient evidence is present to reject the null hypothesis and to accept the
alternative hypothesis. Therefore, it can be concluded that the mean yield of side stream is
not higher than the mean yield of main stream.
(f) The relevant non-parametric test is Mann Whitney Test. This has been conducted for the
given data and the requisite output shown below.
9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Considering a level of significance of 1%, the available evidence does not warrant rejection
of null hypothesis. Therefore, it can be concluded that the mean yield of side stream is not
higher than the mean yield of main stream.
10
of null hypothesis. Therefore, it can be concluded that the mean yield of side stream is not
higher than the mean yield of main stream.
10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
(g) It is apparent that the p value is different in the two tests which even though lead to the
same conclusion but could potentially have been different. Also, the test statistic is
different for the two tests. This may be attributed to difference in approach.
Question 4
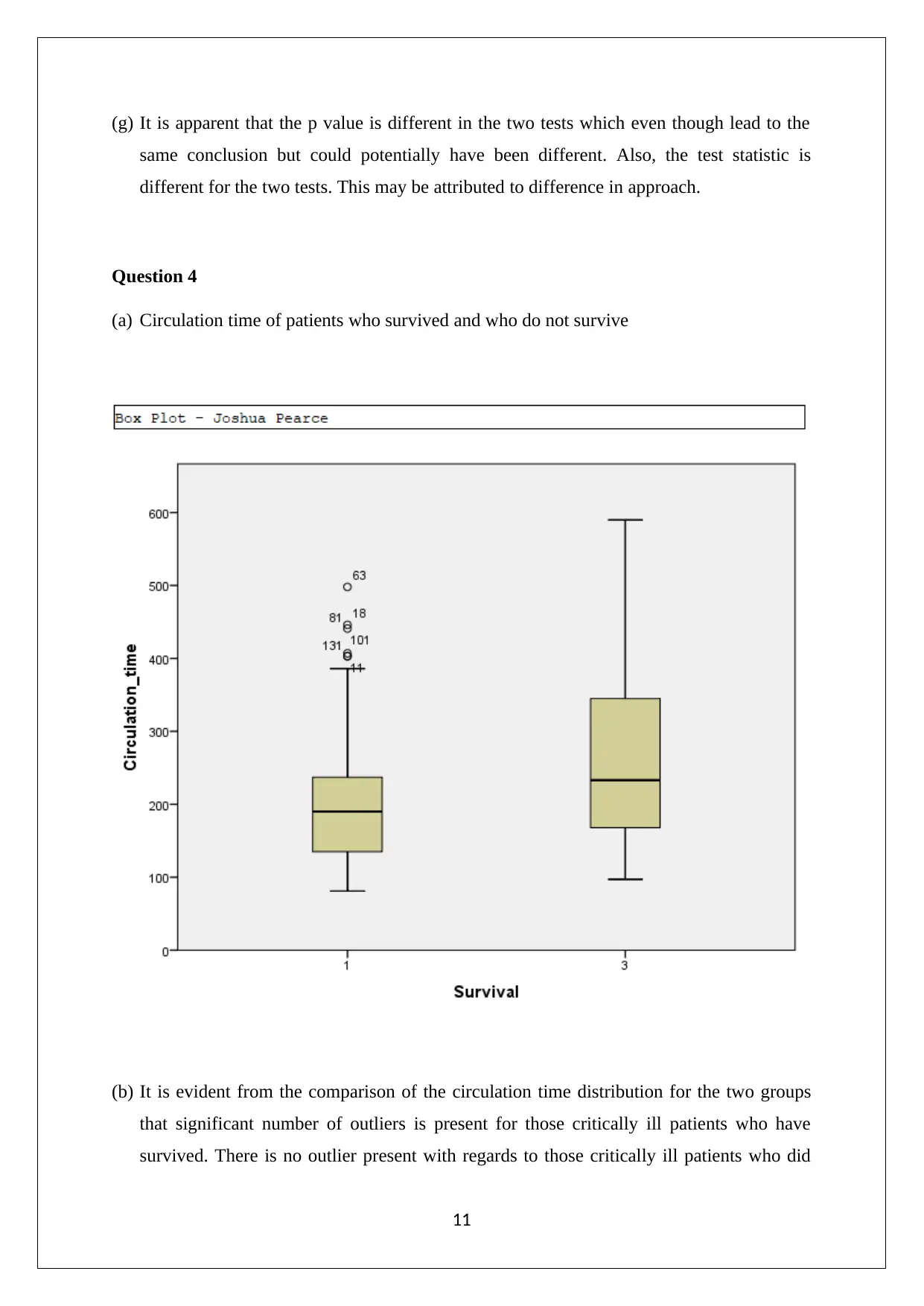
(a) Circulation time of patients who survived and who do not survive
(b) It is evident from the comparison of the circulation time distribution for the two groups
that significant number of outliers is present for those critically ill patients who have
survived. There is no outlier present with regards to those critically ill patients who did
11
same conclusion but could potentially have been different. Also, the test statistic is
different for the two tests. This may be attributed to difference in approach.
Question 4
(a) Circulation time of patients who survived and who do not survive
(b) It is evident from the comparison of the circulation time distribution for the two groups
that significant number of outliers is present for those critically ill patients who have
survived. There is no outlier present with regards to those critically ill patients who did
11

not survive. The shape of both the groups is skewed on the upper end. With regards to the
centre, comparison of median values is appropriate. This has been done which highlights
that higher circulation time on average is observed for critically ill patients who do not
survive. The extent of dispersion is higher for those patient group who did not survive.
(c) Null and alternative hypothesis
H0: μ (circulation time survived) >= μ (circulation time not survived) i.e. it take more or
equal time, on average, for the blood to pump around the body for those who survive cardiac
arrest compared with those who ultimately do not survive
Ha: μ (circulation timesurvived) < μ (circulation time not survived) i.e. it take less time, on
average, for the blood to pump around the body for those who survive cardiac arrest
compared with those who ultimately do not survive
(d) The assumptions for the given test are not satisfied considering that survival group
comprises of a host of outliers which implies high extent of skew. Also, the group
indicating people who died has a right skew implying non-normality.
(e) The test statistics is computed below.
12
centre, comparison of median values is appropriate. This has been done which highlights
that higher circulation time on average is observed for critically ill patients who do not
survive. The extent of dispersion is higher for those patient group who did not survive.
(c) Null and alternative hypothesis
H0: μ (circulation time survived) >= μ (circulation time not survived) i.e. it take more or
equal time, on average, for the blood to pump around the body for those who survive cardiac
arrest compared with those who ultimately do not survive
Ha: μ (circulation timesurvived) < μ (circulation time not survived) i.e. it take less time, on
average, for the blood to pump around the body for those who survive cardiac arrest
compared with those who ultimately do not survive
(d) The assumptions for the given test are not satisfied considering that survival group
comprises of a host of outliers which implies high extent of skew. Also, the group
indicating people who died has a right skew implying non-normality.
(e) The test statistics is computed below.
12
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 16
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


