Data Analysis: Frequency Table, Histogram, Regression Model and Hypothesis Testing
Prepare a frequency distribution, relative frequency distribution, and percent frequency
4 Pages550 Words85 Views
Added on 2023-06-11
About This Document
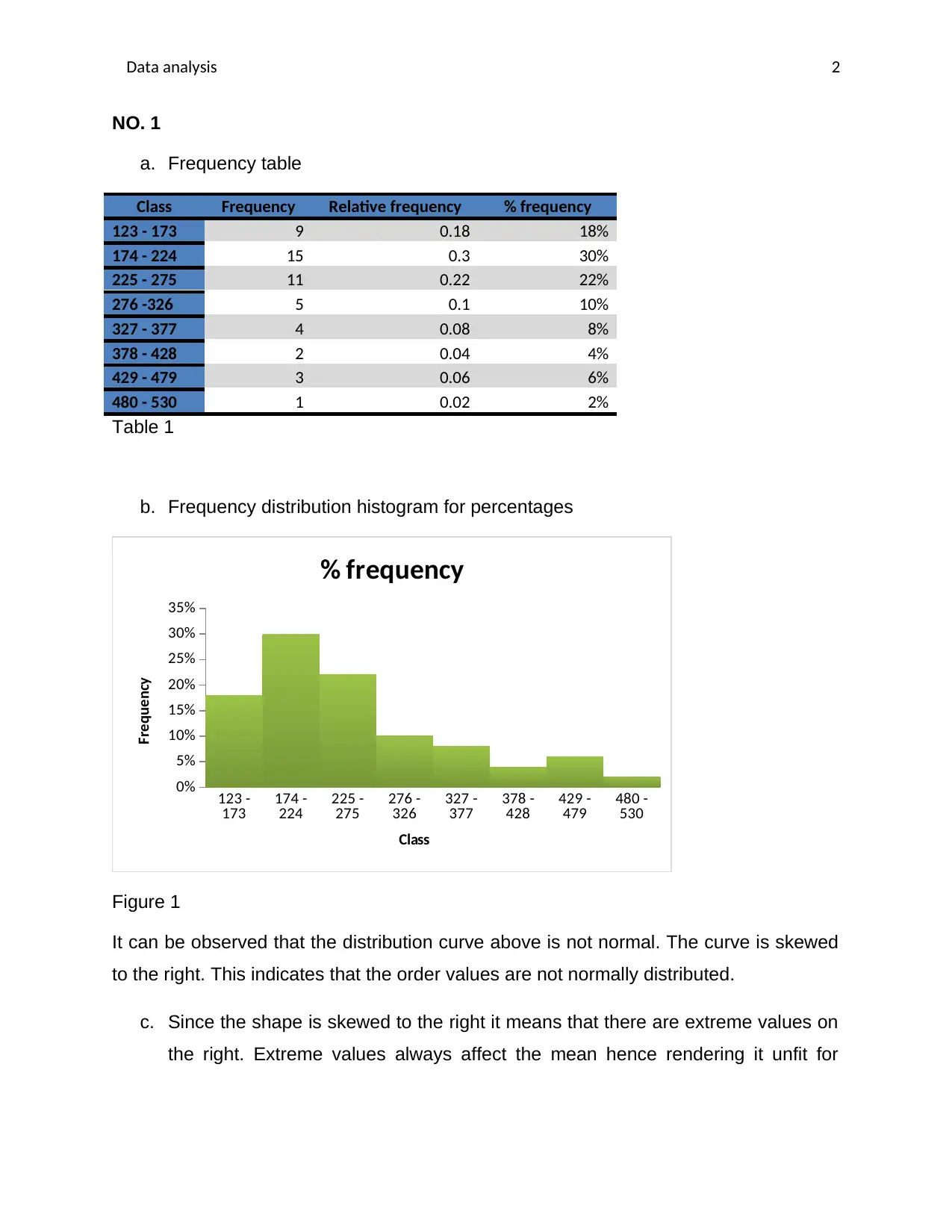
This article covers data analysis techniques such as frequency table, histogram, regression model and hypothesis testing with examples and interpretations.
No documents found. Try with a different documents.
Data Analysis: Frequency Tables, Regression Analysis, Hypothesis Testing
|4
|549
|225
Data Analysis: Frequency Table, Histogram, Regression Analysis, Hypothesis Testing
|4
|527
|497
Data Analysis: Frequency Distribution, Regression Analysis, Hypothesis Testing
|4
|544
|385
Statistics - Assignment (Solution)
|7
|703
|137
HI6007 - Statistics And Research Methods For Business
|6
|758
|136