Data Representation and Digital Logic Assignment 1

This assignment covers topics like one's complement, two's complement, signed magnitude, unsigned magnitude, binary, octal, decimal, hexadecimal, Boolean functions, and circuit diagrams.

Student Name: Kwame Kyei Ampofo Agyapong
Student ID: 11615762
Subject Code: ITC544
Assignment 1: Data Representation and Digital Logic
Page 1 of 12

Contents
Question 1..................................................................................................................................3
Part (a)....................................................................................................................................3
Part (b)....................................................................................................................................4
Question 2..................................................................................................................................8
Part (a)....................................................................................................................................8
Part (b)....................................................................................................................................9
Appendix..................................................................................................................................11
List of Figures
Figure 1- Circuit Diagram of the Boolean function.................................................................10
Page 2 of 12

Question 1
Part (a)
As the word size is given as 8 bits, therefore, n=8 can be taken.
(I) For One’s complement
The general representation range of 1’s complement is [− ( 2n−1−1 ) ; ( 2n−1−1 ) ]
Therefore, the range of 1’s complement is going to be:
=[ − ( 28−1−1 ) ; ( 28−1−1 ) ]
= [-127; 127]
After that converting them into binary I get,
10000000 to 11111111 which represents -127 to -0.
(II) For two’s complement
The general representation range of the 2’s complement is [− ( 2n−1 ) ; ( 2n−1−1 ) ]
Therefore, the range of 2’s complement is going to be:
= [− ( 28−1 ) ; ( 28 −1−1 ) ]
= [-128; 127]
Now on converting the range into the binary equivalent I get,
10000000 to 11111111 which is going to represent -128 to -1.
(III) For signed magnitude
The general representation range is -2(n-1) to +2(n-1)
On substituting the n=8 I get,
= -2(8-1) to +2(8-1)
= -128 to 128
On converting the rage into decimal equivalent I get,
00000000 to 01111111 which is going to represent 0 to 127.
(III) For the unsigned magnitude
The range is going to be 10000000 to 11111111.
It is going to represent 128 to 255.
Page 3 of 12

Part (b)
I. 0x5AB into Octal
As 0x represents the Hexadecimal number. So the conversion of the hexadecimal to the octal
number is going to be as follow:
Firstly, I am going to convert the hexadecimal number to the decimal equivalent. For that
certain equation is required which is shown below:
= 5*162 +10*161 +11*160
=1280+160+11
= (1451)10
Now to convert into the octal certain procedures has to be followed which is shown below:
8 1451
8 181 3
8 22 5
2 6
So the octal number is (2653)8 or it can be represented as 0o2653.
II. 101101.1012 into Decimal
For that I have to follow certain steps which is shown below:
=1*25+ 0*24+ 1*22+ 0*21+ 1*20
= 32 + 0 + 8 + 4 + 0 + 1
= 45
Now, for decimal part i.e. 101,
I have done certain calculation which is shown below:
= 1*2-1 + 0*2-2 +1*2-3
= 0.5 + 0 + 0.125
= 0.625
On combining both part, solution is going to be:
= (45.625)10
III. 12348 into Binary
To perform this conversion, I have to convert this into decimal. For that certain steps have to
be followed which are shown below:
= 1*83+ 2*82+ 3*81+ 4*80
= 512+ 128 + 24 + 4
Page 4 of 12

= (668)10
Now I need to convert into the binary equivalent which is shown below:
2 668
2 334 0
2 167 0
2 83 1
2 41 1
2 20 1
2 10 0
2 5 0
2 2 1
2 1 0
So the equivalent number is going to be (1010011100)2
IV. 679810 into Base 5 number
5 6798
5 1359 3
5 271 4
5 54 1
5 10 4
5 2 0
So the equivalent number is going to be (204143)5
V. 976.6310 into Binary
Firstly, converting 976 into the base 10,
2 976
2 488 0
2 244 0
2 122 0
2 61 0
2 30 1
2 15 0
2 7 1
2 3 1
2 1 1
Now converting .63 into the binary equivalent. For that certain procedure has to be followed
which is shown below:
=0.63*2
0.63*2= 1.26 1
0.26*2= 0.52 0
0.52*2= 1.04 1
.04*2= 0.08 0
On combining,
(1111010000.101)2
Page 5 of 12

Page 6 of 12

VI. 1001001011 into Hexadecimal
By taking the help of the table which is shown below:
Conversion is going to be implemented by grouping four numbers starting from right side to
the left side. After by taking the help of table I get,
0010- 2
0100- 4
1011- B
So the desired result is going to be 24B.
VII. 10011110 (8-bit 2’s complement representation) to Decimal
On solving unsigned:
=1⋅2⁷ + 0⋅2 + 0⁶ ⋅2⁵ + 1⋅2⁴ + 1⋅2³ + 1⋅2² + 1⋅2¹ + 0⋅2⁰
=1⋅2⁷ + 1⋅2⁴ + 1⋅2³ + 1⋅2² + 1⋅2¹
=128 + 16 + 8 + 4 + 2
=158
On solving signed magnitude which is (bit 1⋅2⁷ means negative value)
= 0⋅2 + 0⁶ ⋅2⁵ + 1⋅2⁴ + 1⋅2³ + 1⋅2² + 1⋅2¹ + 0⋅2⁰
=1⋅2⁴ + 1⋅2³ + 1⋅2² + 1⋅2¹
=16 + 8 + 4 + 2
= -30 (on applying the sign)
On solving one's complement which is (bit 1⋅2⁷ means negative value, therefore I have to
complement all bits)
Step 1 = (1⋅2⁷ + 0⋅2 + 0⁶ ⋅2⁵ + 1⋅2⁴ + 1⋅2³ + 1⋅2² + 1⋅2¹ + 0⋅2 )⁰
Step 2 =0⋅2⁷ + 1⋅2 + 1⁶ ⋅2⁵ + 0⋅2⁴ + 0⋅2³ + 0⋅2² + 0⋅2¹ + 1⋅2⁰
=1⋅2 + 1⁶ ⋅2⁵ + 1⋅2⁰
Page 7 of 12

=64 + 32 + 1
= -97 (on applying the sign)
On solving Two's complement which is (bit 1⋅2⁷ means negative, complement bits, add 1)
= (1⋅2⁷ + 0⋅2 + 0⁶ ⋅2⁵ + 1⋅2⁴ + 1⋅2³ + 1⋅2² + 1⋅2¹ + 0⋅2 ) + 1⁰
= (0⋅2⁷ + 1⋅2 + 1⁶ ⋅2⁵ + 0⋅2⁴ + 0⋅2³ + 0⋅2² + 0⋅2¹ + 1⋅2 ) + 1⁰
= (1⋅2 + 1⁶ ⋅2⁵ + 1⋅2 ) + 1⁰
= (64 + 32 + 1) + 1
= -98 (on applying the sign)
Page 8 of 12

Question 2
Part (a)
According to question X’(X+Y) + (XX+Y) (Y’+X) = Y+X I need to prove this.
Taking LHS I get,
=X’(X+Y) + (XX+Y) (Y’+X)
On expanding I get,
=X’X+ X’Y+(X+Y) (Y’+X)
Since, X’X=0 therefore,
=0+X’Y+XY’+XX+YY’+YX
=0+X’Y+XY’+X+0+YX
Taking X common I get,
=X’Y + X(1+Y’) + YX
And 1+Y’=1
Therefore, the above expression becomes,
=X’Y+X+XY
Now, on adding XX’
The expression becomes,
=X’Y+X.X+XY+XX’
Taking X and Y out, the expression is going to as shown below:
=X(X’+X) + Y(X+X’)
=(X+Y) (X+X’)
Since X+X’=1
Therefore, on substituting inside the expression, it becomes,
=(X+Y) (1)
X+Y=RHS
Page 9 of 12

Part (b)
As the subject has 4 assessments, therefore the four inputs are required. I have taken four
inputs which are shown below:
A- Assignment
B- Blog
C- Discussion form
D- Quiz
As the student is going to be pass only if he passes two or more than two assessments.
So the function is going to be BC+CD+BD
Also, the student has to pass the assignment with 50 or above. And on analysing the problem,
I have taken output as Y.
So the function of the above problem is going to be:
Y=A.(BC+CD+BD)
The truth table of the above circuit is shown below:
A B C D Y
0 0 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 0
0 1 0 1 0
0 1 1 0 0
0 1 1 1 0
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 1
1 1 0 0 0
1 1 0 1 1
1 1 1 0 1
1 1 1 1 1
The minimized Boolean function can be built by taking the help of K-Map. This is shown
below:
C’D’ C’D CD CD’
A’B
’
A’B
AB 1 1 1
AB’ 1
Page 10 of 12

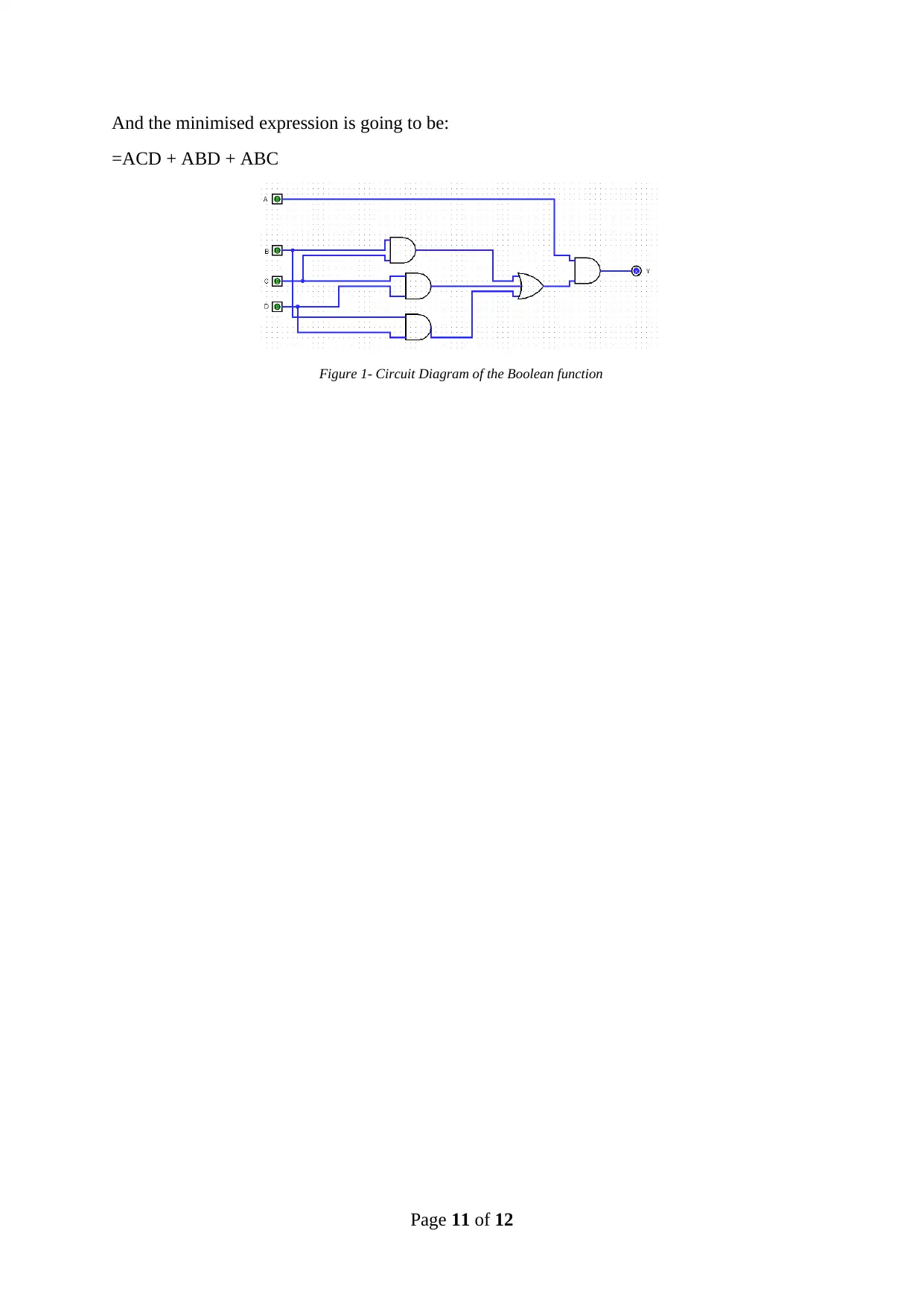
And the minimised expression is going to be:
=ACD + ABD + ABC
Figure 1- Circuit Diagram of the Boolean function
Page 11 of 12

Appendix
Page 12 of 12