ITC544 Assignment 1: In-Depth Analysis of Data Representation & Logic
VerifiedAdded on 2023/06/15
|6
|987
|84
Homework Assignment
AI Summary
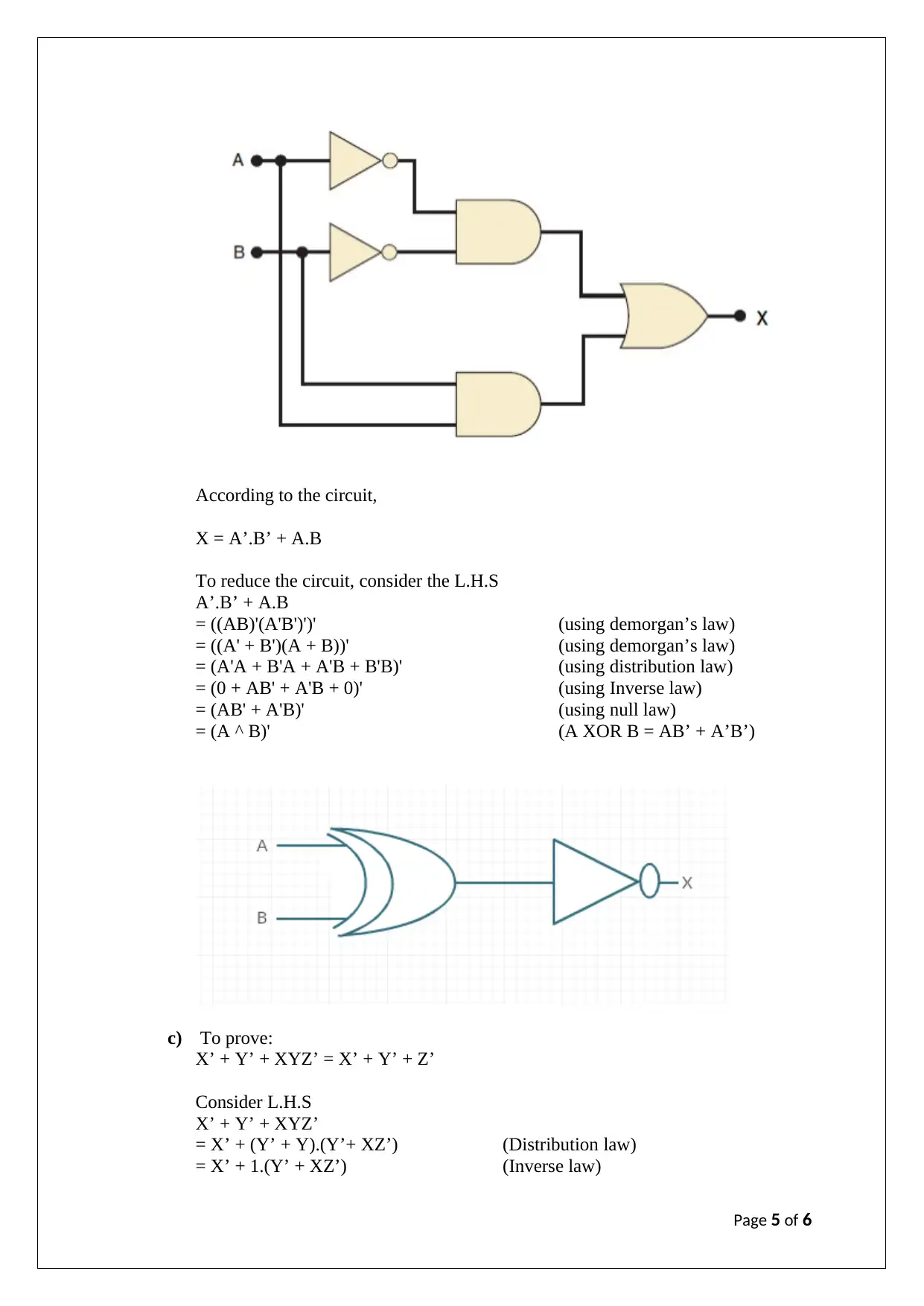
This ITC544 assignment solution delves into data representation and digital logic, addressing questions related to number system conversions and circuit simplification. The assignment begins by determining the base 'x' for a given equation involving hexadecimal and base 'x' numbers. It proceeds to convert numbers between different bases, including hexadecimal to base-3, base-7 to binary, base-5 to octal, and base-8 to decimal. Further, the document explores the representation of numbers in one's complement, two's complement, and signed magnitude formats, identifying the lowest negative and highest positive values for a 3-bit computer. The assignment also examines the equivalence of two combinational circuits using Boolean algebra and truth tables. Lastly, the document includes a question on circuit reduction using Boolean identities and laws, along with a proof involving DeMorgan's law, distribution law, and inverse law. Desklib provides a platform for students to access similar solved assignments and past papers.
1 out of 6










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)