Linear Programming Formulation and Solutions

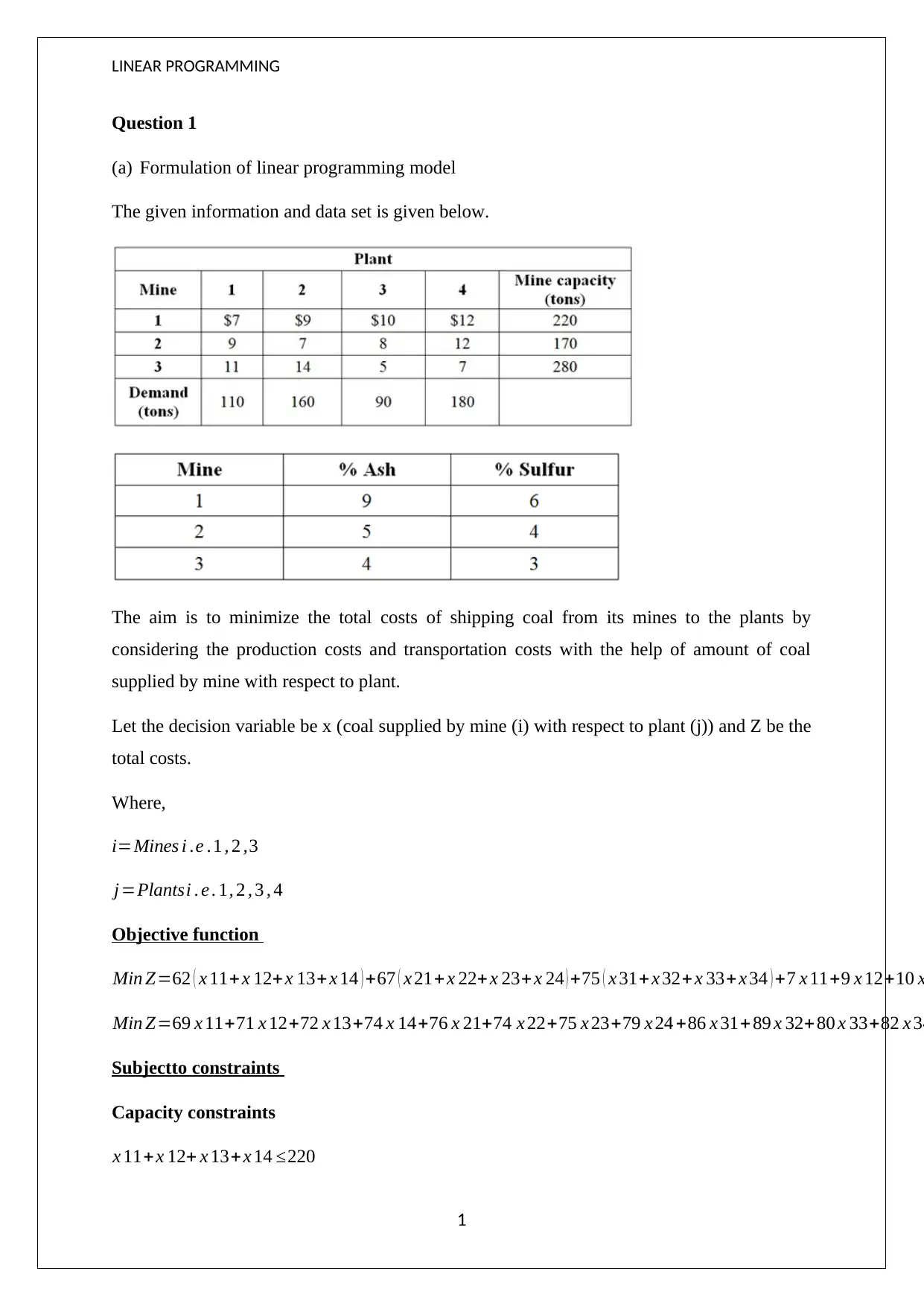
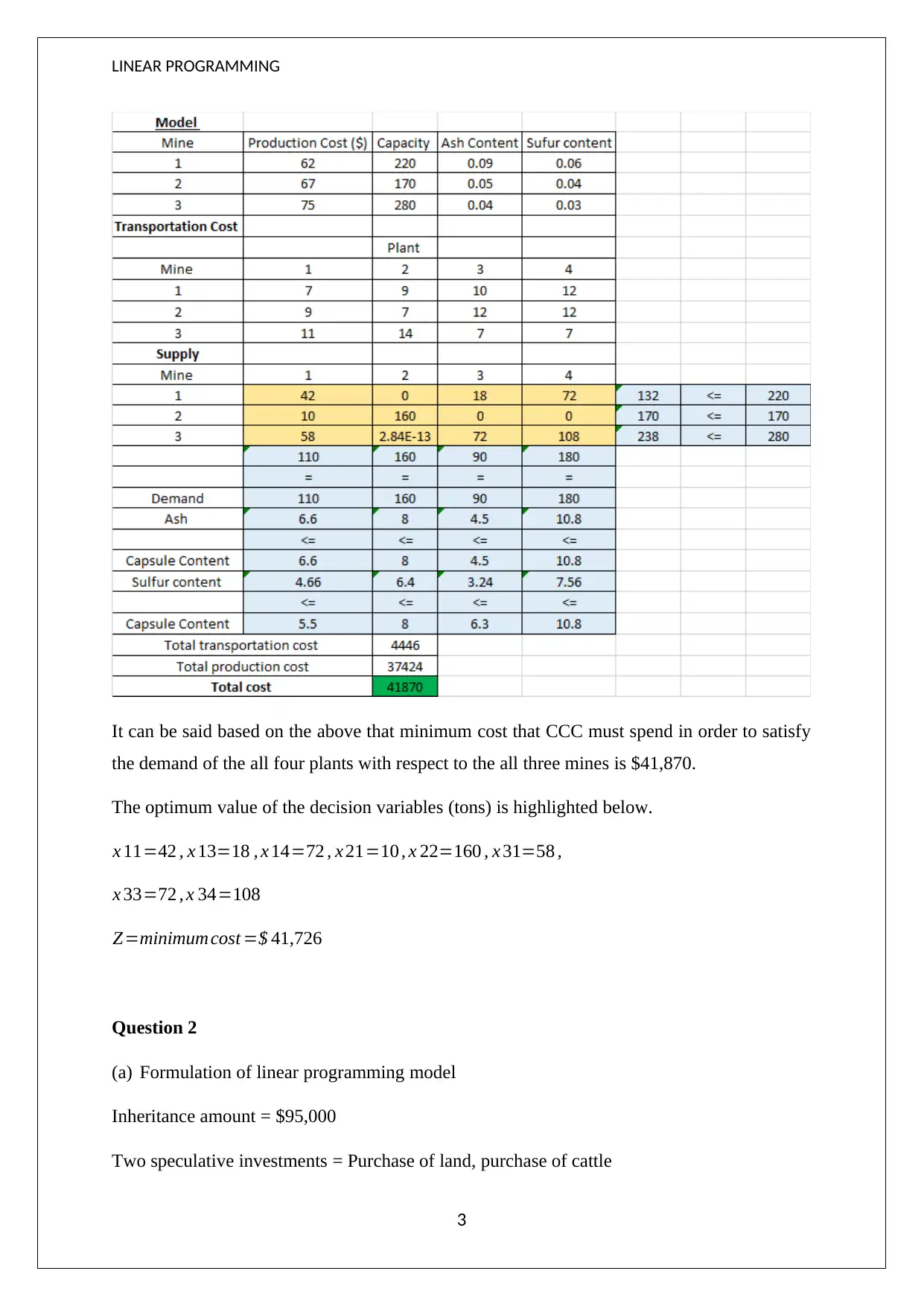
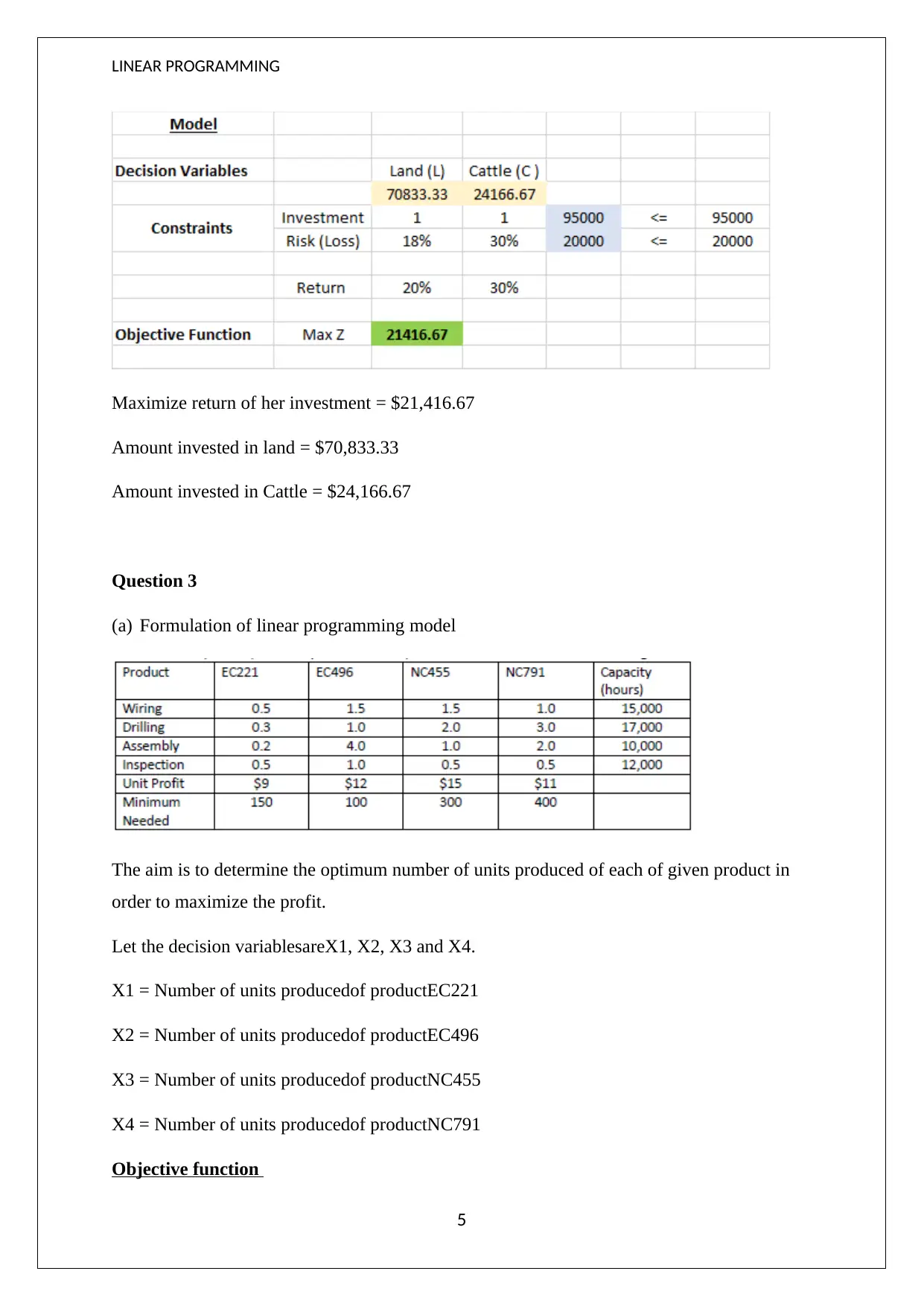
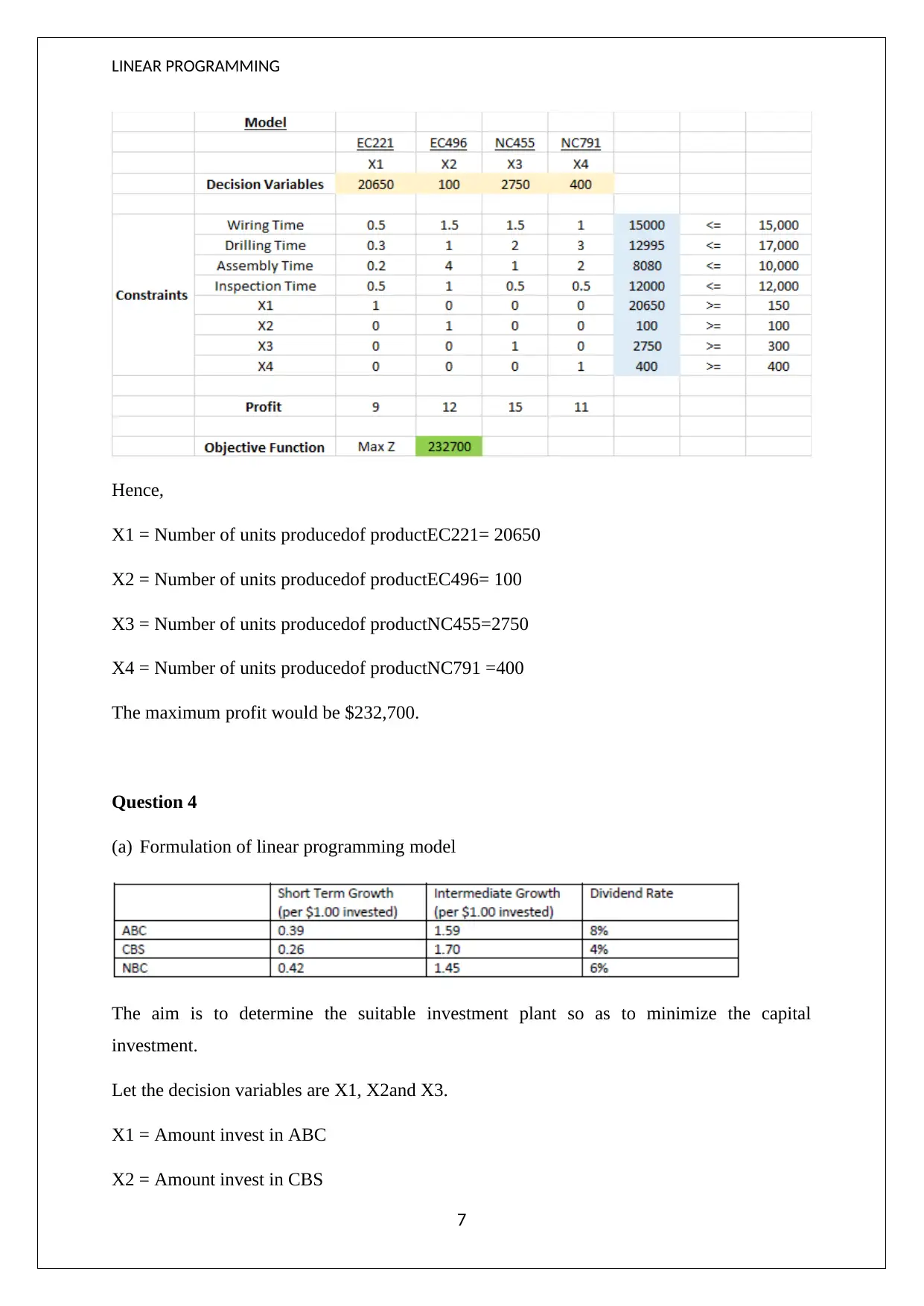
This document provides examples of linear programming problems and their solutions. It covers topics such as formulation of linear programming models, objective functions, constraints, and the use of Excel add-ins to solve these models. The examples include problems related to shipping coal, investment allocation, and production planning. The document also highlights the optimal solutions and provides insights into the decision-making process. If you need assistance with linear programming assignments or essays, Desklib is here to help.

FNCE 113 Linear Programming
[Document subtitle]
[DATE]
Grizli777
[Company address]

LINEAR PROGRAMMING
Question 1
(a) Formulation of linear programming model
The given information and data set is given below.
The aim is to minimize the total costs of shipping coal from its mines to the plants by
considering the production costs and transportation costs with the help of amount of coal
supplied by mine with respect to plant.
Let the decision variable be x (coal supplied by mine (i) with respect to plant (j)) and Z be the
total costs.
Where,
i=Mines i .e .1 , 2 ,3
j=Plantsi . e . 1, 2 , 3 , 4
Objective function
Min Z=62 ( x 11+ x 12+ x 13+ x 14 ) +67 ( x 21+x 22+ x 23+ x 24 ) +75 ( x 31+ x 32+ x 33+x 34 ) +7 x 11+9 x 12+10 x
Min Z=69 x 11+71 x 12+72 x 13+74 x 14+76 x 21+74 x 22+75 x 23+79 x 24 +86 x 31+ 89 x 32+ 80 x 33+82 x 34
Subjectto constraints
Capacity constraints
x 11+x 12+ x 13+x 14 ≤220
1

LINEAR PROGRAMMING
x 21+ x 22+x 23+ x 24 ≤170
x 31+x 32+ x 33+x 34 ≤280
Demand constraints
x 11+ x 21+ x 31=110
x 12+ x 22+ x 32=160
x 13+ x 23+x 33=90
x 12+ x 22+ x 32=180
Constraints for ash
0.09 x 11+0.05 x 21+ 0.04 x 31 ≤0.06 ( x 11+x 21+x 31 )
0.03 x 11−0.01 x 21−0.02 x 31 ≤0
0.04 x 12−0 x 22−0.01 x 32≤ 0
0.04 x 13−0 x 23−0.01 x 33 ≤ 0
0.03 x 14−0.01 x 24−0.02 x 34 ≤0
Constraints for sulphur
0.01 x 11−0.1 x 21−0.02 x 31 ≤0
0.01 x 12−0.01 x 22−0.02 x 32 ≤0
0.01 x 13−0.03 x 23−0.04 x 33 ≤ 0
0.0 x 14−0.02 x 24−0.03 x 34 ≤ 0
Non-negativity constraints; x ij ≥ 0
(b) The above highlighted linear programming model has been solved with the help of excel
add-ins ‘solver’ and the output is shown below.
2

LINEAR PROGRAMMING
It can be said based on the above that minimum cost that CCC must spend in order to satisfy
the demand of the all four plants with respect to the all three mines is $41,870.
The optimum value of the decision variables (tons) is highlighted below.
x 11=42 , x 13=18 , x 14=72 , x 21=10 , x 22=160 , x 31=58 ,
x 33=72 , x 34=108
Z=minimum cost =$ 41,726
Question 2
(a) Formulation of linear programming model
Inheritance amount = $95,000
Two speculative investments = Purchase of land, purchase of cattle
3

LINEAR PROGRAMMING
Each dollar invested in land would return the principal and 20% of principal.
Each dollar invested in cattle would return the principal and 30% of principal.
Probability of risk that she will lose the amount invested in land = 18%
Probability of risk that she will lose the amount invested in cattle = 30%
Michelle does not want to lose the amount (average) =$20,000
The aim is to determine the allocation of the investment amount between the two investment
options in order to maximize the cash value of her investment at the year 1 end.
Let the decision variable is L and C.
Where,
L= Amount invested ∈land
C= Amount invested ∈Cattle
Objective function
Max Return Z=0.20 L+0.30C
Subject to constraints
Total investment constraints
L+C ≤ 95,000
Risk constraint
0.18 L+0.30 C ≤ 20000
Non-negativity constraints; L ,C ≥0
(b) The above highlighted linear programming model has been solved by using ‘solver’ and
the output is shown below.
4

LINEAR PROGRAMMING
Maximize return of her investment = $21,416.67
Amount invested in land = $70,833.33
Amount invested in Cattle = $24,166.67
Question 3
(a) Formulation of linear programming model
The aim is to determine the optimum number of units produced of each of given product in
order to maximize the profit.
Let the decision variablesareX1, X2, X3 and X4.
X1 = Number of units producedof productEC221
X2 = Number of units producedof productEC496
X3 = Number of units producedof productNC455
X4 = Number of units producedof productNC791
Objective function
5

LINEAR PROGRAMMING
Maximize Profit Z=9 X 1+12 X 2+15 X 3+ 11 X 4
Subject to constraints
Hours of wiring availableconstraints
0.5 X 1+1.5 X 2+ 1.5 X 3+1 X 4 ≤15,000
Hours of drilling available
0.3X1 + 1X2 + 2X3 + 3X4 ≤ 17,000
Hours of assembly available
0.2X1 + 4X2 + 1X3 + 2X4 ≤ 10,000
Hours of inspection available
0.5X1 + 1X2 + 0.5X3 + 0.5X4 ≤ 12,000
X 1 ≥150
X 2 ≥100
X 3 ≥ 300
X 4 ≥ 400
Non-negativity constraints; L ,C ≥0
(b) The above highlighted linear programming model has been solved by using ‘solver’ and
the output is shown below.
6

LINEAR PROGRAMMING
Hence,
X1 = Number of units producedof productEC221= 20650
X2 = Number of units producedof productEC496= 100
X3 = Number of units producedof productNC455=2750
X4 = Number of units producedof productNC791 =400
The maximum profit would be $232,700.
Question 4
(a) Formulation of linear programming model
The aim is to determine the suitable investment plant so as to minimize the capital
investment.
Let the decision variables are X1, X2and X3.
X1 = Amount invest in ABC
X2 = Amount invest in CBS
7

LINEAR PROGRAMMING
X3 = Amount invest in NBC
Objective function
Mintotal investment Z =X 1+ X 2+ X 3
Subject to constraints
Short term growth constraints
0.39 X 1+0.26 X 2+0.42 X 3≥ 1000
Intermediate growth constraints
1.595 X 1+ 1.7 X 2+ 1.45 X 3 ≥ 6000
Dividend growth constraints
0.08 X 1+0.04 X 2+0.06 X 3 ≥ 250
Non-negativity constraints; X 1 , X 2∧X 3 ≥0
(b) The above highlighted linear programming model has been solved by using ‘solver’ and
the output is shown below.
Hence,
The total minimum investment would be $3694.75. Further, the optimum amounts invested in
three stocks ABC, CBS and NBC are $2555.25, $1139.50 and $0 respectively.
8