Advanced Control Systems: ElectEng 704 Acrobat Robot Controller Design
VerifiedAdded on 2020/04/07
|15
|852
|131
Homework Assignment
AI Summary
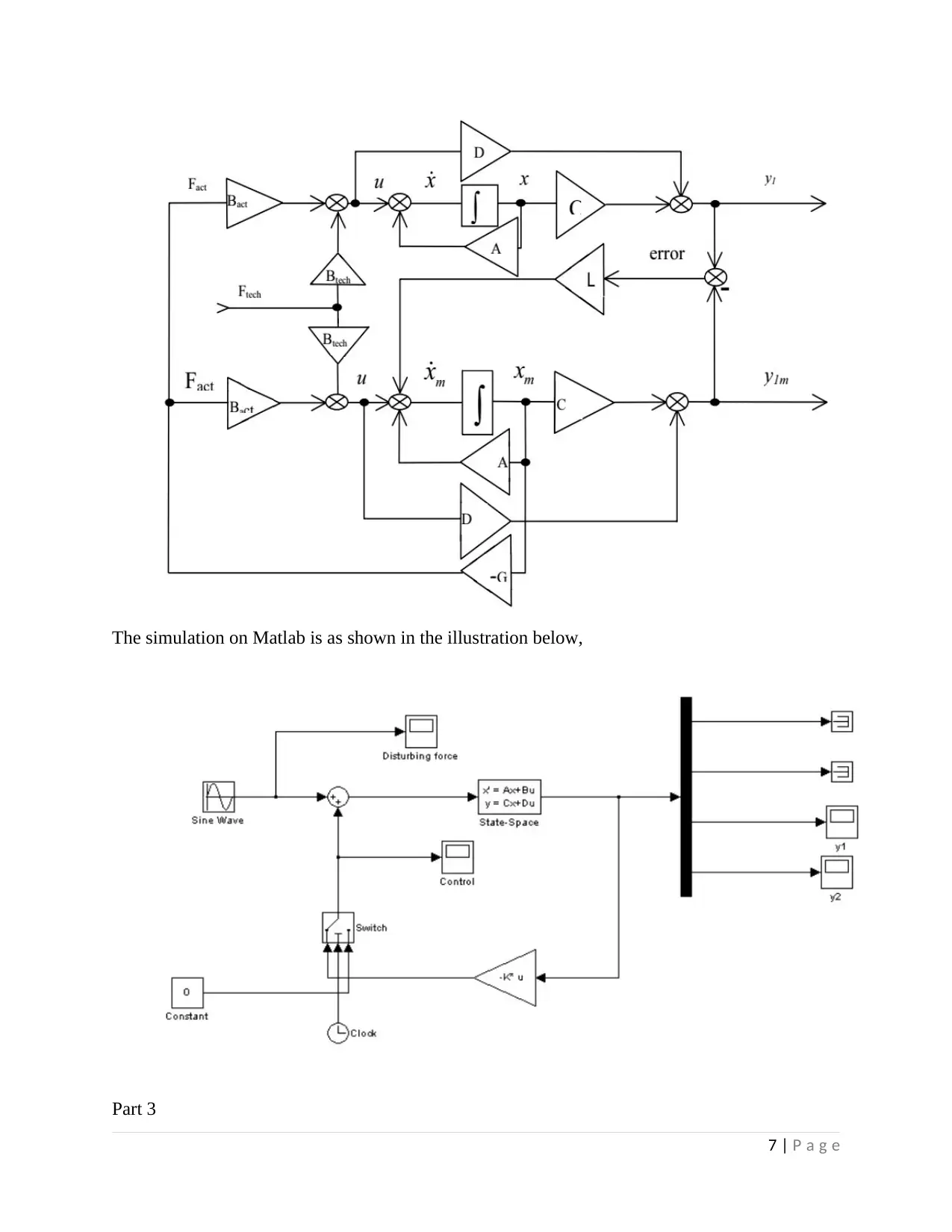
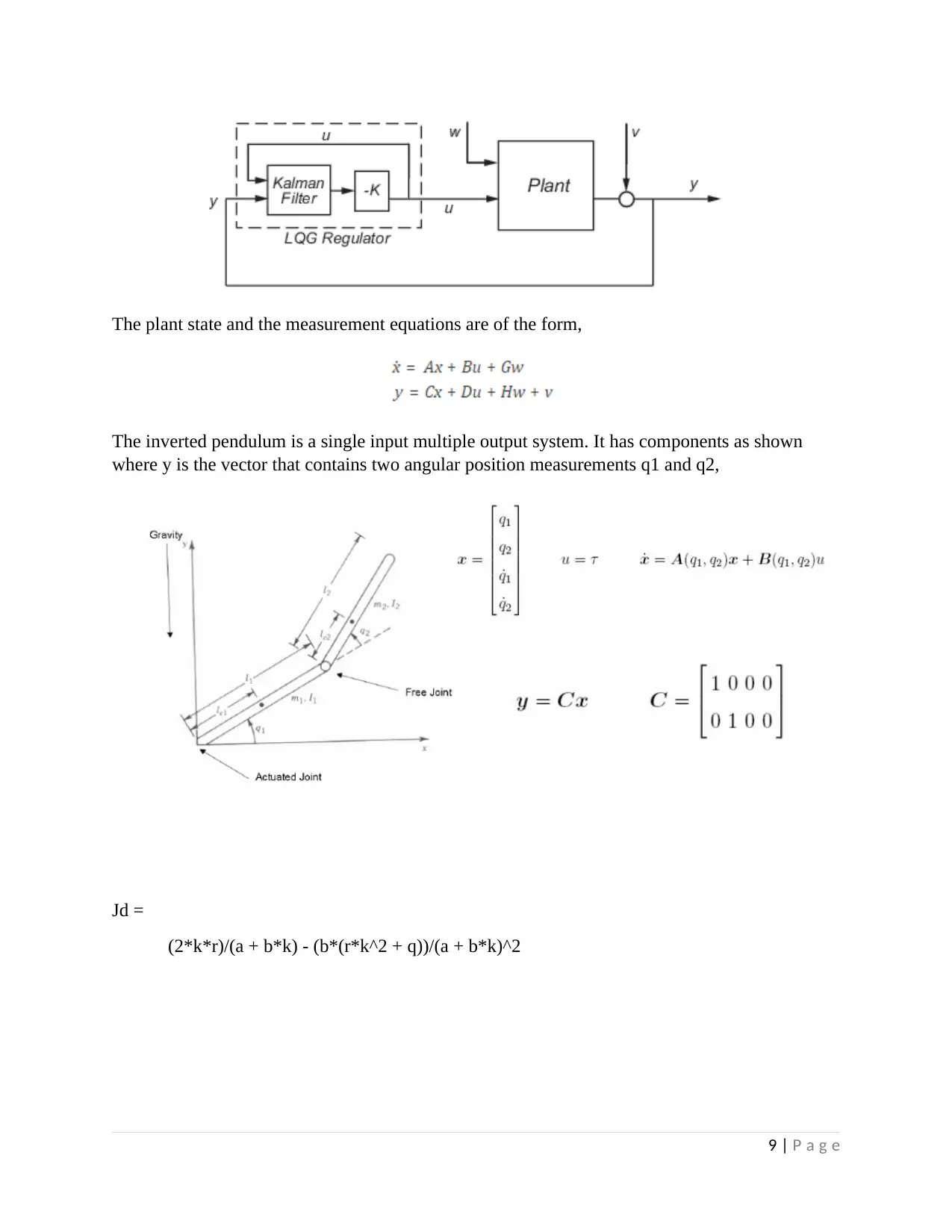
This assignment solution addresses the control of an under-actuated acrobat robot, a two-joint system, within the context of the ElectEng 704 Advanced Control Systems course at the University of Auckland. The solution explores various control methodologies, including Linear Quadratic Regulator (LQR), Linear Quadratic Gaussian (LQG), Loop Transfer Recovery (LTR), and H-infinity (H∞) control. The assignment involves verifying the system's equilibrium, linearizing the system, and designing controllers to stabilize the system about the equilibrium point. The solution includes Matlab simulations to validate the controller designs and estimate the domain of attraction for the stabilizing controllers. The document provides a comprehensive analysis of each control method, comparing their robustness and limitations, with a focus on full-state feedback requirements and considerations for practical implementation. The appendix provides the complete Matlab script used to solve the system requirements.
1 out of 15