Derivative Securities: Portfolio Payoffs, Options, and Forwards

This assignment provides a detailed analysis of derivative securities, focusing on options and forward contracts. It begins with an examination of portfolio payoffs, including calculations for call and put options with varying strike prices, and illustrates trading strategies such as strangle and butterfly spreads. The analysis extends to determining upper and lower boundaries for portfolio payoffs. Furthermore, the assignment covers the pricing of forward contracts, emphasizing the role of risk-free interest rates and the absence of arbitrage opportunities. It also compares the risk profiles of future and forward contracts, highlighting the risk mitigation features of future contracts, such as clearing house guarantees, regulatory oversight, and daily margin adjustments. This document is available on Desklib, a platform offering a wide range of study tools and solved assignments for students.

Running head: INTRODUCTION TO DERIVATIVE SECURITIES
Introduction to Derivative Securities
Name of the Student:
Name of the University:
Authors Note:

INTRODUCTION TO DERIVATIVE SECURITIES
1
Table of Contents
Part A:........................................................................................................................................2
Answer to I:................................................................................................................................2
Answer to II:..............................................................................................................................3
Answer to III:.............................................................................................................................4
Part B:.........................................................................................................................................4
Answer to I:................................................................................................................................4
Answer to II:..............................................................................................................................5
Answer to III:.............................................................................................................................6
Part C:.........................................................................................................................................6
Answer to I:................................................................................................................................6
Answer to II:..............................................................................................................................6
Reference and Bibliography:......................................................................................................8

INTRODUCTION TO DERIVATIVE SECURITIES
2
Part A:
Answer to I:
Description Payoffs
The first payoff is P1(K1), where the portfolio has a short
position and has a payoff [P1(K1) Payoff]
− max (0, K1 − S)
The second payoff is C2(K2), where the portfolio has a call
position and has a payoff [C2(K2) Payoff]
max (0, S − K2)
The portfolio Payoff is mainly calculated by summing both call and short position of
the portfolio, where the equation is as follows.
Portfolio Payoff = P1(K1) Payoff + C2(K2) Payoff
Portfolio Payoff = − max (0, K1 − S) + max (0, S − K2)
Share price range Portfolio payoff Payoff of C2(K2) Payoff of P1(K1)
S ≥ K2 S – K2 S – K2 0
K1 < S < K2 0 0 0
S ≤ K1 S – K1 0 S – K1

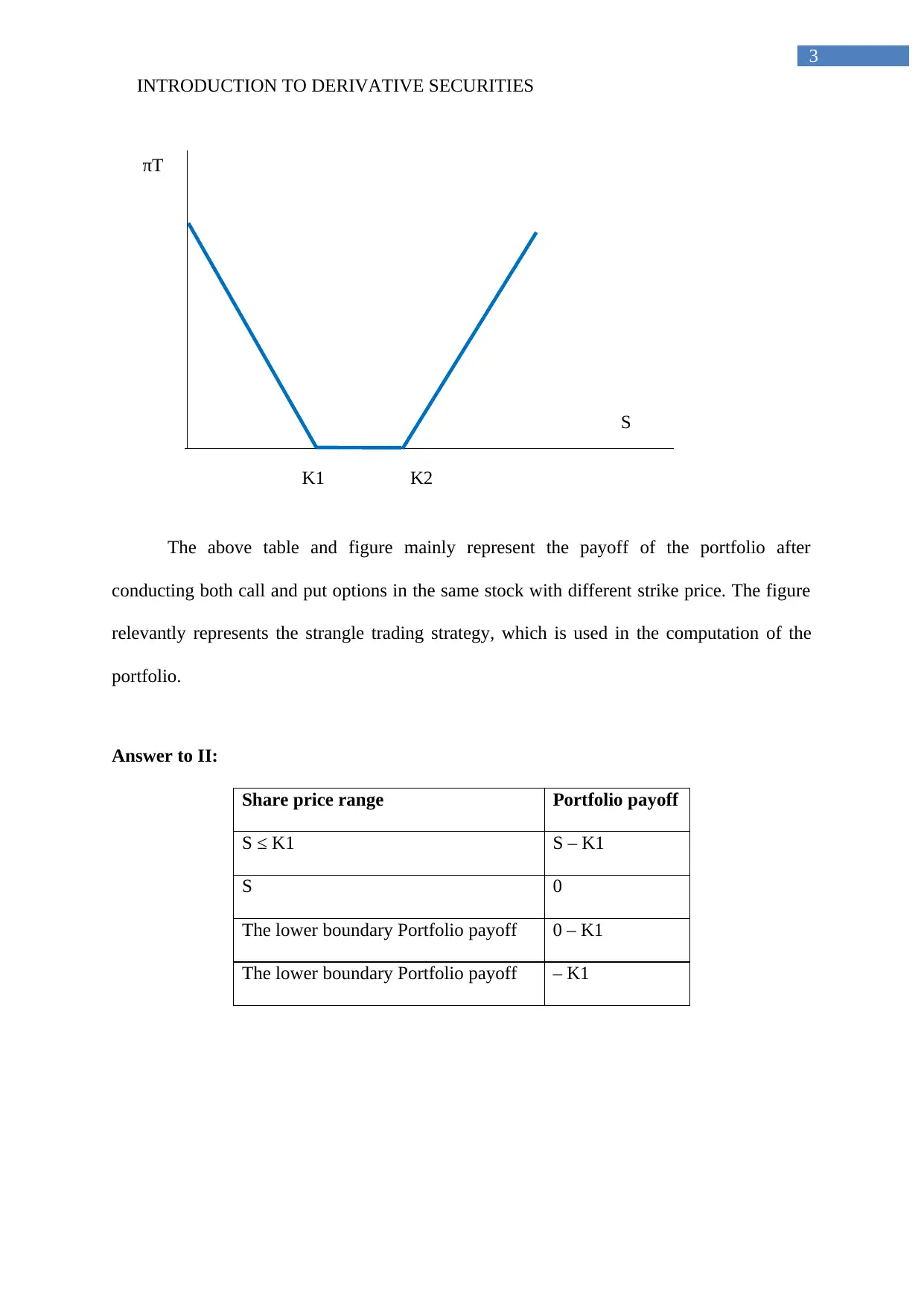
INTRODUCTION TO DERIVATIVE SECURITIES
3
K1 K2
S
πT
The above table and figure mainly represent the payoff of the portfolio after
conducting both call and put options in the same stock with different strike price. The figure
relevantly represents the strangle trading strategy, which is used in the computation of the
portfolio.
Answer to II:
Share price range Portfolio payoff
S ≤ K1 S – K1
S 0
The lower boundary Portfolio payoff 0 – K1
The lower boundary Portfolio payoff – K1

INTRODUCTION TO DERIVATIVE SECURITIES
4
Answer to III:
Share price range Portfolio payoff
S ≥ K2 S – K2
S ∞
The upper boundary Portfolio payoff ∞ – K2
The upper boundary Portfolio payoff ∞
Part B:
Answer to I:
Description Payoffs
The first payoff is P1(K1), where the portfolio has a long
position and has a payoff [P1(K1) Payoff]
max (0, K1 − S)
The second payoff is P2(K2), where the portfolio has a short
position and has a payoff [P2(K2) Payoff]
− max (0, K2 − S)
The second payoff is C3(K3), where the portfolio has a long
position and has a payoff [C3(K3) Payoff]
max (0, S – K3)
The portfolio Payoff is mainly calculated by summing payoffs from long option, short
option and long option in the portfolio, where the equation is as follows.
Portfolio Payoff = P1(K1) Payoff + P2(K2) Payoff + C3(K3) Payoff
Portfolio Payoff = max (0, K1 − S) − max (0, K2 − S) + max (0, S – K3)

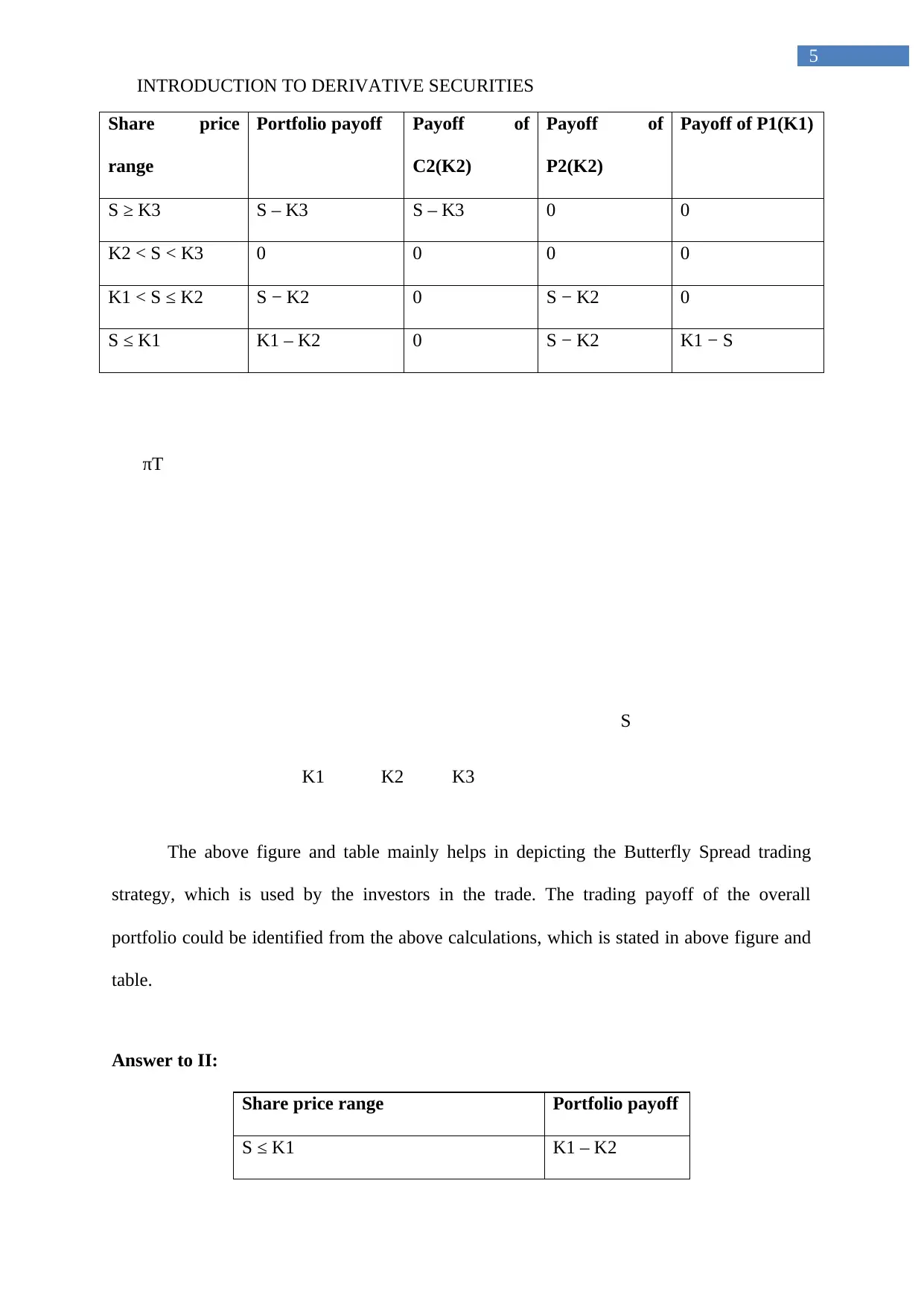
INTRODUCTION TO DERIVATIVE SECURITIES
5
K1 K2
S
πT
K3
Share price
range
Portfolio payoff Payoff of
C2(K2)
Payoff of
P2(K2)
Payoff of P1(K1)
S ≥ K3 S – K3 S – K3 0 0
K2 < S < K3 0 0 0 0
K1 < S ≤ K2 S − K2 0 S − K2 0
S ≤ K1 K1 – K2 0 S − K2 K1 − S
The above figure and table mainly helps in depicting the Butterfly Spread trading
strategy, which is used by the investors in the trade. The trading payoff of the overall
portfolio could be identified from the above calculations, which is stated in above figure and
table.
Answer to II:
Share price range Portfolio payoff
S ≤ K1 K1 – K2

INTRODUCTION TO DERIVATIVE SECURITIES
6
S 0
The lower boundary Portfolio payoff K1 – K2
The lower boundary Portfolio payoff K1 – K2
Answer to III:
Share price range Portfolio payoff
S ≥ K3 S – K3
S ∞
The upper boundary Portfolio payoff ∞ – K3
The upper boundary Portfolio payoff ∞
Part C:
Answer to I:
Forward price = S0 (1 + i)T
The forward contract equation could be identified from the above table, where the
equation assumes no cashflows from the underlying assets for the forward contract term. In
addition, the forward contract value relevantly remains fixed at the trading values, and no
underlying changes in assets value is affected in the forward price. The addition of risk free
interest rate and time is used in calculating the forward price, where no arbitrage position is
detected.
Answer to II:
The relevant feathers that states the least risk of figure contract are depicted as follows.

INTRODUCTION TO DERIVATIVE SECURITIES
7
 The future contracts investors are obligated to pay the outstanding amount of the clearing
house, which is not compulsory for forward contract, as private investors hold it
(Bellalah, Mondher, and Marc Lavielle 2015).
 The regulation followed in figure contract relevantly helps in protecting interest of the
investors and minimise the risk from payment clearing. In addition, the clearing house has
high creditworthiness, where no default inherent risk is detected in future contracts
 Lastly, the position of traders is squared on daily basis, where the profit or loss is depicted
in margin account. Moreover, the trades are mainly allowed when the margin value of
futures trades are relevantly adequate for the trade. Thus, it could be identified that future
contracts have low risk from investment in comparison to forward contracts (Rao,
Sandeep Keshava 2016).

INTRODUCTION TO DERIVATIVE SECURITIES
8
Reference and Bibliography:
Bellalah, Mondher, and Marc Lavielle. "A decomposition of empirical distributions with
applications to the valuation of derivative assets." (2015).
Bichuch, Maxim, Agostino Capponi, and Stephan Sturm. "Arbitrage‐free
XVA." Mathematical Finance 28, no. 2 (2018): 582-620.
Chiarella, Carl, Xue-Zhong He, and Christina Sklibosios Nikitopoulos. "Pricing Derivative
Securities: A General Approach." In Derivative Security Pricing, pp. 207-234. Springer,
Berlin, Heidelberg, 2015.
Rao, Sandeep Keshava. "Equity Valuation: Premium to Interest Rate Structure Model." PES
Business Review 11, no. 1 (2016): 24.
Tebaldi, Claudio, and Pietro Veronesi. "Risk‐Neutral Pricing: Monte Carlo
Simulations." Handbook of Fixed-Income Securities (2015): 435-468.
Wagner, Rodrigo. Mechanism for Market Valuation of State-Owned Enterprises without
Privatization. Inter-American Development Bank, 2017.
Wang, Tiandu, Chenghu Ma, and Qian Sun. "The interaction between security lending
market and security trading market." Pacific-Basin Finance Journal 46 (2017): 309-322.
Yari, Gholamhossein, Mohamadtaghi Rahimi, and Pranesh Kumar. "Multi-period Multi-
criteria (MPMC) Valuation of American Options Based on Entropy Optimization
Principles." Iranian Journal of Science and Technology, Transactions A: Science 41, no. 1
(2017): 81-86.