Derivatives: Statistics and Analysis

This document provides insights on derivatives, statistics, and analysis. It covers topics such as mean, standard deviation, alpha, beta, t-statistics, R-squared, hedging portfolio, and CAPM. The content includes solved assignments and essays.

DERIVATIVES
1
STATISTICS
DERIVATIVES
Student Name:
Name of Institution:

2
> #Importing the dataset
> Data_set<-read.csv("F:/Data.csv")
> #Question 1:
> #Excess daily returns has been calculated by getting the difference between the returns and the
risk- free interest rate.The risk- free rate has been taken to be 2% (0.02). The caluculations have
been done in excel. The values of excess daily returns can be extracted from data set using the
code below.
> Daily_Excess_Returns<-Data_set$Excess_Return #Extracting the daily returns from the data
set.
> Daily_Excess_Returns
[1] -0.45 -2.23 0.38 1.02 0.76 0.66 0.67 -0.23 0.11 0.01 1.07 0.34
[13] -0.55 -0.44 -0.20 -0.22 -0.29 0.05 0.05 -0.45 1.24 1.34 0.52 1.12
[25] 0.47 -0.04 -0.22 0.47 0.45 -0.77 1.12 0.15 0.24 1.25 0.92 -0.53
[37] 0.35 1.41 -0.75 -0.81 0.95 0.29 -2.75 -4.00 2.12 -1.19 -4.24 2.42
[49] 1.17 0.21 2.06 1.78 -0.24 0.19 -0.17 -0.11 2.00 1.05 -1.43 -0.50
[61] -1.43 1.08 1.25 0.14 1.27 0.44 1.88 0.14 -1.61 0.23 0.00 -0.19
[73] -2.39 -0.67 -0.21 -2.83 -2.54 3.67 -3.83 -0.46 2.25 -2.44 0.73 1.49
[85] 0.52 -2.11 0.58 2.22 -0.46 1.00 -0.51 0.86 2.37 -0.22 -0.05 -1.15
[97] -0.14 -2.53 -0.40 2.51 -0.21 -0.83 1.04 -0.82 0.10 1.53 0.82 0.11
[109] 1.67 0.92 -0.21 -0.36 -0.91 0.12 -0.28 -0.12 0.74 -0.62 1.10 -0.19
[121] -0.15 -0.74 1.09 0.49 1.84 0.82 0.39 0.25 -1.37 0.49 0.29 0.71
[133] -0.18 0.80 -0.32 0.87 -0.48 0.18 -0.97 -0.60 -2.18 0.40 -1.74 1.12
[145] 0.03 1.33 -1.15 1.40 1.45 0.69 -0.22 0.14 2.23 0.23 -0.40 0.97
[157] -0.21 -0.60 0.29 0.75 0.38 1.75 -2.64 -2.18 -2.47 0.29 0.21 1.20
[169] 0.23 0.93 0.41 0.29 0.08 -0.57 -0.60 0.75 -1.37 -0.25 -0.21 0.04
[181] -0.01 0.74 0.17 1.42 0.88 -0.07 1.01 -0.50 -0.37 -0.65 -2.09 -0.44
[193] 0.01 0.55 1.07 -0.27 0.60 0.28 -1.57 0.55 -0.44 1.23 -0.54 0.46
[205] 0.43 -0.05 0.57 -0.25 -0.11 -0.87 0.38 -2.19 -0.78 -1.37 -0.10 -4.82
[217] -0.41 2.70 -1.17 3.32 -0.47 -2.39 -0.69 0.85 -0.46 -4.80 3.89 -2.16
[229] -2.31 1.37 2.90 0.16 -0.57 -0.32 0.54 3.04 -0.69 -1.87 -2.62 0.06
[241] -0.61 1.91 -0.27 -4.43 -1.11 1.56 -0.58 2.58 -0.28 3.55 -0.05 0.99
> #Question 1 a: The mean and standard deviation of the excess daily retuns
> Mean_of_excess_dailyretuns<-mean(Daily_Excess_Returns) #The mean of excess daily retuns
> Mean_of_excess_dailyretuns
[1] 0.03130952
#Report
#The mean of daily returns is 0.031. This mean is equivalent to 3.1%. The mean value of the
daily returns is more than the risk- free market return which is 2%. Therefore, it is clear that the
software industry is profitable (Masayuki, 2010)
> Std_deviation_excess_dailyreturns<-sd(Daily_Excess_Returns)# The stdanrd deviation
> Std_deviation_excess_dailyreturns
[1] 1.383512
#Report
#The standard deviation is the measure of the spread of risk (Natalia, et al., 2014). The standard
deviation is also equivalent to the returns.

3
> #Question 1 b:
> #Estimating alpha, Beta, t-statistics and R^2 for gold and software
> #i. Estimating alpha, Beta,t-statistics and R^2 for Software
> software_portfolio_returns<-Data_set$Software_PortforlioReturn
> Software_excessReturn<-Data_set$Software.Excess_Return
> CAMPEstimates1<-lm(software_portfolio_returns~Software_excessReturn)
> summary(CAMPEstimates1)
Call:
lm(formula = software_portfolio_returns ~ Software_excessReturn)
Residuals:
Min 1Q Median 3Q Max
-2.933e-15 -2.701e-17 9.900e-18 4.429e-17 9.691e-16
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.000e-02 1.354e-17 1.477e+15 <2e-16 ***
Software_excessReturn 1.000e+00 9.806e-18 1.020e+17 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.149e-16 on 250 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 1.04e+34 on 1 and 250 DF, p-value: < 2.2e-16
> #ii. Estimating alpha, Beta, t-statistics and R^2 in gold
> gold_portfolioRetuns<-Data_set$Gold_PortflioRetuen
> gold_excessRetuns<-Data_set$Gold_ExcessReturn
> CAMPEstimates2<-lm(gold_portfolioRetuns~gold_excessRetuns)
> summary(CAMPEstimates2)
Call:
lm(formula = gold_portfolioRetuns ~ gold_excessRetuns)
Residuals:
Min 1Q Median 3Q Max
-9.584e-15 9.000e-19 3.760e-17 7.620e-17 1.052e-15
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.000e-02 3.919e-17 5.103e+14 <2e-16 ***
gold_excessRetuns 1.000e+00 2.437e-17 4.103e+16 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

4
Residual standard error: 6.215e-16 on 250 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 1.684e+33 on 1 and 250 DF, p-value: < 2.2e-16
#Report
#The value of alpha is 2.0, the value of Beta is 3.919, the t- value is 5.103 and the R squared
value is 1. The value of alpha represents the return on software industry, the value of Beta
represents the market return. The value of t-statistics is more than the significant level hence
there is a significant difference in the returns of the individual daily returns. The value of R
squared is 1 indicating that the sample explain 100% of the population (Masayuki, 2010).
#Question 1 c : Reason for Hedging portfolio
The reason for hedging portfolio is to spread the risks associated with investments (Itkin &
Andrey, 2013). The spreading of risk through hedging is achieved by portfolio diversification
(De, et al., 2010)
> #Question 2
> #2a. Estimating CAMP. The codes below will give the parameters of CAPM. Therefore, to get
the actual CAPM, the estimated parameters are used to write the model.
> #i. CAPM for softawre
> software_portfolio_returns<-Data_set$Software_PortforlioReturn
> Software_Return<-Data_set$MKT_Ret
> CAMPEstimates3<-lm(software_portfolio_returns~Software_Return)
> summary(CAMPEstimates3)
Call:
lm(formula = software_portfolio_returns ~ Software_Return)
Residuals:
Min 1Q Median 3Q Max
-2.3862 -0.3413 0.0023 0.3325 2.1322
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.01580 0.03870 0.408 0.683
Software_Return 1.30021 0.04063 32.002 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.6141 on 250 degrees of freedom
Multiple R-squared: 0.8038, Adjusted R-squared: 0.803
F-statistic: 1024 on 1 and 250 DF, p-value: < 2.2e-16
> #ii. CAMP for gold

5
> gold_portfolioRetuns<-Data_set$Gold_PortflioRetuen
> gold_Return<-Data_set$MKT_Ret
> CAPMEstimates4<-lm(gold_portfolioRetuns~gold_Return)
> summary(CAPMEstimates4)
Call:
lm(formula = gold_portfolioRetuns ~ gold_Return)
Residuals:
Min 1Q Median 3Q Max
-7.1970 -0.9230 -0.0616 0.7486 7.6693
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.06359 0.09922 -0.641 0.522181
gold_Return 0.36667 0.10417 3.520 0.000513 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.574 on 250 degrees of freedom
Multiple R-squared: 0.04722, Adjusted R-squared: 0.04341
F-statistic: 12.39 on 1 and 250 DF, p-value: 0.0005125
>
#Report
#The value of alpha is 0.06559 indicating that the return on gold industry is 6.6% while the
return on the software industry is 1.6%. The market return in relation to the software industry is
3.9% while the market return in relation to the gold industry is 10%. Both industries demonstrate
that there is a significant difference in the daily returns. The R squared value in relation to the
software industry is 80.38% while in R squared value in relation to the gold industry is 47.22%.
#Question 2b
#Based on the above results, the best hedge is the gold industry. Gold industry is the best hedge
since it has higher returns compared to the software industry.
> #Question 3
> #3a i. Plotting S$P 500 index level as a function of date
> S_and_P500_index.level<-Data_set$SP500_Idx #Extracting the values of S$P500 index level
> Date_Values<-Data_set$Date #Extracting the data values
> plot(S_and_P500_index.level,Date_Values)

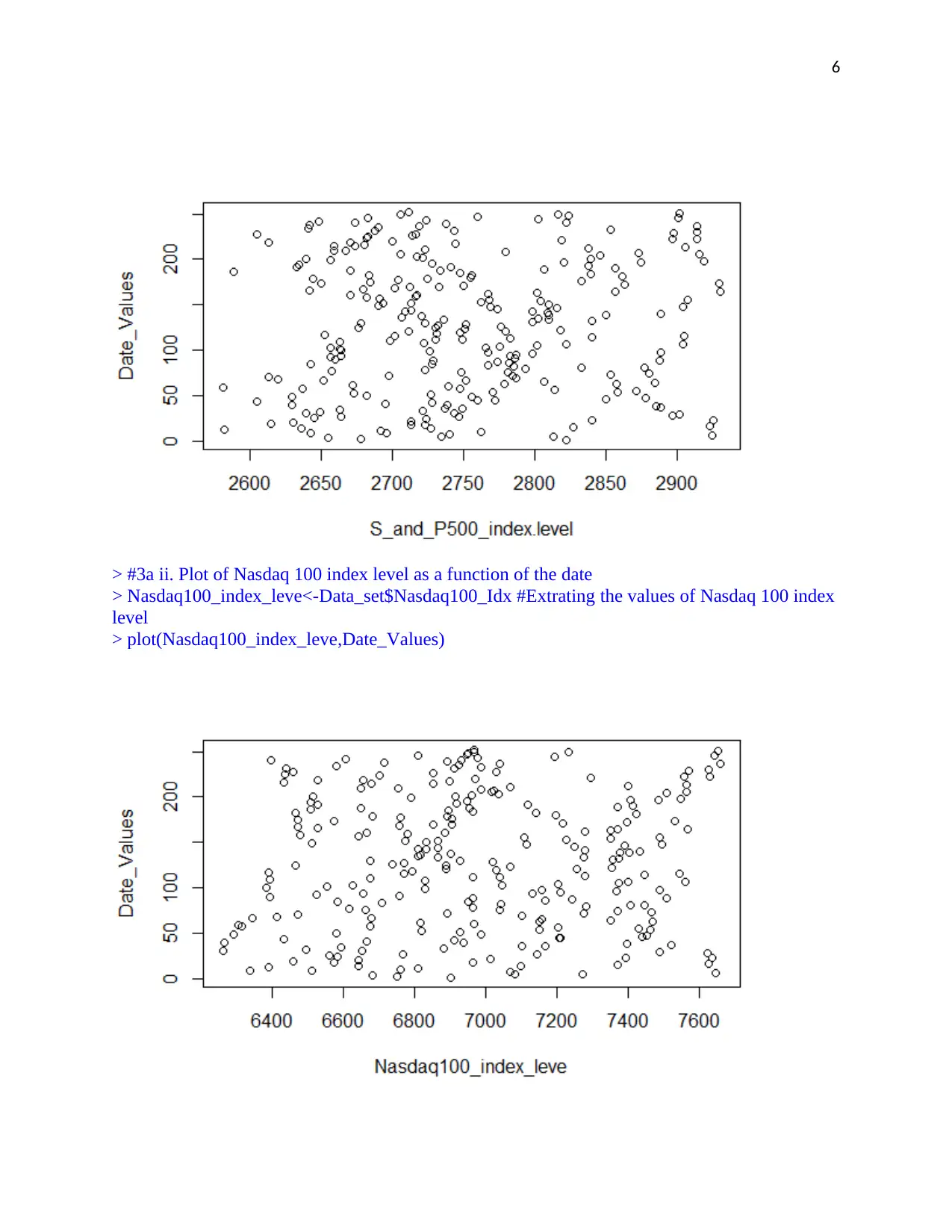
6
> #3a ii. Plot of Nasdaq 100 index level as a function of the date
> Nasdaq100_index_leve<-Data_set$Nasdaq100_Idx #Extrating the values of Nasdaq 100 index
level
> plot(Nasdaq100_index_leve,Date_Values)

7
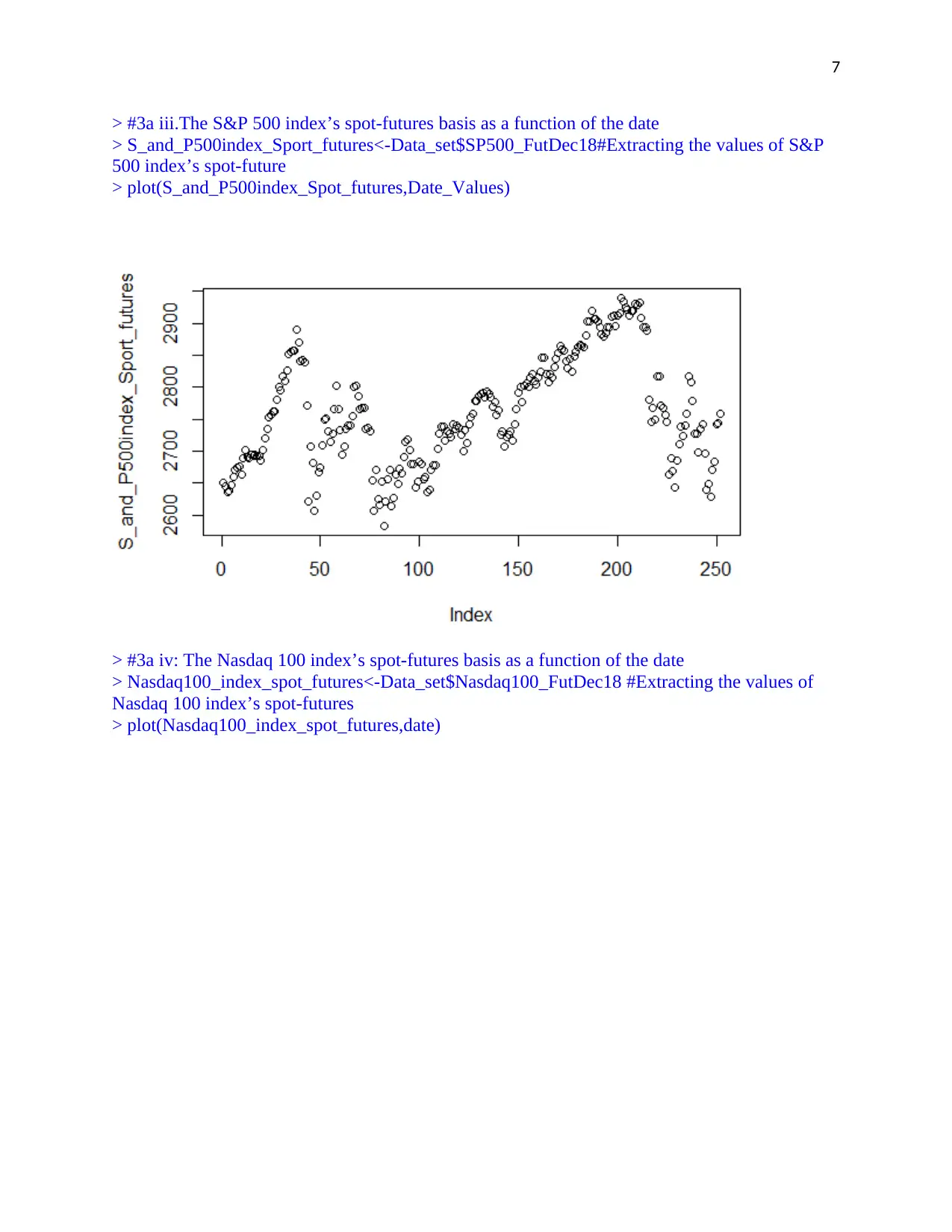
> #3a iii.The S&P 500 index’s spot-futures basis as a function of the date
> S_and_P500index_Sport_futures<-Data_set$SP500_FutDec18#Extracting the values of S&P
500 index’s spot-future
> plot(S_and_P500index_Spot_futures,Date_Values)
> #3a iv: The Nasdaq 100 index’s spot-futures basis as a function of the date
> Nasdaq100_index_spot_futures<-Data_set$Nasdaq100_FutDec18 #Extracting the values of
Nasdaq 100 index’s spot-futures
> plot(Nasdaq100_index_spot_futures,date)

8
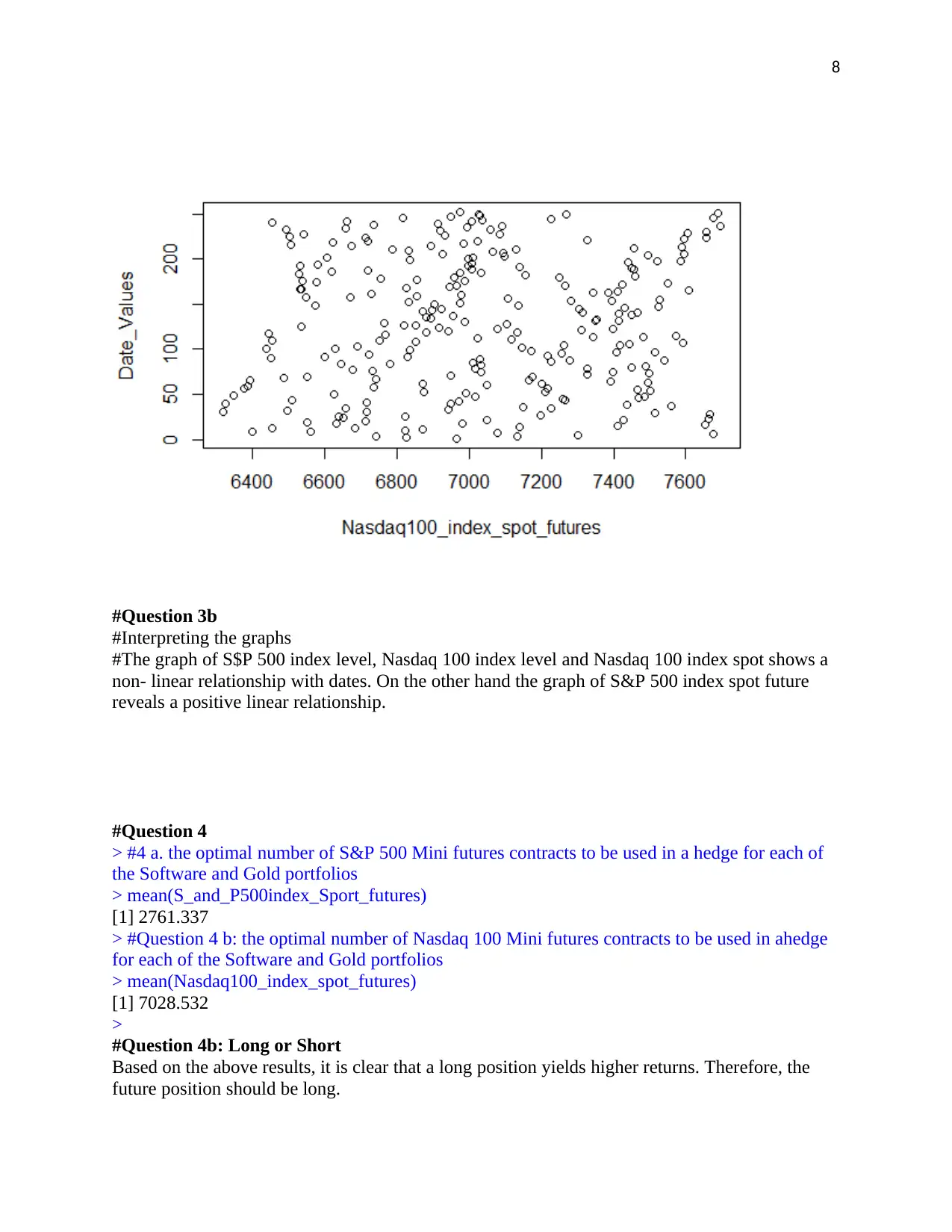
#Question 3b
#Interpreting the graphs
#The graph of S$P 500 index level, Nasdaq 100 index level and Nasdaq 100 index spot shows a
non- linear relationship with dates. On the other hand the graph of S&P 500 index spot future
reveals a positive linear relationship.
#Question 4
> #4 a. the optimal number of S&P 500 Mini futures contracts to be used in a hedge for each of
the Software and Gold portfolios
> mean(S_and_P500index_Sport_futures)
[1] 2761.337
> #Question 4 b: the optimal number of Nasdaq 100 Mini futures contracts to be used in ahedge
for each of the Software and Gold portfolios
> mean(Nasdaq100_index_spot_futures)
[1] 7028.532
>
#Question 4b: Long or Short
Based on the above results, it is clear that a long position yields higher returns. Therefore, the
future position should be long.

9
> #Question 5
> #5 a:Cumulative gain on the Software portfolio is hedged using the S&P 500 Mini
> Day_gain<-1
> Software_size<-Data_set$Softw_Ret
> N<-Software_size[20]
> future_return<-Data_set$RF
> F0<-future_return[19]
> F1<-future_return[152]
> S_and_P500Mini<-Data_set$SP500_Ret
> S<-S_and_P500Mini[152]
> Cumulative_gain1<-Day_gain*N*S*(F1-F0)
> Cumulative_gain1
[1] 0.001220199
>
> #5b the Software portfolio is hedged using the Nasdaq 100 Mini,
> Software_size<-Data_set$Softw_Ret
> N<-Software_size[20]
> future_return<-Data_set$RF
> F00<-future_return[19]
> F11<-future_return[152]
> Nasda100_mini<-Data_set$Nasdaq100_Ret
> S1<-Nasda100_mini[152]
> Cumulative_gain2<-Day_gain*N1*S1*(F1-F0)
> mean(Cumulative_gain2)
[1] -0.0303062
>
> #5c the Gold portfolio is hedged using the S&P 500 Mini
>
> Day_gain<-1
> gold_size<-Data_set$Gold_Ret
> N<-gold_size[20]
> future_return<-Data_set$RF
> F0<-future_return[19]
> F1<-future_return[152]
> S_and_P500Mini<-Data_set$SP500_Ret
> S<-S_and_P500Mini[152]
> Cumulative_gain3<-Day_gain*N*S*(F1-F0)
> Cumulative_gain3
[1] 0.0001135069
>
> # 5D: the Gold portfolio is hedged using the Nasdaq 100 Mini.
> N<-gold_size[20]
> future_return<-Data_set$RF
> F00<-future_return[19]

10
> F11<-future_return[152]
> Nasda100_mini<-Data_set$Nasdaq100_Ret
> S1<-Nasda100_mini[152]
> Cumulative_gain4<-Day_gain*N1*S1*(F1-F0)
> mean(Cumulative_gain4)
[1] -0.0303062
>
#Report
Therefore the cumulative gains are:
For 29 Dec 2017 the cumulative gain is 0.001221, for 29 June 2018 the cumulative gain is -
0.030306 and for 30 November 2018, the cumulative gain is 0.001138069.
> #Question 6
> #A. Hedged portfolio
> hedged_portfolio1<-Software_size[20]+Cumulative_gain
> hedged_portfolio1
[1] -0.428217
> #b
> hedged_portfolio2<-Software_size[20]+Cumulative_gain1
> hedged_portfolio2
[1] -0.4287798
> #c
> hedged_portfolio3<-gold_size[20]+Cumulative_gain3
> hedged_portfolio3
[1] -0.03988649
> #d
> hedged_portfolio4<-gold_size[20]+Cumulative_gain4
>
> #6B
> #the value of the hedged portfolio position on the following three dates: i) 29 December 2017,
ii) 29 June 2018, and iii) 30 November 2018.
> #a
> hedged_position_dec2017<-Software_size[20]+Cumulative_gain
> hedged_position_dec2017
[1] -0.428217
> hedged_position_june2018<-Software_size[145]+Cumulative_gain
> hedged_position_june2018
[1] 0.05178301

11
> hedged_position_nov2018<-Software_size[252]+Cumulative_gain
> hedged_position_nov2018
[1] 1.011783
> #b
> hedged_position_dec2017_1<-Software_size[20]+Cumulative_gain1
> hedged_position_dec2017_1
[1] -0.4287798
> hedged_position_june2018_1<-Software_size[145]+Cumulative_gain1
> hedged_position_june2018_1
[1] 0.0512202
> hedged_position_nov2018_1<-Software_size[252]+Cumulative_gain1
> hedged_position_nov2018_1
[1] 1.01122
> #c
> hedged_position_dec2017_2<-Software_size[20]+Cumulative_gain3
> hedged_position_dec2017_2
[1] -0.4298865
> hedged_position_june2018_2<-Software_size[145]+Cumulative_gain3
> hedged_position_june2018_2
[1] 0.05011351
> hedged_position_nov2018_2<-Software_size[252]+Cumulative_gain3
> mean(hedged_position_nov2018_2)
[1] 1.010114
> #d
> hedged_position_dec2017_3<-Software_size[20]+Cumulative_gain4
> mean(hedged_position_dec2017_3)
[1] -0.4603062
> hedged_position_june2018_3<-Software_size[145]+Cumulative_gain4
> hedged_position_june2018
[1] 0.05178301
> hedged_position_nov2018_3<-Software_size[252]+Cumulative_gain4
> mean(hedged_position_nov2018_3)
[1] 0.9796938
>

12
#Report

13
The graphs shows a linear relationship. The graph demonstrate that the hedging value changes
linearly with time. The relationship is a negative linear relationship.
> #Question 7a
> summary(lm(Daily_Excess_Returns~Data_set$RF))
Call:
lm(formula = Daily_Excess_Returns ~ Data_set$RF)
Residuals:
Min 1Q Median 3Q Max
-4.7705 -0.5530 0.0330 0.7972 3.9395
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.4120 0.4705 0.876 0.382
Data_set$RF -57.6865 70.0552 -0.823 0.411
Residual standard error: 1.384 on 250 degrees of freedom
Multiple R-squared: 0.002705, Adjusted R-squared: -0.001284
F-statistic: 0.6781 on 1 and 250 DF, p-value: 0.411
> #Question 7b
> #Percentage of Daily hedaged portfolio
>
> for (i in 1:n)
{
Daily_Excess_Returns
percentage<-(Daily_Excess_Returns[i]/(Daily_Excess_Returns[i]-1))*100
percentage
}
>
#Question 7C
#Report and interpretation
The mean of daily excess returns is 0.412 which is more than the risk- free rate. The standard
deviation is 0.47. The standard deviation represents the risk factor of the industry. The t-
statistics value is 0.411 which is more than the p- value. Therefore, there is a significant
difference in the average returns of the software industry.

14
> #Question 8
> CAPMUnhedged<-summary(lm(Data_set$MKT_Ret~Data_set$RF))
> CAPMUnhedged
Call:
lm(formula = Data_set$MKT_Ret ~ Data_set$RF)
Residuals:
Min 1Q Median 3Q Max
-4.0693 -0.4113 0.0207 0.5328 2.6307
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.2257 0.3246 0.695 0.488
Data_set$RF -30.0557 48.3339 -0.622 0.535
Residual standard error: 0.9552 on 250 degrees of freedom
Multiple R-squared: 0.001544, Adjusted R-squared: -0.00245
F-statistic: 0.3867 on 1 and 250 DF, p-value: 0.5346
> #Question 8b
> CAPMhedged<-summary(lm(Data_set$MKT_Ret~Data_set$Excess_Return))
> CAPMhedged
Call:
lm(formula = Data_set$MKT_Ret ~ Data_set$Excess_Return)
Residuals:
Min 1Q Median 3Q Max
-1.70650 -0.22035 0.00739 0.25614 1.43209
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.007958 0.026680 0.298 0.766
Data_set$Excess_Return 0.618202 0.019317 32.002 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4234 on 250 degrees of freedom
Multiple R-squared: 0.8038, Adjusted R-squared: 0.803
F-statistic: 1024 on 1 and 250 DF, p-value: < 2.2e-16
>

15
#Question 8 c
#Reporting and interpreting Results
#For part a (unhedged portfolio), the alpha value is 0.2257 which is the daily returns, the Beta
value is 0.3246 which is the market return, the R squared value is 0.0024. The t- statistics value
is 0.488 meaning that there is a significant difference in the average values of the unhedged
portfolio.
#For part b (hedged portfolio), the alpha value is 0.007750 which is the daily returns, the Beta
value is 0.0026 which is the market return, the R squared value is 0.8038. The t- statistics value
is 0.76 meaning that there is a significant difference in the average values of the hedged
portfolio.
> #Question 9
> #Question 9
#A: Calaculating the total initia margin and total maintaince margin for each scenaario
>
> #for scenario a
> Total_initial_margin<-6000*Cumulative_gain + 6000*Cumulative_gain
> Total_initial_margin
[1] 21.39616
> Total_maintainace_margin<-7700*Cumulative_gain+7000*Cumulative_gain
> Total_maintainace_margin
[1] 26.2103
> #for scenario b
> Total_initial_margin1<-6000*Cumulative_gain1 + 6000*Cumulative_gain1
> Total_initial_margin1
[1] 14.64238
> Total_maintainace_margin1<-7700*Cumulative_gain1 + 7000*Cumulative_gain1
> Total_maintainace_margin1
[1] 17.93692

16
> #for scenario c
> Total_initial_margin3<-6000*Cumulative_gain3 + 6000*Cumulative_gain3
> Total_initial_margin3
[1] 1.362082
> Total_maintainace_margin3<-7700*Cumulative_gain3 + 7000*Cumulative_gain3
> Total_maintainace_margin3
[1] 1.668551
> #for scenario d
> Total_initial_margin4<-6000*Cumulative_gain4 + 6000*Cumulative_gain4
> Total_maintainace_margin4<-7700*Cumulative_gain4 +7000*Cumulative_gain4
> mean(Total_maintainace_margin4)
[1] -445.5012
>
> #Question 9 B: Calculating and reporting maximum daily gain
> daily_gain_a<-mean(Total_initial_margin,Total_maintainace_margin)
> daily_gain_a
[1] 21.39616
> daily_gain_b<-mean(c(Total_initial_margin1,Total_maintainace_margin1))
> daily_gain_b
[1] 16.28965
> daily_gain_c<-mean(c(Total_initial_margin3,Total_maintainace_margin3))
> daily_gain_c
[1] 1.515317
> daily_gain_d<-mean(c(Total_initial_margin4,Total_maintainace_margin4))
> daily_gain_d
[1] -404.5878
>
> #Question 9C: Calculating and reporting balance of the margin account and size
> balance_a<-Total_initial_margin - Total_maintainace_margin
> balance_a
[1] -4.814136
> balance_b<-Total_initial_margin1 - Total_maintainace_margin1
> balance_b
[1] -3.294537
> balance_c<-Total_initial_margin3 - Total_maintainace_margin
> balance_c
[1] -24.84822
> balance_d<-Total_initial_margin4 - Total_maintainace_margin4
> mean(balance_d)
[1] 81.82675
#Question 10
Based on the results obtained above, I am highly likely to recommend hedging of portfolio
(Zyuzkina, et al., 2014). Hedging portfolio ensures portfolio diversification. Portfolio
diversification ensures that the risk is spread across the market (Derbali, et al., 2017).

17
References
De, G., M, E., Maggi, M. A. & Tarantala, C., 2010. Book cover Bayesian outlier detection in
Capital Asset Pricing Model. Statistical Modelling, 10(4).
Derbali, et al., 2017. Compliant Capital Asset Pricing Model: new mathematical modeling.
Journal of Asset Management, Volume 5.
Itkin & Andrey, 2013. New solvable stochastic volatility models for pricing volatility
derivatives. Review of Derivatives Research, Volume 16.
Masayuki, I., 2010. Equilibrium preference free pricing of derivatives under the generalized beta
distributions. Review of Derivatives Research, 13(3), p. 36.
Natalia, K., Anton, K. & Ana, R. C., 2014. Extended Finite State Machine based Test Derivation
Strategies for Telecommunication Protocols. Proceedings of the Spring/Summer Young
Researchers' Colloquium on Software Engineering, Issue 8.
Zyuzkina, Halyna & Mykolaiva, 2014. The main features and the principles of description of
derivational morphonology of derivatives of foreign origin in the modern Ukrainian language.
Austrian Journal of Humanities and Social Sciences, 9(10).

18
Appendix
#Question 1
#Excess daily returns has been calculated by getting the difference between the returns and the
risk- free interest rate.The risk- free rate has been taken to be 2% (0.02).
Daily_Excess_Returns<-Data_set$Excess_Return #Extracting the daily returns from the data set.
Daily_Excess_Returns
#Question 1 a: The mean and standard deviation of the excess daily retuns
Mean_of_excess_dailyretuns<-mean(Daily_Excess_Returns) #The mean of excess daily retuns
Mean_of_excess_dailyretuns
Std_deviation_excess_dailyreturns<-sd(Daily_Excess_Returns)# The stdanrd deviation
Std_deviation_excess_dailyreturns
#Question 1 b:
#Estimating alpha, Beta, t-statistics and R^2 for gold and software
#i. Estimating alpha, Beta,t-statistics and R^2 for Software
software_portfolio_returns<-Data_set$Software_PortforlioReturn
Software_excessReturn<-Data_set$Software.Excess_Return
CAMPEstimates1<-lm(software_portfolio_returns~Software_excessReturn)
summary(CAMPEstimates1)
#ii. Estimating alpha, Beta, t-statistics and R^2 in gold
gold_portfolioRetuns<-Data_set$Gold_PortflioRetuen
gold_excessRetuns<-Data_set$Gold_ExcessReturn
CAMPEstimates2<-lm(gold_portfolioRetuns~gold_excessRetuns)
summary(CAMPEstimates2)
#Question 2
#2a. Estimating CAMP. The codes below will give the parameters of CAPM. Therefore, to get
the actual CAPM, the estimated parameters are used to write the model.

19
#i. CAPM for softawre
software_portfolio_returns<-Data_set$Software_PortforlioReturn
Software_Return<-Data_set$MKT_Ret
CAMPEstimates3<-lm(software_portfolio_returns~Software_Return)
summary(CAMPEstimates3)
#ii. CAMP for gold
gold_portfolioRetuns<-Data_set$Gold_PortflioRetuen
gold_Return<-Data_set$MKT_Ret
CAPMEstimates4<-lm(gold_portfolioRetuns~gold_Return)
summary(CAPMEstimates4)
#Question 3
#3a i. Plotting S$P 500 index level as a function of date
S_and_P500_index.level<-Data_set$SP500_Idx #Extracting the values of S$P500 index level
Date_Values<-Data_set$Date #Extracting the data values
plot(S_and_P500_index.level,Date_Values)
#3a ii. Plot of Nasdaq 100 index level as a function of the date
Nasdaq100_index_leve<-Data_set$Nasdaq100_Idx #Extrating the values of Nasdaq 100 index
level
plot(Nasdaq100_index_leve,Date_Values)
#3a iii.The S&P 500 index’s spot-futures basis as a function of the date
S_and_P500index_Sport_futures<-Data_set$SP500_FutDec18#Extracting the values of S&P
500 index’s spot-future
plot(S_and_P500index_Spot_futures,Date_Values)
plot(S_and_P500index_Spot_futures)
#3a iv: The Nasdaq 100 index’s spot-futures basis as a function of the date
Nasdaq100_index_spot_futures<-Data_set$Nasdaq100_FutDec18 #Extracting the values of
Nasdaq 100 index’s spot-futures
plot(Nasdaq100_index_spot_futures,date)

20
#4 a. the optimal number of S&P 500 Mini futures contracts to be used in a hedge for each of the
Software and Gold portfolios
mean(S_and_P500index_Sport_futures)
#Question 4 b: the optimal number of Nasdaq 100 Mini futures contracts to be used in ahedge for
each of the Software and Gold portfolios
mean(Nasdaq100_index_spot_futures)
#Question 5
#5 a:Cumulative gain on the Software portfolio is hedged using the S&P 500 Mini
Day_gain<-1
Software_size<-Data_set$Softw_Ret
N<-Software_size[20]
future_return<-Data_set$RF
F0<-future_return[19]
F1<-future_return[152]
S_and_P500Mini<-Data_set$SP500_Ret
S<-S_and_P500Mini[152]
Cumulative_gain1<-Day_gain*N*S*(F1-F0)
Cumulative_gain1
#5b the Software portfolio is hedged using the Nasdaq 100 Mini,
Software_size<-Data_set$Softw_Ret
N<-Software_size[20]
future_return<-Data_set$RF
F00<-future_return[19]
F11<-future_return[152]
Nasda100_mini<-Data_set$Nasdaq100_Ret
S1<-Nasda100_mini[152]

21
Cumulative_gain2<-Day_gain*N1*S1*(F1-F0)
mean(Cumulative_gain2)
#5c the Gold portfolio is hedged using the S&P 500 Mini
Day_gain<-1
gold_size<-Data_set$Gold_Ret
N<-gold_size[20]
future_return<-Data_set$RF
F0<-future_return[19]
F1<-future_return[152]
S_and_P500Mini<-Data_set$SP500_Ret
S<-S_and_P500Mini[152]
Cumulative_gain3<-Day_gain*N*S*(F1-F0)
Cumulative_gain3
# 5D: the Gold portfolio is hedged using the Nasdaq 100 Mini.
N<-gold_size[20]
future_return<-Data_set$RF
F00<-future_return[19]
F11<-future_return[152]
Nasda100_mini<-Data_set$Nasdaq100_Ret
S1<-Nasda100_mini[152]
Cumulative_gain4<-Day_gain*N1*S1*(F1-F0)
mean(Cumulative_gain4)
#6
#A. Hedged portfolio

22
hedged_portfolio1<-Software_size[20]+Cumulative_gain
hedged_portfolio1
#b
hedged_portfolio2<-Software_size[20]+Cumulative_gain1
hedged_portfolio2
#c
hedged_portfolio3<-gold_size[20]+Cumulative_gain3
hedged_portfolio3
#d
hedged_portfolio4<-gold_size[20]+Cumulative_gain4
#6B
#the value of the hedged portfolio position on the following three dates: i) 29 December 2017, ii)
29 June 2018, and iii) 30 November 2018.
#a
hedged_position_dec2017<-Software_size[20]+Cumulative_gain
hedged_position_dec2017
hedged_position_june2018<-Software_size[145]+Cumulative_gain
hedged_position_june2018
hedged_position_nov2018<-Software_size[252]+Cumulative_gain
hedged_position_nov2018
#b
hedged_position_dec2017_1<-Software_size[20]+Cumulative_gain1
hedged_position_dec2017_1
hedged_position_june2018_1<-Software_size[145]+Cumulative_gain1
hedged_position_june2018_1
hedged_position_nov2018_1<-Software_size[252]+Cumulative_gain1
hedged_position_nov2018_1
#c

23
hedged_position_dec2017_2<-Software_size[20]+Cumulative_gain3
hedged_position_dec2017_2
hedged_position_june2018_2<-Software_size[145]+Cumulative_gain3
hedged_position_june2018_2
hedged_position_nov2018_2<-Software_size[252]+Cumulative_gain3
mean(hedged_position_nov2018_2)
#d
hedged_position_dec2017_3<-Software_size[20]+Cumulative_gain4
mean(hedged_position_dec2017_3)
hedged_position_june2018_3<-Software_size[145]+Cumulative_gain4
hedged_position_june2018
hedged_position_nov2018_3<-Software_size[252]+Cumulative_gain4
mean(hedged_position_nov2018_3)
#Quiz 7a
summary(lm(Daily_Excess_Returns~Data_set$RF))
#7b
#Percentage of Daily hedaged portfolio
for (i in 1:n)
{
Daily_Excess_Returns
percentage<-(Daily_Excess_Returns[i]/(Daily_Excess_Returns[i]-1))*100
percentage
}
#Question 8
CAPMUnhedged<-summary(lm(Data_set$MKT_Ret~Data_set$RF))

24
CAPMUnhedged
#Question 8b
CAPMhedged<-summary(lm(Data_set$MKT_Ret~Data_set$Excess_Return))
CAPMhedged
#Question 9
#A: Calaculating the total initia margin and total maintaince margin for each scenaario
#for scenario a
Total_initial_margin<-6000*Cumulative_gain + 6000*Cumulative_gain
Total_initial_margin
Total_maintainace_margin<-7700*Cumulative_gain+7000*Cumulative_gain
Total_maintainace_margin
#for scenario b
Total_initial_margin1<-6000*Cumulative_gain1 + 6000*Cumulative_gain1
Total_initial_margin1
Total_maintainace_margin1<-7700*Cumulative_gain1 + 7000*Cumulative_gain1
Total_maintainace_margin1
#for scenario c
Total_initial_margin3<-6000*Cumulative_gain3 + 6000*Cumulative_gain3
Total_initial_margin3
Total_maintainace_margin3<-7700*Cumulative_gain3 + 7000*Cumulative_gain3
Total_maintainace_margin3
#for scenario d
Total_initial_margin4<-6000*Cumulative_gain4 + 6000*Cumulative_gain4
Total_maintainace_margin4<-7700*Cumulative_gain4 +7000*Cumulative_gain4
mean(Total_maintainace_margin4)

25
#Question 9 B: Calculating daily gain
daily_gain_a<-mean(Total_initial_margin,Total_maintainace_margin)
daily_gain_a
daily_gain_b<-mean(c(Total_initial_margin1,Total_maintainace_margin1))
daily_gain_b
daily_gain_c<-mean(c(Total_initial_margin3,Total_maintainace_margin3))
daily_gain_c
daily_gain_d<-mean(c(Total_initial_margin4,Total_maintainace_margin4))
daily_gain_d
#Question 9C: Balance of the margin account and size
balance_a<-Total_initial_margin - Total_maintainace_margin
balance_a
balance_b<-Total_initial_margin1 - Total_maintainace_margin1
balance_b
balance_c<-Total_initial_margin3 - Total_maintainace_margin
balance_c
balance_d<-Total_initial_margin4 - Total_maintainace_margin4
balance_d

26