Derivatives Coursework: Regression, Black-Scholes-Merton Formula, and Strategies

This coursework covers regression analysis, Black-Scholes-Merton formula, and various strategies such as bull spread, seagull, and short put butterfly. It includes tables, scatter plots, and ANOVA calculations.

Page1 of32
Derivatives Coursework
Student Name: Student ID:
Unit Name: Unit ID:

Page2 of32
Table of tables
Table 1: Regression analysis including R ................................................................................................ 3
Table2: Strike vs Cobs-Pobs linear line fit plot ........................................................................................ 5
Table3: K residual plot for Cobs-Pobs values .......................................................................................... 5
Table 4: Solution table for σimpl for given K .......................................................................................... 7
Table 5:σimpl for given K ....................................................................................................................
Table6: σimplvs strike rate K plot ...........................................................................................................
Table 7:ANOVA for quadratic fit for table 3 data ................................................................................... 9
Table 8: Regression analysis values excluding three outlier values ....................................................... 11
Table 9: Bull Spread Strategy.................................................................................................................
Table 10: Bull Spread Payoff matrix ......................................................................................................
Table 11: Seagull strategy values ...........................................................................................................
Table 12: Seagull payoff values .............................................................................................................
Table 13: Short put butterflypayoff values ............................................................................................. 1
Table 14: Two-period binomial modelwith European vanilla payoff values ......................................... 19
Table 15: Two-period binomial modelwith Digital payoff values ......................................................... 21
Table 16: Regression Analysis for Question 1 with residual output ...................................................... 26
Table 17: Question 2 Solution for implied volatility .............................................................................. 28
Table 18: Regression Analysis for Question 2 with outliers .................................................................. 30
Table 19: Residual values with outliers for Question 2 .......................................................................... 31
Table 20: Regression Analysis for Question 2 without outliers ............................................................. 31
Table 21: Black Scholes calculation for Question 3 ............................................................................... 32
Table of figures
Figure 1: Scatter plot excluding outliers 10
Figure 2: Bull spread graph ...................................................................................................................
Figure 3: Seagull payoff graph ...............................................................................................................
Figure 4: Residual Plot for Question 1 ................................................................................................... 2

Page3 of32
ANS:1 Put-call parity requires that the following equation to hold
).....(....................0 iKeeSPC rTT
obsobs
−− −=− δ
• Where T=11 months
• obsobs PC , are observed prices of the call and put options
• δis continuously compounded dividend per year
• r is continuously compounded risk free interest per annum
• 0S is current spot price of the stock
• T is option maturity
Now linear regression general form of the equation is )........(.......... iixy βα+=
(i) Comparing equations (i) and (ii) it is obtained that rTT eeS −− −== βα δ ,0 where
KxPCy obsobs =−= ,
(ii) To fit the linear regression model, help of regression tool in excel has been used
Following results have been obtained:
Table 1: Regression analysis including R
Regression Statistics
Multiple R 0.997754
R Square 0.995512
Adjusted R Square 0.995368
Standard Error 3.5137
Observations 33

Page4 of32
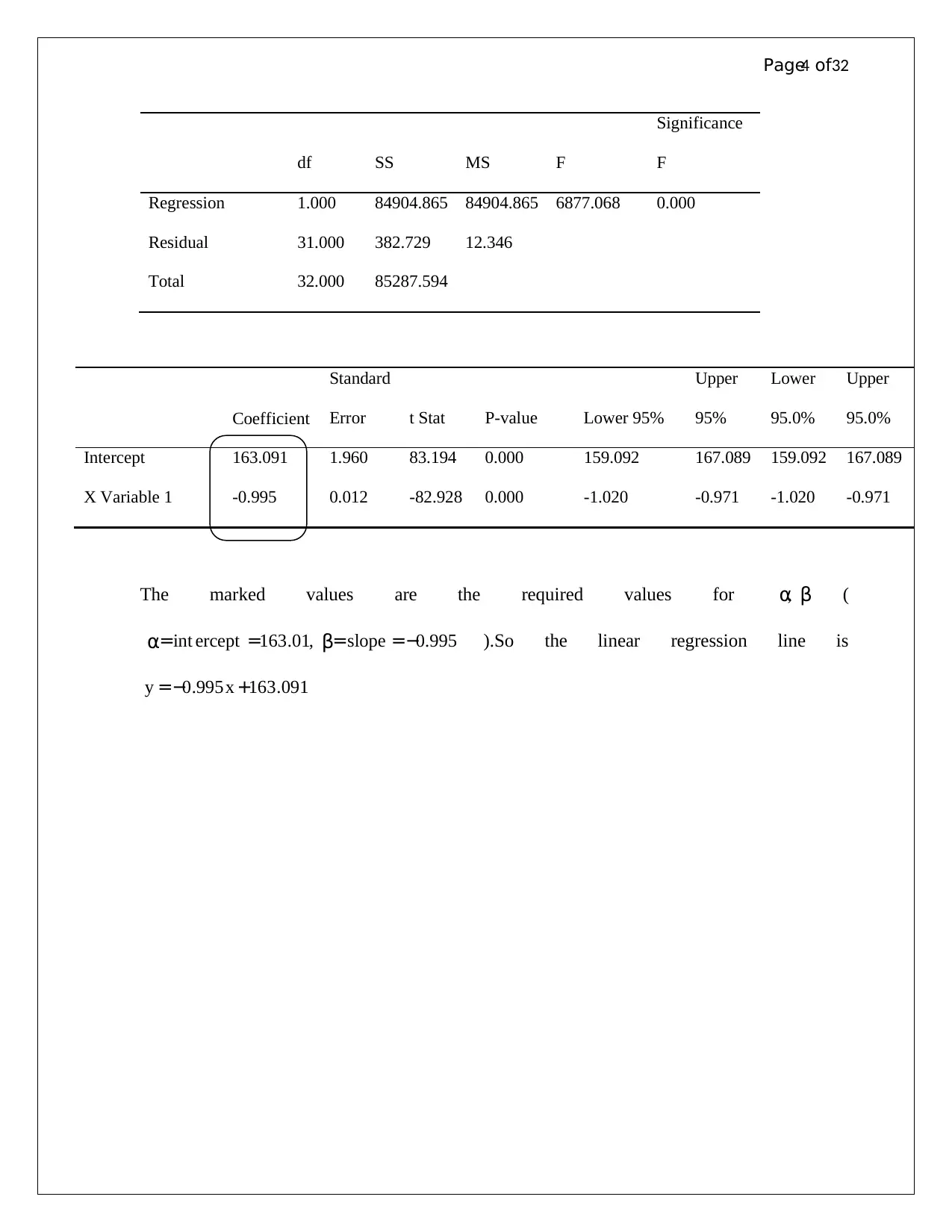
The marked values are the required values for βα, (
995.0,01.163int −==== slopeercept βα ).So the linear regression line is
091.163995.0 +−= xy
df SS MS F
Significance
F
Regression 1.000 84904.865 84904.865 6877.068 0.000
Residual 31.000 382.729 12.346
Total 32.000 85287.594
Coefficient
Standard
Error t Stat P-value Lower 95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 163.091 1.960 83.194 0.000 159.092 167.089 159.092 167.089
X Variable 1 -0.995 0.012 -82.928 0.000 -1.020 -0.971 -1.020 -0.971

Page5 of32
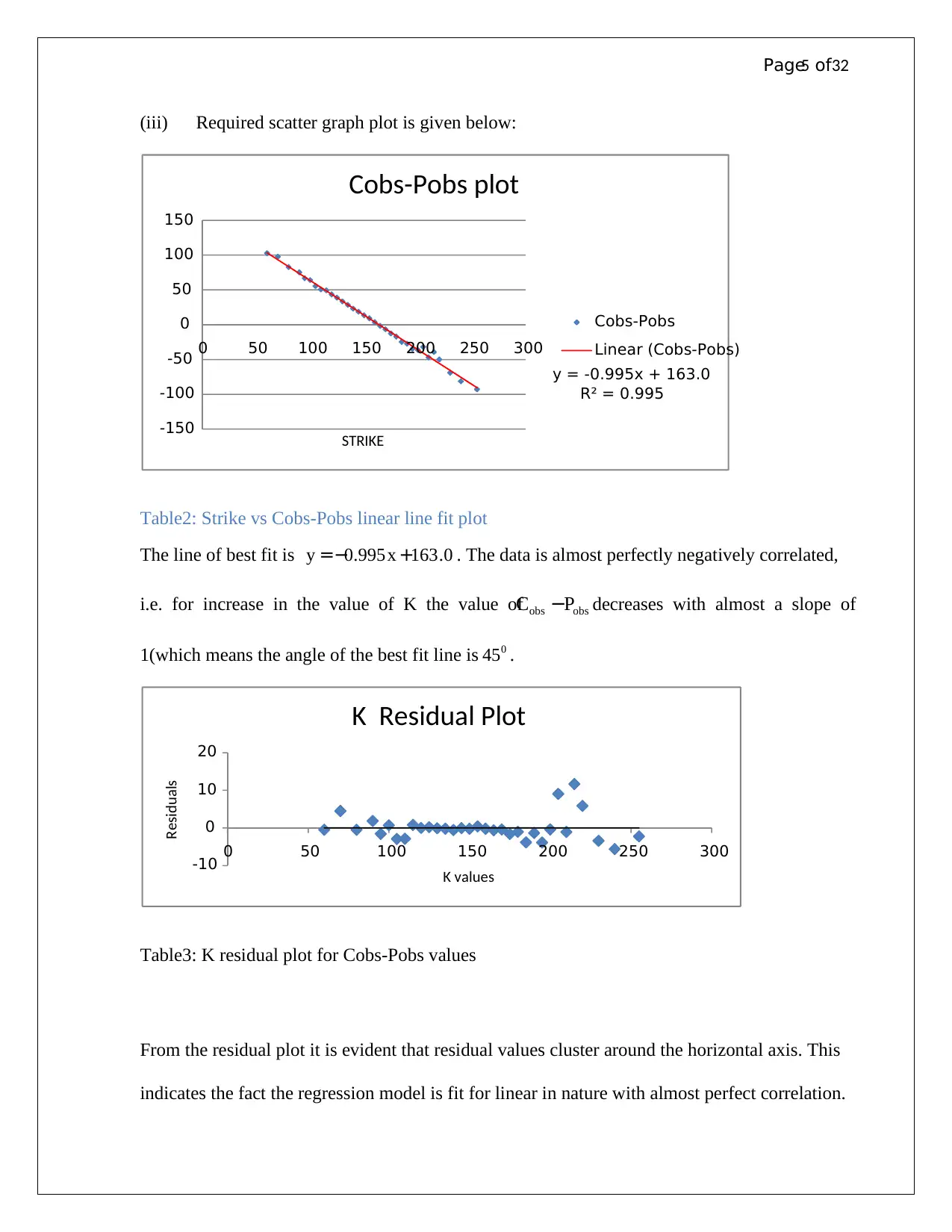
(iii) Required scatter graph plot is given below:
Table2: Strike vs Cobs-Pobs linear line fit plot
The line of best fit is 0.163995.0 +−= xy . The data is almost perfectly negatively correlated,
i.e. for increase in the value of K the value of obsobs PC − decreases with almost a slope of
1(which means the angle of the best fit line is 0
45 .
Table3: K residual plot for Cobs-Pobs values
From the residual plot it is evident that residual values cluster around the horizontal axis. This
indicates the fact the regression model is fit for linear in nature with almost perfect correlation.
y = -0.995x + 163.0
R² = 0.995
-150
-100
-50
0
50
100
150
0 50 100 150 200 250 300
STRIKE
Cobs-Pobs plot
Cobs-Pobs
Linear (Cobs-Pobs)
-10
0
10
20
0 50 100 150 200 250 300
Residuals
K values
K Residual Plot

Page6 of32
Now for 40.1650 =S and T=11/12, 995.0,01.163 −== βα following calculations can be
performed:
0158.0
40.165
01.163
ln*
11
12
ln*
1
ln
0
0
0
0
==>






−==>






−==>






=−>−=
==>
=
−
−
δ
δ
α
δ
α
δ
α
α
δ
δ
ST
S
T
e
S
eS
T
T
And
00547.0
)995.0ln(*
11
12
)ln(*
1
)ln(
==>
−==>
−=−=>
−=−=>
−= −
r
r
T
r
rT
e rT
β
β
β

Page7 of32
ANS:2 (a) Given values are δ = 1.53% per annum, r = 0.49% per annum, T = 11/12 year and
S0 = 165.40.
Black–Scholes–Merton formula gives the option price as:
( ) ( ) ( )2100 ,,,,, dNKedNeSTrKSC rTT
impBSM
−− −= δ
σδ
Where















 +−−= Tr
K
S
T
d impl
impl
*
2
ln
1 2
0
1
σ
δ
σ
and Tdd impl *12 σ−= and ( ).N is the
standard normal cumulative distribution function.
The governing equation provided as ( ) )(..............................0,,,,,0 iTrKSCC impBSMobs =− σδ
Using Excel’s add-in solver equation (i) is solved and the solution is as follows:
Table 4: Solution table for σimpl for given K
K σimpl Cobs
115 27.200000 51.46
120 23.743192 46
125 39.400000 41.78
130 0.268155 37.4
135 0.252982 33
140 0.237571 28.68
145 0.245481 25.64
150 0.237140 22.05
155 0.242571 19.48
160 0.224743 15.8
165 0.220736 13.2
170 0.215498 10.8
175 0.207808 8.53
180 0.210950 7.18
185 0.205065 5.55
190 0.205596 4.5
195 0.198816 3.3
200 0.198853 2.6
205 0.199595 2.06

Page8 of32
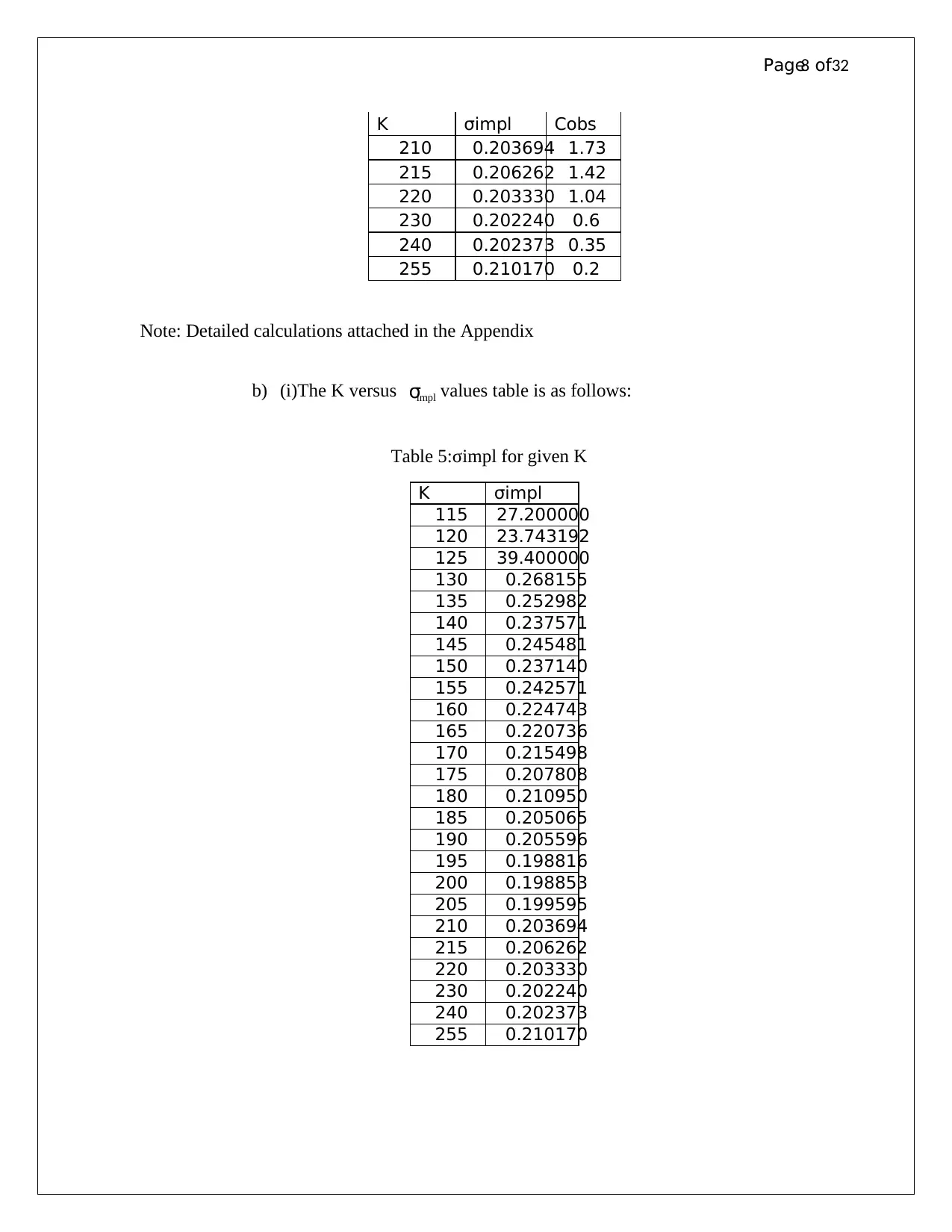
K σimpl Cobs
210 0.203694 1.73
215 0.206262 1.42
220 0.203330 1.04
230 0.202240 0.6
240 0.202373 0.35
255 0.210170 0.2
Note: Detailed calculations attached in the Appendix
b) (i)The K versus implσ values table is as follows:
Table 5:σimpl for given K
K σimpl
115 27.200000
120 23.743192
125 39.400000
130 0.268155
135 0.252982
140 0.237571
145 0.245481
150 0.237140
155 0.242571
160 0.224743
165 0.220736
170 0.215498
175 0.207808
180 0.210950
185 0.205065
190 0.205596
195 0.198816
200 0.198853
205 0.199595
210 0.203694
215 0.206262
220 0.203330
230 0.202240
240 0.202373
255 0.210170

Page9 of32
The graphical plot between K and implσ is as follows:
Table6: σimplvs strike rate K plot
(ii) The quadratic fit for the data in table (3) in the form cbKaKKf ++= 2
)( is as follows:
Table 7:ANOVA for quadratic fit for table 3 data
Regression Statistics
Multiple R 0.720815475
R Square 0.519574949
Adjusted R Square0.475899945
Standard Error 7.381231069
Observations 25
ANOVA
df SS MS F Significance F
Regression 2 1296.292 648.146 11.89639 0.000314689
Residual 22 1198.61754.48257
Total 24 2494.909
Coefficients
Standard
Error t Stat P-value Lower 95% Upper 95%
Intercept 130.305705 31.252544.1694430.000399 65.49189564195.1195144
X Variable 1
-
1.328255552 0.356351 -3.72738 0.00117
-
2.067281355-0.58922975
X Variable 2 0.003307286 0.0009823.3667780.002783 0.0012700590.005344513
y = 0.003x2 - 1.328x + 130.3
R² = 0.519
-10
-5
0
5
10
15
20
25
30
35
40
45
100 150 200 250 300
σimpl
K
σimpl vs K
σimpl
Poly. (σimpl)

Page10 of32
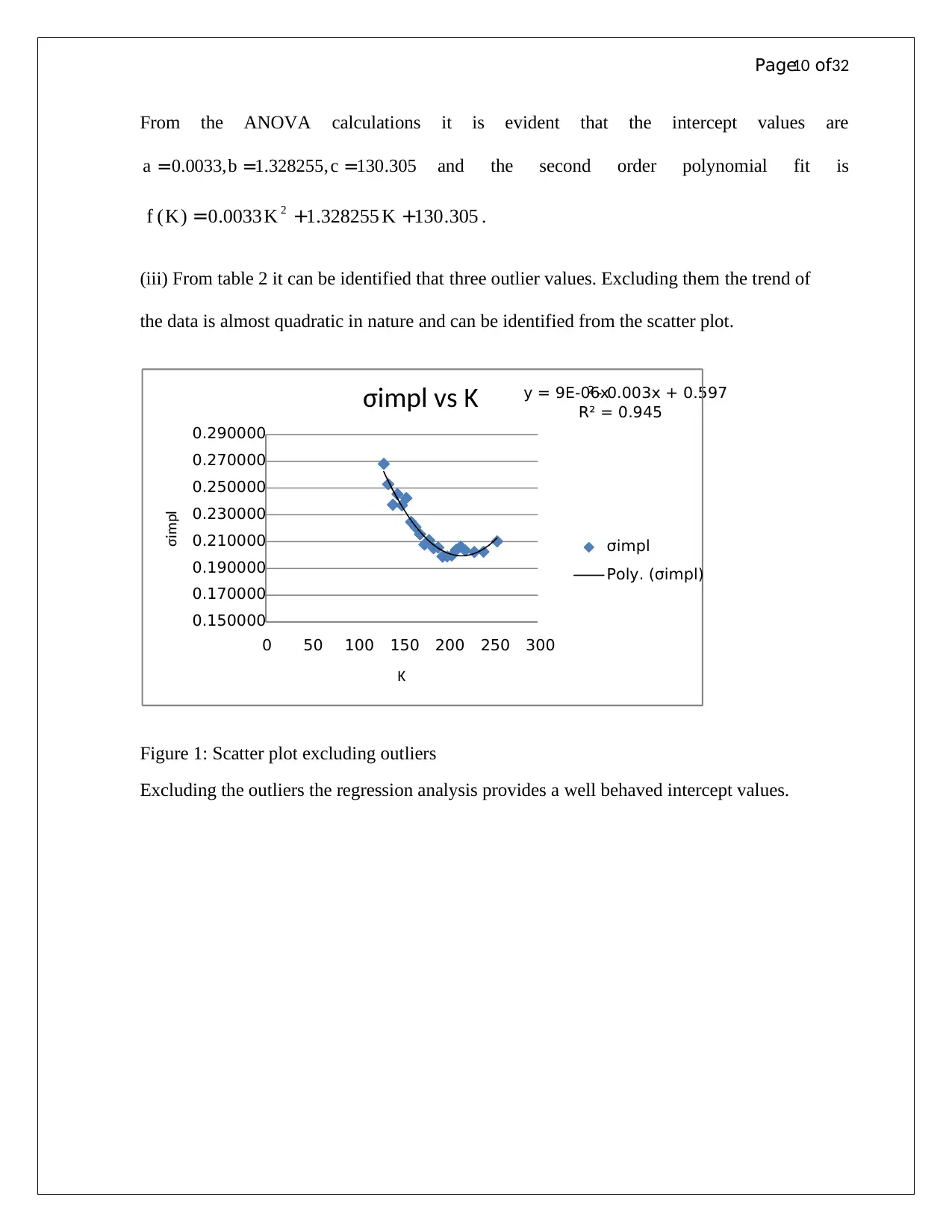
From the ANOVA calculations it is evident that the intercept values are
305.130,328255.1,0033.0 === cba and the second order polynomial fit is
305.130328255.10033.0)( 2 ++= KKKf .
(iii) From table 2 it can be identified that three outlier values. Excluding them the trend of
the data is almost quadratic in nature and can be identified from the scatter plot.
Figure 1: Scatter plot excluding outliers
Excluding the outliers the regression analysis provides a well behaved intercept values.
y = 9E-06x2 - 0.003x + 0.597
R² = 0.945
0.150000
0.170000
0.190000
0.210000
0.230000
0.250000
0.270000
0.290000
0 50 100 150 200 250 300
σimpl
K
σimpl vs K
σimpl
Poly. (σimpl)

Page11 of32
Table 8: Regression analysis values excluding three outlier values
Regression Statistics
Multiple R 0.972541562
R Square 0.94583709
Adjusted R Square 0.940135731
Standard Error 0.0049415
Observations 22
ANOVA
df SS MS F
Significance
F
Regression 2 0.008101874 0.004050937165.897 9.33617E-13
Residual 19 0.00046395 2.44184E-05
Total 21 0.008565824
Coefficients
Standard
Error t Stat P-value Lower 95% Upper 95%
Intercept 0.5970162630.030053865 19.86487483.6E-14 0.5341128010.659919725
X Variable 1 -0.0036848440.000325616-11.316539526.9E-10 -0.00436637
-
0.003003322
X Variable 2 8.5387E-068.60305E-07 9.9252104195.9E-09 6.73807E-061.03393E-05

Page12 of32
ANS:3
(a) Given data values yearTKKyearryearS impl 1,80,70,/%8,/%35,70 210 ====== σ
Black–Scholes–Merton formula gives the option price as:
( ) ( ) ( )2100 ,,,,, dNKedNeSTrKSC rTT
impBSM
−− −= δ
σδ
Where















 +−−= Tr
K
S
T
d impl
impl
*
2
ln
1 2
0
1
σ
δ
σ
and Tdd impl *12 σ−= and ( ).N is the
standard normal cumulative distribution function.
Now for 70=K ,
40357.0
1*
2
35.0*35.0
008.0
70
70
ln
1*35.0
1
1
1
==>





 




 +−+=
d
d
Hence )05357.0(1*35.0040357.02 =−=d
So,
( ) ( ) ( )
)
(1282.12)05357.0(70040357.07035.0,1,0,08.0,70,70 08.00
value
timeNeNeC BSM =−= −−
Now for 80=K ,
022053.0
1*
2
35.0*35.0
008.0
80
70
ln
1*35.0
1
1
1
==>





 




 +−+=
d
d
Hence )327946.0(1*35.0022053.02 =−=d
Now,
( ) ( ) ( )
)(
18.8)327946.0(80022053.07035.0,1,0,08.0,80,70 08.00
valuetime
NeNeC BSM =−= −−
Note: The C(BSM) value got evaluated in Excel using the above formulae.

Page13 of32
(b)
Definition: Bull call spread is for moderate rise in asset price. It is an option strategy which
guides to purchase call options at particular strike rate and sell equal number of calls at a
higher strike rate for same expiration period(Brown 2012).
Explanation of the strategy: In this strategy put call option has higher strike rate than long call
options. Therefore the policy requires an initial cash flow. The maximum gain will be
difference of strike price of long call and short call minus the net cost. The maximum loss
though is limited, which equals to the net premium paid for the options.
The profit for this option increases up to the strike of short call option. Hence gain remains
stationary for security price going above short call strike price. Losses will be occurred for fall
in security prices but becomes stationary if security price goes below long call strike price.
(i) Using the problem of 3(a), it can be calculated using excel sheet (calculation attached)
that for strike value of 70,
Call Option
Value 12.28
Intrinsic Value 0.00
Speculative
Prem. 12.28
Put Option Value 6.90
Intrinsic Value 0.00
Speculative
Prem. 6.90

Page14 of32
And for strike rate 80,
Call Option
Value 8.18
Intrinsic Value 0.00
Speculative
Prem. 8.18
Put Option Value 12.03
Intrinsic Value 10.00
Speculative
Prem. 2.03
Bull spread payoff for all three possible cases calculations:
Table 9: Bull Spread Strategy
Europe
market current value 70
Buy ITM strike price 70
premium -12.28
SELL OTM strike price 80
premium 8.18
Net premium
paid -4.1
Breakeven point 74.1
Table 10: Bull Spread Payoff matrix
On expiry Net Payoff from
Call buy
Net
Payoff
from
Call
Sold
Net
Payoff
68.60 -12.28 8.18 -4.1
69.10 -12.28 8.18 -4.1
69.60 -12.28 8.18 -4.1
70.00 -12.28 8.18 -4.1
70.10 -12.18 8.18 -4
70.60 -11.68 8.18 -3.5
71.10 -11.18 8.18 -3
71.60 -10.68 8.18 -2.5

Page15 of32
72.10 -10.18 8.18 -2
72.60 -9.68 8.18 -1.5
On expiry Net Payoff from
Call buy
Net
Payoff
from
Call
Sold
Net
Payoff
73.10 -9.18 8.18 -1
73.60 -8.68 8.18 -0.5
74.10 -8.18 8.18 0
74.60 -7.68 8.18 0.5
75.10 -7.18 8.18 1
75.60 -6.68 8.18 1.5
76.10 -6.18 8.18 2
76.60 -5.68 8.18 2.5
77.10 -5.18 8.18 3
77.60 -4.68 8.18 3.5
78.10 -4.18 8.18 4
78.60 -3.68 8.18 4.5
79.10 -3.18 8.18 5
79.60 -2.68 8.18 5.5
80.00 -2.28 8.18 5.9
80.10 -2.18 8.08 5.9
80.60 -1.68 7.58 5.9
81.10 -1.18 7.08 5.9
81.60 -0.68 6.58 5.9
82.10 -0.18 6.08 5.9
82.60 0.32 5.58 5.9
83.10 0.82 5.08 5.9

Page16 of32
8.18
0 70 74.1 80
-12.8 Break Even Point
Figure 2: Bull spread graph
(ii) The cost for implementing the strategy will be =(-12.28+8.18)=(4.1)
Hence outlay cost will be 4.1 X (the number of shares each contract has)
(c) (i) For the seagull strategy the following holds:
Table 11: Seagull strategy values
Europe Market Current Market Price 70
Buy 2 ATM Call OptionStrike Price 70
pays Premium (2*12.28) 24.56
Sells 1 ITM Call OptionStrike Price 60
receives Premium 17.87
Sells 1 OTM Call OptionStrike Price 80
receives Premium 8.18
Break Even Point upper78.51
Break Even Point lower61.49

Page17 of32
The payoff table for the policy is:
Table 12: Seagull payoff values
On expiry market
Closes at
Net Payoff from ATM
Calls purchased
Net Payoff from
ITM Call sold
Net Payoff from
OTM Call sold
Net
Payoff
52.5 -24.56 17.87 8.18 1.49
55 -24.56 17.87 8.18 1.49
57.5 -24.56 17.87 8.18 1.49
60 -24.56 17.87 8.18 1.49
61.49 -24.56 16.38 8.18 0
62.5 -24.56 15.37 8.18 -1.01
65 -24.56 12.87 8.18 -3.51
67.5 -24.56 10.37 8.18 -6.01
70 -24.56 7.87 8.18 -8.51
72.5 -19.56 5.37 8.18 -6.01
75 -14.56 2.87 8.18 -3.51
77.5 -9.56 0.37 8.18 -1.01
78.51 -7.54 -0.64 8.18 0
80 -4.56 -2.13 8.18 1.49
82.5 0.44 -4.63 5.68 1.49
85 5.44 -7.13 3.18 1.49
87.5 10.44 -9.63 0.68 1.49
90 15.44 -12.13 -1.82 1.49
92.5 20.44 -14.63 -4.32 1.49
95 25.44 -17.13 -6.82 1.49
97.5 30.44 -19.63 -9.32 1.49
100 35.44 -22.13 -11.82 1.49

Page18 of32
17.87 8.18
60 70 80
12.28
Figure 3: Seagull payoff graph
(ii) Cost of seagull strategy (short call) is = (1 sell ITM + 2 buy ATM + 1 sell OTM)X (the
number of shares each contract has). Hence the cost of seagull strategy will be less
than bull strategy because of the bear effect in seagull.
(iii) The alternative model is short put butterfly with following strategy:
Table 13: Short put butterfly payoff values
Europe Market Current Market Price 70
Sells 1 ITM put OptionStrike Price Kp 60
receives Premium 3.252707516
Buy 2 ATM put OptionStrike Price K1 70
pays
Premium
(2*6.90024289527396) 13.80048579
Sells 1 OTM put OptionStrike Price K2 80
receives Premium 12.03187329
Break Even Point upper 78.51590498
Break Even Point lower 61.48409502
premium profit 1.484095018
Here the investor would get the extra cash as the premium received for initiating the position.

Page19 of32
ANS: 4. (a) du
de
q
u
deuyerastrSHere
tr
t
−
−
=======
∆
∆
*
* ,
1
,,5.0%,30%,5.0,100 σ
σ .
Here u is stock price move-up factor per period and d= stock price move-down factor per
period, q is risk neutral probability of an upward movement
(i) 236311.15.0*3.0* === ∆ eeu tσ
808858.0
236311.1
11 ===u
d
4530208.0
808858.0236311.1
808858.05.0*005..0*
=
−
−
=
−
−
=
∆ e
du
de
q
tr
(ii) For binomial stock pricing with one-year time period split into two six-month
intervals and assuming a two-period binomial model, the tree is obtained as below:
Table 14: Two-period binomial model with European vanilla payoff values
solution
price 100 u 1.236311 =>magnitudeOf up jump
strike
(assume) 100 d 0.808858 =>magnitude
Of down
jump
time(years) 0.5 a 1.002503
volatility 30% q 0.453021 =>probabilityOf up jump
risk free rate 0.50% 1-q 0.546979 =>probability
Of down
jump
dividend 0%
time
point 0 0.5 1
stock 152.8465
option 52.84652
stock 123.6311
option 23.8808
stock 100 100
option 10.79149 0
stock 80.88579
option 0
stock 65.42511
option 0

Page20 of32
The value of the parameters, which are u, d, q were obtained from answer 4a (i).
There are two options in binomial model of pricing. Either the price will go up with
probability 0.453021 or will go down with probability 0.546979. Jump magnitudes are
1.236311 and 0.808858 for the up and down jump for each unit. The tree is calculated for two
periods that is for three time points that are 0, 0.5 and 1 year. Hence going up prices were
calculated by multiplying previous step price by q and subsequently down prices were
calculated by multiplying previous step price by 1-q.
(b) The option prices at the end of one year (t=1) were calculated by taking the maximum
value between zero and the difference between current stock price (S T) and strike price (K).
The calculation of the option prices at time T=1 was obtained from the payoff profile
0,0}0,max{ ≤>− TTT SforandKSforKS . But for the in the money values option prices
were all zero. Consequently previous option prices were evaluated by the formula [q × Option
up + (1−q) × Option down] × exp (- r × Δt). Hence for example at time t=0.5, the option price
for the first leg of the tree for time 0.5 was calculated as
[0.453021*52.84652+0.546979*0]*exp (-0.50%*0.5) = 23.8808. Option price at time t=0 was
10.79149.

Page21 of32
(c) For binomial stock pricing with one-year time period split into two six-month intervals and
assuming a two-period binomial model, the tree is obtained as below. The value of the
parameters u, d, q were obtained from answer 4a (i).
Table 15: Two-period binomial model with Digital payoff values
solution
price 100 u 1.236311 =>magnitude
Of up
jump
strike 100 d 0.808858 =>magnitude
Of down
jump
time(years) 0.5 a 1.002503
volatility 30% q 0.453021 =>probability
Of up
jump
risk free rate 0.50% 1-q 0.546979 =>probability
Of down
jump
dividend 0%
time
point 0 0.5 1
152.8465
1
123.6311
1
stock 100 100
option 0.45189 0
80.88579
0 65.42511
0
The option prices at the end of one year (t=1) were calculated by the payoff profile of digital
option. Hence option price will be 1 where stock price is greater than strike price (100) and 0
where it is less than strike price(Bali 2011).
Consequently previous option prices were evaluated by the formula [q × Option up + (1−q) ×
Option down] × exp (- r×Δt). Hence for example at time t=0.5, the option price for the first leg

Page22 of32
of the tree for time 0.5 was again 1 for stock price 123.6311, but for 80.88579 the option price
calculated as [0*0.453021+0*0.546979]* 05.*005.0−
e =0. For time t=0 the option price for 100 is
[1*0.453021+0*0.546979]* 05.*005.0−
e =0.45189]. It is to be noted that instead of stock price
being 100, option price is calculated by discounting rate.
(d) The payoff profile of the pay-later strategy is as follows:
KSforVKSTtimeatPayoff TT >−− 1.}0,max{: where V is the price of pay later option.
Given payoff is



<
>−−
= KSfor
KSforcS
LC
T
TT
T ,0
,100
(i) Now from part (b) payoff of vanilla call option was
0,0}0,max{ ≤>− TTT SforandKSforKS and from part (c) payoff profile of digital call
option was KSforandKSfor TT ≤> 01 . Strike price here is K=100.
Combining the facts it is obtained that for pay-later strategy the payoff profile can be rewritten
as:
( ) ( ) ( ) ( )



≤
>−
=



≤
>−−
= KS
KScalldigitalofpayoffccallvanillaofpayoff
KS
KScKS
LC
T
T
T
TT
T ,0
,*
,0
,1*
which clearly expresses payoff pay-later strategy as linear combination of vanilla call and
digital call payoff values.
(ii) At initiation of contract at time t=0 pay later Option is zero.Which implies that at t=0
88.23
45189.0
79149.10 === optioncalldigital
optioncallvanilla
c
(iii) The buyer pays price ‘c’ at time Tt = if vanilla option has any value. The pay later
option is priced at t=0. To get the premium seller will wait till time Tt = . Hence it can be
said that ( ) ( ))0,,,,** 2 ==− trKSVanillaedNc rT σ where ( )2dN is probability of finishing

Page23 of32
in the money by Black Scholes formula. So ( ) ( ))0,,,,*
2
== trKSVanilla
dN
e
c
rT
σ which
implies ( )
( ))0,,,,
)0,,,,
=
=
= trKSdigital
trKSVanilla
c σ
σ .
(e)
(i) At time t, the standard put call parity equation is
( ) PSKeCPSKstrikeofvaluepresentC tTr +=+=>+=+ −−
00 , where
C= call premium
K= strike rate of call and put
r=annual interest rate
T=time in years
S0=initial price of underlying
The put-call parity r e l at io ns hip comes nicely from some simple steps. The true
expr essi on considering the payoff of pay later calls and put options:
( )[ ] ( )[ ] KSppSKccKS TTT −=+−−−+−− ++
(1) At expiration t im e, we get:
( )[ ] ( )[ ] TTT SppSKKccKS ++−−=++−− ++
(2) Now multiplying each side by the d isc ou nt factor e−r (T−t) :
( ) ( )[ ] ( ) ( ) ( )[ ] ( ) T
tTr
T
tTrtTr
T
tTr SeppSKeKeccKSe −−
+
−−−−
+
−− ++−−=++−− 1*1*
Taking the conditional expectations for risk neutral measure regarding the s t oc k price:
( ) ( )[ ][ ] ( )
[ ]
( ) ( )[ ][ ] ( )
[ ]sSSeEsSppSKeE
sSKeEsSccKSeE
tT
tTrQ
tT
tTrQ
t
tTrQ
tT
tTrQ
=+=+−−
==+=+−−
−−
+
−−
−−
+
−−
1*
1*

Page24 of32
From risk neutral pricing theory t h e discounted v a l u e of a risky asset is a Martingale.
H e n c e the first term is the price of a Call option for Pay later at time t, the firs t term in RHS
of the equality is the price of a P a y l a t e r Put option attim e t (Mencia 2013).The second
term on the LHS is the price of Call option for Digital call and the second term on the RHS i s
price of Put option for Digital call stock at time t. The second expectations on b o t h the sides
are simply a deterministic function and therefore expectation goes out of calculation.
Hence the put-call parity relationsh ip is :
( ) ttt
tTr
tt SdigitalPplaterPayPKedigitalCclaterPayC ++=++ −− )(*)()(*)(
Where ‘c>0’ and ‘p>0’ are the option premiums for call and put options for Pay-later strategy.
(ii) The European pay later put option has the following payoff:



>
≤−−
= 100,0
100,100
T
TT
T S
SpS
LP , where ‘p>0’.
At time t=0 the value of the put option is zero for pay later, i.e. ( ) 0=laterpayPt .
The previous part of the question gives: 1,0%,5.0,88.23,100,100 ====== TtrcKSt
Again from Table 15, ( ) ( ) 0,54811.045189.0 ===>= tatdigitalPdigitalC tt since



>
≤
=



≤
>
−=−= 100,0
100,1
100,0
100,1
11
T
T
T
T
TT S
S
S
S
DP
And from Table 14 ( ) 79149.10)(*)( ==+ vanillaCdigitalCclaterPayC ttt
Hence
233.19
54811.0
541802.10
54811.0
1007503122.9979149.10
10054811.0*0*10079149.10 5.0*005.0
==
−+
==>
++=+ −
p
pe

Page25 of32
Reference Lists
Bali, T.G., Brown, S.J. and Caglayan, M.O., 2011. Do hedge funds' exposures to risk factors
predict their future returns?. Journal of financial economics, 101(1), pp.36-68.
Brown, R., 2012. Analysis of investments & management of portfolios.
Mencia, J. and Sentana, E., 2013. Valuation of VIX derivatives. Journal of Financial
Economics, 108(2), pp.367-391.

Page26 of32
Appendix
Table 16: Regression Analysis for Question 1 with residual output
Regression Statistics
Multiple R
0.99775
4
R Square
0.99551
2
Adjusted R
Square
0.99536
8
Standard
Error 3.5137
Observation
s 33
ANOVA
df SS MS F
Significa
nce F
Regression 1.000
84904.86
5
84904.
865
6877.
068 0.000
Residual 31.000 382.729 12.346
Total 32.000
85287.59
4
Coeffici
ents
Standard
Error t Stat
P-
value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 163.091 1.960 83.194 0.000 159.092
167.08
9 159.092 167.089
X Variable 1 -0.995 0.012
-
82.928 0.000 -1.020 -0.971 -1.020 -0.971
RESIDUAL OUTPUT
Observation Predicted Y Residuals
1 103.3606-0.490582
2 93.40558 4.504416
3 83.45059-0.500587
4 73.49559 1.854411
5 68.51809-1.578091
6 63.54059 0.719408
7 58.56309-2.923093
8 53.58559-2.885594
9 48.6081 0.801904
10 43.6306 0.019403
11 38.6531 0.216902
12 33.6756 -0.0856
13 28.6981 -0.198101

Page27 of32
14 23.7206 -0.550602
15 18.7431 -0.053103
16 13.7656 -0.215605
17 8.788106 0.421894
18 3.810607-0.210607
19 -1.16689 -0.623109
20 -6.14439 -0.40561
21 -11.1219 -1.598111
22 -16.0994 -1.020612
23 -21.0769 -3.823114
24 -26.0544 -1.345615
25 -31.0319 -3.868116
26 -36.0094 -0.390618
27 -40.9869 9.046881
28 -45.9644 -1.05562
29 -50.9419 11.66188
30 -55.9194 5.859377
31 -65.8744 -3.425625
32 -75.8294 -5.620628
33 -90.7619 -2.238132
Figure 4: Residual Plot for Question 1
-10
-5
0
5
10
15
0 50 100 150 200 250 300
Residuals
K values
K Residual Plot

Page28 of32
Table 17: Question 2 Solution for implied volatility
St
rik
e
K
σim
pl So r δ T
σimpl
*√T
ln(S
o/K
)
(r-
δ+(σimp
l^2)/2)*
T
d1=((L)
+(M))/
(K)
d2=d1-
σimpl*
√T
C(BS
M)
C
o
bs diff
11
5
27.2
000
00
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
26.04
2017
0.3
634
35
339.083
800
13.034
598
-
13.007
419
163.0
9645
64
5
1.
4
6
-
111
.63
6
12
0
23.7
431
92
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
22.73
2375
88
0.3
208
75
258.370
0567
11.379
84578
-
11.352
53011
163.0
9645
64
4
6
-
117
.09
6
12
5
39.4
000
00
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
37.72
2628
05
0.2
800
53
711.487
9333
18.868
46233
-
18.854
16571
163.0
9645
64
4
1.
7
8
-
121
.31
6
13
0
0.26
815
5
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.256
7388
07
0.2
408
32
0.02255
7408
1.0259
05443
0.7691
66635
37.39
9999
63
3
7.
4
3.6
9E-
07
13
5
0.25
298
2
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.242
2114
39
0.2
030
92
0.01893
3191
0.9166
58583
0.6744
47144
32.99
9999
58
3
3
4.1
6E-
07
14
0
0.23
757
1
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.227
4571
6
0.1
667
24
0.01546
838
0.8009
98043
0.5735
40883
28.67
9999
83
2
8.
6
8
1.7
5E-
07
14
5
0.24
548
1
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.235
0300
67
0.1
316
33
0.01721
9566
0.6333
34315
0.3983
04248
25.63
9999
91
2
5.
6
4
8.5
E-
08
15
0
0.23
714
0
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.227
0447
02
0.0
977
31
0.01537
4648
0.4981
66819
0.2711
22117
22.04
9999
21
2
2.
0
5
7.8
9E-
07
15
5
0.24
257
1
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.232
2441
72
0.0
649
42
0.01656
8678
0.3509
68305
0.1187
24133
19.47
9999
32
1
9.
4
8
6.7
6E-
07
16
0
0.22
474
3
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.215
1752
69
0.0
331
93
0.01275
0198
0.2135
15084
-
0.0016
60186
15.79
9999
98
1
5.
8
2.3
6E-
08
16 0.22 165. 0.0 0.0 0.9 0.211 0.0 0.01193 0.0679 - 13.20 1 -

Page29 of32
5 073
6
4000
00
049
00
153
00
166
67
3382
79
024
21
1934 15963 0.1434
22316
0000
02
3.
2
1.7
E-
08
17
0
0.21
549
8
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.206
3237
92
-
0.0
274
3
0.01088
4754
-
0.0801
98704
-
0.2865
22497
10.80
0000
97
1
0.
8
-
9.7
E-
07
17
5
0.20
780
8
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.198
9609
4
-
0.0
564
2
0.00939
2728
-
0.2363
60281
-
0.4353
21221
8.530
0009
69
8.
5
3
-
9.7
E-
07
18
0
0.21
095
0
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.201
9692
35
-
0.0
845
9
0.00999
5786
-
0.3693
34875
-
0.5713
0411
7.179
9998
6
7.
1
8
1.4
E-
07
18
5
0.20
506
5
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.196
3350
32
-
0.1
119
9
0.00887
3722
-
0.5252
00822
-
0.7215
35854
5.550
0008
68
5.
5
5
-
8.7
E-
07
19
0
0.20
559
6
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.196
8430
85
-
0.1
386
6
0.00897
36
-
0.6588
17602
-
0.8556
60687
4.500
0004
44
4.
5
-
4.4
E-
07
19
5
0.19
881
6
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.190
3514
77
-
0.1
646
3
0.00771
6842
-
0.8243
4839
-
1.0146
99867
3.299
9994
78
3.
3
5.2
2E-
07
20
0
0.19
885
3
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.190
3876
87
-
0.1
899
5
0.00772
3736
-
0.9571
35681
-
1.1475
23367
2.599
9994
66
2.
6
5.3
4E-
07
20
5
0.19
959
5
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.191
0978
62
-
0.2
146
4
0.00785
9196
-
1.0820
84322
-
1.2731
82184
2.059
9992
97
2.
0
6
7.0
3E-
07
21
0
0.20
369
4
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.195
0221
45
-
0.2
387
4
0.00861
6819
-
1.1799
88711
-
1.3750
10856
1.729
9998
38
1.
7
3
1.6
2E-
07
21
5
0.20
626
2
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.197
4804
21
-
0.2
622
7
0.00909
9258
-
1.2820
10567
-
1.4794
90989
1.419
9997
11
1.
4
2
2.8
9E-
07
22
0
0.20
333
0
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.194
6737
42
-
0.2
852
6
0.00854
8933
-
1.4214
13221
-
1.6160
86963
1.039
9993
06
1.
0
4
6.9
4E-
07

Page30 of32
23
0
0.20
224
0
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.193
6304
99
-
0.3
297
1
0.00834
6385
-
1.6596
87612
-
1.8533
18111
0.599
9991
17
0.
6
8.8
3E-
07
24
0
0.20
237
3
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.193
7574
69
-
0.3
722
7
0.00837
0978
-
1.8781
27145
-
2.0718
84614
0.349
9990
22
0.
3
5
9.7
8E-
07
25
5
0.21
017
0
165.
4000
00
0.0
049
00
0.0
153
00
0.9
166
67
0.201
2225
21
-
0.4
329
0.00984
5251
-
2.1024
0638
-
2.3036
289
0.199
9992
92
0.
2
7.0
8E-
07
Table 18: Regression Analysis for Question 2 with outliers
Regression Statistics
Multiple R
0.720815
475
R Square
0.519574
949
Adjusted R
Square
0.475899
945
Standard
Error
7.381231
069
Observation
s 25
ANOVA
df SS MS F
Significa
nce F
Regression 2 1296.292
648.1
46
11.89
639
0.000314
689
Residual 22 1198.617
54.48
257
Total 24 2494.909
Coefficie
nts
Standard
Error t Stat
P-
value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept
130.3057
05 31.25254
4.169
443
0.000
399
65.49189
564
195.119
5144 65.4919
195.119
5
X Variable 1
-
1.328255
552 0.356351
-
3.727
38
0.001
17
-
2.067281
355
-
0.58922
975
-
2.06728
-
0.58923
X Variable 2
0.003307
286 0.000982
3.366
778
0.002
783
0.001270
059
0.00534
4513 0.00127
0.00534
5

Page31 of32
Table 19: Residual values with outliers for Question 2
RESIDUAL OUTPUT
Observation Predicted Y Residuals
1 21.295170955.904829
2 18.539953985.203238
3 15.9501013 23.4499
4 13.5256129-13.2575
5 11.2664888-11.0135
6 9.172728988-8.93516
7 7.244333464-6.99885
8 5.481302228-5.24416
9 3.883635282-3.64106
10 2.451332624-2.22659
11 1.184394256-0.96366
12 0.0828201770.132678
13 -0.8533896131.061198
14 -1.6242351151.835185
15 -2.2297163272.434782
16 -2.669833252.875429
17 -2.9445858843.143402
18 -3.0539742293.252828
19 -2.9979982853.197593
20 -2.7766580522.980352
21 -2.389953532.596215
22 -1.8378847192.041215
23 -0.2376542290.439895
24 2.024033416-1.82166
25 6.656797053-6.44663
Table 20: Regression Analysis for Question 2 without outliers
SUMMARY OUTPUT
Regression Statistics
Multiple R
0.97254
1562
R Square
0.94583
709
Adjusted R
Square
0.94013
5731
Standard 0.00494

Page32 of32
Error 15
Observatio 22
ANOVA
df SS MS F
Significa
nce F
Regression 2
0.008101
874
0.00405
0937
165.
897
9.33617
E-13
Residual 19
0.000463
95
2.44184
E-05
Total 21
0.008565
824
Coefficie
nts
Standard
Error t Stat
P-
valu
e
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept
0.59701
6263
0.030053
865
19.8648
748
3.6E-
14
0.53411
2801
0.65991
9725
0.53411
2801
0.65991
9725
X Variable 1
-
0.00368
4844
0.000325
616
-
11.3165
3952
6.9E-
10
-
0.00436
637
-
0.00300
3322
-
0.00436
6366
-
0.00300
3322
X Variable 2
8.5387E-
06
8.60305E
-07
9.92521
0419
5.9E-
09
6.73807
E-06
1.03393
E-05
6.73807
E-06
1.03393
E-05
Table 21: Black Scholes calculation for Question 3
Black-Scholes Option Pricing Model
k=70 k=80 k=60
Time to Expiration 1 Time to Expiration 1 Time to Expiration 1
Exercise Price 70.00 Exercise Price 80.00 Exercise Price 60.00
Current Stock Price70.00 Current Stock Price 70.00 Current Stock Price 70.00
Volatility 35.00% Volatility 35.00% Volatility 35.00%
Risk-Free Rate 8.00% Risk-Free Rate 8.00% Risk-Free Rate 8.00%
d1 0.4036 d1 0.022053d1 0.844002
d2 0.0536 d2 -0.32795 d2 0.494002
N(d1) 0.6567 N(d1) 0.508797N(d1) 0.800666
N(d2) 0.5214 N(d2) 0.371476N(d2) 0.689348
Call Option Value 12.28 Call Option Value 8.18 Call Option Value 17.87
Intrinsic Value 0.00 Intrinsic Value 0.00 Intrinsic Value 10.00
Speculative Prem.12.28 Speculative Prem. 8.18
Speculative
Prem. 7.87
Put Option Value 6.90 Put Option Value 12.03 Put Option Value 3.25
Intrinsic Value 0.00 Intrinsic Value 10.00 Intrinsic Value 0.00
Speculative Prem. 6.90 Speculative Prem. 2.03
Speculative
Prem. 3.25