Descriptive Statistics in Healthcare

This presentation provides an overview of descriptive statistics in healthcare. It covers measures of central tendency and variability, frequency distribution, histogram, mean, median, mode, range, boxplot, percentile, and standard deviation. The presentation explains the importance of these statistical measures in healthcare decision-making and performance evaluation.

DESCRIPTIVE STATISTICS IN
HEALTHCARE
The basic understanding and importance of statistics in
healthcare.

INTRODUCTION
This is widely used in health care sector as it guides to make decisions
as:
1. The health care industry benefits from significant consumer "demographic"
statistics that can expect the sorts of services.
2. Health care companies measures the performance of success or failure.
• Descriptive statistics summarizes variables of sample of population.
• There are several measures in descriptive statistics like frequency, mean,
range, percentile, median, mode and standard deviation and plots like
histogram and box plot.
• Specifically, it can be expressed by measures of central tendency and
measures of variability.
• Measures of central tendency includes mean, median and mode.
• Measures of variability includes standard deviation, variance, skewness and
kurtosis.

FREQUENCY
• Frequency is the number of occurrence of an observation within an interval.
• The width of the interval depends on the size of the data and aim of the
study.
• The intervals are mutually exclusive and exhaustive.
• Frequency is always presented in a tabular or graphical plots (Consoli,
Recupero & Petkovic, 2019).
• For example, height of students can be distributed in different intervals.
• In measuring the height of 50 students (assume), they can be split in three
groups short, medium and tall.
• The interval used to create groups must not overlap each other and should
not contain all the observations.

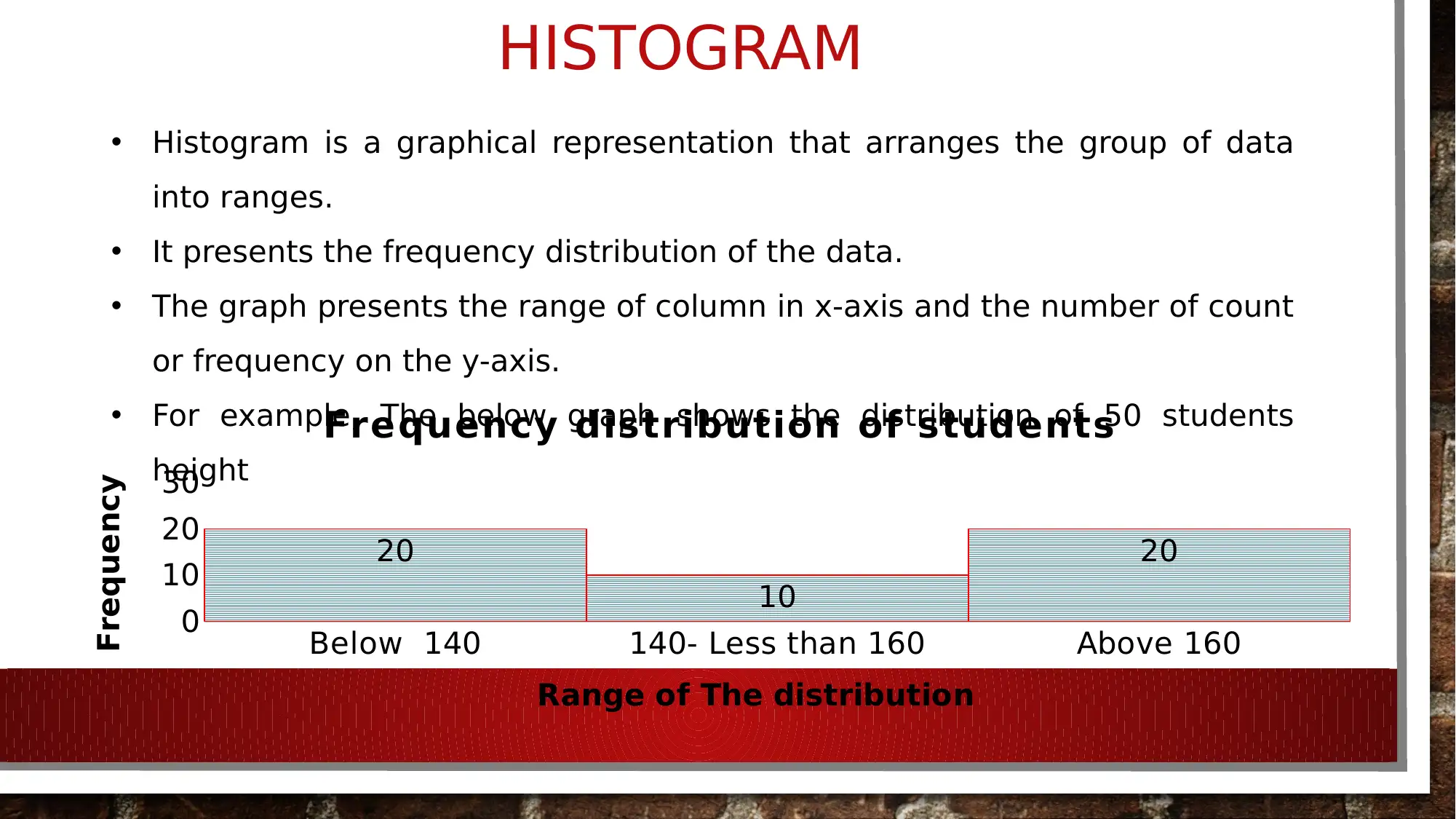
HISTOGRAM
• Histogram is a graphical representation that arranges the group of data
into ranges.
• It presents the frequency distribution of the data.
• The graph presents the range of column in x-axis and the number of count
or frequency on the y-axis.
• For example, The below graph shows the distribution of 50 students
height
Below 140 140- Less than 160 Above 160
0
10
20
30
20
10
20
Frequency distribution of students
Range of The distribution
Frequency

MEAN
• A mean shows the average of the set of the data with more than two
observations.
• There are several methods to compute mean like arithmetic mean and
geometric mean (Solomon & Morgan, 2018).
• Generally arithmetic mean (AM) is used due to its computational technique.
• Arithmetic mean is computed using the following formula, where 𝜇= mean of
x, f presents the frequency of x,
• For example, the computation of mean is shown for the distribution of 50
students height:
• The value indicates that the average height of students is 149.06 cms.

MEDIAN
• The median is the middle most value of the sorted series.
• This can describe the data set more than the mean, by adding information.
• It is preferable more than mean when the data has outliers that potentially able
to skew the data.
• For odd numbers of data set, median is the value which is in the middle that
divides the data set into two equal parts.
• Fro even numbers of data set, the middle pair must be determined and the
average value of those two data points is the median.
• Example, there is 50 students in the observation, hence the middle pair is 25th
and 26th data point. These are 150 and 151 respectively. Hence the median for
the height of the students is 150.5 cm (Chatfield, 2018).

MODE
• Mode is defended as the most frequent number in the data set of numbers.
• In other terms, the maximum frequency provides the mode of the data set of
numbers.
• Mode is another measure of central tendency and as important as Mean and
Median.
• There may exist more than one mode. This happens due to same number of
highest frequency of data set.
• The distribution with one mode is called “Unimodal” and the distribution with
two mode is called “Bimodal”.
• In the example, there maximum frequency is 3 and it is found for two specific
heights. One is for 124 cm and the other one is for 175 cm.
• Hence the distribution is bimodal and modes are 124 cm and 175 cm.

RANGE
• Range is defined by the difference between maximum and minimum value
of the data set.
• This characterizes the variable that it lies in the definable range.
• It is also the measure of dispersion.
• In the example, the minimum height is 120 cm and the maximum height of
the student is 179 cm.
• Hence, the range is the difference of maximum and minimum height which
is equal to (179-150) = 59 cm.

BOXPLOT
• Box plot is always used to describe a data set.
• A simple box-whisker plot is produced using minimum, maximum, 1st quartile,
median, 3rd quartile and range.
• A single box plot is enough to visualize the descriptive statistics of a data set.
• Here a box plot is created for 50 students height.
100
120
140
160
180
Box plot of Students height
Students Height

PERCENTILE
• Percentile is defined as a number at which certain percentage of scores are
lower than that number.
• It does not make sense when it is said that someone has scored 60 out of 75
until the percentile is mentioned (LoBiondo-Wood, Haber & Titler, 2018).
• In the example, percentile values presents a height of which a percentage of
sample falls below.
• Such as, 20% of the students height falls below 127.8 cm.
• 40% of the students height falls below 139 cm.
• 60% of the students height falls below 158.6 cm.
• 80% of the students height falls below 170.2 cm.

STANDARD DEVIATION
• On of the most important measures of dispersion is standard deviation.
• The standard deviation shows the dispersion of the data set from the mean.
• It is nothing but the square root of variance.
• Another way to calculate standard deviation is using formula.
• Formula: f presents the frequency of the data point, N is the summation of the
frequency (Falk, 2018).
• The standard deviation for the height of the students:

REFERENCE
Chatfield, C. (2018). Statistics for technology: a course in applied statistics.
Routledge.
Consoli, S., Recupero, D. R., & Petkovic, M. (2019). Data Science for Healthcare.
Springer International Publishing.
Falk, R. (2018). Understanding probability and statistics: a book of problems. AK
Peters/CRC Press.
LoBiondo-Wood, G., Haber, J., & Titler, M. G. (2018). Evidence-Based Practice for
Nursing and Healthcare Quality Improvement-E-Book. Elsevier Health Sciences.
Solomon, J. A., & Morgan, M. J. (2018). Calculation efficiencies for mean
numerosity. Psychological science, 29(11), 1824-1831.
Stewart, A. (2018). Basic statistics and epidemiology: a practical guide. CRC
Press.

APPENDICES
Below 140 20 Minimum 120
140- Less than 160 10 Maximu 179
Above 160 20 Range 59
Mean 149.06
sum of f.x-square 1130277
Sum (f.x) 7453 sum of f.x 7453
Sum (f)=N 50 N 50
Average 149.06 SD 19.6636
Median 150.5
25th data point 150 20th percentile 127.8
26th data point 151 40th percentile 139
60th percentile 158.6
80th percentile 170.2
Max frequency 3
no. of max freq 2
Mode 124 & 175
Standard deviation
Mean
Frequency
Median
Mode
Range
Percentile
Unique Values (X) Frequency f.x X-square f.X-square
120 2 240 14400 28800
121 1 121 14641 14641
124 3 372 15376 46128
125 1 125 15625 15625
126 1 126 15876 15876
127 2 254 16129 32258
128 2 256 16384 32768
129 1 129 16641 16641
131 1 131 17161 17161
132 1 132 17424 17424
133 1 133 17689 17689
134 2 268 17956 35912
135 1 135 18225 18225
136 1 136 18496 18496
141 1 141 19881 19881
142 1 142 20164 20164
143 1 143 20449 20449
144 1 144 20736 20736
150 1 150 22500 22500
151 2 302 22801 45602
154 1 154 23716 23716
157 2 314 24649 49298
161 2 322 25921 51842
163 1 163 26569 26569
164 2 328 26896 53792
167 1 167 27889 27889
168 1 168 28224 28224
169 1 169 28561 28561
170 2 340 28900 57800
171 2 342 29241 58482
174 2 348 30276 60552
175 3 525 30625 91875
176 1 176 30976 30976
178 1 178 31684 31684
179 1 179 32041 32041