Desklib - Online Library for Study Material with Solved Assignments, Essays, Dissertation

This text includes code snippets related to statistics and data analysis, covering topics such as rent distributions, covariance and independence, convolutions, and Poisson mode. The code is written in MATLAB and includes histograms, probability distributions, and other statistical parameters. The text is related to a homework assignment for a statistics and data analysis course.

HW Assignment 1....................................................................................................................................1
QUESTION 4.............................................................................................................................................1
QUESTION 5.............................................................................................................................................2
QUESTION 6.............................................................................................................................................4
QUESTION 7.............................................................................................................................................5
HW Assignment 1
...Statistics and data Analysis
...@ student Name
...@ student Details
clear
close all
clc
QUESTION 4
... Rent distributions in Randomistan
% Stochastic Heights (SH) and Random Grove (RG)
SHp=12e3;
RGp=18e3;
SH_mean=5100; %RCU
RG_mean=3700; %RCU
rent_median=4000; %RCU
%Plotting histogram
figure(1)
Arent=SHp.*rand(100,1)+RGp.*rand(100,1);
rentdist=Arent;
clmnRent=sum(Arent,1);
edges=min(clmnRent):max(clmnRent)
counts=histc(clmnRent,edges)
RentSum=sum(counts(:))
normalizedOut1=counts/RentSum;
bar(edges,normalizedOut1,'BarWidth',1);
grid on
set(gcf,'name','Rent Distribution','numbertitle','off')
title('Rent Distribution', 'FontSize', 15);
edges =
1.4384e+06

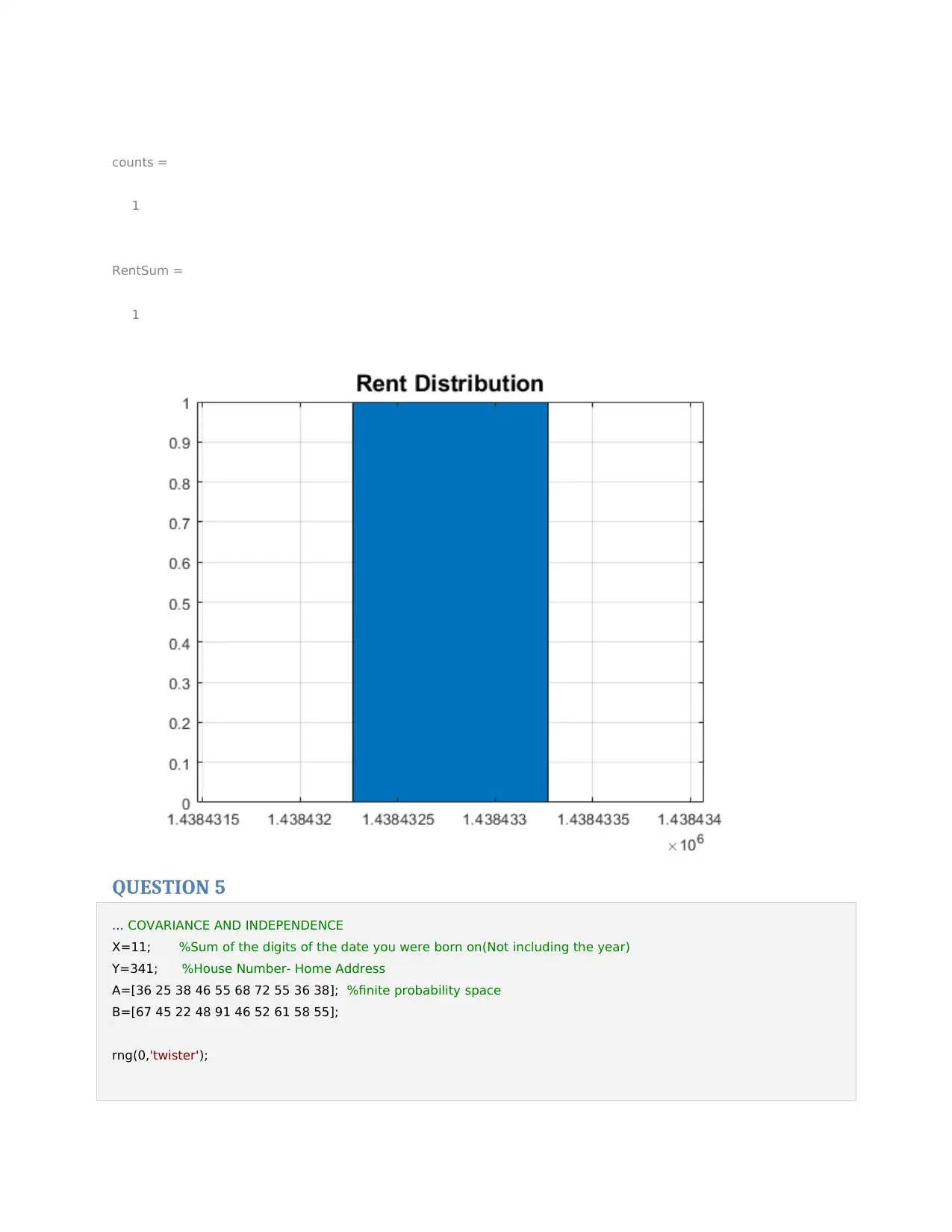
counts =
1
RentSum =
1
QUESTION 5
... COVARIANCE AND INDEPENDENCE
X=11; %Sum of the digits of the date you were born on(Not including the year)
Y=341; %House Number- Home Address
A=[36 25 38 46 55 68 72 55 36 38]; %finite probability space
B=[67 45 22 48 91 46 52 61 58 55];
rng(0,'twister');

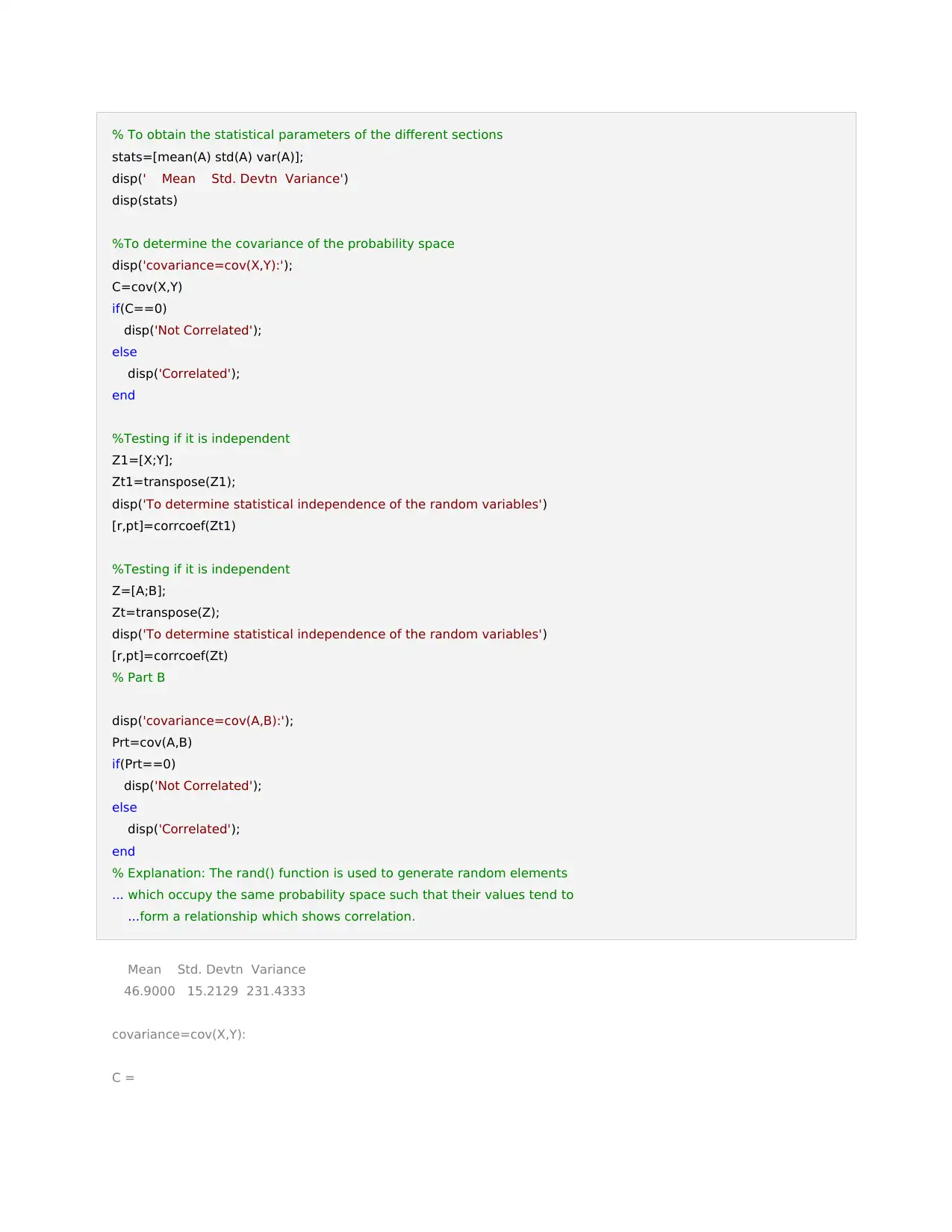
% To obtain the statistical parameters of the different sections
stats=[mean(A) std(A) var(A)];
disp(' Mean Std. Devtn Variance')
disp(stats)
%To determine the covariance of the probability space
disp('covariance=cov(X,Y):');
C=cov(X,Y)
if(C==0)
disp('Not Correlated');
else
disp('Correlated');
end
%Testing if it is independent
Z1=[X;Y];
Zt1=transpose(Z1);
disp('To determine statistical independence of the random variables')
[r,pt]=corrcoef(Zt1)
%Testing if it is independent
Z=[A;B];
Zt=transpose(Z);
disp('To determine statistical independence of the random variables')
[r,pt]=corrcoef(Zt)
% Part B
disp('covariance=cov(A,B):');
Prt=cov(A,B)
if(Prt==0)
disp('Not Correlated');
else
disp('Correlated');
end
% Explanation: The rand() function is used to generate random elements
... which occupy the same probability space such that their values tend to
...form a relationship which shows correlation.
Mean Std. Devtn Variance
46.9000 15.2129 231.4333
covariance=cov(X,Y):
C =

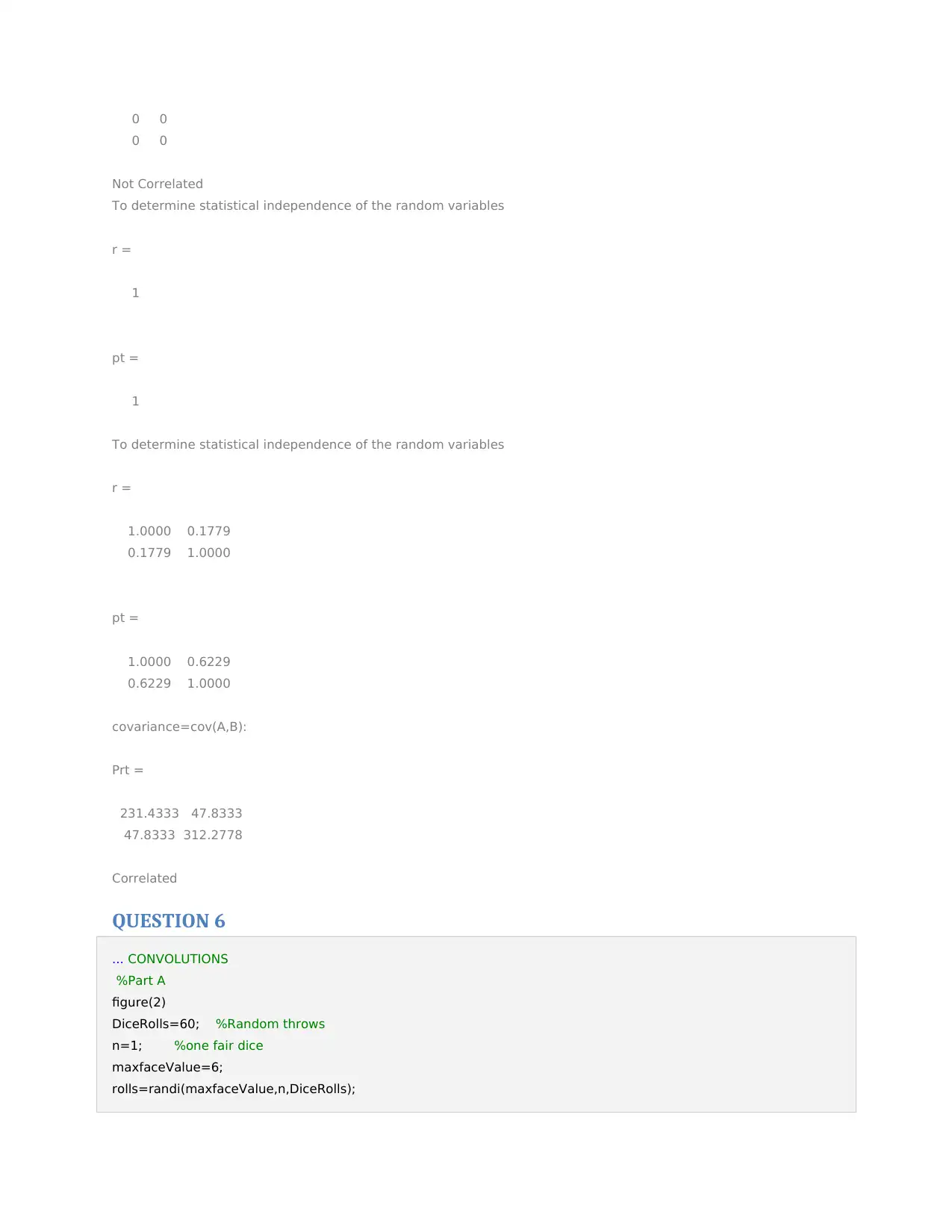
0 0
0 0
Not Correlated
To determine statistical independence of the random variables
r =
1
pt =
1
To determine statistical independence of the random variables
r =
1.0000 0.1779
0.1779 1.0000
pt =
1.0000 0.6229
0.6229 1.0000
covariance=cov(A,B):
Prt =
231.4333 47.8333
47.8333 312.2778
Correlated
QUESTION 6
... CONVOLUTIONS
%Part A
figure(2)
DiceRolls=60; %Random throws
n=1; %one fair dice
maxfaceValue=6;
rolls=randi(maxfaceValue,n,DiceRolls);

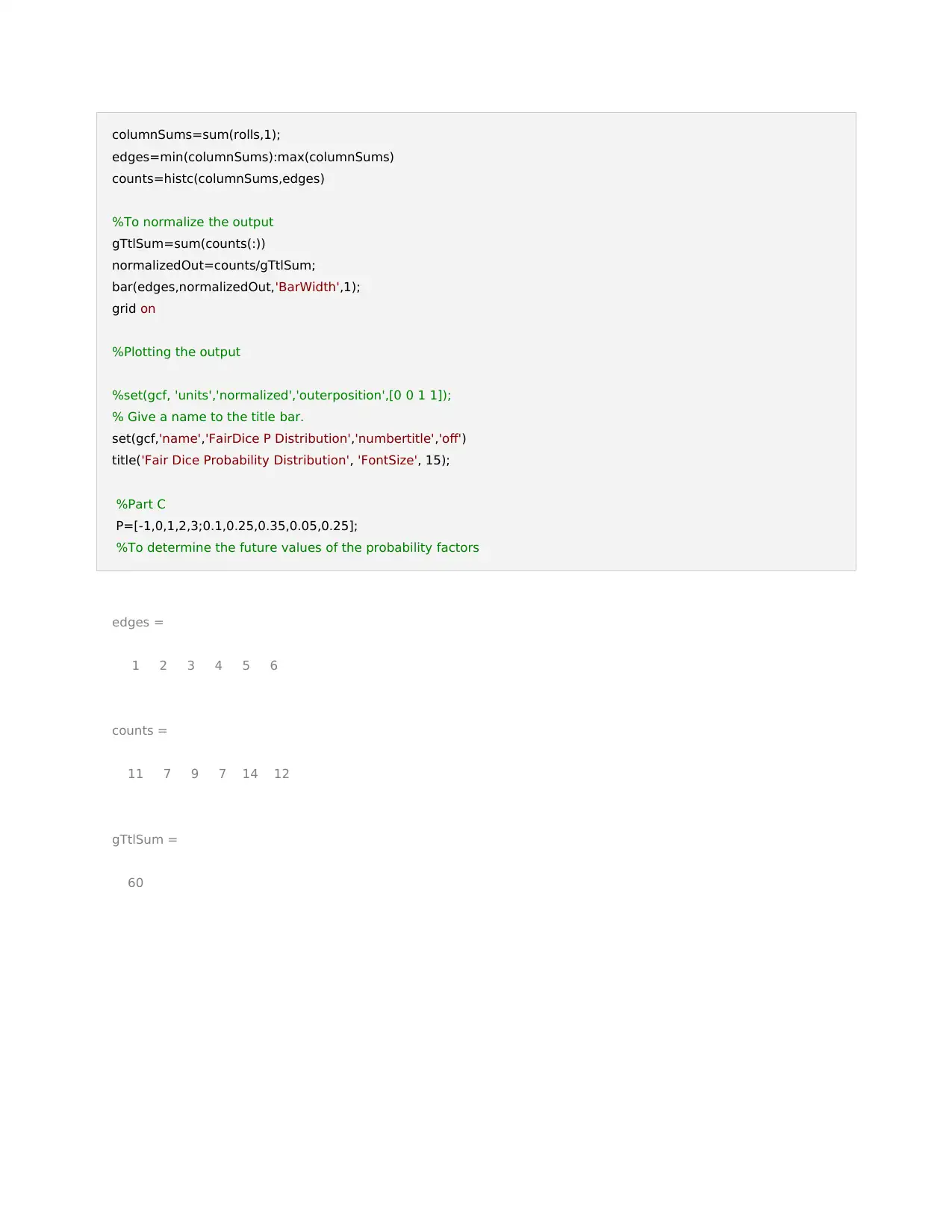
columnSums=sum(rolls,1);
edges=min(columnSums):max(columnSums)
counts=histc(columnSums,edges)
%To normalize the output
gTtlSum=sum(counts(:))
normalizedOut=counts/gTtlSum;
bar(edges,normalizedOut,'BarWidth',1);
grid on
%Plotting the output
%set(gcf, 'units','normalized','outerposition',[0 0 1 1]);
% Give a name to the title bar.
set(gcf,'name','FairDice P Distribution','numbertitle','off')
title('Fair Dice Probability Distribution', 'FontSize', 15);
%Part C
P=[-1,0,1,2,3;0.1,0.25,0.35,0.05,0.25];
%To determine the future values of the probability factors
edges =
1 2 3 4 5 6
counts =
11 7 9 7 14 12
gTtlSum =
60

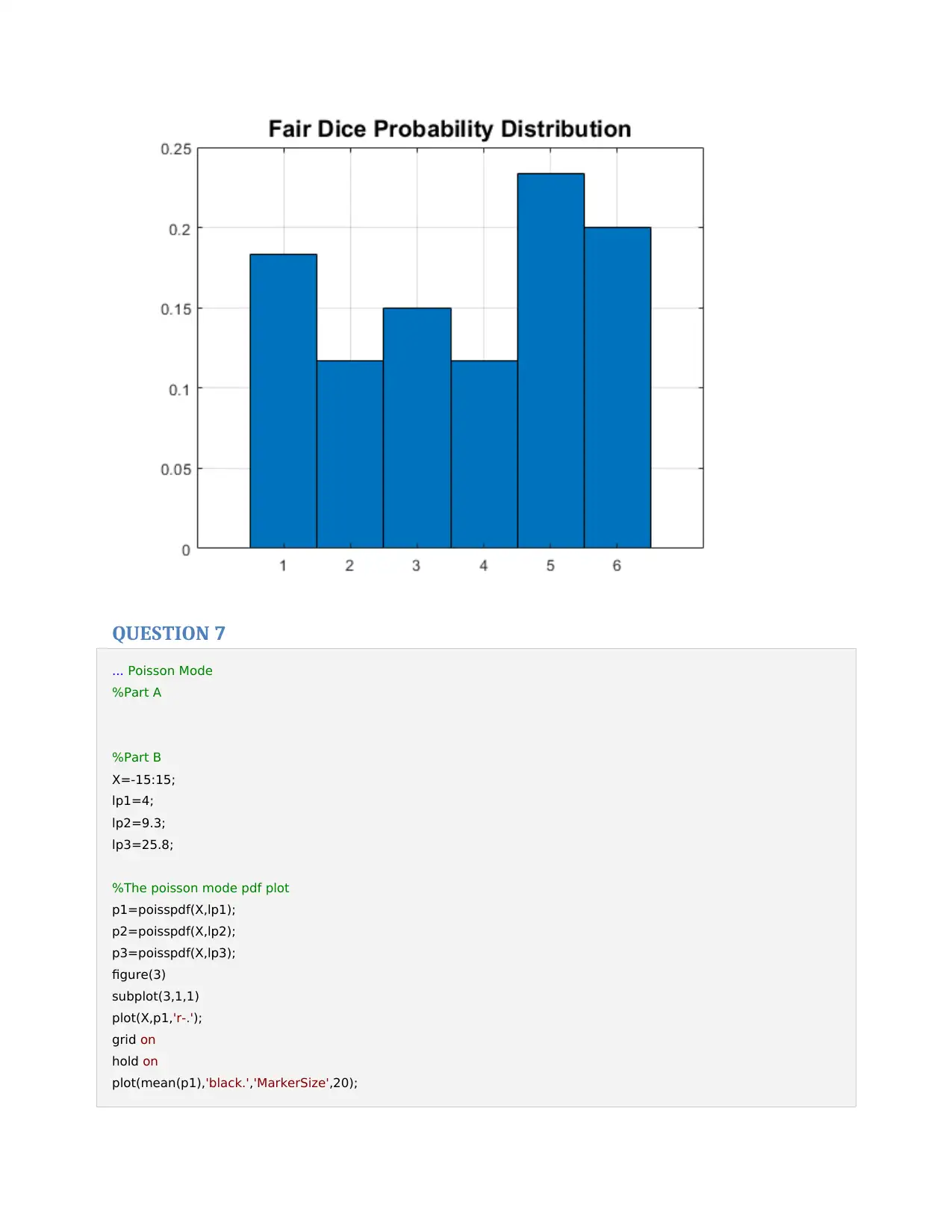
QUESTION 7
... Poisson Mode
%Part A
%Part B
X=-15:15;
lp1=4;
lp2=9.3;
lp3=25.8;
%The poisson mode pdf plot
p1=poisspdf(X,lp1);
p2=poisspdf(X,lp2);
p3=poisspdf(X,lp3);
figure(3)
subplot(3,1,1)
plot(X,p1,'r-.');
grid on
hold on
plot(mean(p1),'black.','MarkerSize',20);

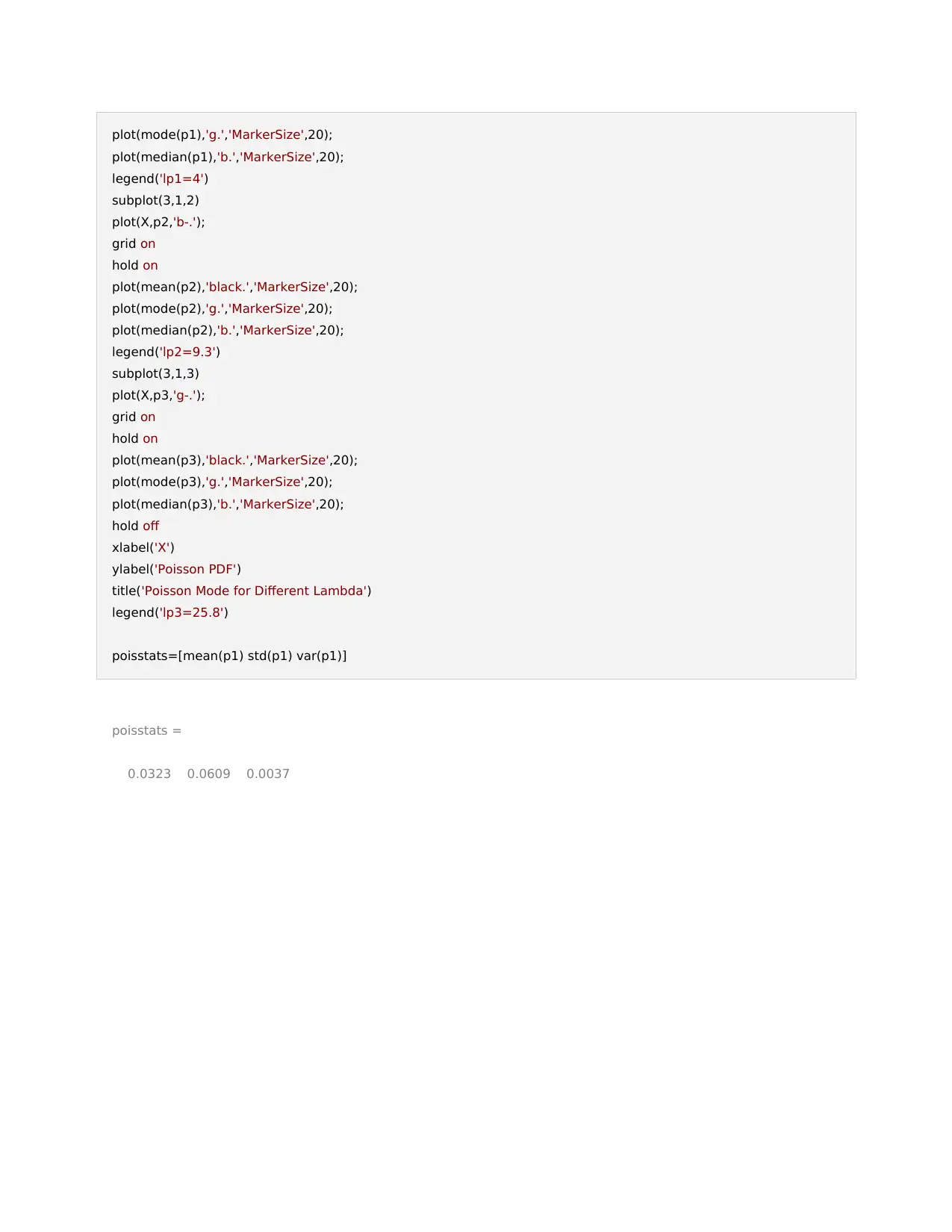
plot(mode(p1),'g.','MarkerSize',20);
plot(median(p1),'b.','MarkerSize',20);
legend('lp1=4')
subplot(3,1,2)
plot(X,p2,'b-.');
grid on
hold on
plot(mean(p2),'black.','MarkerSize',20);
plot(mode(p2),'g.','MarkerSize',20);
plot(median(p2),'b.','MarkerSize',20);
legend('lp2=9.3')
subplot(3,1,3)
plot(X,p3,'g-.');
grid on
hold on
plot(mean(p3),'black.','MarkerSize',20);
plot(mode(p3),'g.','MarkerSize',20);
plot(median(p3),'b.','MarkerSize',20);
hold off
xlabel('X')
ylabel('Poisson PDF')
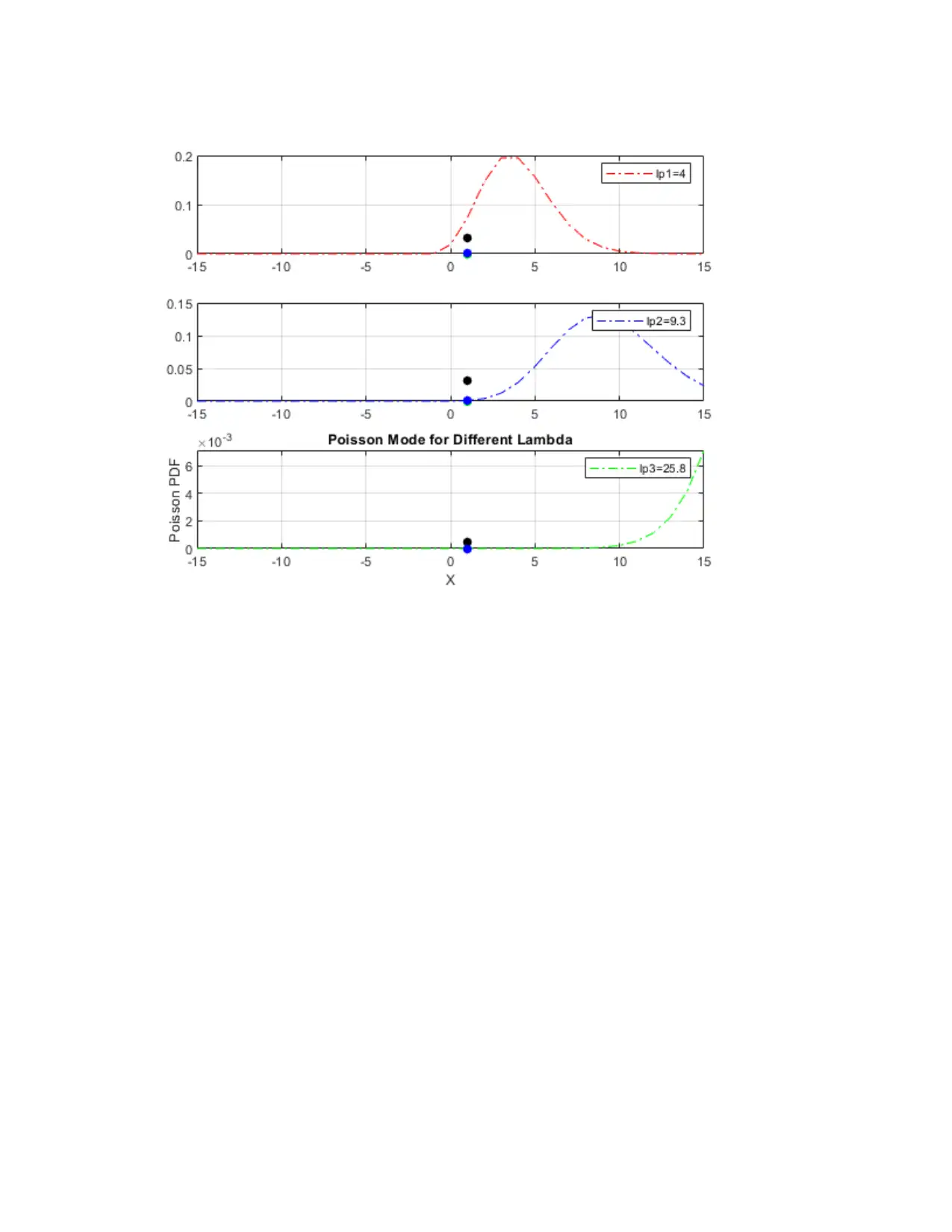
title('Poisson Mode for Different Lambda')
legend('lp3=25.8')
poisstats=[mean(p1) std(p1) var(p1)]
poisstats =
0.0323 0.0609 0.0037