Mathematics Homework: Exponential Decay, Functions, and Calculus
VerifiedAdded on 2023/06/13
|16
|1767
|171
Homework Assignment
AI Summary
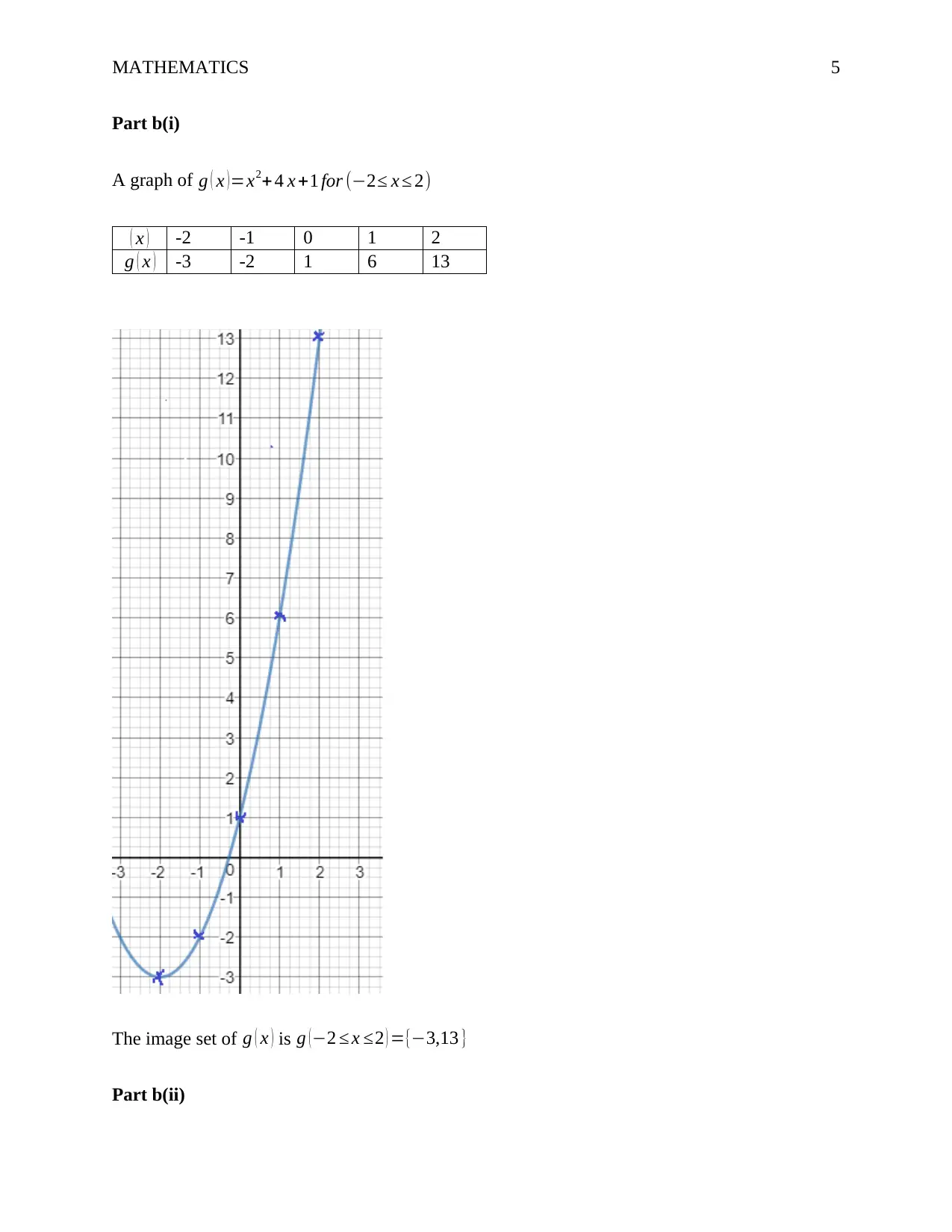
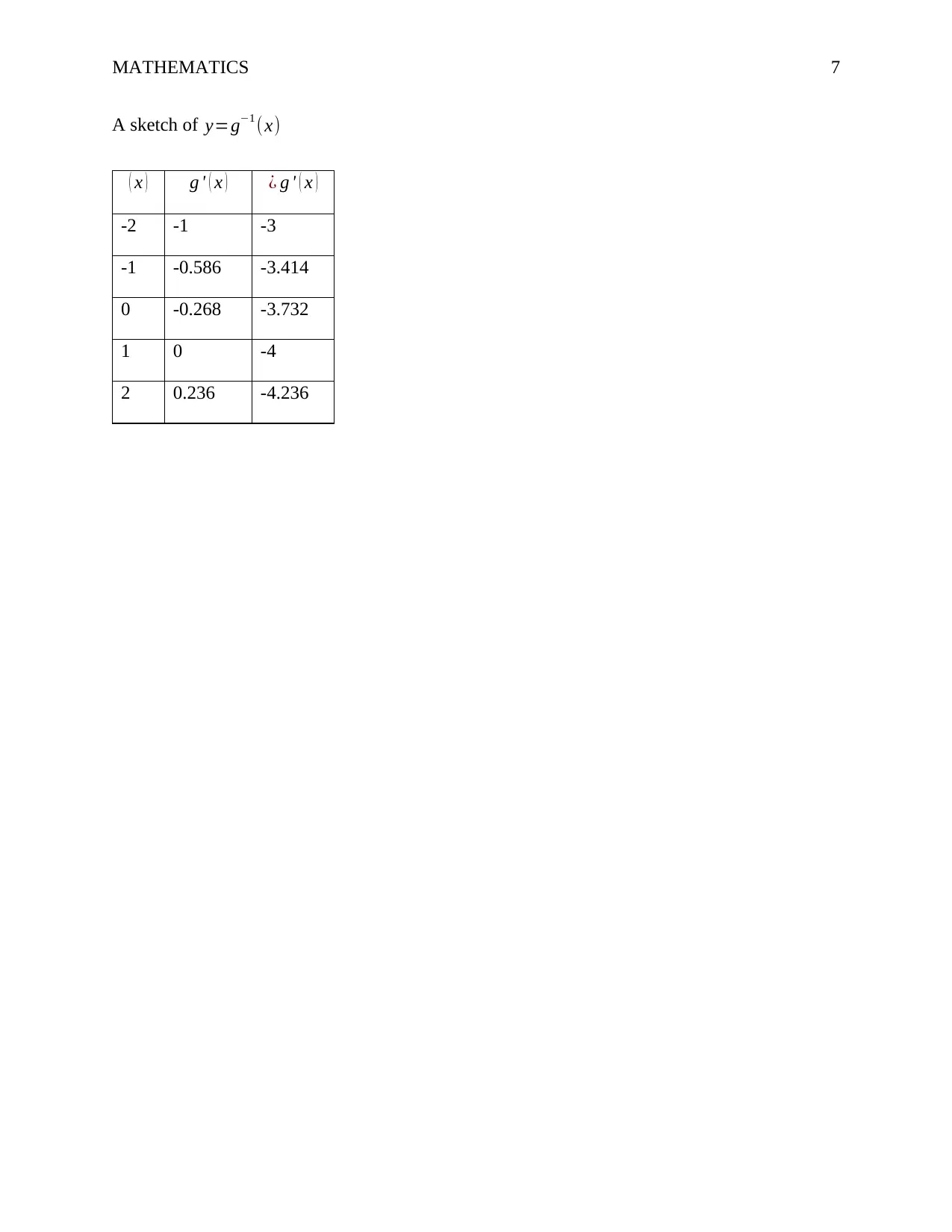
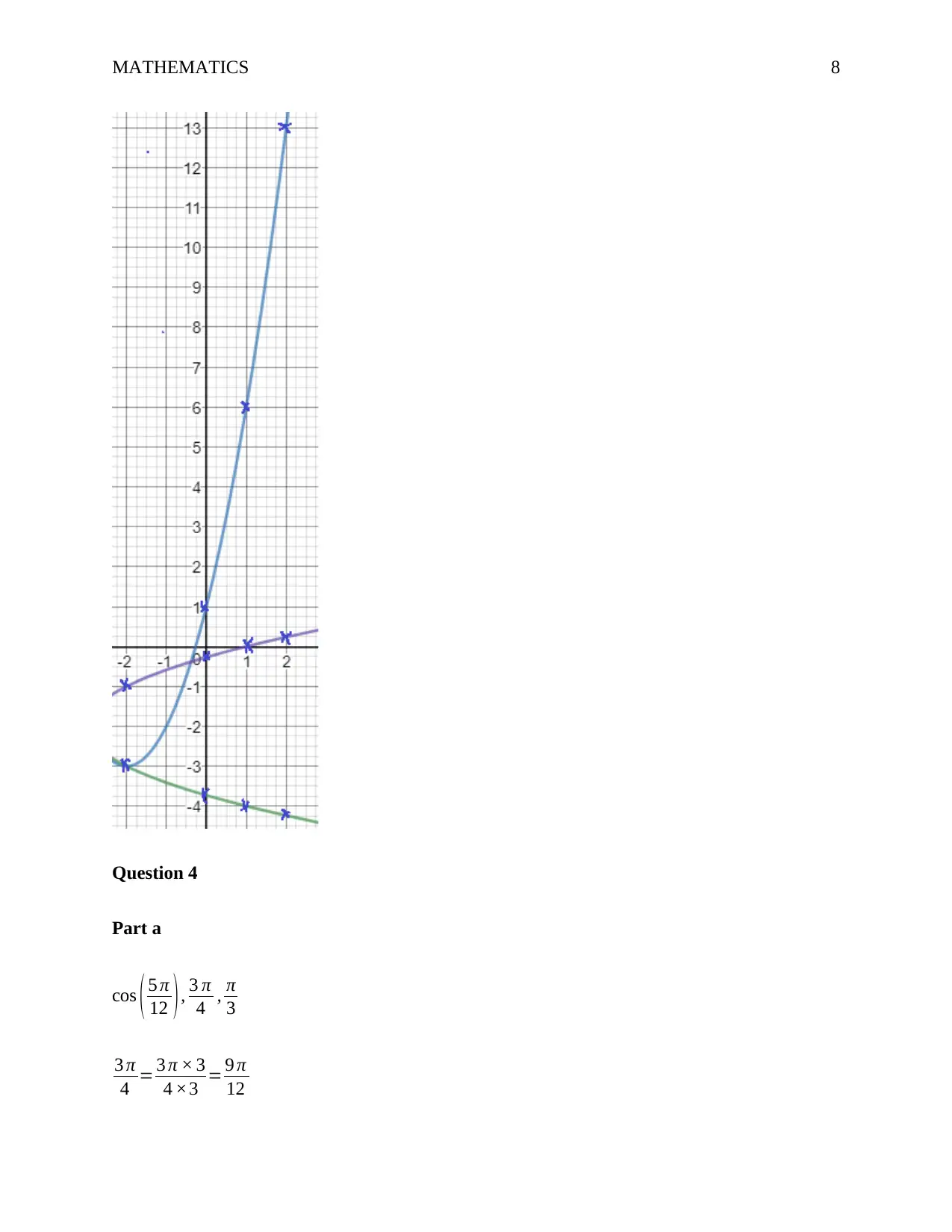
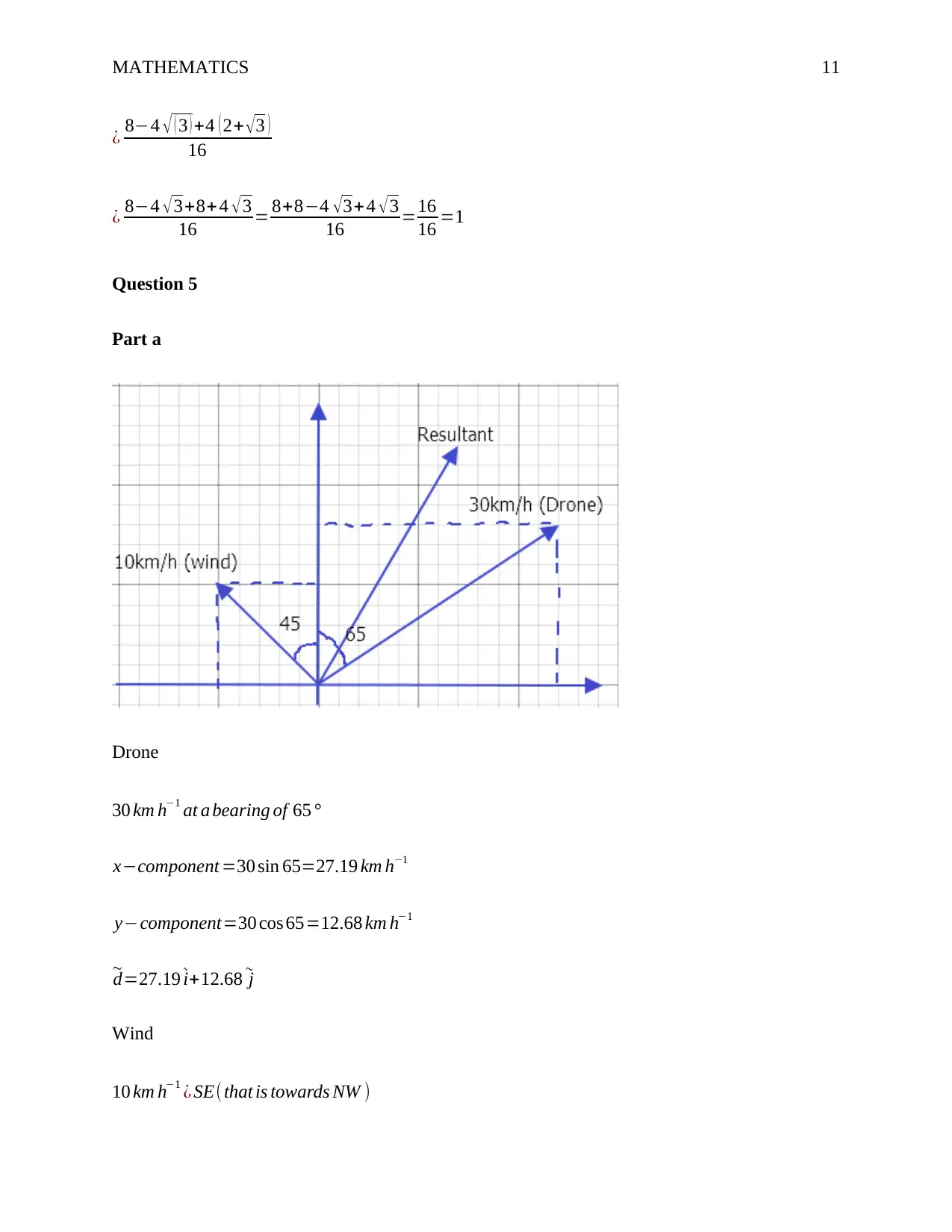
This mathematics assignment provides solutions to several problems, starting with exponential decay modeling the concentration of a banned substance in a racehorse's blood. It determines the constants A and k in the decay function and calculates the time for the concentration to fall below a detectable level. The assignment then solves an inequality using a table of signs and analyzes a quadratic function by completing the square, graphing, and finding its inverse. Further, it involves trigonometric calculations using identities and half-angle formulas. Finally, the assignment tackles a problem involving drone velocity and wind effects, and it finds stationary points of a function, determining whether they are maximum or minimum, and analyzes the motion of a particle using calculus to find velocity and acceleration.
1 out of 16














![[object Object]](/_next/static/media/star-bottom.7253800d.svg)