Determining the Miscibility Diagram for the Methanol-Cyclohexane System

Chemically unreactive liquids act differently when mixed together. The experiment aims to study the miscibility of the binary system of methanol and cyclo-hexane and determine its consolute critical type and composition at their critical point. The results of the experiment agreed with the past studies of the coexistence curve of the methanol and cyclohexane system that exhibited an upper critical solution temperature. The deviation from the provided critical temperature from the literature was only 2% indicating high precision of measurements during the experiment.

DETERMINING THE MISCIBILITY DIAGRAM FOR THE METHANOL-CYCLOHEXANE
SYSTEM. 1
The Determination of the Miscibility of Methanol and Cyclo-hexane System.
[Author Name(s), First M. Last, Omit Titles and Degrees]
[Institutional Affiliation(s)]
Author Note
[Include any grant/funding information and a complete correspondence address.]

the determination of the miscibility of the liquids methanol and cyclo hexane. 2
Abstract
Chemically unreactive liquids act differently when mixed together. Some of these liquids
become miscible to form a homogenous mixture whereas some of the liquids are totally
immiscible and hence form distinct layers of each other based on their densities. However, there
are those liquids that are partially miscible and neither form homogenous mixture nor their
distinct layers.
Keywords: Miscible, immiscible, emulsions, liquids

the determination of the miscibility of the liquids methanol and cyclo hexane. 3
The Determination of the Miscibility of Methanol and Cyclo-hexane System.
According to Stenland & Pettitt (1995), temperature and the composition of two liquids
greatly influences their solubility and for two liquids that are partially soluble, these two phases
of the liquids can be observed. The mutual solubility of these liquids at equilibrium is indicated
by the amounts of each of the liquids in each phase. Depending on the temperatures exposed to
the systems, the systems exhibit different characteristics whereby at high temperatures some
liquids some of the systems become miscible and form one phase uniform mixtures that separate
on lowering the temperatures to form two distinct phases. Such liquids when plotted in a plot of
temperature against mole fraction develop an upper consolute temperature. For the liquids that
become miscible forming one phase uniform mixtures at low temperatures that separate into two
distinct phases at high temperatures end up forming a lower consolute temperature when plotted
in a plot of temperature against mole fraction.
In the experiment, the binary system of the methanol and cyclo-hexane is studied..
According to Jones & Amstell (n.d.), the temperatures before the start of the experiment for both
liquids are recorded to allow for the observation of one phase. The temperatures are then lowered
slowly until the two phases are identified. Curved lines represent the transitions that occur from
the one phase at high temperatures to the two-phase observed at low temperatures. This transition
involves the scattering of light, usually a laser beam. The system will scatter the laser beam upon
approaching the transition temperature. The temperature that is usually recorded is that where
maximum scattering of the laser beam has been observed and is put down as a single point on the
curved line of transition.
The objectives of this experiment were to study the miscibility of the binary system of
methanol and cyclo-hexane and to determine its consolute critical type and to also find out the
composition of the methanol and cyclo-hexane system at their critical point.
Experimental Procedure
The pipetted amounts of both the methanol and cyclo-hexane in a boiling tube were
heated to 50 degrees Celsius in a warm water bathe. Afterwards, the sample was cooled down
slowly until the solution was detected to be cloudy. The solution was heated again until it became
a clear solution. These steps were repeated until a concise cloud point was determined accurately.
The mechanism procedure was repeated for the eight mixtures of the methanol and cyclo-hexane
systems based on their volumes. All the results were recorded.

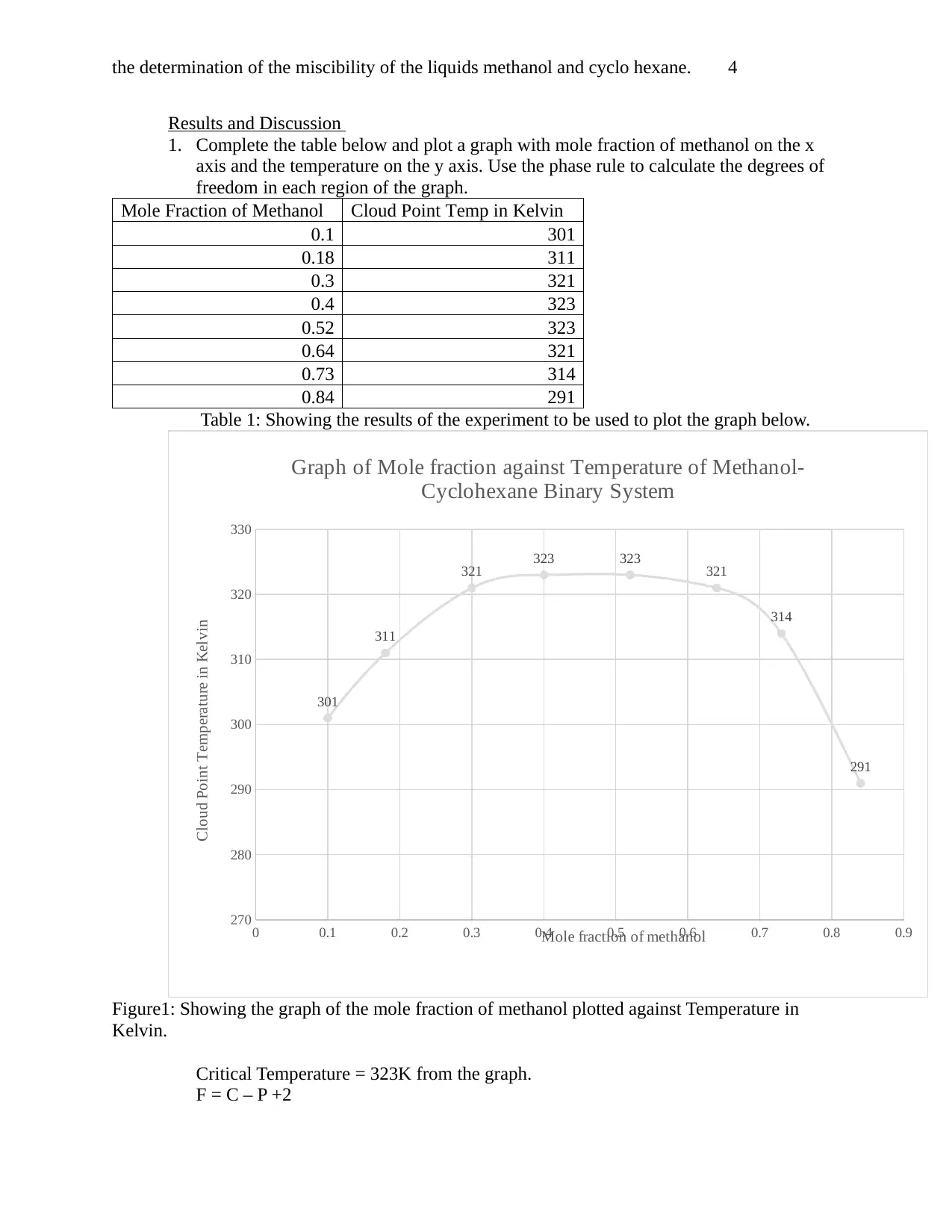
the determination of the miscibility of the liquids methanol and cyclo hexane. 4
Results and Discussion
1. Complete the table below and plot a graph with mole fraction of methanol on the x
axis and the temperature on the y axis. Use the phase rule to calculate the degrees of
freedom in each region of the graph.
Mole Fraction of Methanol Cloud Point Temp in Kelvin
0.1 301
0.18 311
0.3 321
0.4 323
0.52 323
0.64 321
0.73 314
0.84 291
Table 1: Showing the results of the experiment to be used to plot the graph below.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
270
280
290
300
310
320
330
301
311
321 323 323 321
314
291
Graph of Mole fraction against Temperature of Methanol-
Cyclohexane Binary System
Mole fraction of methanol
Cloud Point Temperature in Kelvin
Figure1: Showing the graph of the mole fraction of methanol plotted against Temperature in
Kelvin.
Critical Temperature = 323K from the graph.
F = C – P +2

the determination of the miscibility of the liquids methanol and cyclo hexane. 5
F = 2 – 1 + 2 = 3
P = 1
C = 2
Table 2 below shows the temperature of the observed cloud points as a fraction of
composition
2. The degrees of freedom in each region of the graph are given by the following values
Composition X methanol = 0.4
Composition X cyclohexane = 0.6
Cyclohexane
Volume in ml
Amount per
mol
Methanol
Volume
Amount per
mol
Mole fraction of
methanol
Cloud Point
Temp.
25 0.23 1 0.02 0.1 28
25 0.23 2 0.05 0.18 38
25 0.23 4 0.1 0.3 48
25 0.23 6 0.15 0.4 50
25 0.23 10 0.25 0.52 50
15 0.14 10 0.25 0.64 58
10 0.09 10 0.25 0.73 41
10 0.09 20 0.5 0.84 18
3. Using the given figure as referenced, calculate the % difference between the critical
value determined in the published work and the quoted work above.
The difference in percentage = ( Experiment – Literature Value)
Literature Value × 100
= (323 – 317)
317 × 100
= 2%
4. If a mixture where the mole fraction of methanol was 25% was equilibrated at 290K
it would separate into two phases. Use the figures from your paper and the Lever rule
to calculate the mole fractions of the methanol and cyclohexane in the two-phase
present.
L α CYCLOHEXANE = 0.25 – 0.07 = 0.18
Lβ METHANOL = 0.85 – 0.25 = 0.60
Therefore, L α CYCLOHEXANE = Lβ / (Lβ + L α)
= 0.6 / (0.18 + 0.6)
= 0.77
Lβ METHANOL = L α / (L α + Lβ)
= 0.18 / (0.18 + 0.06)
= 0.23
The experimental data showed that the methanol- cyclohexane system formed one
phase at high temperatures and separated to two-phases on lowering the temperatures
and this was observed by the formation of a cloudy mixture. The results of the
experiment agreed with the past studies of the coexistence curve of the methanol and
cyclohexane system that exhibited an upper critical solution temperature. According
to Arturo, Yanez & Rafael, (2006), this upper critical solution temperature indicated

the determination of the miscibility of the liquids methanol and cyclo hexane. 6
that the methanol and cyclohexane binary system largely depended on the
hydrocarbon`s molecular shapes. This was to mean that the more the branching of the
hydrocarbons mixed with methanol the higher their solubility in the methanol and this
was attributed to the fact that structural branching leads to an increase in the number
of structural isomers. The results obtained from the experiment were therefore done
with very high precision and thus yielded a positive result of the experiment that
agreed with the literature. However, there was a small error observed on the critical
value as compared to the literature value provided in the experiment and this would
be as a result of obtaining the temperatures wrongly and therefore, this caused the 2%
error observed in the critical value point. Besides that, the experiment in general was
a success.
Conclusion.
The miscibility binary system of the methanol and cyclohexane was studied and was
seen to have been affected by the temperatures and composition of the system. This
system was found out to show an upper critical solution temperature which was
recorded at 323 Kelvin. The deviation from the provided critical temperature from the
literature was only 2% indicating high precision of measurements during the
experiment. Lastly, the composition was seen to affect the solubility in that the higher
branching of the cyclohexane resulted in the high solubility observed for the methanol
and cyclohexane binary system that formed a clear solution on dissolving. The
experiment`s objectives were all met and despite the minor error observed in the
experiment, the experiment was a huge success. However, higher precision needs to
be maintained in future works to ensure that the deviation of the critical point from
the literature value does not exceed 1%.
References.
Stenland, C., & Pettitt, B. (1995). Binary- Solution Critical Opalescence.
Journal of Chemical Education. Retrieved from
www.d.umn.edu/psiders/courses/chem4644/2004/BinLiqMix.pdf
Jones, C., &Amstell, S. (n.d.). The Critical Solution Temperature of the System
Methyl Alcohol – Cyclohexane as a means of Detecting and Estimating Water in
Methyl Alcohol. Journal of the Chemical Society (London). Retrieved from
www.d.umn.edu/psiders/courses/chem4644/2004/BinLiqMix.pdf
Arturo, T., Yanez, P., & Rafael, E. (2006). Liquid-Liquid Coexistence Curves
for Binary Systems: Methanol + Cyclohexane and + Several Isomers of Hexane.
Retrieved from, https://pubs.acs.org/doi/abs/10.1021/jeo505321?JournalCode=jceaax

the determination of the miscibility of the liquids methanol and cyclo hexane. 7