Development of mesoscopic computational methods | Boltzmann

DEVELOPMENT OF MESOSCOPIC COMPUTATIONAL METHODS BASED
ON THE BOLTZMAN EQUATION AND THEIR APPLICATION TO
TURBULENT FLOWS, COMPRESSIBLE THERMAL FLOWS, AND
MULTIPHASE FLOWS
By Name
Course
Instructor
Institution
Location
Date

INTRODUCTION
Almost all objects of engineering are immersed in either water or air or both or in their
operations utilize working fluid. This is true particularly for the case of the machines for
conversion as well as generation of energy like for the case of turbines, engines as well as other
renewable devices of energy like wave energy –converters and wind turbines. Modelling such
devices will therefore require much enabling technology in the Chinese engineering field.
(Drikakis, Frank and Tabor, 2019).
Research Background
The primary aim of this study will be to assist in the Development of mesoscopic computational
methods based on the Boltzmann equation and their application to turbulent flows, compressible
thermal flows, and multiphase flows. Computational Fluid Dynamics (CFD) has been identified
as one element which is used in Digital Engineering. Majority of these methods have however
been rendered impractical due to their higher costs of computation in most of the problems. The
method of e lattice Boltzmann (LB) is basically located at the centre of the modelling as well as
simulation hierarchy. The LB is an approach of mesoscopic which is based on the theory of
kinetics as expressed by the original equation of Boltzmann (Nguyen, Wagner and Simon 2019).
Significance of the Study
In some cases there is a minimal form of the equation of Boltzmann in which the principles of
microscopic energy are preserved and are used in the recovery of the hydrodynamic behavior at
the scale considered to be macroscopic. The method of LB is therefore based on the picture of

the particle with the principle aim of predicting the properties of the macroscopic particles. The
nature of the scale- bridging has been considered to be very fundamental as far as the concept of
engineering is concerned in China. The level of technology in the Chinese industries is likely to
improve with the proper understanding of LB concept. In this context, it will allow for the
incorporation of the crucial mesoscopic or microscopic physics while carrying out the recovery
of the laws of the macroscopic as well as characteristics at the computational costs which are
basically affordable (Kaiser et al.2017).
Scope of the work
This particular study was limited to development of mesoscopic computational methods based on
the Boltzmann equation and their application to turbulent flows, compressible thermal flows, and
multiphase flows.
LITERATURE REVIEW
Turbulence Modelling
Turbulence refers to a state of motion of the fluid which has been characterized by tye
occurrence of fluctuations which are random and are of varying scales during the processes o the
flow. In fact the best description has always been the pseudo-random process and its
characterization is done in terms of the individual coherent eddies of various sizes ranging from
largest eddy scale known to be responsible for driving the turbulence down to Kolmogorov
length scale. This determined by the viscosity. The challenge of turbulence modelling usually
constitutes a representation of the fluctuations at random in forms considered to be cheaper. In
other words the processes of making good use of the statistical representations instead of explicit

mechanisms must be adjusted accordingly (Far et al.2016). The flow can therefore be split into
fluctuating as well as mean components so that
u = u- + u’ 0 where u- is some operation for avaraging. Applying this operation of avaraging to
the LB, we find ∂u/ ∂t + ∇.(u/ u) = 1 ρ ∇p + ν∇2u . The term ∇.(u. u) is challenging, but we can
write u u = (u + u ) (u + u 0) = u u + R with R denoting fluctuating and cross-terms, and so ∂u/ ∂t
+ ∇.(u u) + ∇.R = 1 ρ ∇p + ν∇2u (Li et al.2016)
The prominent musicale method will therefore include Lattice-Boltzmann Method (LBM). This
method approaches the problem by an attempt to solve the transport equation of Boltzmann. In
this method, the particles are assumed to be in the lattice and therefore their locations can only be
done at the sites of the lattice. This further confirms that the movement of the particles can only
be traced to the nearest vortex (Geier, Pasquali, and Schönherr 2017). The velocities will
therefore be restricted to the directions of lattice with a representations of s c ∈ {0, 1} d , in
which d refers to the lattice vectors number.
Multiphase flows
In the case of the multiphase flows, the method of pseudopotential LB as well as the method of
phase-field LB have been very sucessful and become popular in most of the sections. They have
been taken through varios stages of development and applied in the study of various concepts of
dynamics of the flows which experience wide ranges at ratios considered to be of realistic
densities, Weber numbers and Reynolds numbers. The governing equation this becomes ;

in which
where relaxation time is the τh (Kutscher, Geier and Krafczyk 2019).
compressible thermal flows
In the case of the compressible thermal flows, the approaches of the LB on the standards of
lattices. The simlified models of the LB have practically indicated errors in the simp;lified
concepts which are energy-based. The indicated errors are in terms of the macroscopic
equations. In this thermal LB model, the focus should be on the cortrect recovery of the
requiered or target values of tenmperatures. This goes alongside the equations of energy.
(Li et al.2016).

METHODOLOGY
The research will use both the collected experimental data and scholarly articles to meet its
objectives. Schematic Illustrations of Research Methodology
Introductio
n
Literature Review
Methodology
Conclusion and Recommendations
Results and Discussions
Mesoscopic
computational methods
Aims & Objectives
Size shape in
Compressive tests Resources:
 Journals
 Research articles
 Books
 Reports
Project Rationale
Experimental
Investigation
Benefits
Research Gap
ApplicationsPerformanc
e Measure
of of

CONCLUSION
The study has an objective of exploring the development of mesoscopic computational methods
based on the Boltzmann equation and their application to turbulent flows, compressible thermal
flows, and multiphase flows (Meng and Guo 2016). The Boltzmann equation has been
identified to be very fundamental as far as the selected three types of the flow are concerned. The
study will be enhanced at various levels by the use of the various experimental data and scholarly
articles. This particular study will be expected to run for a period of eight months so that it can
effectively realize its objective.
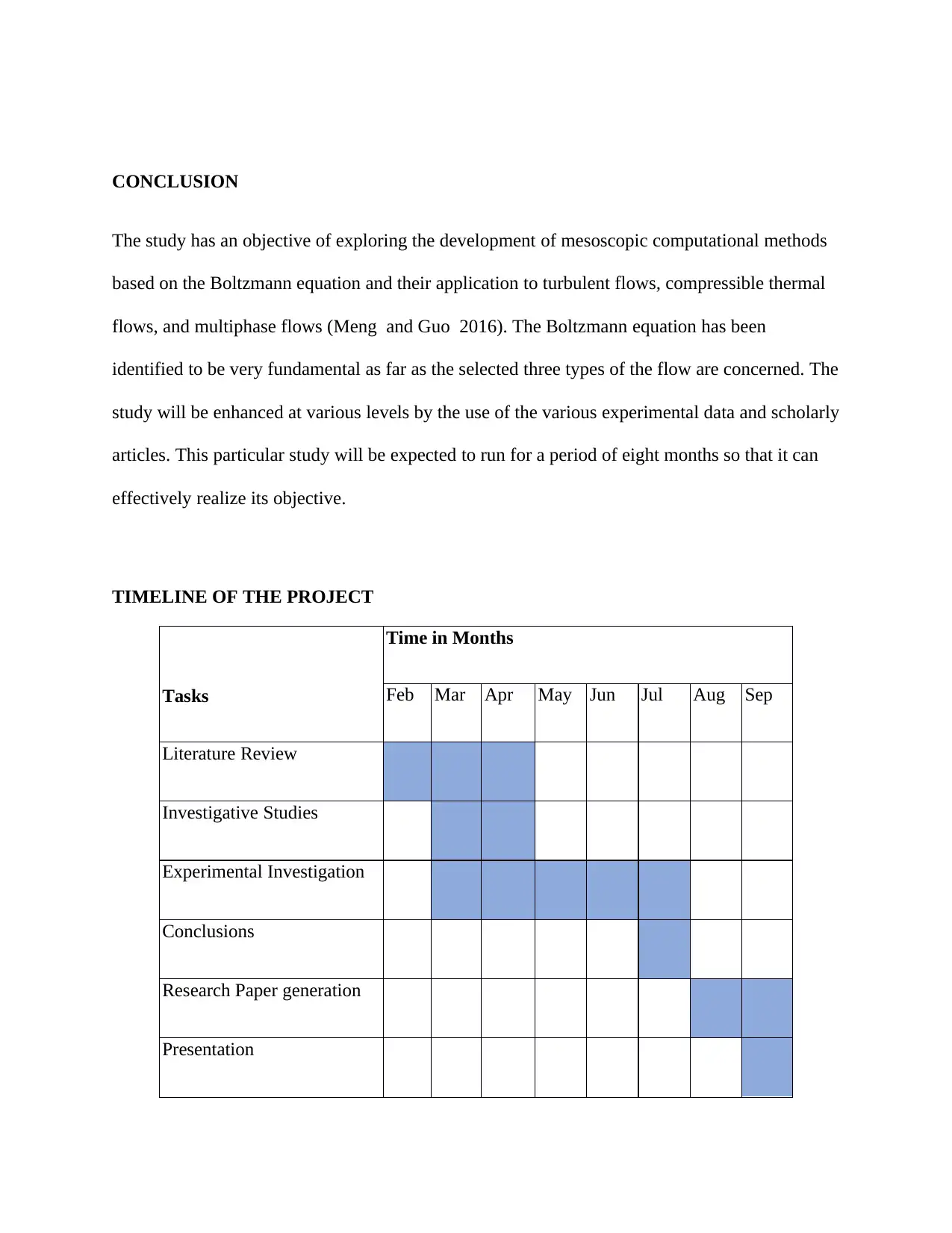
TIMELINE OF THE PROJECT
Tasks
Time in Months
Feb Mar Apr May Jun Jul Aug Sep
Literature Review
Investigative Studies
Experimental Investigation
Conclusions
Research Paper generation
Presentation

REFERENCES
Drikakis, D., Frank, M. and Tabor, G., 2019. Multiscale computational fluid
dynamics. Energies, 12(17), p.3272.
Far, E.K., Geier, M., Kutscher, K. and Krafczyk, M., 2016. Simulation of micro aggregate
breakage in turbulent flows by the cumulant lattice Boltzmann method. Computers &
Fluids, 140, pp.222-231.
Geier, M., Pasquali, A. and Schönherr, M., 2017. Parametrization of the cumulant lattice
Boltzmann method for fourth order accurate diffusion Part II: Application to flow around a
sphere at drag crisis. Journal of Computational Physics, 348, pp.889-898.
Kaiser, J., Feng, T., Maassen, J., Wang, X., Ruan, X. and Lundstrom, M., 2017. Thermal
transport at the nanoscale: A Fourier's law vs. phonon Boltzmann equation study. Journal of
Applied Physics, 121(4), p.044302.
Kutscher, K., Geier, M. and Krafczyk, M., 2019. Multiscale simulation of turbulent flow
interacting with porous media based on a massively parallel implementation of the cumulant
lattice Boltzmann method. Computers & Fluids, 193, p.103733.
Li, Q., Luo, K.H., Kang, Q.J., He, Y.L., Chen, Q. and Liu, Q., 2016. Lattice Boltzmann methods
for multiphase flow and phase-change heat transfer. Progress in Energy and Combustion
Science, 52, pp.62-105.

Meng, X. and Guo, Z., 2016. Localized lattice Boltzmann equation model for simulating
miscible viscous displacement in porous media. International Journal of Heat and Mass
Transfer, 100, pp.767-778.
Nguyen, D.X., Wagner, G. and Simon, S.H., 2019. Quantum Boltzmann equation for bilayer
graphene. arXiv preprint arXiv:1901.07039.