Discovering Mathematics: MU123 EMA

The assignment provided covers a range of mathematics and statistics problems, including linear models, exponential functions, and statistical analysis. It involves solving questions on topics such as Discovering Mathematics MU123 EMA, number of games sold to date, and determining the value of s-intercept. The student is required to demonstrate their understanding of mathematical concepts and apply them to real-world scenarios.

DISCOVERING
MATHEMATICS
MU123 EMA
Student Name
[Pick the date]

Question 1
One change that I intend to make in my study plan in the future would be to practice the concepts
learnt in class on the very same day. This is because in the class, there were a number of topics
which seemed qutie straight forward but I faced significant problems when I did the same some
days later. Hence, in order to avoid this problem and to enhance learning, I would like to rectify
this error the next time around.
Question 2
Katie’s and Rebecca’s number of steps over a period of two week is highlighted below:
(a) (i) The respective numerical summary is shown below:
(ii) The given data is discrete data since the data cannot be in decimals.
1

(iii) The two measures of location to decide who has higher number of steps on average are
“Median and Mean.” Based on the above table, it can be seen that mean and median are higher
for Rebecca and therefore, Rebecca has greater number of steps on average.
(iv) The measures of spread to decide who has higher variability in terms of number of steps are
“Standard deviation, Inter-quartile range, Range.” All the three measures are higher for Rebecca.
Therefore, Rebecca’s number of steps is higher than Katie’s number of steps.
(b) (i) Boxplots
 Boxplot for variable Katie’s number of steps over two week period
 Boxplot for variable Rebecca’s number of steps over two week period
2

(ii) The box plot for Rebecca is clearly asymmetric as highlighted from the unequal distance
between Q1 and median & median and Q3. This implies that the spread of the data would be
more and also there would be potential presence of outliers in the data.
(iii) (1) This claim is false since from the box-plot of Katie, it is apparent that Q3 or 75th
percentile for the given data fall is 10.753 steps.
(2) This statement is false since the 8946 is marginally greater than the median of 8945.5 steps
which clearly implies that days when Katie did more than 8946 would be less than 50% while
days when she did less than 8946 steps would be slightly in excess of 50%.
(c) Running data over three weeks are highlighted below:
3

Based on the maximum running distance covered by Daniel and Andrew, it can be seen that
maximum running distance covered by Daniel is 8678 meter. In figure A, the maximum distance
cover of 8678 is possible and hence, figure A is the histogram represents the running distance
covered by Daniel. In figure B, the maximum distance is in excess of 10,000 steps.
Question 3
(a) Straight line passes through (1, -1) and (-2, 8)
(i) Gradient of the line
m= 8− (−1 )
−2− ( 1 ) = 9
−3 =−3
(ii) Equation of line
¿
y +1=−3 x +3
y=−3 x +2
4

(iii) The value of x-intercept
Value of x intercept would be at y = 0.
0=−3 x+ 2
x= 2
3 =0.667
(b) Point (3, -11) lie on the straight line =?
If the point satisfies the equation then the point lies on the line.
y=−3 x +2
LHS
y=−11
RHS
¿− ( 3∗3 ) +2=−7
The point (3, -11) does not lie on the line.
(c) Coordinates of point where the lines intersect.
9 x− y =2
−6 x +4 y=7
Here,
9 x− y =2
x= 2+ y
9
5

Put in equation 2
−6 x +4 y=7
−6 ( 2+ y
9 )+ 4 y =7
y= 5
2
Hence,
x=
2+( 5
2 )
9 = 1
2
Therefore, the point at which the lines would intersect is ( 1
2 , 5
2 ).
(d) Equation of parabola
y=−0.15 x2 + x +0.5
(i) The value of y-intercept
y=0.5
The value of y –intercept is 0.5.
(ii) (1) Coordinates of point where line x = 4 meets the parabola
y=−0.15 x2 + x +0.5
y=−0.15(4)2+ 4+0.5
6

y=2.1
Coordinates of point where line x = 4 meets the parabola is (4, 2.1).
(2) From the above, it is apparent that the y coordinate is 2.1m and hence the water would flow
above the sculpture with a height of 1.8m which is placed at the horizontal distance of 4 m from
the fountain.
(iii) (1) The value of x-intercept
y=−0.15 x2 + x +0.5
The value of x –intercept at which y=0.
0=−0.15 x2+ x +0.5
−0.15 x2+ x +0.5=0
−15 x2+100 x +50=0
x=−100 ± √(100)2−4 ( −15 )∗50
2∗(−15)
x=− √130+10
3 , 10+ √130
3
The value of x –intercept is (− √13010
3 , 10+ √130
3 ).
(2) Requisite distance = 10+ √130
3
Question 4
(a) (i) x−5=4 x +10
7

x−4 x=10+5
−3 x=15
x= 15
−3 =−5
(ii) 12−2 ( x+ 3
4 )=3
2 x
12−2 x− 3
2 = 3
2 x
−2 x−3
2 x=−21
2
−7
2 x=−21
2
x=3
(iii) 3 x
x−5 + 1
x +1 =3
3 x ( x+ 1 )+1 ( x−5 )
( x−5 ) ( x +1 ) =3
3 x2 +3 x+ x−5
x2 +x−5 x−5 =3
3 x2 +4 x−5
x2−4 x−5 =3
3 x2+4 x−5=3 ( x2−4 x −5 )
3 x2+4 x−5=3 x2 −12 x−15
8

16 x=−10
x=−5
8
(b) Factors and solution of equation
2 x2 +4 x−70=0
Factors
¿ 2 ( x2+2 x−35 )
¿ 2 { x2+ ( 7 x−5 x ) −35 }
¿ 2 ( x2+7 x−5 x−35 )
¿ 2 { x ( x +7 ) −5 ( x +7 ) }
¿ 2(x +7)( x−5)
Hence, the factors of the equation is 2 ( x+7 ) ( x−5 ) .
Solution of equation
2 x2 +4 x−70=0
2 ( x+7 ) ( x−5 )=0
x +7=0 , x=−7
x−5=0 , x=5
Solution of the equation is 5, -7.
(c) (i) Rearrange in terms of b subject
2 a=b−c (b
3 −4 )
9

2 a=b−c (b−12
3 )
2 a=b− ( bc−12 c
3 )
2 a=3 b−bc +12 c
3
6 a=3 b−bc+ 12c
6 a−12 c=b ( 3−c )
b= 6 a−12 c
( 3−c )
(ii) The two mistakes are highlighted below:
Question 5
The figure is shown below:
10

(a) (i) Length of BC
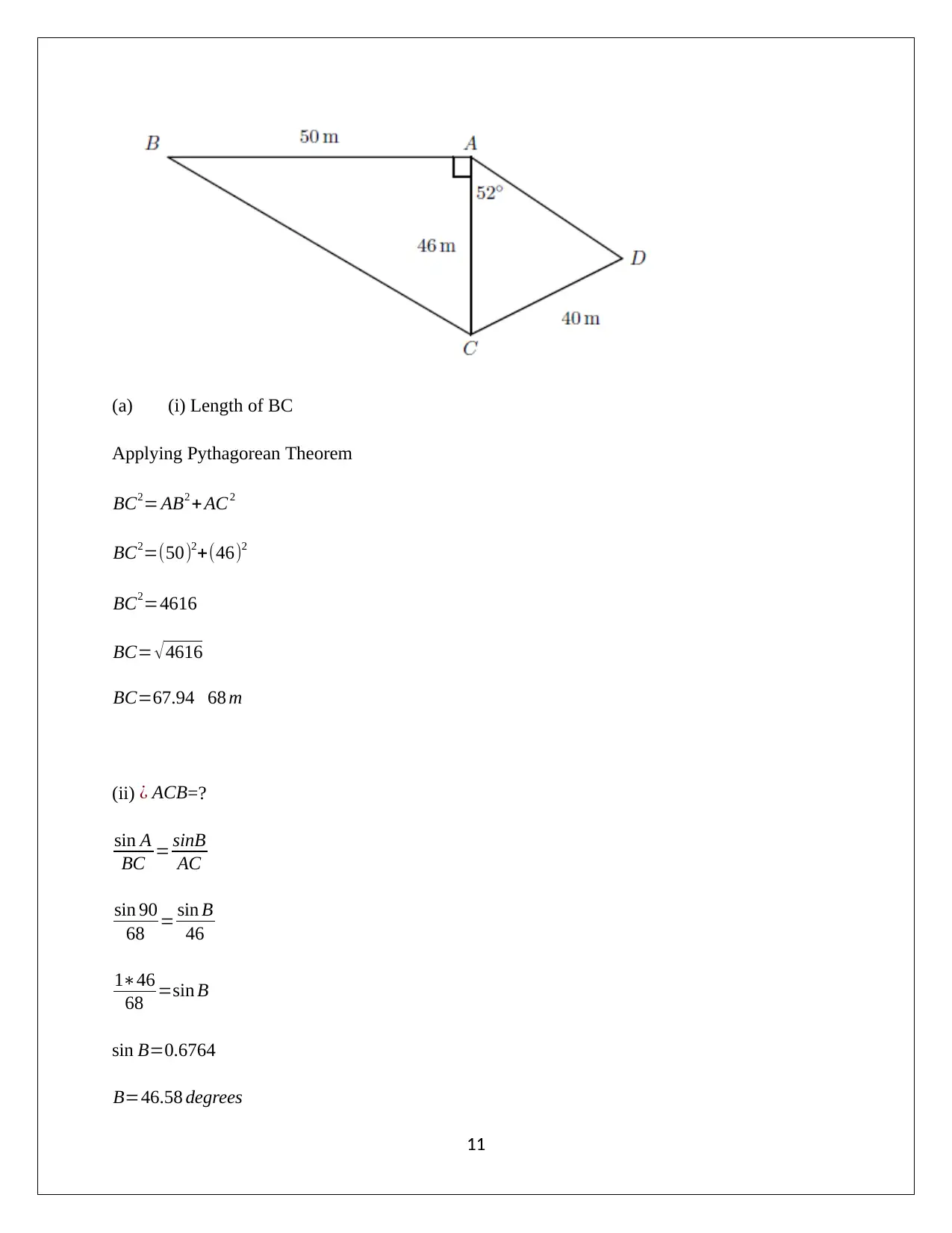
Applying Pythagorean Theorem
BC2= AB2 +AC 2
BC2=(50)2+(46)2
BC2=4616
BC= √4616
BC=67.94 68 m
(ii) ¿ ACB=?
sin A
BC = sinB
AC
sin 90
68 = sin B
46
1∗46
68 =sin B
sin B=0.6764
B=46.58 degrees
11

Thus,
¿ A+¿ B+¿ C=180
90+46.58+C=180
C=43.41 degrees
Hence,
¿ ACB=43.41 °
(b) ¿ ADC is ´¿
In triangle ACD
sin A
CD = sinD
AC
sin 52
40 = sinD
46
sin D=0.8383
D=63.29°
Hence, ¿ ADC is 63.29°
(ii) Cosine rule to determine length AD
¿ C=180−52−63.29=64.71
c2=a2+ d2−2 ad cos C
c2=(40)2 +(46)2−(2∗40∗46)cos 64.71
c2=1778.9
12

c=42.2
Hence, the length of AD is 42.2 m.
(c) Inside radius = 30m
Outside radius = 31 m
(i) Circumference of the inside of wheel ¿ 2 π Ri
Circumference=2 π∗30=188.4 m
(ii) Area of the painted part ¿ π R0
2−π Ri
2
Area=π (31)2−π ( 30 )2=191.64 m2
(d) (i) Length corresponding to AB on the photo = 50-2*(0.04) = 49.92 m
(ii) The angle CAB would continue to remain 900 as owing to the painting wheel there would
be adjustment on the both sides which would imply that the overall angle would remain the
same as before.
Question 6
(a) Total number of games sold to date is a linear model and is highlighted below:
s=2000 ( t−20 ) + 220,000(t ≥ 20)
(i) Number of sales after 24 weeks
t=24
s=2000 ( 24−20 )+220,000
13

s=228,000
Therefore, the number of sales after 24 weeks is 228,000.
(ii) Number of weeks for which the sales would be 230,000
s=230,000
230,000=2000 ( t −20 )+ 220,000
10,000=2000 ( t−20 )
5=t−20
t=25
(iii) Gradient of the line needs to be determined
s=2000 ( t−20 )+ 220,000
s=2000t−40,000+220,000
s=2000t +180,000
Compare with y=mx+c
The gradient of the straight line is 2000.
For increase of one week the number of sales would increase with a factor of 2000.
(iv) The value of s – intercept is a value at which t = 0,
s=2000t +180,000
At t = 0
14

s=180,000
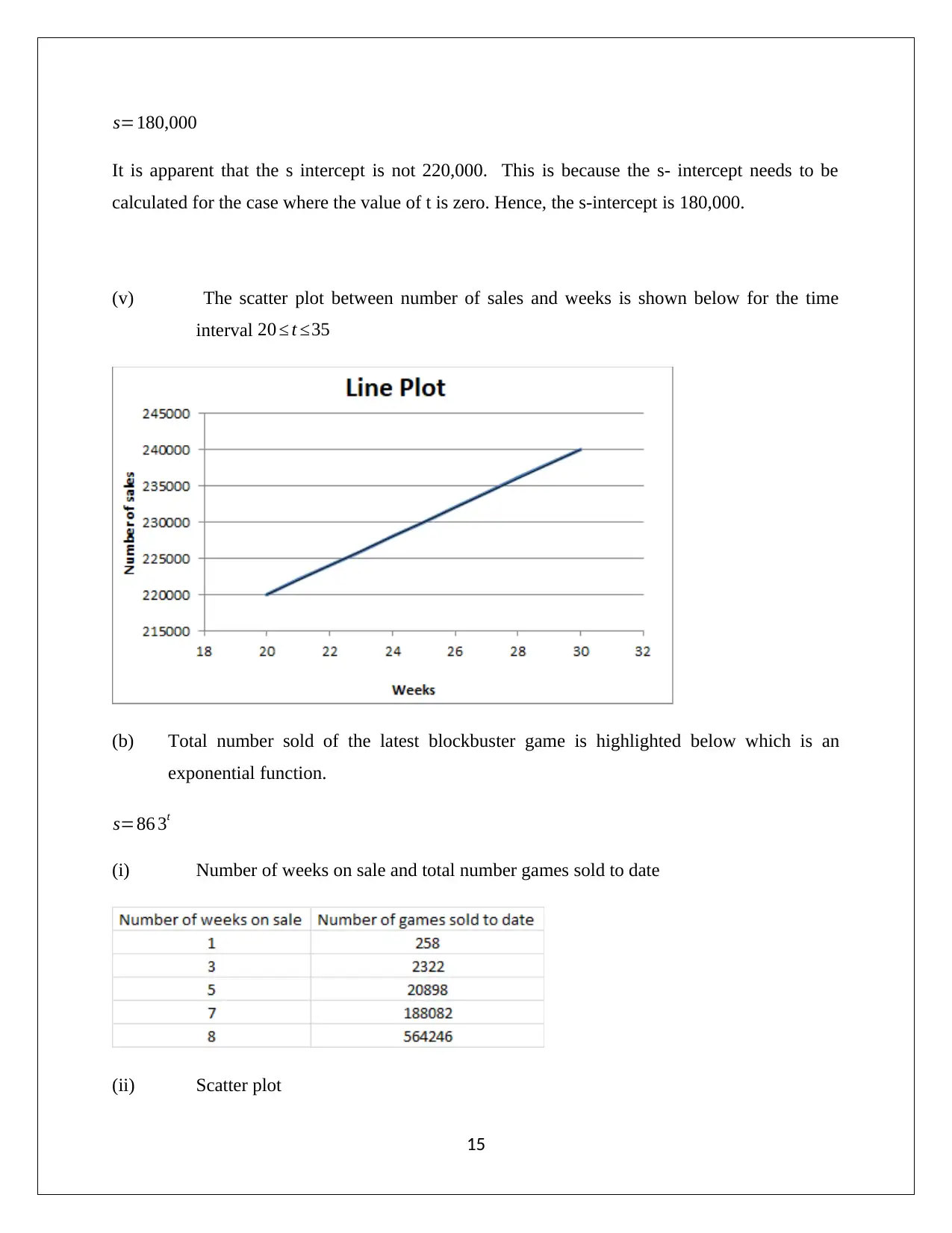
It is apparent that the s intercept is not 220,000. This is because the s- intercept needs to be
calculated for the case where the value of t is zero. Hence, the s-intercept is 180,000.
(v) The scatter plot between number of sales and weeks is shown below for the time
interval 20 ≤ t ≤35
(b) Total number sold of the latest blockbuster game is highlighted below which is an
exponential function.
s=86 3t
(i) Number of weeks on sale and total number games sold to date
(ii) Scatter plot
15

(iii) Number of weeks on sale =?
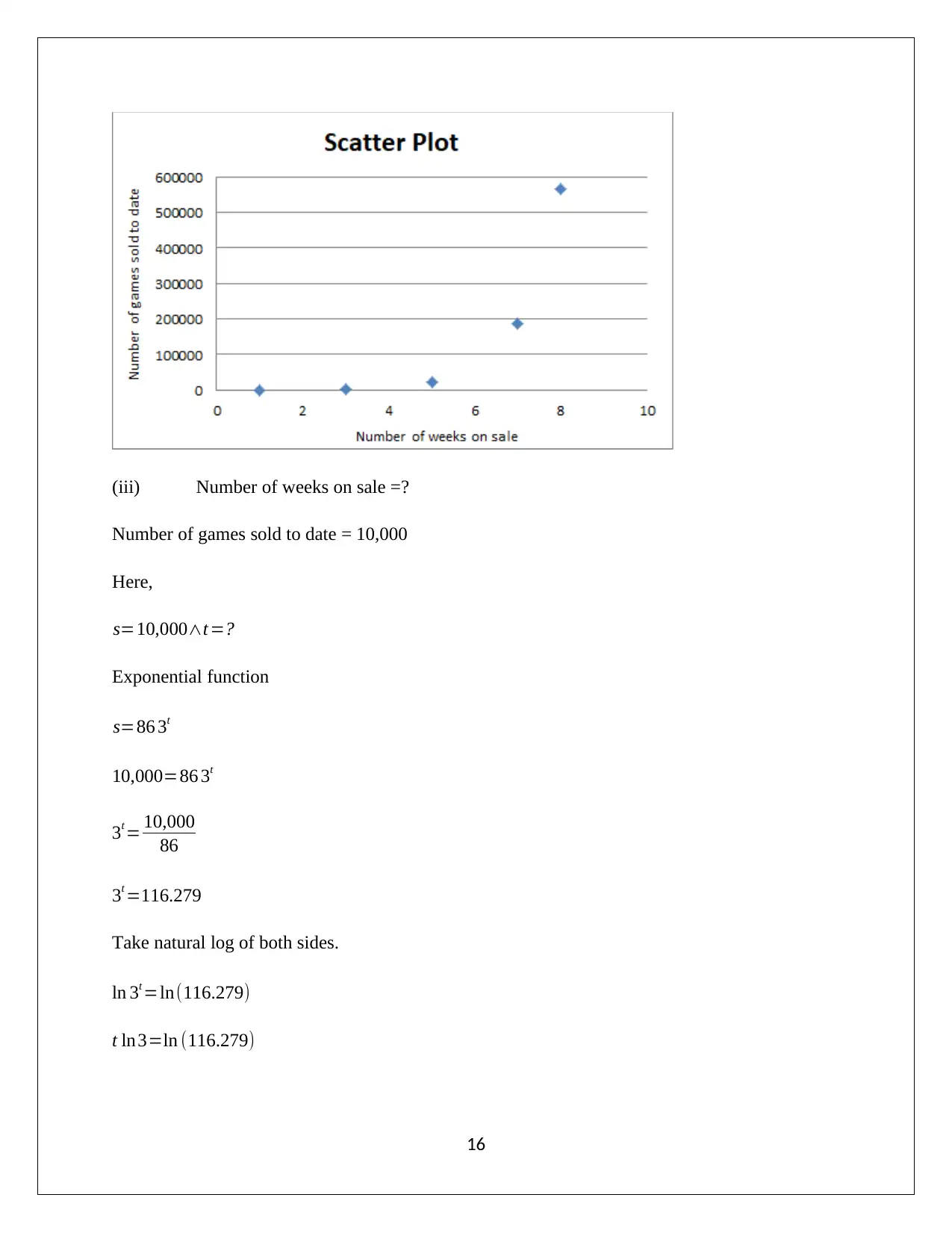
Number of games sold to date = 10,000
Here,
s=10,000∧t=?
Exponential function
s=86 3t
10,000=86 3t
3t = 10,000
86
3t =116.279
Take natural log of both sides.
ln 3t =ln(116.279)
t ln3=ln (116.279)
16

t= ln ( 116.279 )
ln 3
t=4.32909
Therefore, the number of weeks would be 4.3 in order to get the number of sales 10,000.
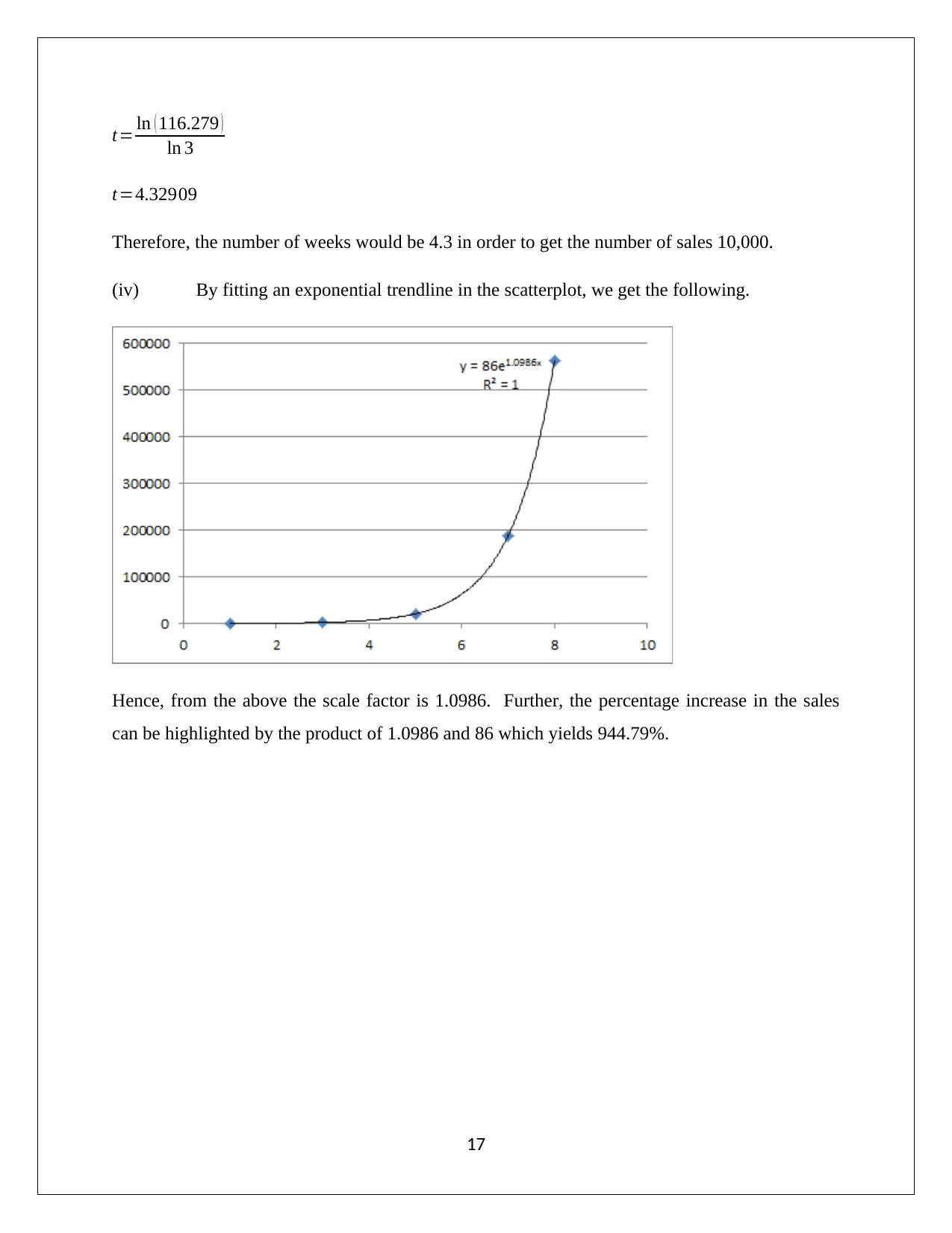
(iv) By fitting an exponential trendline in the scatterplot, we get the following.
Hence, from the above the scale factor is 1.0986. Further, the percentage increase in the sales
can be highlighted by the product of 1.0986 and 86 which yields 944.79%.
17