Discrete Mathematics: Equivalence Relations, Partial Orders and Groups

This document presents a solved assignment in Discrete Mathematics, focusing on fundamental concepts such as equivalence relations, partial orders, and group theory. The solution begins by determining the smallest equivalence relation on a given set, followed by identifying equivalence classes. It then constructs a Hasse diagram for a partial order defined on a set of integers and identifies the largest sets of mutually comparable and non-comparable elements. The assignment further delves into group theory, proving that a given set of bijections forms a subgroup of S4 using a Cayley table and examining its isomorphism to Z4. Finally, it calculates the number of functions and bijections between sets and explores the number of elements in Sn satisfying specific conditions. Desklib offers a wealth of similar solved assignments and past papers to aid students in their studies.

DISCRETE MATHEMATICS
Assignment
[Pick the date]
Student Name

Question 1
(a) Smallest equivalence relation on the set { a , b , c , d , e } that contains the relation
{ ( a ,b ) , ( a ,c ) , ( d , c ) }
It can be said that an equivalence relation contains (a, b) then due to presence of symmetric it
will also contains (b, a).
Similarly,
R contains (a, a) (Transitive)
R contains (a, c) and also contains (c, a) (Symmetric)
R contains (c, a) and (a, b) contains (c, b) (Transitive)
R contains (b, c) (Symmetric)
R contains (d, e) and also contains (e, d) (Symmetric)
R contains (d, e) and also contains (e, d) (Transitive)
R contains (b, b) and (e, e), (c, c), (d, d) and (e, e)
Hence,
R= { ( a , a ) , ( b , b ) , ( c ,c ) , ( d , d ) , ( e ,e ) , ( a , b ) , ( b , a ) , ( a , c ) , ( c , a ) , ( c , b ) ( b , c ) , ( e , d ) , ( d , e ) }
(b) Equivalence classes of the equivalence relation
Equivalence classes are [a] and [d]
[ a ]= { a , b , c } = [ b ]=[c ]
[ d ] = {d , e }= [ d ] =[e]
1

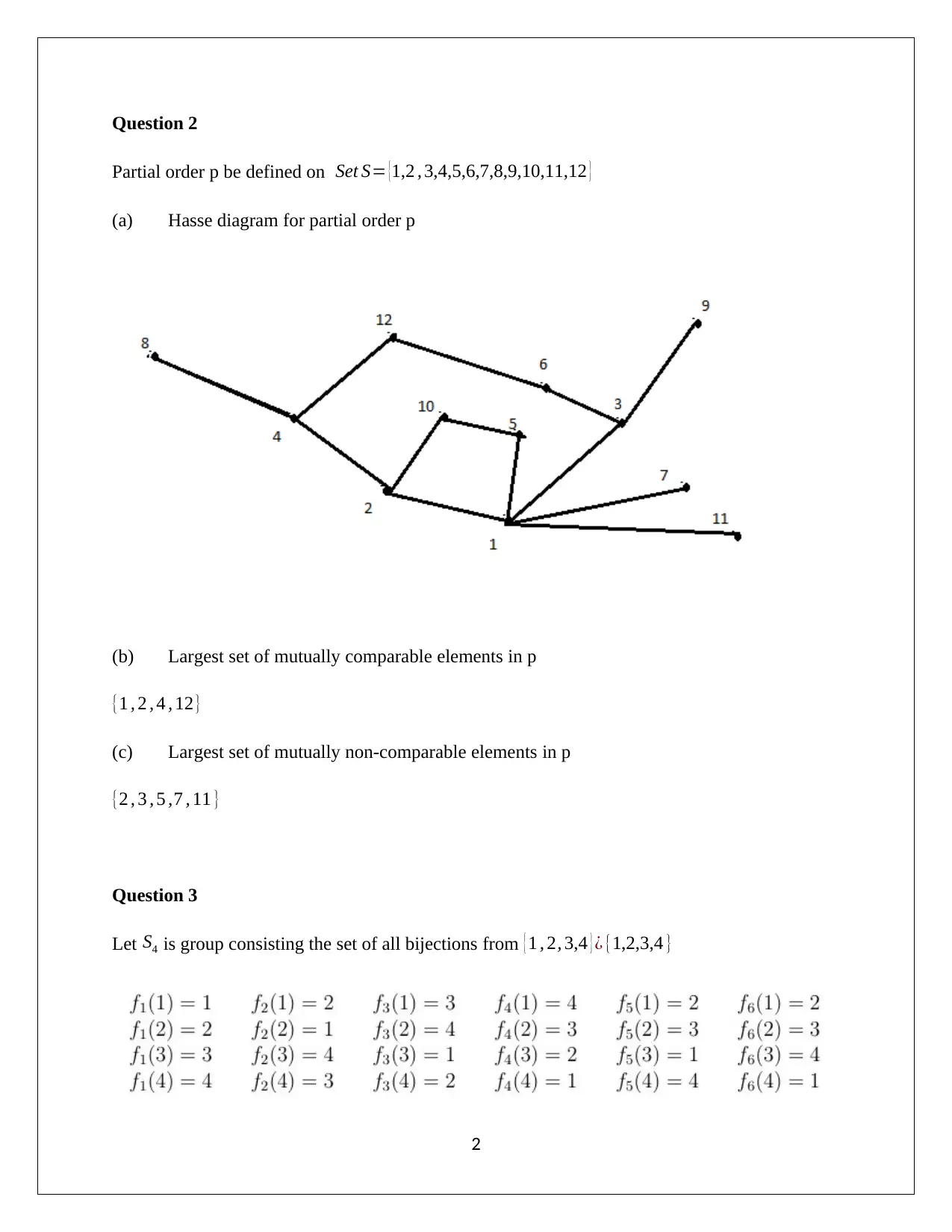
Question 2
Partial order p be defined on Set S= {1,2 , 3,4,5,6,7,8,9,10,11,12 }
(a) Hasse diagram for partial order p
(b) Largest set of mutually comparable elements in p
{1 , 2 , 4 , 12}
(c) Largest set of mutually non-comparable elements in p
{2 , 3 , 5 ,7 , 11 }
Question 3
Let S4 is group consisting the set of all bijections from { 1 , 2, 3,4 } ¿ {1,2,3,4 }
2

(a) Need to prove that {f 1 , f 2 , f 3 , f 4 }is subgroup of S4
Cayley Table needs to be made in order to prove the above statement.
f 1=(1 2 3
1 2 3
4
4 )
f 2=( 1 2 3
2 1 4
4
3 )
f 3=(1 2 3
3 4 1
4
2 )
f 4= ( 1 2 3
4 3 2
4
1 )
f 5=(1 2 3
2 3 1
4
5 )
f 6= ( 1 2 3
2 3 4
4
1 )
Here,
f 1 . f 1=f 1
f 1 . f 2=f 2
f 1 . f 3=f 3
f 1 . f 4=f 4
f 2 . f 1=f 2
f 3 . f 1=f 3
f 4 . f 1=f 4
Now,
3

f 2 . f 2=( 1 2 3
2 1 4
4
3 ) . ( 1 2 3
2 1 4
4
3 )= ( 1 2 3
1 2 3
4
4 )=f 1
f 2 . f 3=(1 2 3
2 1 4
4
3 ). (1 2 3
3 4 1
4
2 )=(1 2 3
4 3 2
4
1 )=f 4
f 2 . f 4= ( 1 2 3
2 1 4
4
3 ) . ( 1 2 3
4 3 2
4
1 )= ( 1 2 3
3 4 1
4
2 ) =f 3
f 3 . f 2=(1 2 3
3 4 1
4
2 ). (1 2 3
2 1 4
4
3 )=(1 2 3
4 3 2
4
1 )=f 4
f 3 . f 3=( 1 2 3
3 4 1
4
2 ) . ( 1 2 3
3 4 1
4
2 )=( 1 2 3
1 2 3
4
4 )=f 1
f 4 . f 2= (1 2 3
4 3 2
4
1 ). (1 2 3
2 1 4
4
3 )= (1 2 3
3 4 1
4
2 )=f 3
f 3 . f 4= ( 1 2 3
3 4 1
4
2 ) . ( 1 2 3
4 3 2
4
1 ) =( 1 2 3
2 1 4
4
3 ) =f 2
f 4 . f 3= (1 2 3
4 3 2
4
1 ). (1 2 3
3 4 1
4
2 )=(1 2 3
2 1 4
4
3 )=f 2
f 4 . f 4 =( 1 2 3
4 3 2
4
1 ) . ( 1 2 3
4 3 2
4
1 )=( 1 2 3
1 2 3
4
4 )=f 1
Therefore,
Cayley Table
0 f 1 f 2 f 3 f 4
f 1 f 1 f 2 f 3 f 4
f 1 f 2 f 3 f 4 f 3
f 3 f 3 f 4 f 1 f 2
f 4 f 4 f 3 f 2 f 1
Therefore, it can be seen from the Cayley table that that {f 1 , f 2 , f 3 , f 4 }is subgroup of S4 .
4

(b) Needs to find whether or not subgroup {f 1 , f 2 , f 3 , f 4 } in S4 isomorphic to ¿ ¿
It can be seen from Cayley table of subgroup {f 1 , f 2 , f 3 , f 4 }, each of the element is self-inverse.
However, in ¿ ¿inverse of 1 is 3 and inverse of 3 is 1. Hence, it is not possible to map all the
elements of { f 1 , f 2 , f 3 , f 4 }¿ {0 , 1 ,2,3 } .
Hence, it can be said that subgroup {f 1 , f 2 , f 3 , f 4 } in not isomorphic to ¿ ¿
(c) Cyclic subgroup ¿ f 5> ¿< f 6 >¿ in S4
For ¿ f 5> ¿
f 5=(1 2 3
2 3 1
4
5 )
f 5
2=f 5 . f 5=( 1 2 3
3 1 2
4
4 )
f 5
3=(1 2 3
1 2 3
4
4 )=f 1
¿ f 5>¿ { f 1 , f 5 , f 5
2 }
For ¿ f 6 >¿
f 6= (1 2 3
2 3 4
4
1 )
f 6
2=( 1 2 3
3 4 1
4
2 )
f 6
3=( 1 2 3
4 1 2
4
3 )
5

f 6
4= ( 1 2 3
1 2 3
4
4 ) =f 1
¿ f 6 >¿ { f 1 , f 6 , f 3 , f 6
3 }
Question 4
The requisite information and key points are summarized below:
 Let n is a positive integer
 Let Snis the group consisting the set of bijections from { 1,2 , … … .n } ¿ {1 , 2 , … … ….. n }
 Let Fn is the set of all functions from { 1,2 , … … .n } ¿ {1 , 2 , … … ….. n }
(a) |Fn|=?
It can be said that for each element of { 1,2 , … … .n }, there would be n number of images choice
and also, the total number of elements are and therefore,
Element 1 would have n number of possibilities
Element 2 would have n number of possibilities
.
.
.
.
Element n would have n number of possibilities
Hence,
{ 1 , 2, 3 , … … … . … … .n }
{n ,n , n , … … … … .. … .n }
6

Total number of possibilities would be ¿ nn
Thus, the conclusion can be made that |Fn|=nn
(b) Let the random function is selected as F5 .
The probability that it would be a bijection =?
|Fn|=|F5|
It means n = 5
|Fn|=|F5|=55
The bijection in this case would be from { 1 , 2, 3,4,5 } ¿ { 1, 2 , 3,4,5 }
Further,
{ 1 , 2, 3 , 4 ,5 }
{ 5 , 4 ,3 , 2 ,1 } Possibilities
It indicates that element would have 5 possibilities, element 2 would have 3 possibilities,
similarly, element 3, 4, and 5 would have 3,2 and 1 possibilities respectively.
Therefore,
Total number of bijections would be ¿ 5∗4∗3∗2∗1=5 !
Hence,
Total number of functions |F5|=55
Therefore, the probability that the selection function would be a bijection function would be
calculated below:
¿ 5!
55 = 120
3125 = 24
625
7

There is a 0.0384 probability that the selection function would be a bijection function.
(c) For n ≥ 2, number of element f of Sn for which f ( 1 ) ≠ 1∧f ( 2 ) ≠ 2
Here,
Sn=n!
Number of element f of Sn for which f ( 1 ) =1would be ( n−1 ) !
Number of element f of Sn for which f ( 2 ) =2would be ( n−1 ) !
Similarly,
Number of elements f for f(1) =1 or f(2) =2 would be 2(n-1)!
Hence, number of element f of Sn for which f ( 1 ) ≠ 1∧f ( 2 ) ≠ 2would be calculated below:
¿ n !−2 ( n−1 ) !
¿ ( n−1 ) !(n−2)
8

9