Discrete Mathematics

This document provides answers to various questions related to discrete mathematics. It covers topics such as functions, matrices, probability, graphs, and more. The document includes explanations, examples, and solutions to help students understand the concepts better.

Running head: Discrete Mathematics
DISCRETE MATHEMATICS
Name of the Student
Name of the university
Name of the author

1Mathematics
Part 1
Answer to the question 1:
a) As the domain of the mentioned relation is {a, b, c, d}.
Here c is an element of the domain set which has two possible range d and a, thus
relation is not a function of the set {a, b, c, d}.
b) As the domain of the mentioned relation is {a, b, c, d}.
Here, every element of the domain set has a defined range, thus this relation is a
function of the set {a, b, c, d}.
c) As the domain of the mentioned relation is {a, b, c, d}.
Here, every element of the domain set has a defined range, thus this relation is a
function of the set {a, b, c, d}.
d) As the domain of the mentioned relation is {a, b, c, d}.
Here, every element of the domain set has a defined range, thus this relation is a
function of the set {a, b, c, d}.
e) As the domain of the mentioned relation is {a, b, c, d}.
Here, every element of the domain set has a defined range, thus this relation is a
function of the set {a, b, c, d}.
Answer to the question 2:
a) The inverse of the function is f (A) is f-1(A) = {(e, a), (d, b), (b, c), (a, d), (d, e)}.
b) The inverse of the function is f (A) is f-1(A) = {(a, b), (d, c), (c, a), (a, d), (b, e)}.
c) The inverse of the function is f (A) is f-1(A) = {(a, a), (c, b), (b, c), (d, d), (e, e)}.
Answer to the question 3:
a) f(x) = 1/x
x = all the real numbers. Hence the answer will come in decimal form.

2Mathematics
f(x)= 1/2 = 0.5 where x= 2
Hence it is not a function.
b) f(x)= y such that y2 = x
For x = 2
y = √ 2
Hence, it is not a function for real number
c) f(x) = x2-1
Where x= 2
f(2)= 4 – 1
=3
Hence it is function for all real number.
Answer to the question 4:
a) The domain of the function is the set of all bit strings.
Domain= {0, 1, 00, 01, 10, 11, 000, 001, 0101, 011,….}
Co-domain= {0, 1, 00, 01, 10, 11, 000, 001, 0101, 011,….}
The range of this function is the set of all numbers of zeros in the bit string.
b) The function is f(x) = x2-3, domain of this function is (-∞ < x < ∞), interval notation
is (-∞, ∞). Range is f(x) ≥ -3, [-3, ∞]
Answer to the question 5:
a) One to one
f(x) = -3x+7
f(a) = f(b), a=b
-3a+7 = -3b+7

3Mathematics
a=b (hence it is one to one)
Onto
Let us assume,
f(x) = y belongs to all real numbers,
f(x) = y
-3x+7 = y
-3x = y-7
x = y-7/-3
Putting value of x in the equation, where x = y-7/-3
f(x) = -3(y-7/-3)+7
f(x) = y (proved)
The mentioned function is a bijective function since it satisfies the both one to one and onto.
b) One to one
f(x) = x2-2x+1
f(a) = f(b), if a = b
a2-2a+1 = b2-2b+1
a2-2a+2b-b2=0 (not proved)
hence this equation is not bijective.
c) One to one
f(x) = 3x3-3
f(a) = f(b) if a = b
3a3-3 = 3b3-3

4Mathematics
1
2
3
4
x
y
z
a3 = b3
a=b (Proved)
Onto
f(x) = 3x3-3,
f(x) = y belongs to all real numbers R
f(x) = y
3x3-3 = y
3x3 = y+3
x3 = y+3/3
x = 3
√ y +3/3
Now, putting the value of x in the function where, x = 3
√ y +3/3
f(x) = 3*(y+3/3)-3
f(x) = y (proved)
The mentioned function is a bijection function since it satisfies the both one to one and onto.
Answer to the question 6
a) R = {(1, x), (2, y), (3, z)}

5Mathematics
x
y
z
a
b
c
a
b
c
d
a
b
c
d
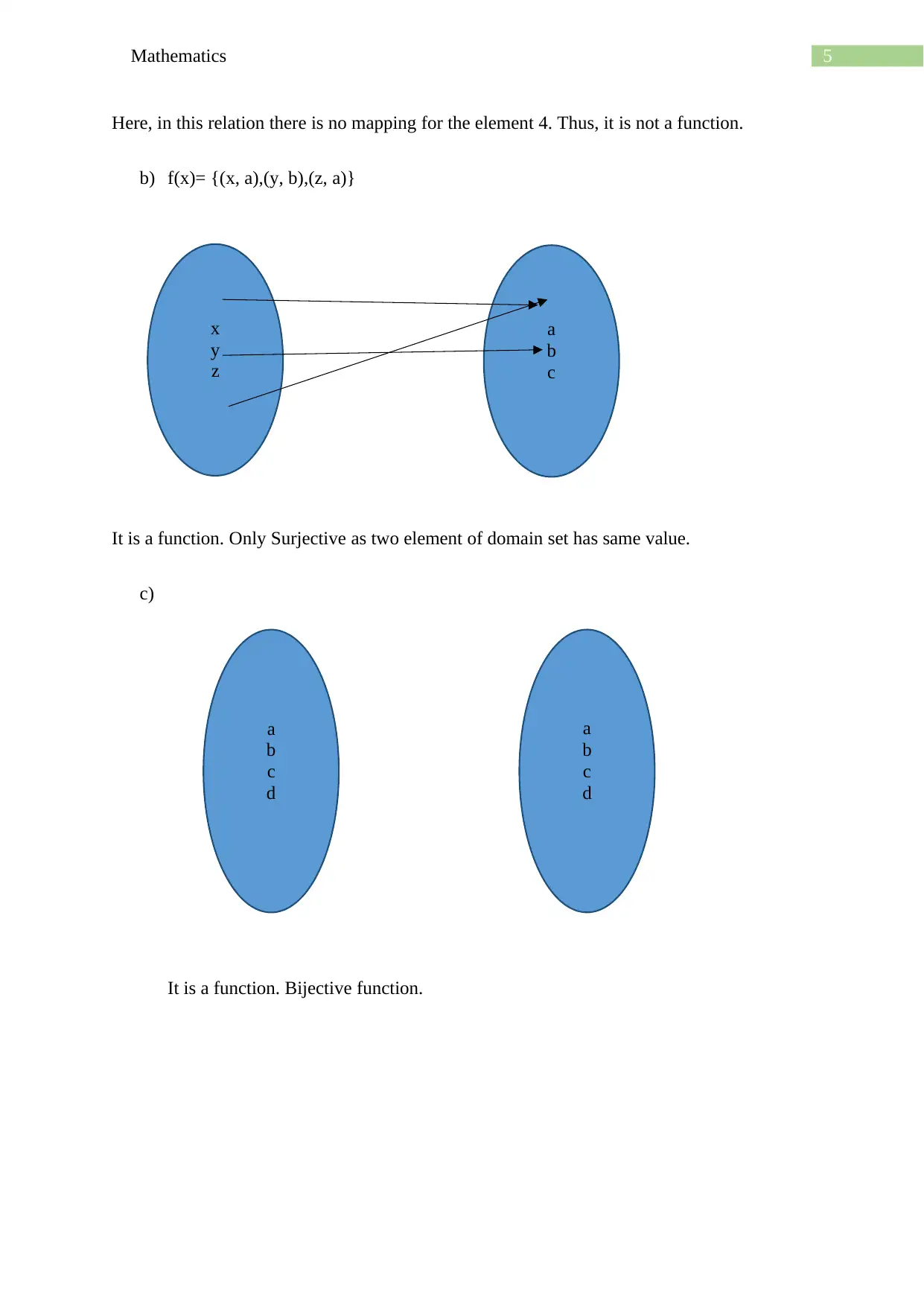
Here, in this relation there is no mapping for the element 4. Thus, it is not a function.
b) f(x)= {(x, a),(y, b),(z, a)}
It is a function. Only Surjective as two element of domain set has same value.
c)
It is a function. Bijective function.

6Mathematics
1
2
3
4
a
b
c
d
d)
It is a function. Surjective only.
Answer to the question 7
a) R = {(1,2), (2, 4),(3, 4),(4, 5)}
The above relation is a function as there every element of the domain set has an actual
value.
b) R = {(1,2), (2, 4),(2, 5),(4, 5)}
It is not a function as an element 2 present in domain set has two possible values.
Hence the actual value cannot be determined.
c) R = {(1,2), (2, 4),(4, 5)}
The above relation is a function as there every element of the domain set has an actual
value.
d) R= A × B
R is a function as the product of A and B will be real numbers which is present in the
set R.
Answer to the question 8
A= 6×4, B= 4×4, C= 5×4, D= 6×6

7Mathematics
a) AD is not defined as the numbers of columns are not equals to the number of rows.
b) AB is defined and the size of the matrix product is 6×4.
c) DA is defined and the size of the matrix product is 6×4.
d) BD is not defined as the number of columns are not equals to the number of rows.
Answer to the question 9
A= [3 2 −1
0 2 −2
5 −1 3 ] B= [ 2 5 3
−1 2 −5
2 −2 1 ]
A+B= [ 5 7 2
−1 4 −7
7 −3 4 ]
AB= [ 2 21 −2
−6 8 −12
17 17 23 ]
Answer to the question 10
P(A)= 0.15, P(B)= 0.31
a) P(Ā)= 0.85
b) P(AUB)= {0.15, 0.31}
c) P(A∩B)= empty set as there is nothing common between these two sets.
Answer to the question 11
a) Whole sample set: {(Black, Black), (black, white), (White, Black), (White, White)}.
b)

8Mathematics
17/20 3/20
16/19 2/19 16/19 2/19
Black White
Black White Black White
0
c) Total ball 20, black ball 17 and 3 white ball.
Probabilities of picking the second ball which colour is white 19C2 = 0.1342105263
d) Probabilities of picking the second ball with the colour is black 19C16 = 0.71578
Part B
Answer to question 1
a) Graph to represent the mentioned adjacency matrix:

9Mathematics
b) Graph to represent the mentioned adjacency matrix:
Answer to the question 2
a) Graph G has 6 vertices, and the degree sequence of the graph G is {5, 3, 2, 2, 2, 2}.
b) Graph G has 6 vertices, and the degree sequence of the graph G is {3, 3, 2, 2, 2, 2}.
c) Graph G has 6 vertices, and the degree sequence of the graph G is {3, 3, 3, 3, 2, 2}.
Answer to the question 3
a)
a b c d e f
a 0 1 1 0 0 0
b 1 0 1 0 0 0
c 1 1 0 1 1 1
d 0 0 1 0 1 0

10Mathematics
e 0 0 1 1 0 1
f 0 0 1 0 1 0
b)
a b c d e f
a 0 1 0 1 0 0
b 1 0 1 0 0 0
c 0 1 0 1 0 1
d 1 0 1 0 1 0
e 0 0 0 1 0 1
f 0 0 1 0 1 0
- a b c d e f
a 0 1 1 0 0 0
b 1 0 1 0 0 1
c 1 1 0 1 0 0
d 0 0 1 0 1 1
e 0 0 0 1 0 1
f 0 1 0 1 1 0

11Mathematics
c)
Answer to question 4
a)
E1 E2 E
3
E4 E
5
E6 E
7
E8
a 1 1 0 0 0 0 0 0
b 1 0 1 0 0 0 0 0
c 0 1 1 1 1 1 0 0
d 0 0 0 1 0 0 0 1
e 0 0 0 0 1 0 1 1
f 0 0 0 0 0 1 1 0

12Mathematics
b)
E1 E2 E3 E
4
E5 E6 E7
a 1 1 0 0 0 0 0
b 1 0 1 0 0 0 0
c 0 1 0 1 1 0 0
d 0 1 0 1 0 1 0
e 0 0 0 0 0 1 1
f 0 0 0 0 1 0 1
c)
E1 E2 E
3
E4 E5 E6 E
7
E8
a 1 1 0 0 0 0 0 0
b 1 0 1 1 0 0 0 0
c 0 1 1 0 1 0 0 0
d 0 0 0 0 1 1 1 0
e 0 0 0 0 0 1 0 1
f 0 0 0 0 0 0 1 1

13Mathematics
Answer to the question 5
In the above graph the Euler cycle does not exist. The graph will considered as Eulerian,
if it consist Euler Cycle. But, here in this graph there is no Euler cycle as the vertex c and e
has odd numbers of edges connected with it. In order to form an Euler Cycle all vertex must
contain even numbers of edges.
In the above graph the Euler cycle does not exist. The graph will considered as
Eulerian, if it consist Euler Cycle. But, here in this graph there is no Euler cycle as the vertex
c and d has odd numbers of edges connected with it. In order to form an Euler Cycle all
vertex must contain even numbers of edges.

14Mathematics
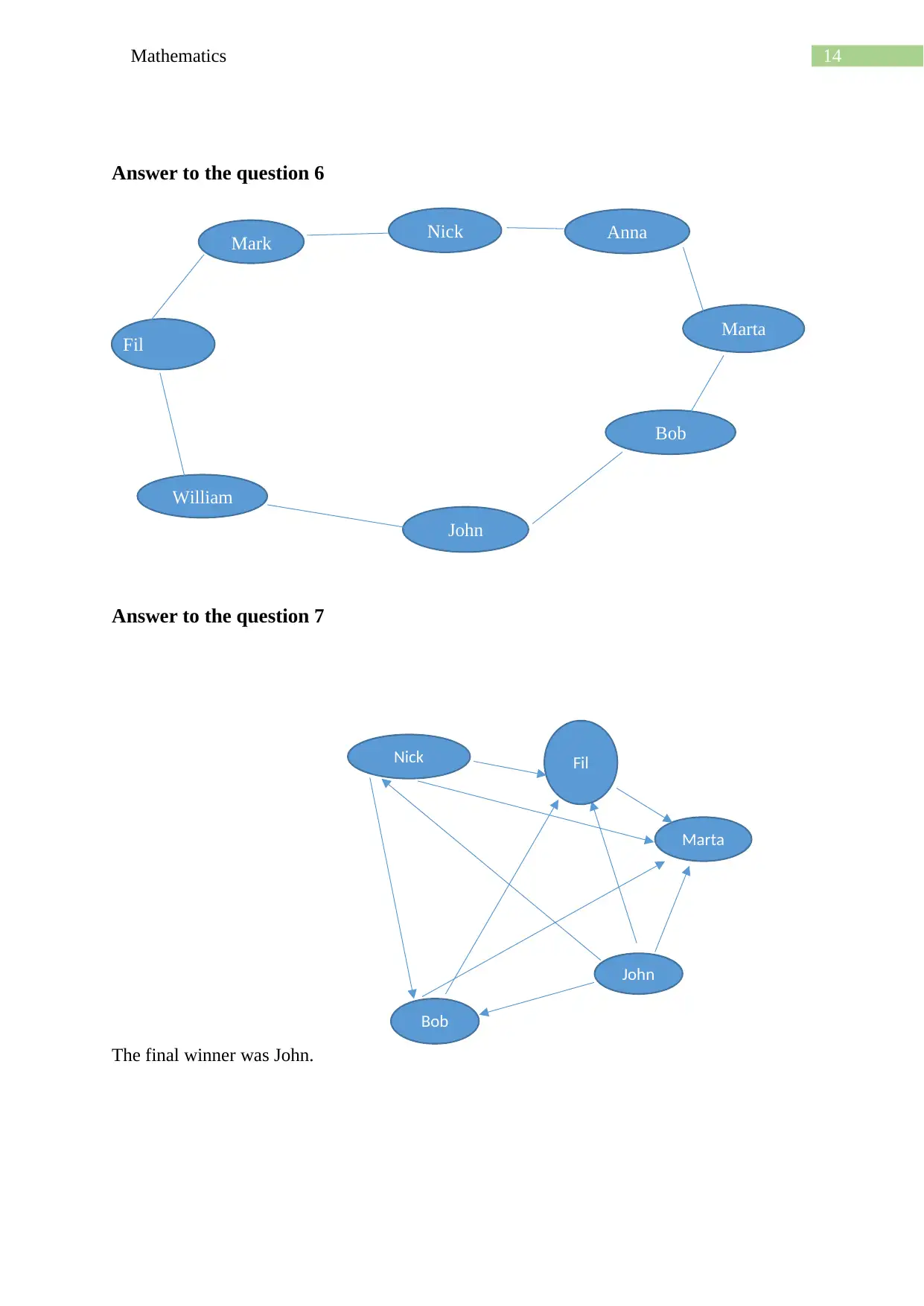
Answer to the question 6
Answer to the question 7
The final winner was John.
Nick Fil
Marta
Bob
John
Mark Nick Anna
Bob
John
William
Marta
Fil

15Mathematics
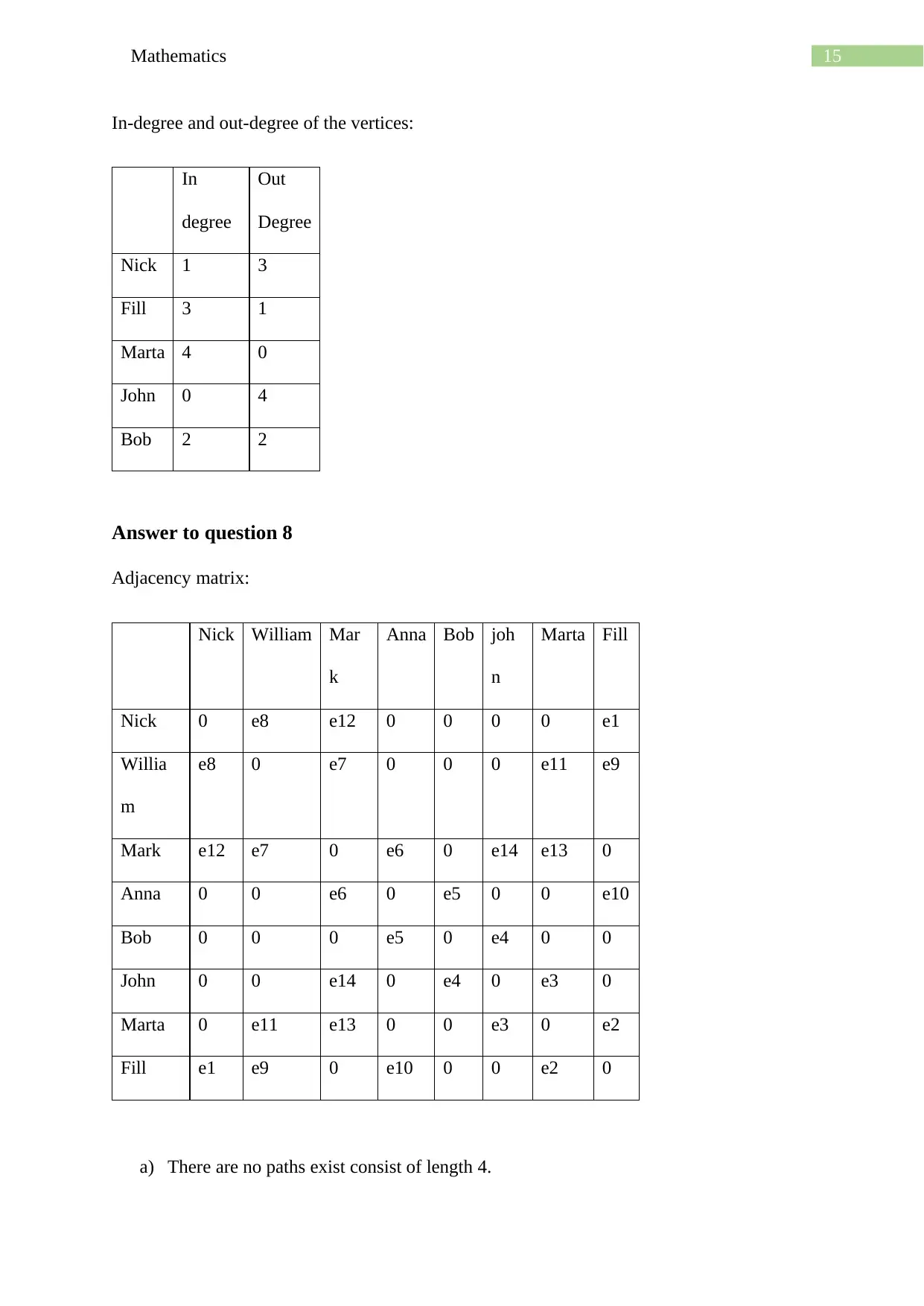
In-degree and out-degree of the vertices:
In
degree
Out
Degree
Nick 1 3
Fill 3 1
Marta 4 0
John 0 4
Bob 2 2
Answer to question 8
Adjacency matrix:
Nick William Mar
k
Anna Bob joh
n
Marta Fill
Nick 0 e8 e12 0 0 0 0 e1
Willia
m
e8 0 e7 0 0 0 e11 e9
Mark e12 e7 0 e6 0 e14 e13 0
Anna 0 0 e6 0 e5 0 0 e10
Bob 0 0 0 e5 0 e4 0 0
John 0 0 e14 0 e4 0 e3 0
Marta 0 e11 e13 0 0 e3 0 e2
Fill e1 e9 0 e10 0 0 e2 0
a) There are no paths exist consist of length 4.

16Mathematics
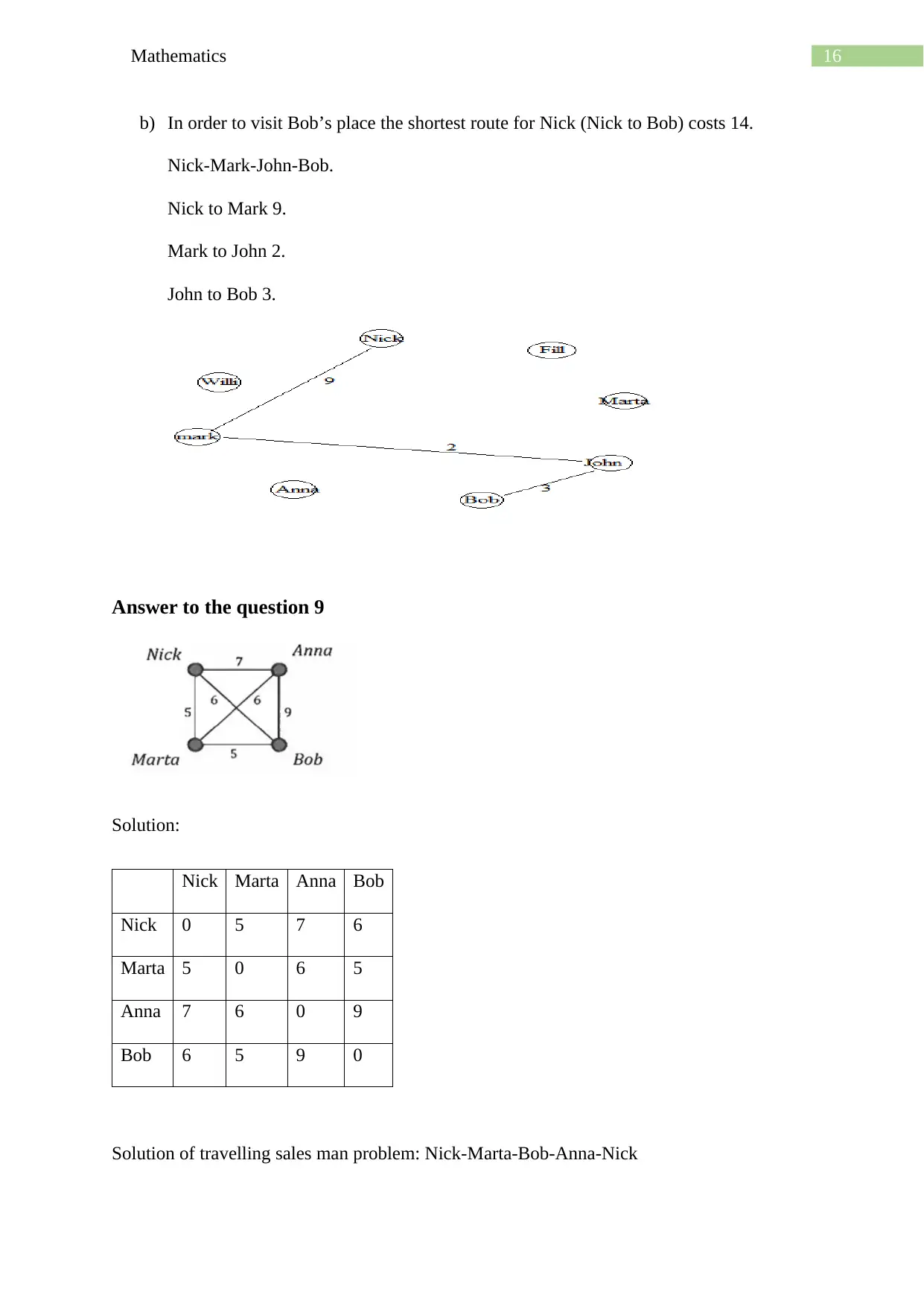
b) In order to visit Bob’s place the shortest route for Nick (Nick to Bob) costs 14.
Nick-Mark-John-Bob.
Nick to Mark 9.
Mark to John 2.
John to Bob 3.
Answer to the question 9
Solution:
Nick Marta Anna Bob
Nick 0 5 7 6
Marta 5 0 6 5
Anna 7 6 0 9
Bob 6 5 9 0
Solution of travelling sales man problem: Nick-Marta-Bob-Anna-Nick

17Mathematics
Total travelling cost: (5 + 5 + 9+7) = 26
Answer to question 10
Binary search tree for the sentence “It takes a great deal of bravery to stand up your enemies,
but a great deal more to stand up to your friends.
Answer to question 11
Huffman Compression of “HAPPY BIRTHDAY”

18Mathematics
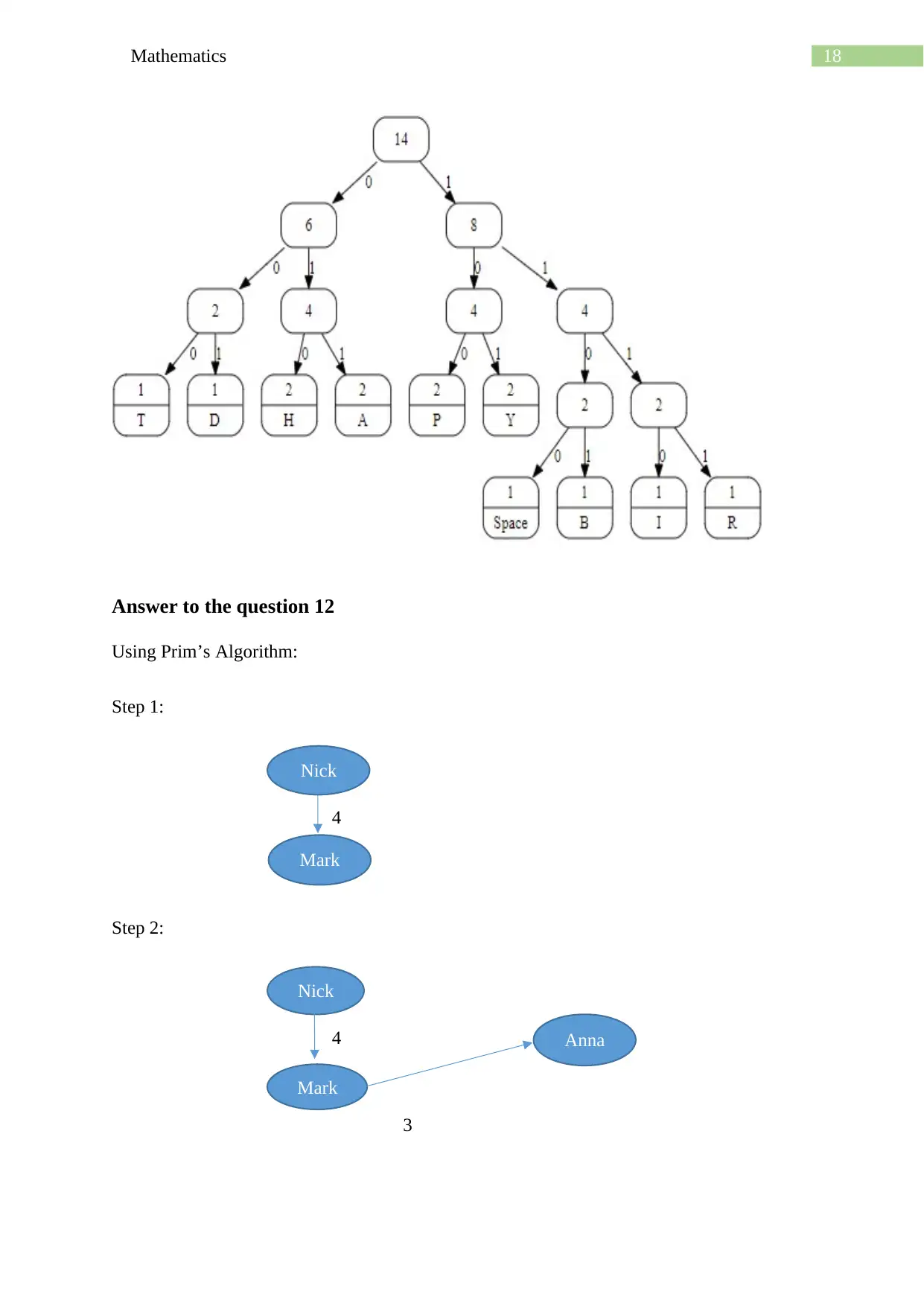
Answer to the question 12
Using Prim’s Algorithm:
Step 1:
4
Step 2:
5
4
Nick
Mark
Nick
Mark
Anna
3

19Mathematics
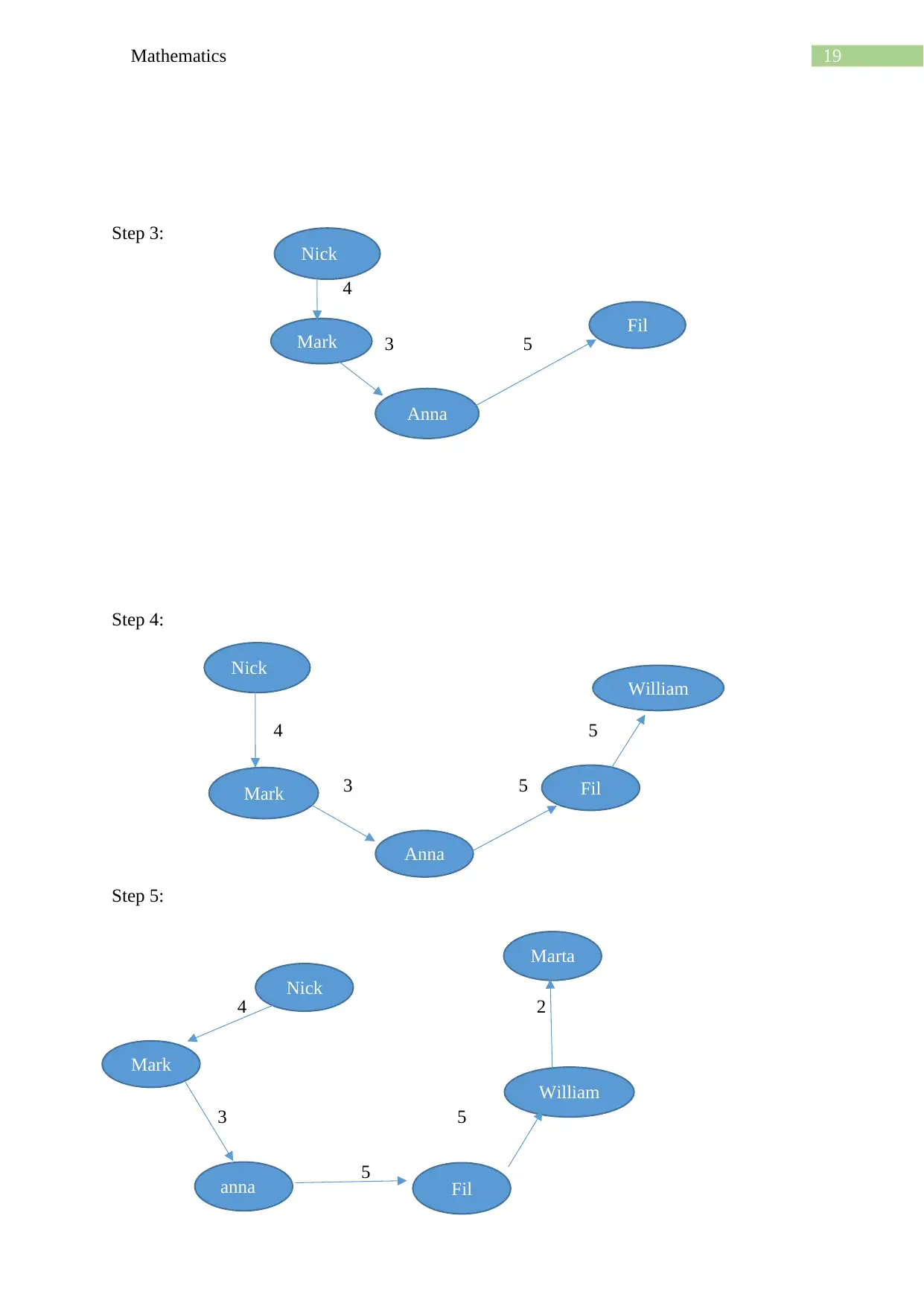
Step 3:
4
3 5
Step 4:
4 5
3 5
Step 5:
4 2
3 5
5
Anna
Nick
Mark Fil
Nick
Mark
Anna
Fil
William
Nick
Mark
anna Fil
William
Marta

20Mathematics
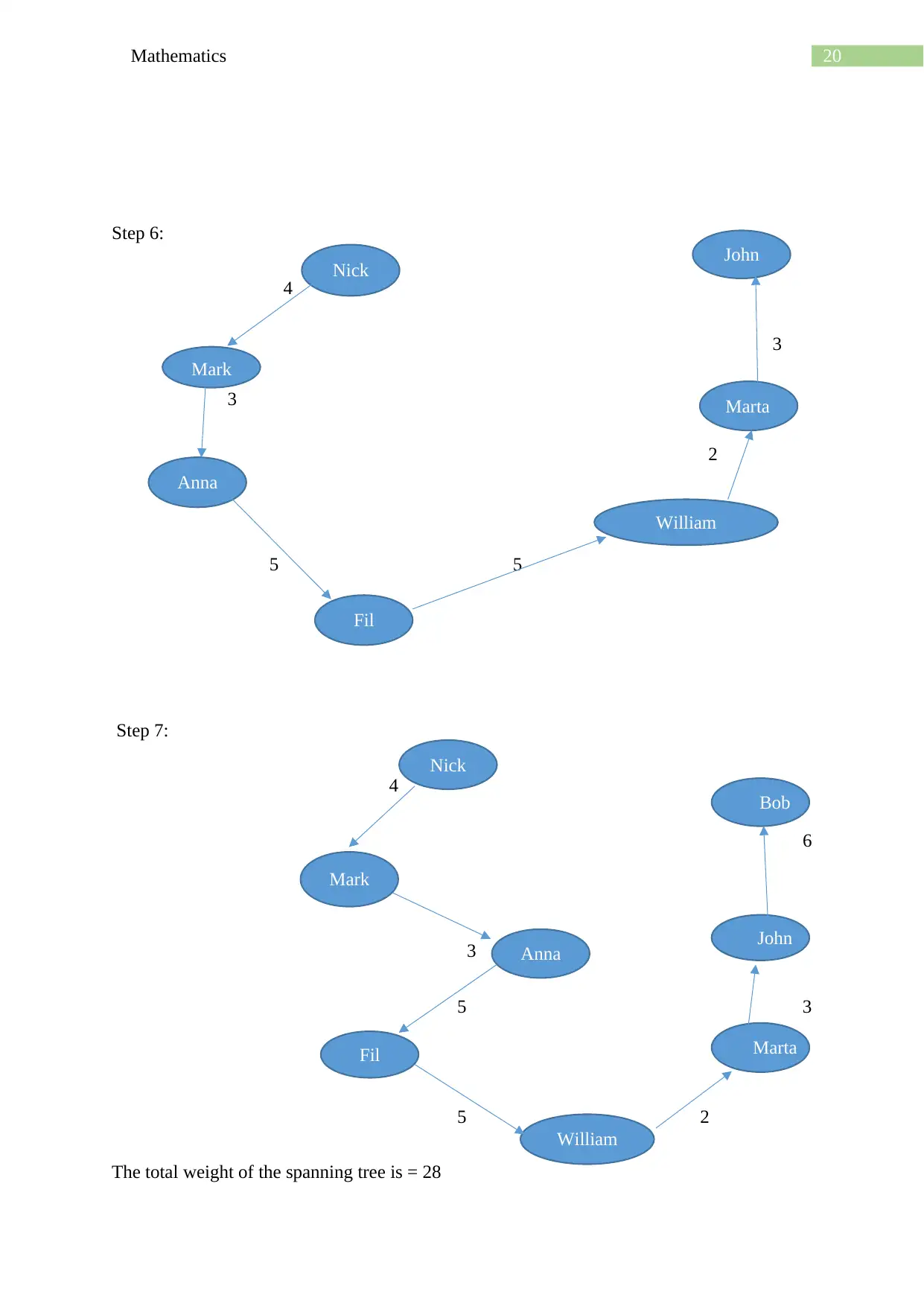
Step 6:
4
3
3
2
5 5
Step 7:
4
6
3
5 3
5 2
The total weight of the spanning tree is = 28
John
Nick
Mark
Anna
Fil
William
Marta
Nick
Mark
Anna
Fil
William
Marta
John
Bob

21Mathematics
Bibliography
Jech, T., 2013. Set theory. Springer Science & Business Media.
Zimmermann, H.J., 2011. Fuzzy set theory—and its applications. Springer Science &
Business Media.
Deo, N., 2017. Graph theory with applications to engineering and computer science. Courier
Dover Publications.
Heckmann, T., Schwanghart, W. and Phillips, J.D., 2015. Graph theory—Recent
developments of its application in geomorphology. Geomorphology, 243, pp.130-146.
Gupta, A.K. and Nagar, D.K., 2018. Matrix variate distributions. Chapman and Hall/CRC.
Graham, A., 2018. Kronecker products and matrix calculus with applications. Courier Dover
Publications.
Ferreira, S.S., Passos, C.P., Madureira, P., Vilanova, M. and Coimbra, M.A., 2015.
Structure–function relationships of immunostimulatory polysaccharides: A
review. Carbohydrate polymers, 132, pp.378-396.
Allendorf, M.D. and Stavila, V., 2015. Crystal engineering, structure–function relationships,
and the future of metal–organic frameworks. CrystEngComm, 17(2), pp.229-246.
Ramsey, F.P., 2016. Truth and probability. In Readings in Formal Epistemology (pp. 21-45).
Springer, Cham.

22Mathematics
Tang, D., Carlet, C. and Tang, X., 2015. Differentially 4-uniform bijections by permuting the
inverse function. Designs, Codes and Cryptography, 77(1), pp.117-141.