Discrete Mathematics Assignment Solutions
VerifiedAdded on 2022/11/18
|20
|2548
|339
AI Summary
The article provides solutions for Discrete Mathematics assignments covering topics like binary multiplication, compound statements, set theory, sorting algorithms, and more. It also includes a proof for a function and a determinant calculation. The content is suitable for students studying Discrete Mathematics in college or university.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Running head: DISCRETE MATHEMATICS
DISCRETE MATHEMATICS
Name of the Student
Name of the University
Author Note
DISCRETE MATHEMATICS
Name of the Student
Name of the University
Author Note
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

1DISCRETE MATHEMATICS
Question 1:
a) (175773)10 to ()5
This can be obtained by dividing the number by 5 and then taking out the remainders in
descending order.
Diviso
r
Dividend Remainder
5 175773 3
5 35154 4
5 7030 0
5 1406 1
5 281 1
5 11 1
5 2 2
0
(175773)10 = (21111043)5
b) (22.5602)10 can be converted to base 8 by dividing the number by 8 and then taking the
remainders.
Diviso
r
Dividend Remainder
8 22 6
2
Question 1:
a) (175773)10 to ()5
This can be obtained by dividing the number by 5 and then taking out the remainders in
descending order.
Diviso
r
Dividend Remainder
5 175773 3
5 35154 4
5 7030 0
5 1406 1
5 281 1
5 11 1
5 2 2
0
(175773)10 = (21111043)5
b) (22.5602)10 can be converted to base 8 by dividing the number by 8 and then taking the
remainders.
Diviso
r
Dividend Remainder
8 22 6
2

2DISCRETE MATHEMATICS
product remainder whole
number
0.5602*
8
4.4816 0.4816 4
0.4816*
8
3.8528 0.8528 3
0.8528*
8
6.8224 0.8224 6
0.8528*
8
6.5792 0.5792 6
0.5792*
8
4.6336 0.6336 4
(22.5602)10 = (26.43664)8
ii) (FBCF9)16 + (3AFD7)16
a)
In the hexadecimal addition if the sum is more than F then carry is added to the previous
addition bit.
FBCF9
3AFD7
= 136CD0
b) (5432)8 – (574)8 = (4636)8
product remainder whole
number
0.5602*
8
4.4816 0.4816 4
0.4816*
8
3.8528 0.8528 3
0.8528*
8
6.8224 0.8224 6
0.8528*
8
6.5792 0.5792 6
0.5792*
8
4.6336 0.6336 4
(22.5602)10 = (26.43664)8
ii) (FBCF9)16 + (3AFD7)16
a)
In the hexadecimal addition if the sum is more than F then carry is added to the previous
addition bit.
FBCF9
3AFD7
= 136CD0
b) (5432)8 – (574)8 = (4636)8

3DISCRETE MATHEMATICS
Octal subtraction is like the subtraction in any other number system. Only difference is in the
borrow part, in decimal number system a group of 1010 is borrowed and in octal number
system a group of 810 is borrowed.
c) (110010101)2 X (1100)2
Binary multiplication rules are
0X0 = 0, 1X0 = 0, 0X1 = 0 and 1X1 = 1.
This follows the same multiplication structure of decimal multiplication where each digit of
one number is multiplied with every digit of other number in corresponding one bit shifted
lines and finally all those lines are added.
Hence, (110010101)2 X (1100)2 = (1001011111100)2
Question 2:
i. A compound statement is a tautology if the statement is true irrespective of the truth of
individual statements. Compound statement is a contradiction if the statement is always false
irrespective of the values of individual statements. A compound statement is satisfiable if at
least one truth statement for one or more truth values of the individuals.
In the statement (~𝑎∨~𝑏) ˅ (𝑎∧𝑏) the individual statements are a, b, (~𝑎∨~𝑏) and (𝑎∧𝑏).
In the truth table 1 is considered truth and 0 is considered false.
a b (~𝑎∨~𝑏) (𝑎∧𝑏) (~𝑎∨~𝑏) ˅
(𝑎∧𝑏)
0 0 1 0 1
0 1 1 0 1
1 0 1 0 1
Octal subtraction is like the subtraction in any other number system. Only difference is in the
borrow part, in decimal number system a group of 1010 is borrowed and in octal number
system a group of 810 is borrowed.
c) (110010101)2 X (1100)2
Binary multiplication rules are
0X0 = 0, 1X0 = 0, 0X1 = 0 and 1X1 = 1.
This follows the same multiplication structure of decimal multiplication where each digit of
one number is multiplied with every digit of other number in corresponding one bit shifted
lines and finally all those lines are added.
Hence, (110010101)2 X (1100)2 = (1001011111100)2
Question 2:
i. A compound statement is a tautology if the statement is true irrespective of the truth of
individual statements. Compound statement is a contradiction if the statement is always false
irrespective of the values of individual statements. A compound statement is satisfiable if at
least one truth statement for one or more truth values of the individuals.
In the statement (~𝑎∨~𝑏) ˅ (𝑎∧𝑏) the individual statements are a, b, (~𝑎∨~𝑏) and (𝑎∧𝑏).
In the truth table 1 is considered truth and 0 is considered false.
a b (~𝑎∨~𝑏) (𝑎∧𝑏) (~𝑎∨~𝑏) ˅
(𝑎∧𝑏)
0 0 1 0 1
0 1 1 0 1
1 0 1 0 1
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

4DISCRETE MATHEMATICS
1 1 0 1 1
Hence, the compound statement is always truth irrespective of the truth of individual
statement and hence the compound statement is a tautology.
ii. (𝑝∨~𝑞)∧(𝑝∧𝑞)≡(𝑝∧𝑞)
Truth table:
p q (𝑝∨~𝑞) (𝑝∧𝑞) (𝑝∨~𝑞)∧(𝑝∧
𝑞)
0 0 1 0 0
0 1 0 0 0
1 0 1 0 0
1 1 1 1 1
Hence, as the two truth tables of (𝑝∧𝑞) and (𝑝∨~𝑞)∧(𝑝∧𝑞) are same so, both expressions
are equivalent.
iii. truth table of statements are given below.
p q r s 𝐩→(𝐪 ^
𝐫)
𝐫→𝐬 𝐬→𝐪 ~𝐩 ∴𝐬
F F F F T T T F
F F F T T T F T
F F T F T F T F
F F T T T T T T
1 1 0 1 1
Hence, the compound statement is always truth irrespective of the truth of individual
statement and hence the compound statement is a tautology.
ii. (𝑝∨~𝑞)∧(𝑝∧𝑞)≡(𝑝∧𝑞)
Truth table:
p q (𝑝∨~𝑞) (𝑝∧𝑞) (𝑝∨~𝑞)∧(𝑝∧
𝑞)
0 0 1 0 0
0 1 0 0 0
1 0 1 0 0
1 1 1 1 1
Hence, as the two truth tables of (𝑝∧𝑞) and (𝑝∨~𝑞)∧(𝑝∧𝑞) are same so, both expressions
are equivalent.
iii. truth table of statements are given below.
p q r s 𝐩→(𝐪 ^
𝐫)
𝐫→𝐬 𝐬→𝐪 ~𝐩 ∴𝐬
F F F F T T T F
F F F T T T F T
F F T F T F T F
F F T T T T T T

5DISCRETE MATHEMATICS
As in the first row all the premises are true and the conclusion is false hence the argument is
invalid.
iv. Let,
x1 : The weather is not nice today
x2 : its cold outside
x3 : we will go fishing
x4: Then we will go to the Snowy mountains
x5: We will ski there
Question 3:
i.
Total number of subjects = 50.
41 reported relief from at least one of the drugs.
Hence, the number of people relived from none of the drugs = 50 – 41 = 9.
b. number of people relived from three drugs = relived from at least one drug – (relived from
drug A and B + relived from drug A and C + relived from drug B and C) = 41 – (9+14+15) =
41 – 38 = 3 subjects.
c.
Venn diagram:
BA
C
A and B
and C = 3
A and B
= 9
B and C=
15
As in the first row all the premises are true and the conclusion is false hence the argument is
invalid.
iv. Let,
x1 : The weather is not nice today
x2 : its cold outside
x3 : we will go fishing
x4: Then we will go to the Snowy mountains
x5: We will ski there
Question 3:
i.
Total number of subjects = 50.
41 reported relief from at least one of the drugs.
Hence, the number of people relived from none of the drugs = 50 – 41 = 9.
b. number of people relived from three drugs = relived from at least one drug – (relived from
drug A and B + relived from drug A and C + relived from drug B and C) = 41 – (9+14+15) =
41 – 38 = 3 subjects.
c.
Venn diagram:
BA
C
A and B
and C = 3
A and B
= 9
B and C=
15

6DISCRETE MATHEMATICS
d. Number of subjects that only got relief from A = 14 + 9- 21 = 2 subjects.
ii. (Q-P) ∩(R-P) = (𝑸 ∩𝑹)−𝑷
Venn diagram:
Q
Hence, from the above Venn diagram it can be seen that the two areas are the same. Hence,
the two set identities are equal.
Question 4:
The list in the entry order from left to right is the following.
9,3,7,5,2,1.
i. Insertion sort:
Steps comparisons
0 9 3 7 5 2 1 0
1 3 9 7 5 2 1 1
2 3 7 9 5 2 1 2
A and C=
9
P
R
(𝑸 ∩𝑹)−𝑷
(Q-P) ∩(R-P)
d. Number of subjects that only got relief from A = 14 + 9- 21 = 2 subjects.
ii. (Q-P) ∩(R-P) = (𝑸 ∩𝑹)−𝑷
Venn diagram:
Q
Hence, from the above Venn diagram it can be seen that the two areas are the same. Hence,
the two set identities are equal.
Question 4:
The list in the entry order from left to right is the following.
9,3,7,5,2,1.
i. Insertion sort:
Steps comparisons
0 9 3 7 5 2 1 0
1 3 9 7 5 2 1 1
2 3 7 9 5 2 1 2
A and C=
9
P
R
(𝑸 ∩𝑹)−𝑷
(Q-P) ∩(R-P)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
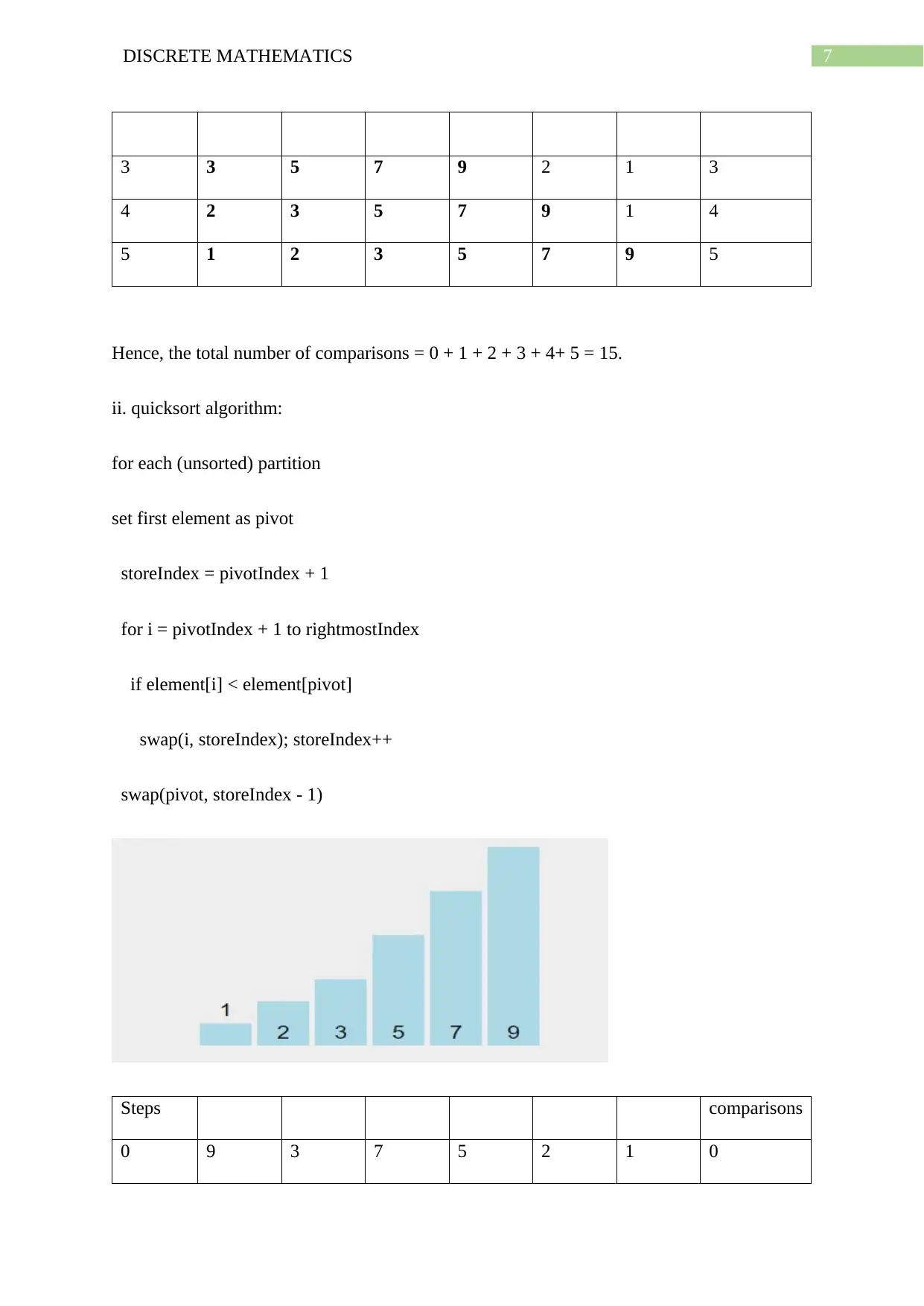
7DISCRETE MATHEMATICS
3 3 5 7 9 2 1 3
4 2 3 5 7 9 1 4
5 1 2 3 5 7 9 5
Hence, the total number of comparisons = 0 + 1 + 2 + 3 + 4+ 5 = 15.
ii. quicksort algorithm:
for each (unsorted) partition
set first element as pivot
storeIndex = pivotIndex + 1
for i = pivotIndex + 1 to rightmostIndex
if element[i] < element[pivot]
swap(i, storeIndex); storeIndex++
swap(pivot, storeIndex - 1)
Steps comparisons
0 9 3 7 5 2 1 0
3 3 5 7 9 2 1 3
4 2 3 5 7 9 1 4
5 1 2 3 5 7 9 5
Hence, the total number of comparisons = 0 + 1 + 2 + 3 + 4+ 5 = 15.
ii. quicksort algorithm:
for each (unsorted) partition
set first element as pivot
storeIndex = pivotIndex + 1
for i = pivotIndex + 1 to rightmostIndex
if element[i] < element[pivot]
swap(i, storeIndex); storeIndex++
swap(pivot, storeIndex - 1)
Steps comparisons
0 9 3 7 5 2 1 0

8DISCRETE MATHEMATICS
1 3 7 5 2 1 9 5
2 2 1 3 7 5 9 4
3 1 2 3 5 7 9 4
Hence, total number of comparisons = 5+4+4 = 13.
iii. Bubble sort
do
swapped = false
for i = 1 to indexOfLastUnsortedElement-1
if leftElement > rightElement
swap(leftElement, rightElement)
swapped = true
while swapped
Pass comparisons
0 9 3 7 5 2 1 0
1 3 7 5 2 1 9 5
2 3 5 2 1 7 9 5
3 3 2 1 5 7 9 5
4 2 1 3 5 7 9 5
5 1 2 3 5 7 9 5
Total number of comparisons = 5 + 5 + 5 + 5 +5 =25.
The sorted sequence is 1,2,3,5,7,9.
1 3 7 5 2 1 9 5
2 2 1 3 7 5 9 4
3 1 2 3 5 7 9 4
Hence, total number of comparisons = 5+4+4 = 13.
iii. Bubble sort
do
swapped = false
for i = 1 to indexOfLastUnsortedElement-1
if leftElement > rightElement
swap(leftElement, rightElement)
swapped = true
while swapped
Pass comparisons
0 9 3 7 5 2 1 0
1 3 7 5 2 1 9 5
2 3 5 2 1 7 9 5
3 3 2 1 5 7 9 5
4 2 1 3 5 7 9 5
5 1 2 3 5 7 9 5
Total number of comparisons = 5 + 5 + 5 + 5 +5 =25.
The sorted sequence is 1,2,3,5,7,9.

9DISCRETE MATHEMATICS
iv. Selection sort:
repeat (numOfElements - 1) times
set the first unsorted element as the minimum
for each of the unsorted elements
if element < currentMinimum
set element as new minimum
swap minimum with first unsorted position
Steps comparisons
0 9 3 7 5 2 1 0
1 1 3 7 5 2 9 5
2 1 2 7 5 3 9 4
3 1 2 3 5 7 9 3
Total number of comparisons = 5 + 4 + 3 = 12.
The sorted sequence is 1,2,3,5,7,9.
v. Merge sort:
split each element into partitions of size 1
recursively merge adjacent partitions
for i = leftPartIdx to rightPartIdx
if leftPartHeadValue <= rightPartHeadValue
copy leftPartHeadValue
iv. Selection sort:
repeat (numOfElements - 1) times
set the first unsorted element as the minimum
for each of the unsorted elements
if element < currentMinimum
set element as new minimum
swap minimum with first unsorted position
Steps comparisons
0 9 3 7 5 2 1 0
1 1 3 7 5 2 9 5
2 1 2 7 5 3 9 4
3 1 2 3 5 7 9 3
Total number of comparisons = 5 + 4 + 3 = 12.
The sorted sequence is 1,2,3,5,7,9.
v. Merge sort:
split each element into partitions of size 1
recursively merge adjacent partitions
for i = leftPartIdx to rightPartIdx
if leftPartHeadValue <= rightPartHeadValue
copy leftPartHeadValue
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

10DISCRETE MATHEMATICS
else: copy rightPartHeadValue
copy elements back to original array
Merge
sort
Comparison
s Step Parts
0 0
9,3,7,5,2,
1
0 1 9,3,7 5,2,1
0 2 9,3 7 5,2 1
0 3 9 3 7 5 2 1
3 4 3,9 5,7 1,2
3 5 3,5,7,9 1,2
8 6
1,2,3,5,7,
9
Hence, total number of comparisons = 3+3+8 = 14.
In increasing order after merge sorting the sequence will be 1,2,3,5,7,9.
The sorted sequence is 1,2,3,5,7,9.
Question 5:
A = {1, 2, 3, 4, 5,6,7}
Ordered pairs of R = {(1,1),(2,2),(2,5),(3,2),(3,3),(3,4),(3,5),(3,6),(4,4),(4,5),(6,6),(7,1),(7,7)}
else: copy rightPartHeadValue
copy elements back to original array
Merge
sort
Comparison
s Step Parts
0 0
9,3,7,5,2,
1
0 1 9,3,7 5,2,1
0 2 9,3 7 5,2 1
0 3 9 3 7 5 2 1
3 4 3,9 5,7 1,2
3 5 3,5,7,9 1,2
8 6
1,2,3,5,7,
9
Hence, total number of comparisons = 3+3+8 = 14.
In increasing order after merge sorting the sequence will be 1,2,3,5,7,9.
The sorted sequence is 1,2,3,5,7,9.
Question 5:
A = {1, 2, 3, 4, 5,6,7}
Ordered pairs of R = {(1,1),(2,2),(2,5),(3,2),(3,3),(3,4),(3,5),(3,6),(4,4),(4,5),(6,6),(7,1),(7,7)}

11DISCRETE MATHEMATICS
The range of relation R as evident from graph is 1 to 7.
The domain of relation R is 1 to 7.
The relation is reflexive as every point in A is a point in R.
The relation is anti-symmetric as when (x,y) and (y,x) belongs to R then x = y.
The relation R is not transitive as for every (x,y) and (y,x) belongs to R not always x=y. As
an example (3,4) and (4,5) are in R but 3 ≠5.
Hence, as one condition is not satisfied, although two conditions are satisfied, hence R is not
a partial order.
As for every x there are more y values, hence the relation R is not a function.
Question 6:
i.
Required to be proved
f ( a ) =3 a3 – 2a – 6 is O ( a3 )
= ||3a^3|| + ||2a^3|| + ||6a^3||
= 11 a3
Hence, by taking c = 11 and m=1
|3 a3 – 2a – 6|≤11 a3
|3 – 2 – 6| <= 11 a3 – 5≤11a3
Hence, f(a) is O ( a3 )
ii. Required to be proved
The range of relation R as evident from graph is 1 to 7.
The domain of relation R is 1 to 7.
The relation is reflexive as every point in A is a point in R.
The relation is anti-symmetric as when (x,y) and (y,x) belongs to R then x = y.
The relation R is not transitive as for every (x,y) and (y,x) belongs to R not always x=y. As
an example (3,4) and (4,5) are in R but 3 ≠5.
Hence, as one condition is not satisfied, although two conditions are satisfied, hence R is not
a partial order.
As for every x there are more y values, hence the relation R is not a function.
Question 6:
i.
Required to be proved
f ( a ) =3 a3 – 2a – 6 is O ( a3 )
= ||3a^3|| + ||2a^3|| + ||6a^3||
= 11 a3
Hence, by taking c = 11 and m=1
|3 a3 – 2a – 6|≤11 a3
|3 – 2 – 6| <= 11 a3 – 5≤11a3
Hence, f(a) is O ( a3 )
ii. Required to be proved

12DISCRETE MATHEMATICS
f(x) = (3x-2)(2x-9) is O ( x2 )
(3x-2)(2x-9) = 6 x2 – 27 x – 4 x +18 = 6 x2 – 31 x +18 = |6 x2
|+|31 x2
|+|18 x2
|
= 55 x2
Hence, by considering c = 55, m = 1
|6-23+18| <= 55x^2
11 ≤55 x2
Hence, f ( x )=O ( x2 )
Question 7:
B = [−1 4 0
2 −3 2
1 0 2 ]
B−1 = Adj ( A )
Det ( A )
Co-factor= ( −1 ) row num+ column num*Bminor
Bminor(1,1) = [ −3 2
0 2 ], Bminor(1,2) = [ 2 2
1 2 ], Bminor(1,3) = [ 2 −3
1 0 ]
Bminor(2,1) = [4 0
0 2 ], Bminor(2,2) = [−1 0
1 2 ], Bminor(2,3) = [−1 4
1 0 ]
Bminor(3,1) = [ 4 0
−3 2 ], Bminor(3,2) = [ −1 0
2 2 ], Bminor(3,3) = [ −1 4
2 −3 ]
f(x) = (3x-2)(2x-9) is O ( x2 )
(3x-2)(2x-9) = 6 x2 – 27 x – 4 x +18 = 6 x2 – 31 x +18 = |6 x2
|+|31 x2
|+|18 x2
|
= 55 x2
Hence, by considering c = 55, m = 1
|6-23+18| <= 55x^2
11 ≤55 x2
Hence, f ( x )=O ( x2 )
Question 7:
B = [−1 4 0
2 −3 2
1 0 2 ]
B−1 = Adj ( A )
Det ( A )
Co-factor= ( −1 ) row num+ column num*Bminor
Bminor(1,1) = [ −3 2
0 2 ], Bminor(1,2) = [ 2 2
1 2 ], Bminor(1,3) = [ 2 −3
1 0 ]
Bminor(2,1) = [4 0
0 2 ], Bminor(2,2) = [−1 0
1 2 ], Bminor(2,3) = [−1 4
1 0 ]
Bminor(3,1) = [ 4 0
−3 2 ], Bminor(3,2) = [ −1 0
2 2 ], Bminor(3,3) = [ −1 4
2 −3 ]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
13DISCRETE MATHEMATICS
Det(A) = -1*Cofact(1,1) – 4*Cofact(1,2) + 0*Cofact(1,3) = -1(-6-0) -4*(4-2) = 6 -8 = -2
Adj(A) = [cofact ( 1,1 ) cofact ( 1,2 ) cofact (1,3 )
cofact ( 2,1 ) cofact ( 2,2 ) cofact ( 2,3 )
cofact ( 3,1 ) cofact ( 3,2 ) cofact ( 3,3 ) ]T
= [−6 −2 3
−8 −2 4
8 2 −5 ]T
= [−6 −8 8
−2 −2 2
3 4 −5 ]
Hence, B−1 = Adj ( A )
Det ( A ) = −1
2 [−6 −8 8
−2 −2 2
3 4 −5 ] =
[ 3 4 −4
1 1 −1
−3
2 −2 5
2 ]
Question 8:
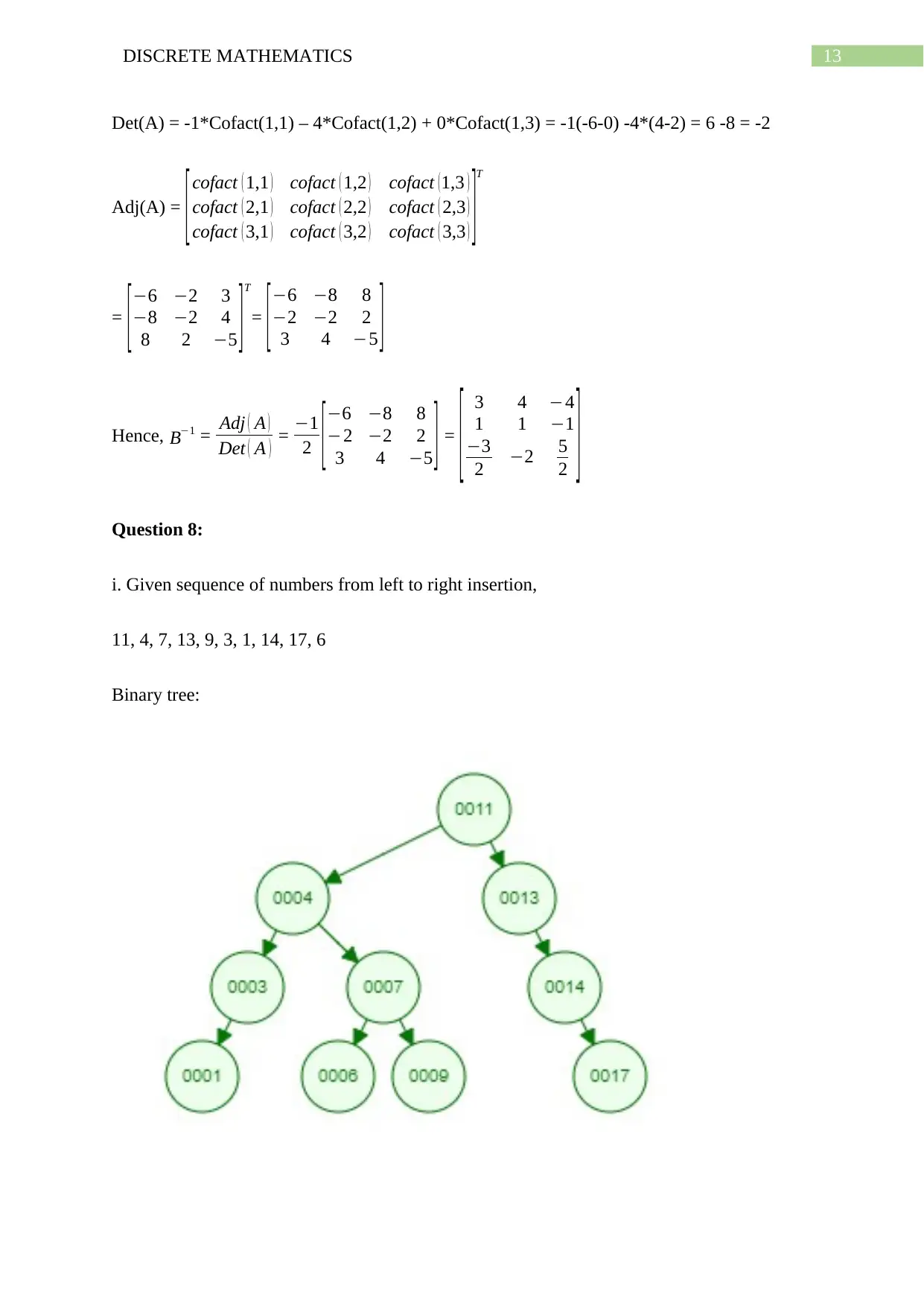
i. Given sequence of numbers from left to right insertion,
11, 4, 7, 13, 9, 3, 1, 14, 17, 6
Binary tree:
Det(A) = -1*Cofact(1,1) – 4*Cofact(1,2) + 0*Cofact(1,3) = -1(-6-0) -4*(4-2) = 6 -8 = -2
Adj(A) = [cofact ( 1,1 ) cofact ( 1,2 ) cofact (1,3 )
cofact ( 2,1 ) cofact ( 2,2 ) cofact ( 2,3 )
cofact ( 3,1 ) cofact ( 3,2 ) cofact ( 3,3 ) ]T
= [−6 −2 3
−8 −2 4
8 2 −5 ]T
= [−6 −8 8
−2 −2 2
3 4 −5 ]
Hence, B−1 = Adj ( A )
Det ( A ) = −1
2 [−6 −8 8
−2 −2 2
3 4 −5 ] =
[ 3 4 −4
1 1 −1
−3
2 −2 5
2 ]
Question 8:
i. Given sequence of numbers from left to right insertion,
11, 4, 7, 13, 9, 3, 1, 14, 17, 6
Binary tree:
14DISCRETE MATHEMATICS
Hence, by the binary tree the sorted sequence will be 1,3,4,6,7,9,11,13,14,17.
ii.
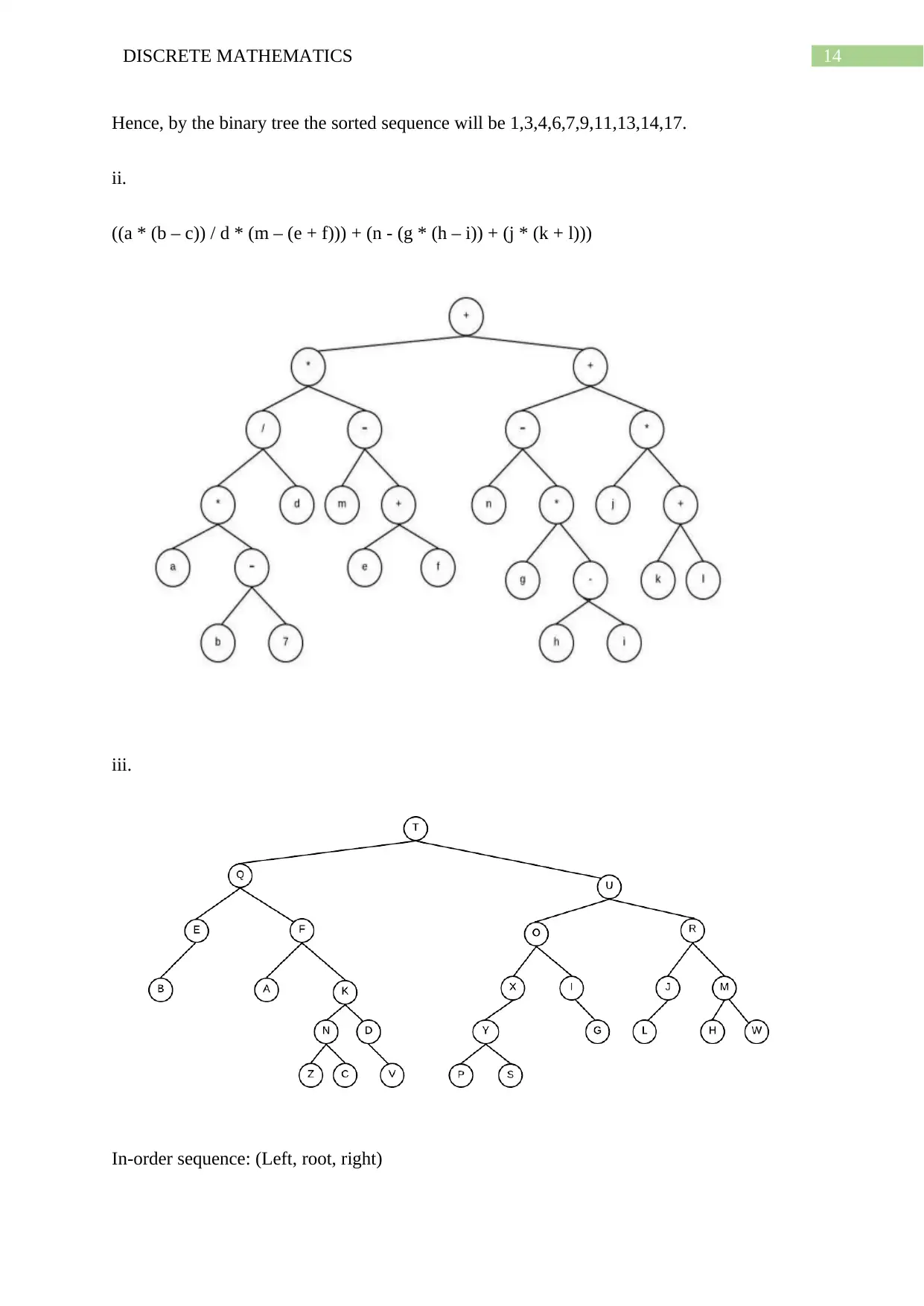
((a * (b – c)) / d * (m – (e + f))) + (n - (g * (h – i)) + (j * (k + l)))
iii.
In-order sequence: (Left, root, right)
Hence, by the binary tree the sorted sequence will be 1,3,4,6,7,9,11,13,14,17.
ii.
((a * (b – c)) / d * (m – (e + f))) + (n - (g * (h – i)) + (j * (k + l)))
iii.
In-order sequence: (Left, root, right)

15DISCRETE MATHEMATICS
Pre-order sequence: (Root, Left, Right)
Post-order sequence: (Left, Right, Root)
Post-order traversal sequence: ZCNVDAKEBFQPSYXGIOLJHWMRUT
Pre-order traversal sequence: TURMWHJLOIGXYSPQFBEKADVNCZ
In-order traversal sequence: BEQAFZNCKDVTPYSXOIULJRHMW
Question 9:
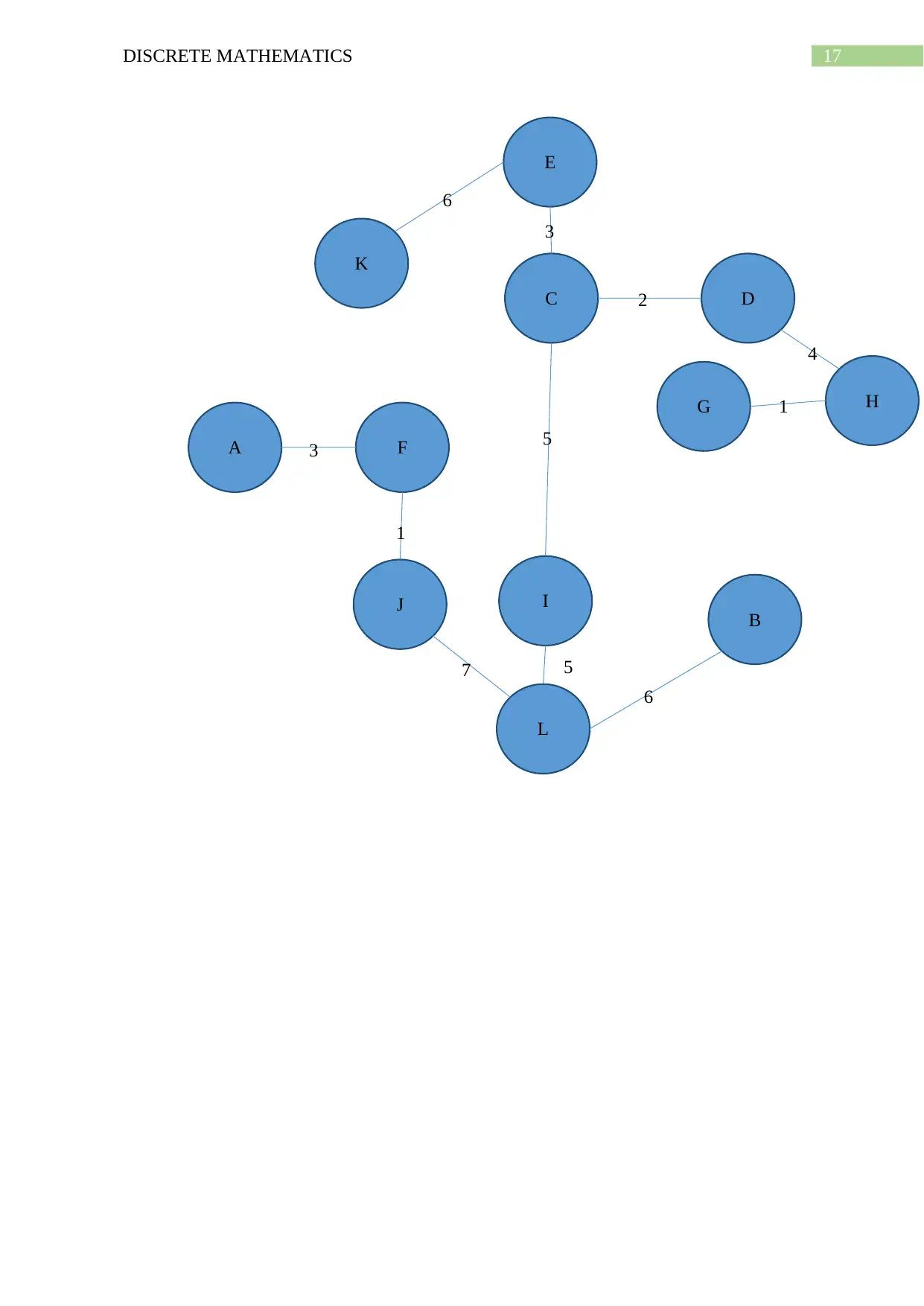
Given network,
By, Prim’s method the spanning tree construction in steps is shown below.
Pre-order sequence: (Root, Left, Right)
Post-order sequence: (Left, Right, Root)
Post-order traversal sequence: ZCNVDAKEBFQPSYXGIOLJHWMRUT
Pre-order traversal sequence: TURMWHJLOIGXYSPQFBEKADVNCZ
In-order traversal sequence: BEQAFZNCKDVTPYSXOIULJRHMW
Question 9:
Given network,
By, Prim’s method the spanning tree construction in steps is shown below.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
16DISCRETE MATHEMATICS
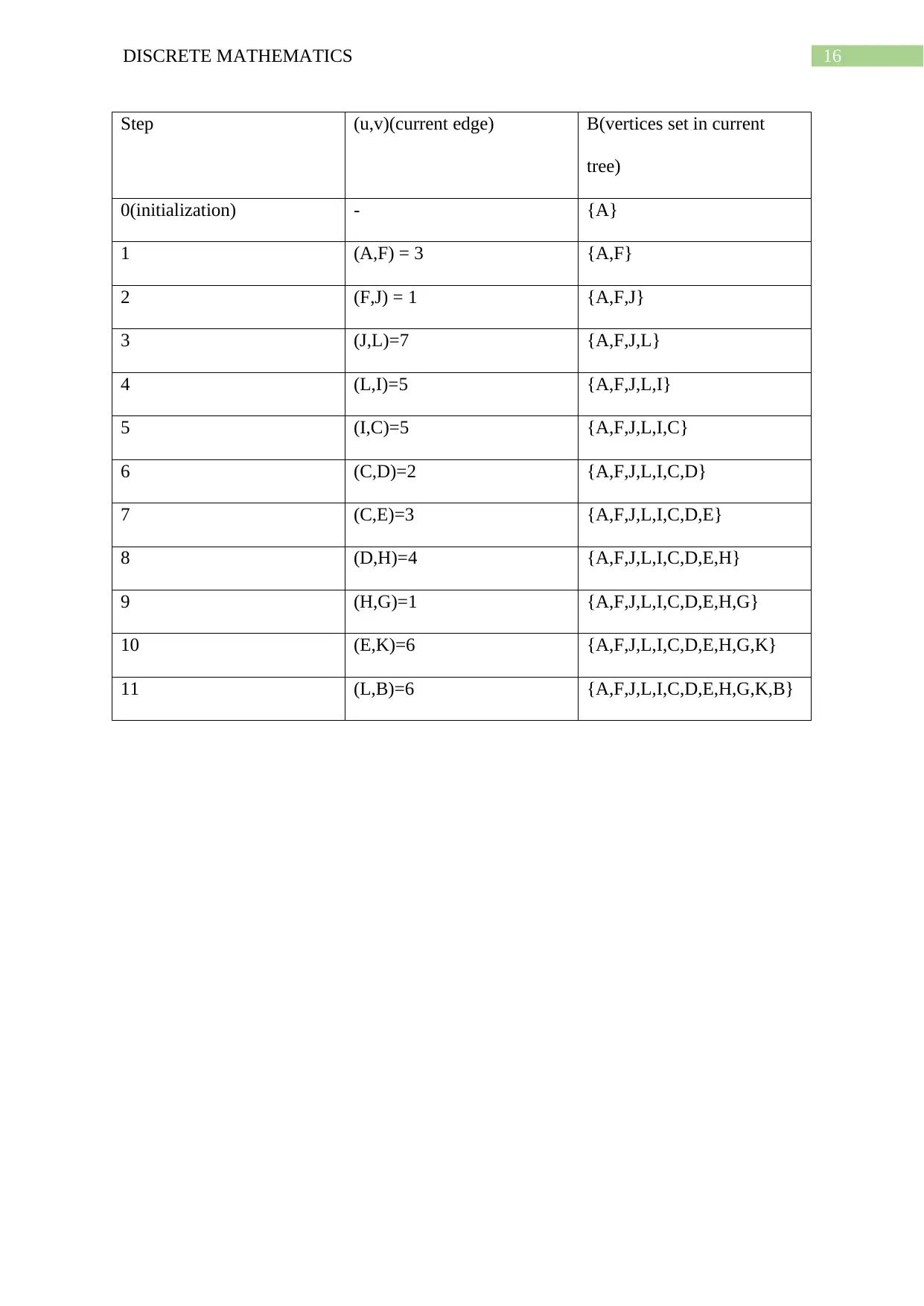
Step (u,v)(current edge) B(vertices set in current
tree)
0(initialization) - {A}
1 (A,F) = 3 {A,F}
2 (F,J) = 1 {A,F,J}
3 (J,L)=7 {A,F,J,L}
4 (L,I)=5 {A,F,J,L,I}
5 (I,C)=5 {A,F,J,L,I,C}
6 (C,D)=2 {A,F,J,L,I,C,D}
7 (C,E)=3 {A,F,J,L,I,C,D,E}
8 (D,H)=4 {A,F,J,L,I,C,D,E,H}
9 (H,G)=1 {A,F,J,L,I,C,D,E,H,G}
10 (E,K)=6 {A,F,J,L,I,C,D,E,H,G,K}
11 (L,B)=6 {A,F,J,L,I,C,D,E,H,G,K,B}
Step (u,v)(current edge) B(vertices set in current
tree)
0(initialization) - {A}
1 (A,F) = 3 {A,F}
2 (F,J) = 1 {A,F,J}
3 (J,L)=7 {A,F,J,L}
4 (L,I)=5 {A,F,J,L,I}
5 (I,C)=5 {A,F,J,L,I,C}
6 (C,D)=2 {A,F,J,L,I,C,D}
7 (C,E)=3 {A,F,J,L,I,C,D,E}
8 (D,H)=4 {A,F,J,L,I,C,D,E,H}
9 (H,G)=1 {A,F,J,L,I,C,D,E,H,G}
10 (E,K)=6 {A,F,J,L,I,C,D,E,H,G,K}
11 (L,B)=6 {A,F,J,L,I,C,D,E,H,G,K,B}
17DISCRETE MATHEMATICS
A F
J
3
1
L
7
I
5
C
5
D2
E
3
H
4
G 1
K
6
B
6
A F
J
3
1
L
7
I
5
C
5
D2
E
3
H
4
G 1
K
6
B
6

18DISCRETE MATHEMATICS
Hence, minimum cost of spanning tree = 3+1+7+5+5+2+3+4+1+6+6 = 43 meters.
Hence, the minimal cost in dollars = 43*$45= $1935.
The same spanning tree and same minimal cost can be obtained by Kruskal method also.
Question 10:
i.
The graph Y is given below.
As the Graph is undirected, hence each loop adds 1 to the diagonal entry and an edge adds 1
to the corresponding entry. The entries are row wise and column wise for A,B,C and D.
Hence, the adjacency matrix will be
[1 1 2 1
1 1 0 2
2 0 0 1
1 2 1 0 ]
ii. In the graph Y there are two walks from A to C that are of length 3.
Walk 1: A>B>D(1st parallel edge)>C
Walk 2: A>B>D(2nd parallel edge)>C
Hence, minimum cost of spanning tree = 3+1+7+5+5+2+3+4+1+6+6 = 43 meters.
Hence, the minimal cost in dollars = 43*$45= $1935.
The same spanning tree and same minimal cost can be obtained by Kruskal method also.
Question 10:
i.
The graph Y is given below.
As the Graph is undirected, hence each loop adds 1 to the diagonal entry and an edge adds 1
to the corresponding entry. The entries are row wise and column wise for A,B,C and D.
Hence, the adjacency matrix will be
[1 1 2 1
1 1 0 2
2 0 0 1
1 2 1 0 ]
ii. In the graph Y there are two walks from A to C that are of length 3.
Walk 1: A>B>D(1st parallel edge)>C
Walk 2: A>B>D(2nd parallel edge)>C
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

19DISCRETE MATHEMATICS
iii. As there are two self-loops and two edges between two pairs of vertices, hence the graph
is not a simple graph.
The order of the graph Y is its number of vertices and size of the graph is the number of
edges.
Hence, (Order,Size) = (V,E) = (4,9)
iii. As there are two self-loops and two edges between two pairs of vertices, hence the graph
is not a simple graph.
The order of the graph Y is its number of vertices and size of the graph is the number of
edges.
Hence, (Order,Size) = (V,E) = (4,9)
1 out of 20
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.
