Comprehensive Statistical Analysis of Smoking's Relationship to Cancer
VerifiedAdded on 2022/11/13
|9
|1785
|2
Report
AI Summary
This report presents a statistical analysis examining the correlation between cigarette smoking and several forms of cancer, including lung, bladder, kidney, and leukemia, using data from a publicly available source. The analysis incorporates both descriptive and inferential statistical techniques. Descriptive statistics, including mean, standard deviation, skewness, and kurtosis, are computed for each variable, and graphical representations such as box plots are used to visualize the data distribution and identify potential outliers. Scatter plots and correlation analyses are performed to assess the strength and direction of the linear relationships between the quantity of cigarettes smoked and the incidence of each cancer type. Furthermore, linear regression models are developed to predict cancer cases based on smoking habits. The findings indicate a significant positive correlation between smoking and lung, bladder, and kidney cancers, while the relationship with leukemia is found to be insignificant. The report concludes with a discussion of the implications of these findings and recommendations for further research, emphasizing the need for causal analysis to determine if smoking directly causes cancer.

Does smoking increase the chance of lung cancer along with other forms of cancer in the
U.S.?
Name:
Institution:
U.S.?
Name:
Institution:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Introduction
Researchers have pointed out that different factors are associated with lung cancer. CDC,
(2018) shows that there are several risk factors that increase the chances of getting cancer.
CDC has reported that cigarette smoking is attributed to cancer. They estimated that
approximately 80 percent to 90 percent of the deaths associated to lung cancer are connected
to cigarette smoking. It is estimated that cigarette has a mixture of more than 700, with 70 of
the chemicals known to be carcinogenic (CDC, 2018). Thus, this research is designed to use
the data from http://lib.stat.cmu.edu/DASL/Datafiles/cigcancerdat.html to analyze and
determine whether there exists a significant linear relationship between lung cancer among
other forms of cancer.
The analysis in this study will basically cover the two categories of statistics, both descriptive
and inferential statistics. In the descriptive part, the study will cover both ‘the numerical
descriptive’ and the graphical illustration of the data distribution. The inference will be made
at the level .05, and recommendations made for the findings.
Analysis section
Descriptive statistics for the numeric variables was carried out and the results are as follows:
Table 1: Descriptive Statistics: CIG, BLAD, LUNG, KID, LEUK
Variable Mean StDev Minimum Maximum Range Skewness Kurtosis
CIG 24.914 5.573 14.000 42.400 28.400 0.98 2.07
BLAD 4.121 0.965 2.860 6.540 3.680 0.36 -0.68
LUNG 19.653 4.228 12.010 27.270 15.260 -0.10 -0.95
KID 2.7945 0.5191 1.5900 4.3200 2.7300 0.12 0.90
LEUK 6.8298 0.6383 4.9000 8.2800 3.3800 -0.33 1.20
The summary table indicates that on average people have 24.914 cigarettes (SD = 5.573
cigars) (Lowry, 2014). The data show that cigarettes smoked ranges between a minimum of
14 and a maximum of 42.40 cigars. The distribution of this variable is as illustrated below.
Researchers have pointed out that different factors are associated with lung cancer. CDC,
(2018) shows that there are several risk factors that increase the chances of getting cancer.
CDC has reported that cigarette smoking is attributed to cancer. They estimated that
approximately 80 percent to 90 percent of the deaths associated to lung cancer are connected
to cigarette smoking. It is estimated that cigarette has a mixture of more than 700, with 70 of
the chemicals known to be carcinogenic (CDC, 2018). Thus, this research is designed to use
the data from http://lib.stat.cmu.edu/DASL/Datafiles/cigcancerdat.html to analyze and
determine whether there exists a significant linear relationship between lung cancer among
other forms of cancer.
The analysis in this study will basically cover the two categories of statistics, both descriptive
and inferential statistics. In the descriptive part, the study will cover both ‘the numerical
descriptive’ and the graphical illustration of the data distribution. The inference will be made
at the level .05, and recommendations made for the findings.
Analysis section
Descriptive statistics for the numeric variables was carried out and the results are as follows:
Table 1: Descriptive Statistics: CIG, BLAD, LUNG, KID, LEUK
Variable Mean StDev Minimum Maximum Range Skewness Kurtosis
CIG 24.914 5.573 14.000 42.400 28.400 0.98 2.07
BLAD 4.121 0.965 2.860 6.540 3.680 0.36 -0.68
LUNG 19.653 4.228 12.010 27.270 15.260 -0.10 -0.95
KID 2.7945 0.5191 1.5900 4.3200 2.7300 0.12 0.90
LEUK 6.8298 0.6383 4.9000 8.2800 3.3800 -0.33 1.20
The summary table indicates that on average people have 24.914 cigarettes (SD = 5.573
cigars) (Lowry, 2014). The data show that cigarettes smoked ranges between a minimum of
14 and a maximum of 42.40 cigars. The distribution of this variable is as illustrated below.

4236302418
12
10
8
6
4
2
0
CIG
Frequency
Histogram of CIG
45
40
35
30
25
20
15
10
CIG
Boxplot of CIG
The box plot indicates that there are two values that should be considered to be outliers. This
result suggests that the data will have a long tail to the higher value side, which is supported
by the values of skewness and kurtosis (Ott & Longnecker, 2015). However, the box plot is
symmetrical suggesting that the data might be from a normally distributed population.
From Table 1 shows that on average the bladder cancer is 4.121 (SD = 0.965) (Lowry, 2014).
The bladder cancer cases range between 2.860 and 6.540. The distribution of this variable is
as illustrated below.
6.56.05.55.04.54.03.53.0
12
10
8
6
4
2
0
BLAD
Frequency
Histogram of BLAD
7
6
5
4
3
BLAD
Boxplot of BLAD
The plot shows that the data are skewed to the right or they are positively skewed. However,
they do not have outliers. The skewness of the plot suggests that the data might not be
normally distributed.
12
10
8
6
4
2
0
CIG
Frequency
Histogram of CIG
45
40
35
30
25
20
15
10
CIG
Boxplot of CIG
The box plot indicates that there are two values that should be considered to be outliers. This
result suggests that the data will have a long tail to the higher value side, which is supported
by the values of skewness and kurtosis (Ott & Longnecker, 2015). However, the box plot is
symmetrical suggesting that the data might be from a normally distributed population.
From Table 1 shows that on average the bladder cancer is 4.121 (SD = 0.965) (Lowry, 2014).
The bladder cancer cases range between 2.860 and 6.540. The distribution of this variable is
as illustrated below.
6.56.05.55.04.54.03.53.0
12
10
8
6
4
2
0
BLAD
Frequency
Histogram of BLAD
7
6
5
4
3
BLAD
Boxplot of BLAD
The plot shows that the data are skewed to the right or they are positively skewed. However,
they do not have outliers. The skewness of the plot suggests that the data might not be
normally distributed.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

On average the lung cancer cases are 19.653 (SD = 4.228). The cases of lung cancer range
between 12.010 and 27.270. The distribution of lung cancer is illustrated below.
2824201612
9
8
7
6
5
4
3
2
1
0
LUNG
Frequency
Histogram of LUNG
28
26
24
22
20
18
16
14
12
10
LUNG
Boxplot of LUNG
The plot suggests that the lung cancer data are negatively skewed. The data do not have
outliers (Ott & Longnecker, 2015).
Scatter plot assessment
Correlation assessment was carried out between number of cigars and different forms of
cancers. First, the scatter plots were used to graphically illustrate the direction of the
relationship.
between 12.010 and 27.270. The distribution of lung cancer is illustrated below.
2824201612
9
8
7
6
5
4
3
2
1
0
LUNG
Frequency
Histogram of LUNG
28
26
24
22
20
18
16
14
12
10
LUNG
Boxplot of LUNG
The plot suggests that the lung cancer data are negatively skewed. The data do not have
outliers (Ott & Longnecker, 2015).
Scatter plot assessment
Correlation assessment was carried out between number of cigars and different forms of
cancers. First, the scatter plots were used to graphically illustrate the direction of the
relationship.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
40302010
30
20
10
0
40302010
30
20
10
0
BLAD
CIG
LUNG
KID LEUK
Scatterplot of BLAD, LUNG, KID, LEUK vs CIG
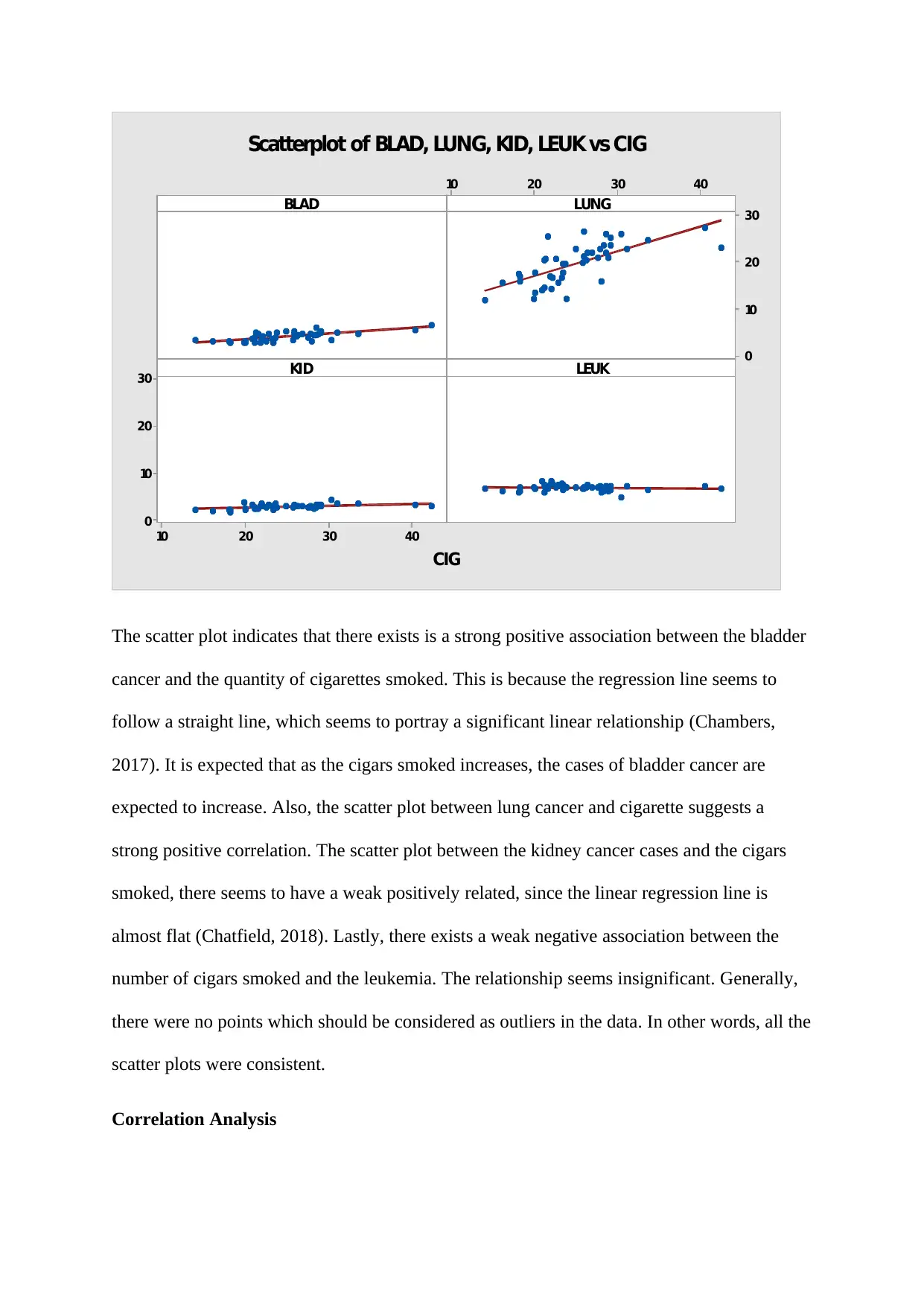
The scatter plot indicates that there exists is a strong positive association between the bladder
cancer and the quantity of cigarettes smoked. This is because the regression line seems to
follow a straight line, which seems to portray a significant linear relationship (Chambers,
2017). It is expected that as the cigars smoked increases, the cases of bladder cancer are
expected to increase. Also, the scatter plot between lung cancer and cigarette suggests a
strong positive correlation. The scatter plot between the kidney cancer cases and the cigars
smoked, there seems to have a weak positively related, since the linear regression line is
almost flat (Chatfield, 2018). Lastly, there exists a weak negative association between the
number of cigars smoked and the leukemia. The relationship seems insignificant. Generally,
there were no points which should be considered as outliers in the data. In other words, all the
scatter plots were consistent.
Correlation Analysis
30
20
10
0
40302010
30
20
10
0
BLAD
CIG
LUNG
KID LEUK
Scatterplot of BLAD, LUNG, KID, LEUK vs CIG
The scatter plot indicates that there exists is a strong positive association between the bladder
cancer and the quantity of cigarettes smoked. This is because the regression line seems to
follow a straight line, which seems to portray a significant linear relationship (Chambers,
2017). It is expected that as the cigars smoked increases, the cases of bladder cancer are
expected to increase. Also, the scatter plot between lung cancer and cigarette suggests a
strong positive correlation. The scatter plot between the kidney cancer cases and the cigars
smoked, there seems to have a weak positively related, since the linear regression line is
almost flat (Chatfield, 2018). Lastly, there exists a weak negative association between the
number of cigars smoked and the leukemia. The relationship seems insignificant. Generally,
there were no points which should be considered as outliers in the data. In other words, all the
scatter plots were consistent.
Correlation Analysis

Correlation analysis was carried out and the results are summarized in the correlation matrix
in Table 2.
Table 2: Correlation: BLAD, LUNG, KID, LEUK, CIG
BLAD LUNG KID LEUK
LUNG 0.659
0.000
KID 0.359 0.283
0.017 0.063
LEUK 0.162 -0.152 0.189
0.293 0.326 0.220
CIG 0.704 0.697 0.487 -0.068
0.000 0.000 0.001 0.659
Cell Contents: Pearson correlation
P-Value
Table 2 supports the scatter plot, which suggested existence of strong positive relationship
between the number of cigars smoked and bladder cancer (r (43) = 0.704, p-value < .05)
(Cohen, West, & Aiken, 2014). Thus, since the p-value is less than .05, we conclude that the
linear correlation between the quantity of cigarettes smoked and number of bladder cancer
cases is significant. Also, there is a strong significant relationship between the number of
cigarette smoked and lung cancer (r (43) = 0.697, p-value < .05). Also, although the
correlation coefficient between number of cigarette smoked and kidney cancer suggest a
moderate positive relationship, this correlation is significant (r (43) = 0.487, p-value < .05)
(Bland, 2015). Lastly but not least, there is no significant correlation between quantity of
cigarettes smoked and blood cancer (leukemia) (r (43) = -0.068, p-value = .695). Therefore,
there is no need to run a linear regression between the number of cigarette smoked and
leukemia.
Regression
We run a linear regression analysis of the different forms of cancer on quantity of cigarettes
smoked. Note that in this case, we are interested in predicting number cancer cases using the
number of cigars smoked. The hypothesis is that there is no linear relationship between the
in Table 2.
Table 2: Correlation: BLAD, LUNG, KID, LEUK, CIG
BLAD LUNG KID LEUK
LUNG 0.659
0.000
KID 0.359 0.283
0.017 0.063
LEUK 0.162 -0.152 0.189
0.293 0.326 0.220
CIG 0.704 0.697 0.487 -0.068
0.000 0.000 0.001 0.659
Cell Contents: Pearson correlation
P-Value
Table 2 supports the scatter plot, which suggested existence of strong positive relationship
between the number of cigars smoked and bladder cancer (r (43) = 0.704, p-value < .05)
(Cohen, West, & Aiken, 2014). Thus, since the p-value is less than .05, we conclude that the
linear correlation between the quantity of cigarettes smoked and number of bladder cancer
cases is significant. Also, there is a strong significant relationship between the number of
cigarette smoked and lung cancer (r (43) = 0.697, p-value < .05). Also, although the
correlation coefficient between number of cigarette smoked and kidney cancer suggest a
moderate positive relationship, this correlation is significant (r (43) = 0.487, p-value < .05)
(Bland, 2015). Lastly but not least, there is no significant correlation between quantity of
cigarettes smoked and blood cancer (leukemia) (r (43) = -0.068, p-value = .695). Therefore,
there is no need to run a linear regression between the number of cigarette smoked and
leukemia.
Regression
We run a linear regression analysis of the different forms of cancer on quantity of cigarettes
smoked. Note that in this case, we are interested in predicting number cancer cases using the
number of cigars smoked. The hypothesis is that there is no linear relationship between the
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

number of cigars smoked and different forms of cancer (Cohen, West, & Aiken, 2014). The
summary of the results is as follows.
Table 3: regression between bladder cancer and the number of cigarette smoked
Model Summary
S R-sq R-sq(adj) R-sq(pred)
0.693766 49.51% 48.31% 45.67%
Coefficients
Term Coef SE Coef T-Value P-Value VIF
Constant 1.086 0.484 2.24 0.030
CIG 0.1218 0.0190 6.42 0.000 1.00
Regression Equation
BLAD = 1.086 + 0.1218 CIG
The summary of the model indicates that the cigarette coefficient is significant (β = 0.1218, t
(42) = 6.42, p-value < .05) (Draper, 2014). The coefficient of determination indicates that the
model could account for 49.51% of sources of variation. Although this proportion of
variation is low, the model should be used in making predictions. A prediction was made for
the number of cases of bladder cancer when 24 cigarettes were smoked.
Variable Setting
CIG 24
Fit SE Fit 95% CI 95% PI
4.00978 0.106019 (3.79583, 4.22374) (2.59345, 5.42611)
Results indicate that on average 4.01 cases of lung cancer are expected.
The linear model between the quantity of cigarettes smoked and lung cancer is summarized
below.
Model Summary
S R-sq R-sq(adj) R-sq(pred)
3.06607 48.64% 47.41% 41.97%
Coefficients
Term Coef SE Coef T-Value P-Value VIF
Constant 6.47 2.14 3.02 0.004
CIG 0.5291 0.0839 6.31 0.000 1.00
summary of the results is as follows.
Table 3: regression between bladder cancer and the number of cigarette smoked
Model Summary
S R-sq R-sq(adj) R-sq(pred)
0.693766 49.51% 48.31% 45.67%
Coefficients
Term Coef SE Coef T-Value P-Value VIF
Constant 1.086 0.484 2.24 0.030
CIG 0.1218 0.0190 6.42 0.000 1.00
Regression Equation
BLAD = 1.086 + 0.1218 CIG
The summary of the model indicates that the cigarette coefficient is significant (β = 0.1218, t
(42) = 6.42, p-value < .05) (Draper, 2014). The coefficient of determination indicates that the
model could account for 49.51% of sources of variation. Although this proportion of
variation is low, the model should be used in making predictions. A prediction was made for
the number of cases of bladder cancer when 24 cigarettes were smoked.
Variable Setting
CIG 24
Fit SE Fit 95% CI 95% PI
4.00978 0.106019 (3.79583, 4.22374) (2.59345, 5.42611)
Results indicate that on average 4.01 cases of lung cancer are expected.
The linear model between the quantity of cigarettes smoked and lung cancer is summarized
below.
Model Summary
S R-sq R-sq(adj) R-sq(pred)
3.06607 48.64% 47.41% 41.97%
Coefficients
Term Coef SE Coef T-Value P-Value VIF
Constant 6.47 2.14 3.02 0.004
CIG 0.5291 0.0839 6.31 0.000 1.00
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Regression Equation
LUNG = 6.47 + 0.5291 CIG
There exists a significant linear association between the number of cigars smoked and lung
cancers cases (F (1, 42) = 39.77, p-value < .05) (Keller, 2015). This model can be used to
predict the lung cancer cases when the number of cigars smoked is known. In fact, this model
could account for 48.64% of sources of variation.
The for none significant model between leukemia and the number of cigarette smoked, we
just use the average number of cases of leukemia as predicted values.
Summary/conclusion
It was found that there was a linear relationship between these three forms of cancer (lung
cancer; bladder cancer; and kidney cancer) and the quantity of cigarettes an individual smoke.
The strongest relationship was found to be between the two forms of cancer (lung cancer and
kidney cancer) and the dependent variable (cigarettes smoked). Thus, it can be inferred that to
reduce cases of cancer, smoking cigarettes should be either regulated or abolished since they
are correlated with cancer. However, a causal analysis should be carried out since it might not
necessarily imply that smoking cigarettes cause cancer.
LUNG = 6.47 + 0.5291 CIG
There exists a significant linear association between the number of cigars smoked and lung
cancers cases (F (1, 42) = 39.77, p-value < .05) (Keller, 2015). This model can be used to
predict the lung cancer cases when the number of cigars smoked is known. In fact, this model
could account for 48.64% of sources of variation.
The for none significant model between leukemia and the number of cigarette smoked, we
just use the average number of cases of leukemia as predicted values.
Summary/conclusion
It was found that there was a linear relationship between these three forms of cancer (lung
cancer; bladder cancer; and kidney cancer) and the quantity of cigarettes an individual smoke.
The strongest relationship was found to be between the two forms of cancer (lung cancer and
kidney cancer) and the dependent variable (cigarettes smoked). Thus, it can be inferred that to
reduce cases of cancer, smoking cigarettes should be either regulated or abolished since they
are correlated with cancer. However, a causal analysis should be carried out since it might not
necessarily imply that smoking cigarettes cause cancer.

References
Bland, M. (2015). An introduction to medical statistics. Oxford University Press (UK).
CDC. (2018, July 19). Lung Cancer. Retrieved from What Are the Risk Factors for Lung
Cancer?: https://www.cdc.gov/cancer/lung/basic_info/risk_factors.htm
Chambers, J. M. (2017). Graphical Methods for Data Analysis: 0. Chapman and Hall/CRC.
Chatfield, C. (2018). Statistics for technology: a course in applied statistics (3rd Edition ed.).
New York: Routledge.
Cohen, P., West, S. G., & Aiken, L. S. (2014). Applied multiple regression/correlation
analysis for the behavioral sciences (2nd ed.). Psychology Press.
Draper, N. R. (2014). Applied regression analysis. (Vol. 326). John Wiley & Sons.
Keller, G. (2015). Statistics for Management and Economics, Abbreviated. Cengage
Learning.
Lowry, R. (2014). Concepts and applications of inferential statistics.
Ott, R. L., & Longnecker, M. T. (2015). An introduction to statistical methods and data
analysis. Nelson Education.
Bland, M. (2015). An introduction to medical statistics. Oxford University Press (UK).
CDC. (2018, July 19). Lung Cancer. Retrieved from What Are the Risk Factors for Lung
Cancer?: https://www.cdc.gov/cancer/lung/basic_info/risk_factors.htm
Chambers, J. M. (2017). Graphical Methods for Data Analysis: 0. Chapman and Hall/CRC.
Chatfield, C. (2018). Statistics for technology: a course in applied statistics (3rd Edition ed.).
New York: Routledge.
Cohen, P., West, S. G., & Aiken, L. S. (2014). Applied multiple regression/correlation
analysis for the behavioral sciences (2nd ed.). Psychology Press.
Draper, N. R. (2014). Applied regression analysis. (Vol. 326). John Wiley & Sons.
Keller, G. (2015). Statistics for Management and Economics, Abbreviated. Cengage
Learning.
Lowry, R. (2014). Concepts and applications of inferential statistics.
Ott, R. L., & Longnecker, M. T. (2015). An introduction to statistical methods and data
analysis. Nelson Education.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

