Sizing Ducts and Variable Speed Fan for Ventilation System

This article explains how to size ducts and variable speed fan for a ventilation system using the pressure drop method and fan characteristics. It includes calculations for finding the operating point, speed, power, and efficiency of the fan. The article also discusses the assumptions made in the calculations and the importance of including dampers for effective control.

SOLUTIONS TO THE QUESTIONS
1. In this question, we shall use The Pressure Drop Method to size the ducts as given in the
ventilation system illustrated:
Table 1: The pressure drops for the silencers
Face
velocity(m/s)
2 2.5 3.0 3.5 4.0 5.0
Pressure
drop (Pa)
2 3 4 6 8 12
Firstly, we use the continuity equation which is based on mass conservation to determine
the flow rates in each ducting:
The flow rate Q= Uab xAab
But since it is a circular one, the duct size (diameter) is obtained using the formula:
d2 = 4Qab/πUab…..(1)
d= (4x2.5/πx5)0.5= 0.7979 approximately d= 0.8m
Then we can now use the chart in Appendix from the course book, we read off the
velocity and duct size by considering the flow rate and pressure drop.
But firstly we will establish the common pressure drop in the entire system that will be
used as a basis for finding the missing parameters at every designated point within the
system:
And this is found as: P/l = 0.35
And then we can turn back to the individual ducts to size them using the mentioned chart
hence table 1 provides the approximated values for velocity and duct size.
Table 1: Duct Sizing
DUCT FLOW RATE
Q(m3/s)
VELOCITY U(m/s) Duct size (m)
H-7 0.4 3.2 0.4
H-6 0.4 3.2 0.4
B-H 0.4+0.4+0.4=1.2 4.1 0.6
E-3 0.3 3.1 0.35
E-4 0.4 3.2 0.4
D-E 0.4+0.3=0.7 3.8 0.5
C-D 0.3+0.7=1.0 4.0 0.58
C-1 0.3 3.0 0.35

B-C 0.3+1.0=1.3 4.2 0.6
S2a-B 1.3+1.2=2.5 5.0 0.8
F2-S1(a) 2.5 5.0 0.8
F1-S1(b) 2.5 5.0 0.8
A-S1(a) 2.5 5.0 0.8
ASSUMPTIONS
We assume the following for the above case:
(i) The maximum velocity in main duct AB is fixed at 5m/s
(ii) The duct sizes of F2-S1, F1-S1, A-S1, S2(a)-B are diametrically equal
(iii) The pressure drops in the silencers and fan are balanced by the frictional factor
hence in the calculation, pressure drops for the silencers have not been considered
(iv) To improve performance and ensure that the system operates optimally, we will
need to include dampers to provide effective control
(v) There are no flow losses in the silencer and fan
Balancing the system Pressure drop:
Considering duct B-H:
The equivalent length, Le= 3+2+2+2+15+1.5=25.5m
Pb-h= Le(P/Le)=25.5 x 0.35= 8.925Pa
Now, considering duct B-E
Equivalent length Le= 2+1.5+2+1.5+2+1.5+2= 12.5
Pb-e= 12.5 x 0.35= 4.375Pa
It is clear that B-H has higher losses than B-E
Hence a damper is added to equalize the pressures between duct branches B-H and B-E
(Damper) Pb-e= Pb-h –Pb-e = 8.925- 4.375= 4.55 Pa

2. In this question, we consider a variable speed fan which is used to supply the air for the
ventilation system. The characteristics for the fan, in terms of total pressure, for a speed
of 1000 r.p.m., are given in Table 1 below.
Table 2: Fan characteristics at 1000rpm
Flow rate Total Fan Pressure Fan Efficiency (%)
Q Pt n
0.5 110 40
1.0 115 60
1.5 115 75
2.0 107 82
2.5 95 82
3.0 75 75
3.5 55 62
4.0 35 40
Hence the following are determined from the given data:
(i) Calculating the speed at which the fan should operate in order to deliver the
required volume flow rates.
The system fan supplies air to six outlet ducts as shown in the illustrated
schematic. The total volume flow rate in the given system is computed using
continuity equation hence:
Q = 0.4+0.4+0.4+0.7+0.3+0.3 = 2.5 m3/s
Next, we calculate speed and power by considering the total pressure drops in the
system:
∆Pt = ρghL
= ρg [Frictional loss + Specific loss]
= ρg [
u2
2 g [ 4 f 1 L
de
+∑ K ] ]
Where:
ρ = density of air = 1.225 kg/m3
g = acceleration due to gravity = 9.81 m/s2
hL = head loss, m
u = velocity, m/s
de= equivalent diameter
K = loss coefficient

We use chart 1 from the appendix course book to determine the pressure loss due
to friction is determined from chart1 and pressure loss due to specific losses is
calculated by finding relevant K value from CIBSE Guide tables and substituting
in the above formula.
This is done by considering each section pressure loss in the system:
(1) Pressure loss from point (B) to E-4:
(i) Pressure loss at exit of silencer 2:
Given,
A1 = π/4d2= 3.142/4 x 0.62= 0.2828m2
A2 = 3.142x0.52= 0.7855m2
A1/A2= 0.2828/0.7855 = 0.3600
θ1 = 45°, θ2 = 45°
θ = θ1 + θ2 = 90°
From CIBSE Guide C Table C4.80 (SMACNA):
For A2/A1 = 0.36 & θ = 180°; Loss Coefficient K = 0.135
Pressure loss from point at the entrance of duct (B) =
ρu2
2 x ∑ K
= 1.225x4.12/2 x 0.135= 1.389Pa
(ii) Pressure loss in duct B to C:
Given K = 0.45
Pressure loss =
ρu2
2 x ∑ K
= 1.225x4.22/2 x 0.45= 4.862Pa
(iii) Pressure loss in Silencer 2:
We check its velocity given the average pressure drop, u=3.0m/s
Pressure loss = (2+3+4+6+8+12)/6= 5.833
(iv) Pressure loss in Silencer 1:
We assume the same pressure drop as silencer 2 hence:
Pressure loss= 5.833
(v) Pressure loss in Fan:
Length: L = 1+ 1.5 = 2.5 m
For Q= 2.5m3/s & u = 5.0 m/s;
Pressure loss due to friction is given by:

∆P/L = 1.3 Pa/m (from chart1)
∆P = 1.3 x 0.35= 0.455Pa
(vi) Pressure loss in duct outlets:
Outlet 1:
Effective length, l= 1m and Q= 0.3m3/s, u= 3.0m/s
P=1 x 0.35= 0.35Pa
Outlet 2:
Effective length, l= 1m and Q= 0.3m3/s, u= 3.0m/s
P=1 x 0.35= 0.35Pa
Outlet 3:
Effective length, l= 1m and Q= 0.3m3/s, u= 3.0m/s
P=1 x 0.35= 0.35Pa
(2) Pressure loss in Duct branch B-H:
(i) Pressure loss in the straight duct B to the corner:
Effective length, le = 3+2+2+2+1.5+1.5= 12m
For velocity u = 4.1 m/s;
∆P = 0.35x 12= 4.2Pa (from given data)
(ii) Pressure loss at the corner
Length: L = 3m, Q = 1.2 m3/s & u = 4.1 m/s
∆P/L = 1.3 Pa/m (from chart1)
∆P = 1.3 x 0.35x3 = 1.365 Pa
(ii) Pressure loss at the Junction to 5:
Length: L = 11m, Q = 1.2 m3/s & u = 4.1 m/s
∆P/L = 1.3 Pa/m (from chart1)
∆P = 1.3 x 0.35x 11 = 5.005 Pa
(iii) Pressure loss at the outlets:
Outlet 5:
Effective length, l= 1.5m and Q= 0.4m3/s,

P=1 x 0.35x1.5= 0.525Pa
Outlet 6:
Effective length, l= 1.5m and Q= 0.4m3/s,
P=1 x 0.35x1.5= 0.525Pa
Outlet 7:
Effective length, l= 1m and Q= 0.3m3/s, u= 3.0m/s
P=1 x 0.35= 0.35Pa
Total Pressure loss in the system = 1.389+4.862+5.833+5.833+
0.455+0.35x3+4.2+1.365+5.005+ (0.525x3)
= 31.567 Pa
To find the speed & power of the fan to meet the design conditions
We have ∆Pt α Q2
∆Pt = K Q2
Where K is the system resistance
K = ∆Pt / Q2 = 31.567/ (1.52) =14.0298
Table 3: Fan characteristics at 1000rpm
Flow rate Q Total Fan
Pressure
Fan Efficiency
(%)
System
Pressure
0 0 0 0
0.5 110 40 3.50745
1.0 115 60 14.0298
1.5 115 75 21.0447
2.0 107 82 28.0596
2.5 95 82 35.0745
3.0 75 75 42.0894
3.5 55 62 49.1043
4.0 35 40 56.1192
From the above table, we plot the system characteristics which is actually Flow rate Q (x-axis),
Pt and Fan efficiency, system pressure (on the y-axis):

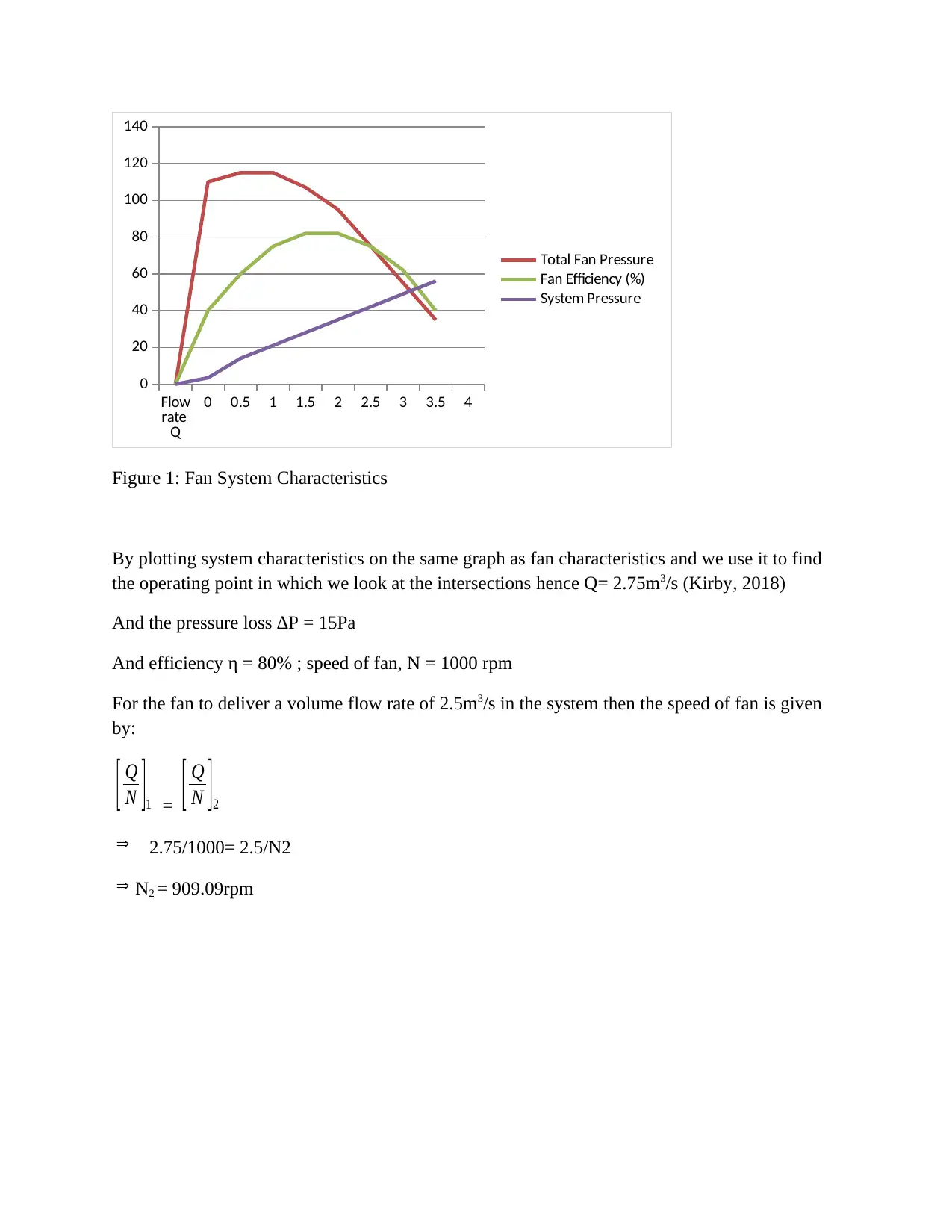
Flow
rate
Q
0 0.5 1 1.5 2 2.5 3 3.5 4
0
20
40
60
80
100
120
140
Total Fan Pressure
Fan Efficiency (%)
System Pressure
Figure 1: Fan System Characteristics
By plotting system characteristics on the same graph as fan characteristics and we use it to find
the operating point in which we look at the intersections hence Q= 2.75m3/s (Kirby, 2018)
And the pressure loss ∆P = 15Pa
And efficiency η = 80% ; speed of fan, N = 1000 rpm
For the fan to deliver a volume flow rate of 2.5m3/s in the system then the speed of fan is given
by:
[ Q
N ]1 = [ Q
N ]2
⇒ 2.75/1000= 2.5/N2
⇒ N2 = 909.09rpm

(iv) Calculating the power required by the fan.
Now for the speed of fan N2 = 909.09 the pressure drop across the fan is given by the relation:
[ ΔP
N2 ] 1
= [ ΔP
N 2 ]2
75/10002= P2/909.092
P2= 75x (909.092/10002)= 61.9833
To find the fan power (P) we have the following relationship:
P= QP2/n= 2.75x61.9833/0.8 = 213.0678 W
P= 0.2130678kW
Assumptions made during calculations.
-Frictional factor in the system was assumed to be balanced by the silencer and fan pressure
drops
-The fan system was assumed to be operating at a constant temperature
-Losses due to leakage were never considered in the calculation
Action taken to improve the design of the system:
-Minimizing losses by ensuring a more effective matching between system characteristic and fan
characteristics
-Deployment of energy efficiency strategies such as renewable energy use like solar PV in place
of generators for powering
- Installing a variable ventilation system such that during demand period, the performance is self-
excited to peak and declines in less demanding situations within the day; one way is to have an
automatic air inlet system that self-regulates the air inflow
-A properly instituted preventive maintenance program need to be established such that all the
components within the system are regularly inspected for reliability hence otherwise referred to
as reliability-centered maintenance.

-A huge chunk of costs normally comes from running of the plant; it is crucial that continuous
energy audits be performed to ascertain the energy cost vis-à-vis performance in the building
-Although the design of the ducts has been done, the design needs to be optimized so that
transmission losses are minimized. For Example, we can check the number of bends and let them
be brought down to a minimum number that optimizes the ventilation performance
-Furthermore, the HVAC system engineer or technician will have to monitor and assess the
performance of the system in and around all the designated rooms; in case, the performance is
poor, he/she must undertake the system redesign. Common cause for this, according to Winter
(2009), is often the presence of unsealed ducts which then attracts losses along the distribution
channel.
REFERENCE
Kirby ,R. (2018). Building Services Engineering Programme. Revised : Dr C König. Department
of Mechanical Engineering: Brunel University London.
Winter, S. (2009). ImprovingVentilation in Existing or New Buildings with Central Roof
Exhaust. National Center for Healthy Housing.