ECON 5313: Decisions and Strategies - Module 7 Homework

This homework includes solved problems on the market for health insurance, Market for Lemons experiment, and Principal Agent experiment with asymmetric information for ECON 5313: Decisions and Strategies - Module 7. The market for health insurance problem involves determining who will buy and won’t buy at different premiums and finding the insurer’s revenue, expenses, and profit at each premium. The Market for Lemons experiment problem involves analyzing the average seller value and evidence of adverse selection. The Principal Agent experiment with asymmetric information problem involves finding the minimum bonus that will induce the worker to exert high effort and determining if the boss’s payoff will be higher under high effort than under low effort.

ECON 5313: Decisions and Strategies
Module 7 Homework
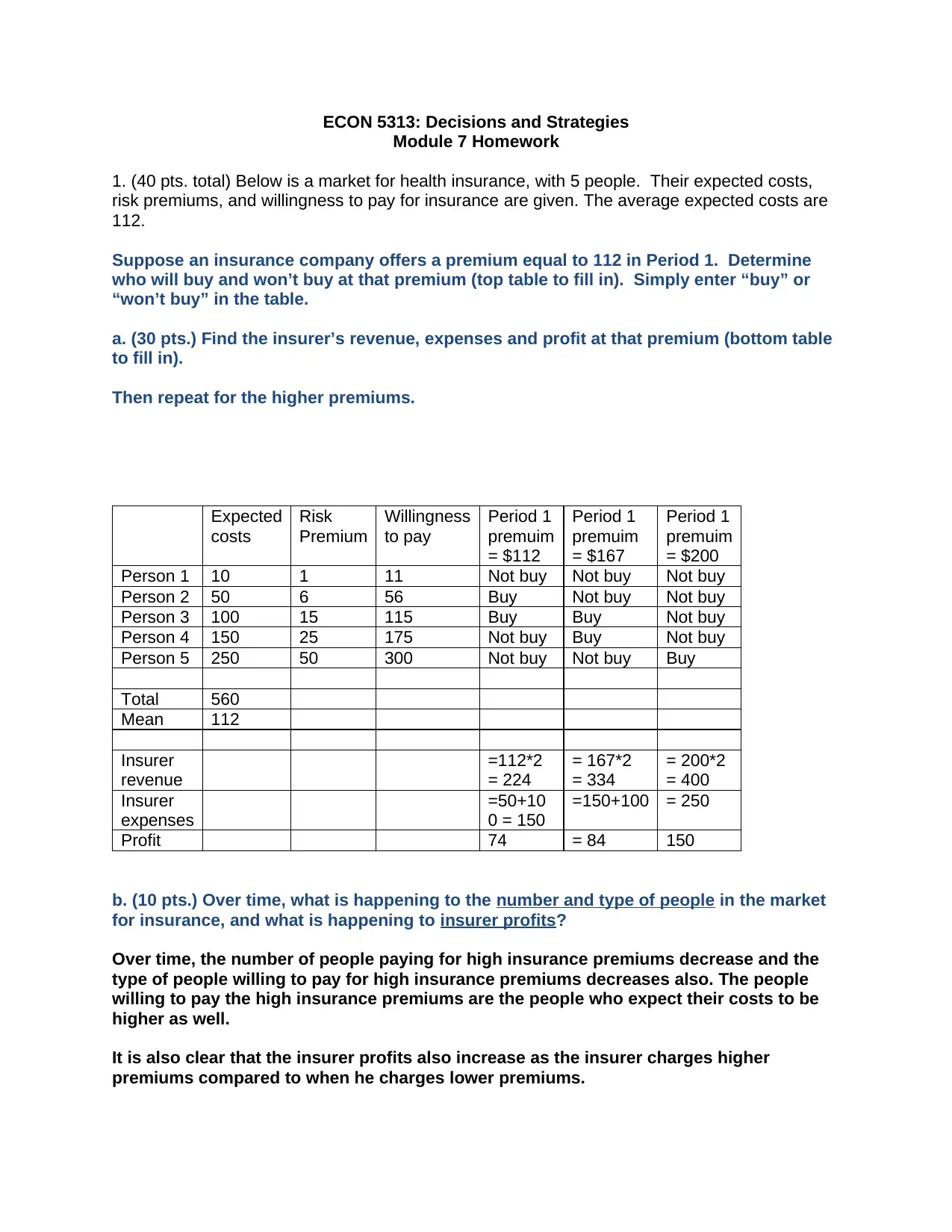
1. (40 pts. total) Below is a market for health insurance, with 5 people. Their expected costs,
risk premiums, and willingness to pay for insurance are given. The average expected costs are
112.
Suppose an insurance company offers a premium equal to 112 in Period 1. Determine
who will buy and won’t buy at that premium (top table to fill in). Simply enter “buy” or
“won’t buy” in the table.
a. (30 pts.) Find the insurer’s revenue, expenses and profit at that premium (bottom table
to fill in).
Then repeat for the higher premiums.
Expected
costs
Risk
Premium
Willingness
to pay
Period 1
premuim
= $112
Period 1
premuim
= $167
Period 1
premuim
= $200
Person 1 10 1 11 Not buy Not buy Not buy
Person 2 50 6 56 Buy Not buy Not buy
Person 3 100 15 115 Buy Buy Not buy
Person 4 150 25 175 Not buy Buy Not buy
Person 5 250 50 300 Not buy Not buy Buy
Total 560
Mean 112
Insurer
revenue
=112*2
= 224
= 167*2
= 334
= 200*2
= 400
Insurer
expenses
=50+10
0 = 150
=150+100 = 250
Profit 74 = 84 150
b. (10 pts.) Over time, what is happening to the number and type of people in the market
for insurance, and what is happening to insurer profits?
Over time, the number of people paying for high insurance premiums decrease and the
type of people willing to pay for high insurance premiums decreases also. The people
willing to pay the high insurance premiums are the people who expect their costs to be
higher as well.
It is also clear that the insurer profits also increase as the insurer charges higher
premiums compared to when he charges lower premiums.

2. (30 pts. Total) This problem is based on the Market for Lemons experiment.
The below table is based on almost 400 pairings that occurred in the experiment in a previous
semester. In some pairings, a transaction occurred (used car was sold), and in some pairings
no transaction occurred.
Average Seller Value (No Transaction) 3,022.42
Average Seller Value (Transaction) 2,511.89
a. (10 pts.) Based on the table above showing the average seller value in each case, is
there evidence of adverse selection? Explain.
Yes. In the case where the transaction occurred relating the sale of the used cars the
price was lower than where no transaction occurred. This is because, since the sellers
are selling used cars with no observable product quality, they provide low quality ued
cars to the buyers. Since the buyers expect low quality products from the sellers, they
are willing to pay less for the used car to protect themselves from risk of low quality
cars. In order for the sellers to protect themselves from lower quality, they sell lower
quality cars. The lower prices show the prices that the customers are willing to pay for
the expected low quality of cars they expect from the seller.
b. (10 pts.) Circle/highlight one and explain your answer. In the Market for Lemons experiment,
the role of the car seller is analogous to the role of the insurer / consumer in the insurance
example in #1.
Explain: In both cases, the consumer has more information about the product compared
to the insurer. In the case of insurance, the consumer of insurance, has more
information, about their own health compared to the insurer, therefore the insurer may be
in risk of experiencing more claims for a lower premium and therefore has to find a way
to mitigating those risks similarly to a car buyer who has less information about a car
compared to the car seller.
c. (10 pts.) Circle/highlight one and explain your answer. In the Market for Lemons experiment,
the role of the car buyer is analogous to the role of the insurer / consumer in the insurance
example in #1.
Explain: In both cases, the car buyer and the insurer have less information than the car
seller or the consumer of insurance. The insurer may expose themselves to risk if they
receive a lower premium for a high-risk insurance consumer. Similarly, a car buyer may

incur much loss if they purchase a car for a higher value than its quality and then not
long down the road, it breaks down.
3. (30 pts. total + Bonus) In the Principal Agent experiment with asymmetric information,
expected payoffs for the risky project are as follows (where RS equals revenue if successful, RU
equals revenue if unsuccessful, w equals wage, b equals bonus, p equals the probability of
success, e_H equals the cost of high effort and e_L equals the cost of low effort):
Boss (if worker chooses high effort): p*(RS) + (1-p)*(RU) - w - p*b
Boss (if worker chooses low effort): RU - w
Worker (if worker chooses high effort): w + p*b - e_H
Worker (if worker chooses low effort): w - e_L
Suppose:
RS = 800
RU = 200
p = 0.5
e_H = 100
e_L = 50
a. (15 pts.) What minimum bonus will induce the worker to exert high effort?
Expected payoff = w+ (0.5*b) – 100
0.5b = Expected payoff +100 -w
b >= (Expected payoff + 100 – w)/0.5
b >= (Expected payoff – w)/0.5 +20
b. (15 pts.) At the minimum bonus amount, will the boss’s payoff be higher under high effort
than under low effort? Show work to get credit.
Expected payoff = p*(RS) + (1-p)*(RU) - w - p*b
Expected payoff = 0.5(800) + (0.5*200) – w – p*b
Expected payoff = 400 + 100 – w – p*b
Expected payoff = 500 – w – 0.5(Expected payoff – w)/0.5 +20
Expected payoff = 500 – w – Expected payoff – w +20
2 Expected payoff = 500 + 20
2 Expected payoff = 520
Expected payoff = 260
Under low effort = 200 – w
Yes the boss’ payoff will be higher under high effort than under low effort since at high
effort the expected payoff is >=260 while at low effort expected payoff is 200 - w

c. (10 pts.) Bonus: What range of bonus amount will both induce high effort from the worker and
ensure the boss is better off than under low effort? Show all work to get credit.
If expected payoff is 260
260 = 0.5(800) + (0.5*200) – w – p*b
260 = 400 + 100 – w – 0.5b
260 = 500 – w – 0.5b
0.5b = 500 – 260 – w
0.5 b = (240 – w)
b = 120 – w/2
Range is 120 – w/2 =< b > = (Expected payoff – w)/0.5 +20