ECON634: Macquarie University Econometrics Take-home Test Solutions
VerifiedAdded on 2023/06/04
|14
|1832
|429
Homework Assignment
AI Summary
This document presents solutions to the ECON634 Econometrics and Business Statistics take-home test from Semester 2, 2018. The solutions cover various statistical concepts including hypothesis testing, confidence intervals, and regression analysis. The test assesses the application of these concept...

13
Econometrics and Business Statistics (ECON634)
Semester 2, 2018
Take-home Test
Econometrics and Business Statistics (ECON634)
Semester 2, 2018
Take-home Test
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
13
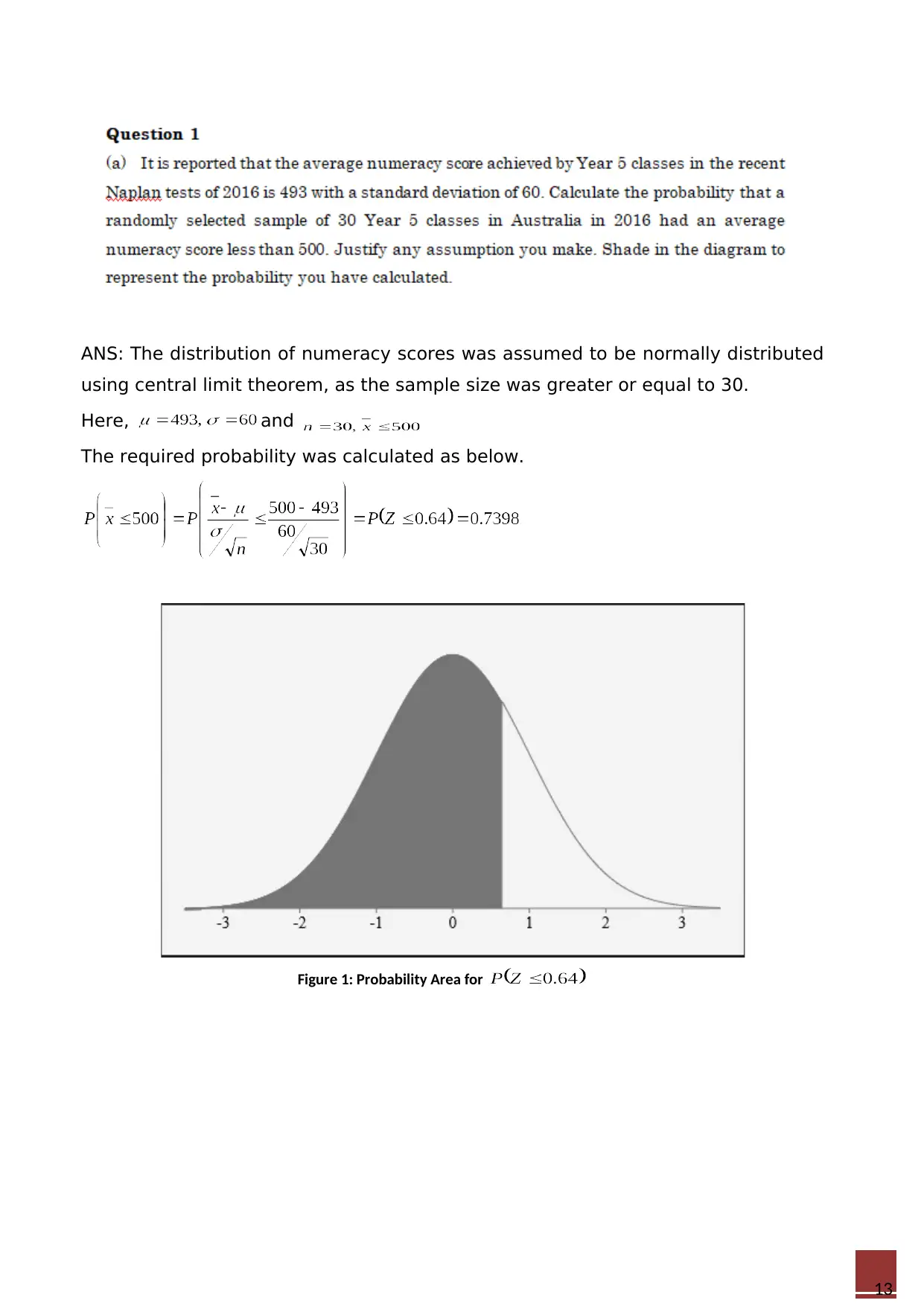
ANS: The distribution of numeracy scores was assumed to be normally distributed
using central limit theorem, as the sample size was greater or equal to 30.
Here, and
The required probability was calculated as below.
Figure 1: Probability Area for
ANS: The distribution of numeracy scores was assumed to be normally distributed
using central limit theorem, as the sample size was greater or equal to 30.
Here, and
The required probability was calculated as below.
Figure 1: Probability Area for
13
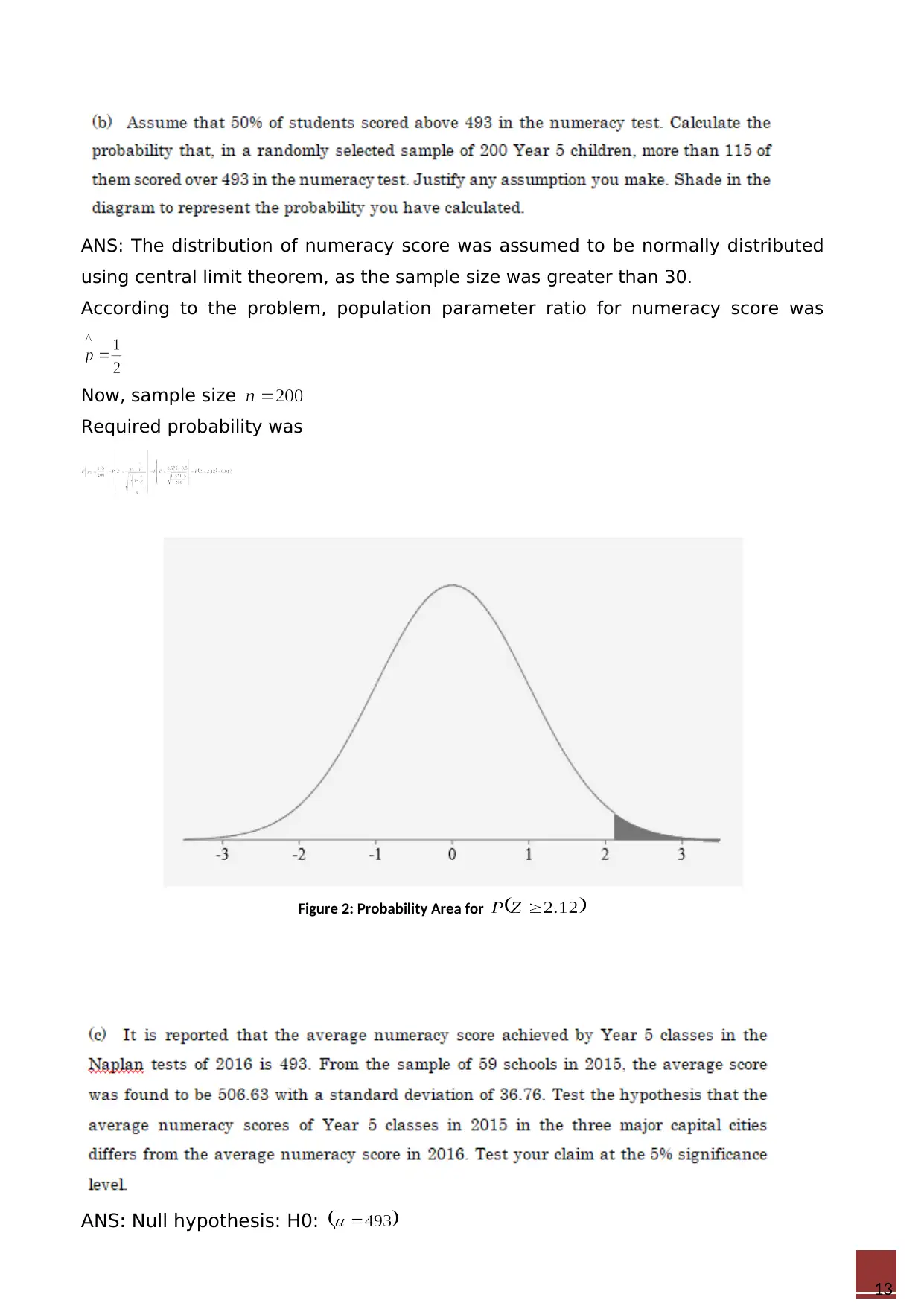
ANS: The distribution of numeracy score was assumed to be normally distributed
using central limit theorem, as the sample size was greater than 30.
According to the problem, population parameter ratio for numeracy score was
Now, sample size
Required probability was
Figure 2: Probability Area for
ANS: Null hypothesis: H0:
ANS: The distribution of numeracy score was assumed to be normally distributed
using central limit theorem, as the sample size was greater than 30.
According to the problem, population parameter ratio for numeracy score was
Now, sample size
Required probability was
Figure 2: Probability Area for
ANS: Null hypothesis: H0:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

13
Alternate Hypothesis: HA: where was the average numeracy score
achieved by Year 5 classes.
Level of significance was considered at 5%, and the test was a two tail test.
Sample statistic values were
Due to absence of population standard deviation, t-test was the appropriate
choice.
The t-statistic = with 58 degrees of freedom.
The p-value was < 0.05, at 5% level.
The 95% confidence interval for population mean was estimated as
, and the population average was
outside the interval.
Hence, the null hypothesis was rejected at 5% level of significance, concluding
that average numeracy scores in the three major capital cities were
significantly different from the average numeracy score of 493.
ANS: The 95% confidence interval for average numeracy score of all grade 5
classes in the major capital cities in 2015 was estimated as
, and the population average was
found to be outside the interval. Hence, the null hypothesis was correctly
rejected at 5% level of significance.
ANS: Null hypothesis: H0:
Alternate Hypothesis: HA:
Alternate Hypothesis: HA: where was the average numeracy score
achieved by Year 5 classes.
Level of significance was considered at 5%, and the test was a two tail test.
Sample statistic values were
Due to absence of population standard deviation, t-test was the appropriate
choice.
The t-statistic = with 58 degrees of freedom.
The p-value was < 0.05, at 5% level.
The 95% confidence interval for population mean was estimated as
, and the population average was
outside the interval.
Hence, the null hypothesis was rejected at 5% level of significance, concluding
that average numeracy scores in the three major capital cities were
significantly different from the average numeracy score of 493.
ANS: The 95% confidence interval for average numeracy score of all grade 5
classes in the major capital cities in 2015 was estimated as
, and the population average was
found to be outside the interval. Hence, the null hypothesis was correctly
rejected at 5% level of significance.
ANS: Null hypothesis: H0:
Alternate Hypothesis: HA:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
13
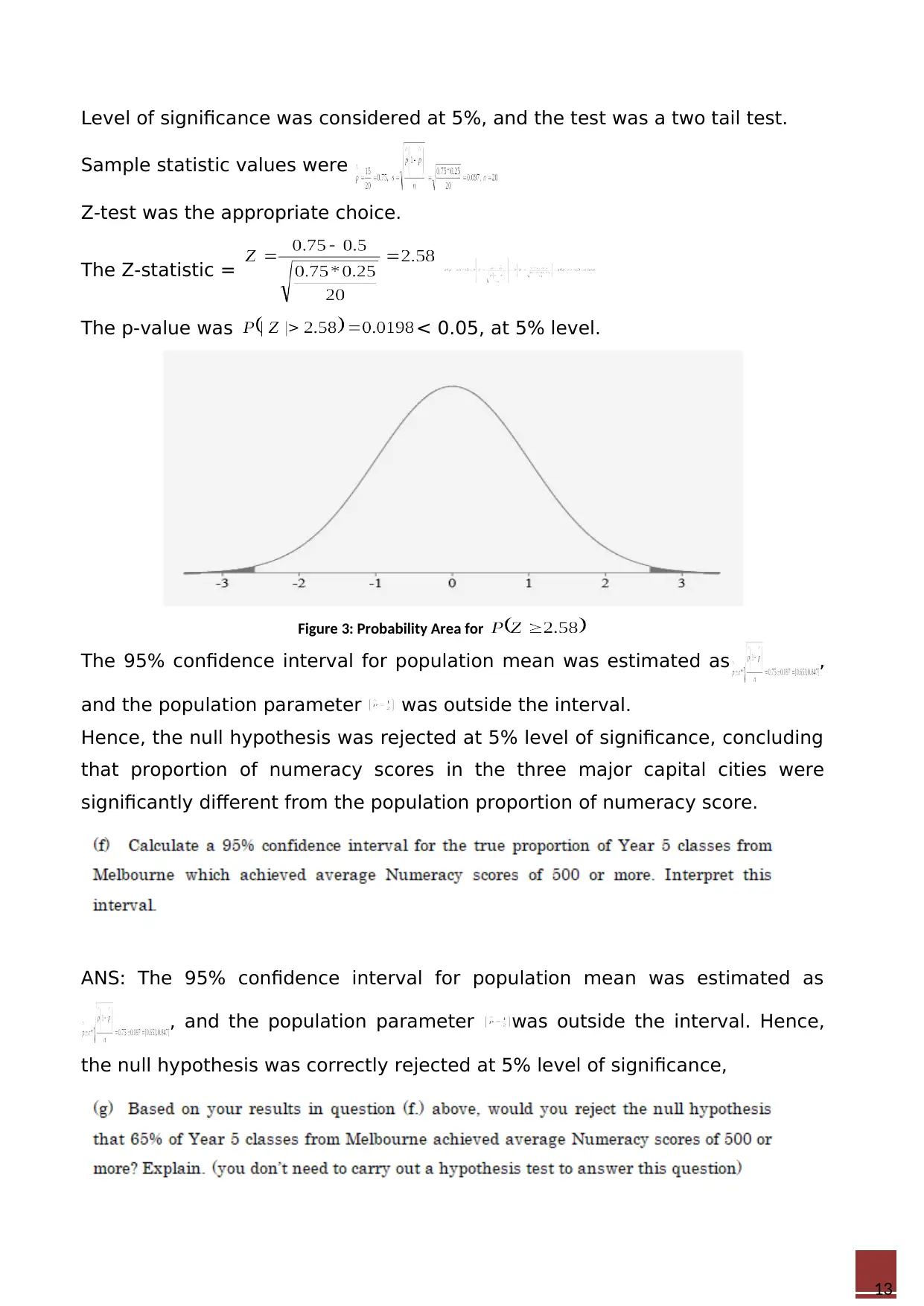
Level of significance was considered at 5%, and the test was a two tail test.
Sample statistic values were
Z-test was the appropriate choice.
The Z-statistic =
The p-value was < 0.05, at 5% level.
Figure 3: Probability Area for
The 95% confidence interval for population mean was estimated as ,
and the population parameter was outside the interval.
Hence, the null hypothesis was rejected at 5% level of significance, concluding
that proportion of numeracy scores in the three major capital cities were
significantly different from the population proportion of numeracy score.
ANS: The 95% confidence interval for population mean was estimated as
, and the population parameter was outside the interval. Hence,
the null hypothesis was correctly rejected at 5% level of significance,
Level of significance was considered at 5%, and the test was a two tail test.
Sample statistic values were
Z-test was the appropriate choice.
The Z-statistic =
The p-value was < 0.05, at 5% level.
Figure 3: Probability Area for
The 95% confidence interval for population mean was estimated as ,
and the population parameter was outside the interval.
Hence, the null hypothesis was rejected at 5% level of significance, concluding
that proportion of numeracy scores in the three major capital cities were
significantly different from the population proportion of numeracy score.
ANS: The 95% confidence interval for population mean was estimated as
, and the population parameter was outside the interval. Hence,
the null hypothesis was correctly rejected at 5% level of significance,

13
ANS: Sample statistic values were
The 95% confidence interval for population mean was estimated as ,
and the population parameter was still outside the interval. Hence, the null
hypothesis would be still rejected at 5% level of significance,
ANS: Descriptive statistics for the average Writing scores of Year 3 children
from Sydney schools and Melbourne schools in 2015 was as follows.
Table 1
Descriptive Statistics for Writing Scores for Sydney Schools and Melbourne Schools
Descriptives Writing_Sydney Writing_Melbourne
Mean 439.16 439.9
Standard Error 5.19 5.29
Median 442 444.5
Mode 438 455
Standard Deviation 22.64 23.66
Sample Variance 512.36 559.57
Kurtosis 0.46 0.12
Skewness -0.95 -0.15
Range 85 93
Minimum 384 394
Maximum 469 487
Count 19 20
ANS: Null hypothesis: H0:
Alternate Hypothesis: HA: where and were the variances of
Writing scores of Year 3 children from Sydney schools and Melbourne schools
in 2015.
Level of significance was considered at 5%, and the test was a two tail test.
ANS: Sample statistic values were
The 95% confidence interval for population mean was estimated as ,
and the population parameter was still outside the interval. Hence, the null
hypothesis would be still rejected at 5% level of significance,
ANS: Descriptive statistics for the average Writing scores of Year 3 children
from Sydney schools and Melbourne schools in 2015 was as follows.
Table 1
Descriptive Statistics for Writing Scores for Sydney Schools and Melbourne Schools
Descriptives Writing_Sydney Writing_Melbourne
Mean 439.16 439.9
Standard Error 5.19 5.29
Median 442 444.5
Mode 438 455
Standard Deviation 22.64 23.66
Sample Variance 512.36 559.57
Kurtosis 0.46 0.12
Skewness -0.95 -0.15
Range 85 93
Minimum 384 394
Maximum 469 487
Count 19 20
ANS: Null hypothesis: H0:
Alternate Hypothesis: HA: where and were the variances of
Writing scores of Year 3 children from Sydney schools and Melbourne schools
in 2015.
Level of significance was considered at 5%, and the test was a two tail test.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

13
Sample statistic values were
The F-test was the appropriate choice. The F-test was performed in Excel to
test the hypothesis at 5% level.
Table 2: F-test for Two Sample Variances
F-Test Two-Sample for Variances
Writing_Sydney Writing_Melbourne
Mean 439.16 439.90
Variance 512.36 559.57
Observations 19 20
df 18 19
F 0.92
P(F<=f) one-tail 0.428
F Critical one-tail 0.45
The F-calculated was 0.92, and p-value = 0.428 > 0.05, at 5% level.
Hence, the null hypothesis failed to get rejected at 5% level of significance,
concluding that there was no statistically significant difference in variances of
writing scores of Year 3 children from Sydney schools and Melbourne schools in
2015.
.
ANS: Null hypothesis: H0:
Alternate Hypothesis: HA:
Level of significance was considered at 5%, and the test was a two tail test.
Sample statistic values were
Due to absence of population standard deviations, t-test with equal variances
(from 2.b) was the appropriate choice.
Sample statistic values were
The F-test was the appropriate choice. The F-test was performed in Excel to
test the hypothesis at 5% level.
Table 2: F-test for Two Sample Variances
F-Test Two-Sample for Variances
Writing_Sydney Writing_Melbourne
Mean 439.16 439.90
Variance 512.36 559.57
Observations 19 20
df 18 19
F 0.92
P(F<=f) one-tail 0.428
F Critical one-tail 0.45
The F-calculated was 0.92, and p-value = 0.428 > 0.05, at 5% level.
Hence, the null hypothesis failed to get rejected at 5% level of significance,
concluding that there was no statistically significant difference in variances of
writing scores of Year 3 children from Sydney schools and Melbourne schools in
2015.
.
ANS: Null hypothesis: H0:
Alternate Hypothesis: HA:
Level of significance was considered at 5%, and the test was a two tail test.
Sample statistic values were
Due to absence of population standard deviations, t-test with equal variances
(from 2.b) was the appropriate choice.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

13
Table 3: T-test for Two Sample t-test
t-Test: Two-Sample Assuming Equal Variances
Writing_Sydney Writing_Melbourne
Mean 439.16 439.90
Variance 512.36 559.57
Observations 19 20
Pooled Variance 536.60
Hypothesized Mean Difference 0
df 37
t Stat -0.10
P(T<=t) one-tail 0.460
t Critical one-tail 1.69
P(T<=t) two-tail 0.921
t Critical two-tail 2.03
The t-statistic = with 37 degrees of freedom.
The p-value was > 0.05, at 5% level.
Hence, the null hypothesis failed to get rejected at 5% level of significance,
concluding that there was no statistically significant difference in the average
writing scores of Year 3 children from Melbourne schools and Sydney schools in
2015.
ANS: The p-value was > 0.05, for two tail test at 5% level.
Hence, the null hypothesis failed to get rejected at 5% level of significance,
concluding that there was no statistically significant difference in the average
writing scores of Year 3 children from Melbourne schools and Sydney schools in
2015.
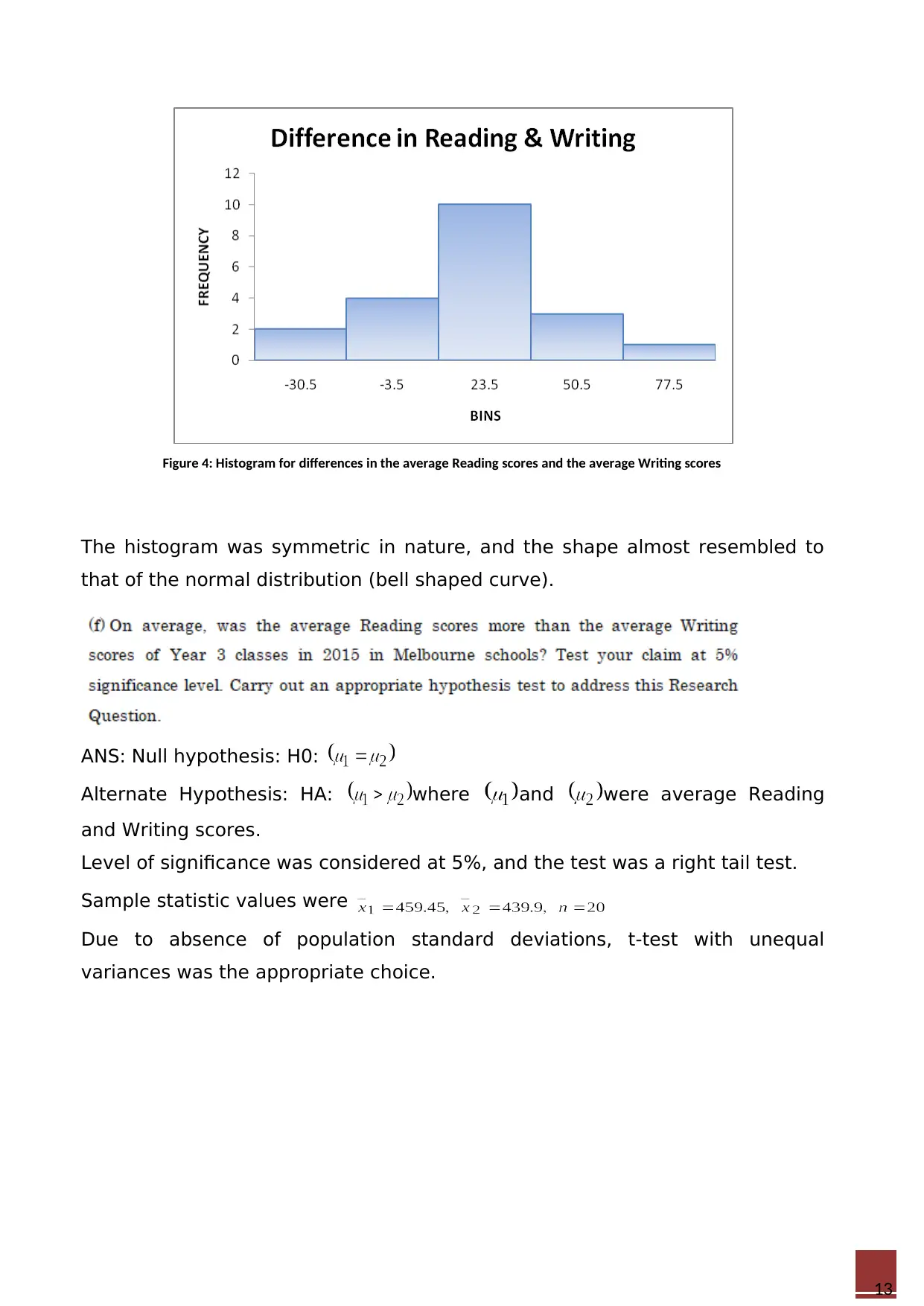
ANS: Histogram for the differences in the average Reading scores and the
average Writing scores of Year 3 classes in 2015 in Melbourne schools is as
follows.
Table 3: T-test for Two Sample t-test
t-Test: Two-Sample Assuming Equal Variances
Writing_Sydney Writing_Melbourne
Mean 439.16 439.90
Variance 512.36 559.57
Observations 19 20
Pooled Variance 536.60
Hypothesized Mean Difference 0
df 37
t Stat -0.10
P(T<=t) one-tail 0.460
t Critical one-tail 1.69
P(T<=t) two-tail 0.921
t Critical two-tail 2.03
The t-statistic = with 37 degrees of freedom.
The p-value was > 0.05, at 5% level.
Hence, the null hypothesis failed to get rejected at 5% level of significance,
concluding that there was no statistically significant difference in the average
writing scores of Year 3 children from Melbourne schools and Sydney schools in
2015.
ANS: The p-value was > 0.05, for two tail test at 5% level.
Hence, the null hypothesis failed to get rejected at 5% level of significance,
concluding that there was no statistically significant difference in the average
writing scores of Year 3 children from Melbourne schools and Sydney schools in
2015.
ANS: Histogram for the differences in the average Reading scores and the
average Writing scores of Year 3 classes in 2015 in Melbourne schools is as
follows.
13
Figure 4: Histogram for differences in the average Reading scores and the average Writing scores
The histogram was symmetric in nature, and the shape almost resembled to
that of the normal distribution (bell shaped curve).
ANS: Null hypothesis: H0:
Alternate Hypothesis: HA: where and were average Reading
and Writing scores.
Level of significance was considered at 5%, and the test was a right tail test.
Sample statistic values were
Due to absence of population standard deviations, t-test with unequal
variances was the appropriate choice.
Figure 4: Histogram for differences in the average Reading scores and the average Writing scores
The histogram was symmetric in nature, and the shape almost resembled to
that of the normal distribution (bell shaped curve).
ANS: Null hypothesis: H0:
Alternate Hypothesis: HA: where and were average Reading
and Writing scores.
Level of significance was considered at 5%, and the test was a right tail test.
Sample statistic values were
Due to absence of population standard deviations, t-test with unequal
variances was the appropriate choice.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

13
Table 4: T-test for Two Sample
t-Test: Two-Sample Assuming Unequal Variances
Reading Writing
Mean 459.45 439.9
Variance 1023.42 559.57
Observations 20 20
Hypothesized Mean Difference 0
df 35
t Stat 2.197
P(T<=t) one-tail 0.017
t Critical one-tail 1.690
P(T<=t) two-tail 0.035
t Critical two-tail 2.030
The t-statistic = 2.197 with 35 degrees of freedom.
The p-value was < 0.05, at 5% level.
Hence, the null hypothesis was rejected at 5% level of significance, concluding
that the average Reading scores were statistically significantly more than the
average writing scores of Year 3 classes (Fang, 2017).
ANS: The 95% confidence interval for average numeracy score of mean
difference in average Reading scores and average Writing scores of Year 3
classes was estimated as ,
and the difference in average Reading scores and average Writing scores was
found to be outside the interval. Hence, the null hypothesis was correctly
rejected at 5% level of significance.
Table 4: T-test for Two Sample
t-Test: Two-Sample Assuming Unequal Variances
Reading Writing
Mean 459.45 439.9
Variance 1023.42 559.57
Observations 20 20
Hypothesized Mean Difference 0
df 35
t Stat 2.197
P(T<=t) one-tail 0.017
t Critical one-tail 1.690
P(T<=t) two-tail 0.035
t Critical two-tail 2.030
The t-statistic = 2.197 with 35 degrees of freedom.
The p-value was < 0.05, at 5% level.
Hence, the null hypothesis was rejected at 5% level of significance, concluding
that the average Reading scores were statistically significantly more than the
average writing scores of Year 3 classes (Fang, 2017).
ANS: The 95% confidence interval for average numeracy score of mean
difference in average Reading scores and average Writing scores of Year 3
classes was estimated as ,
and the difference in average Reading scores and average Writing scores was
found to be outside the interval. Hence, the null hypothesis was correctly
rejected at 5% level of significance.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
13
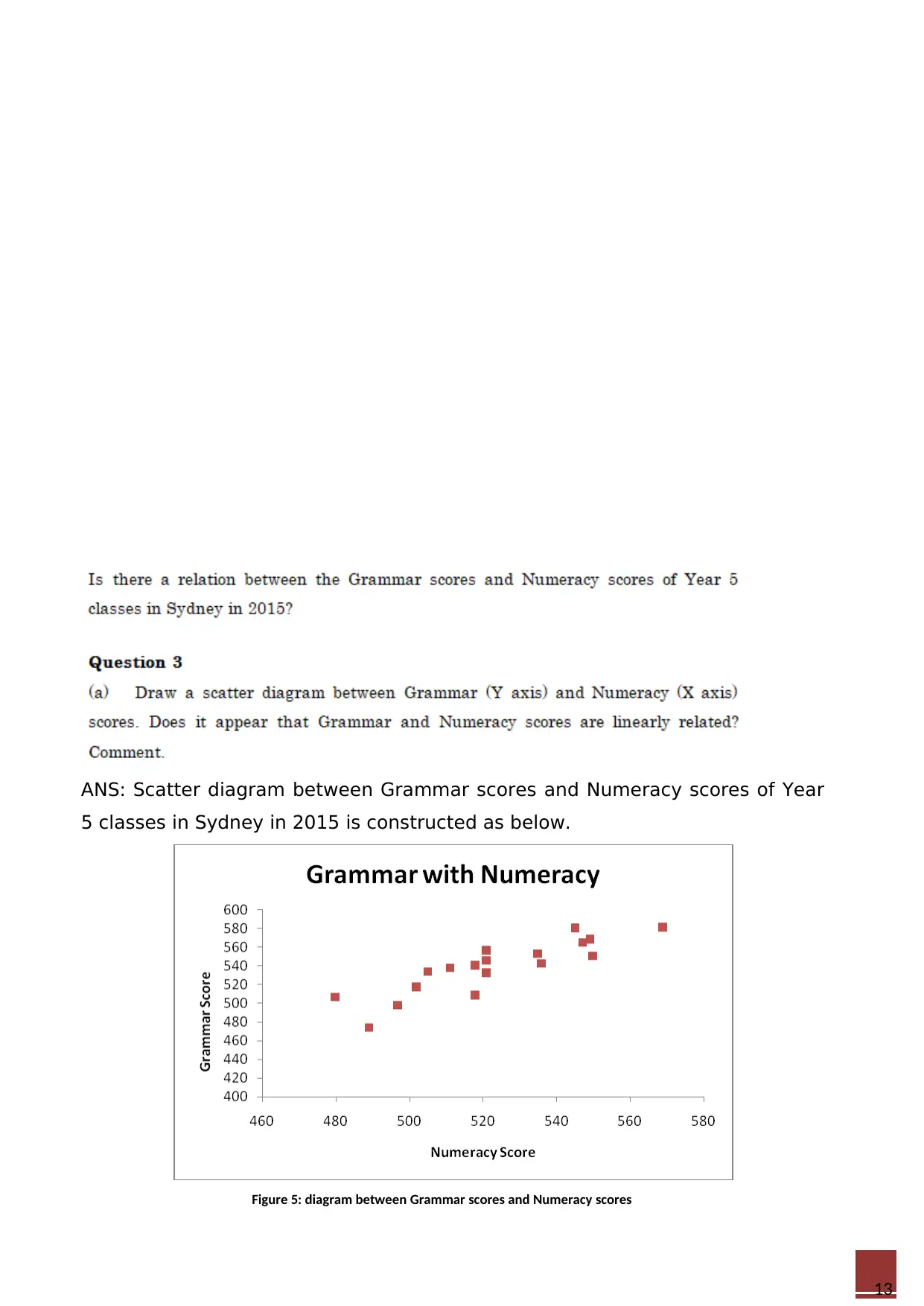
ANS: Scatter diagram between Grammar scores and Numeracy scores of Year
5 classes in Sydney in 2015 is constructed as below.
Figure 5: diagram between Grammar scores and Numeracy scores
ANS: Scatter diagram between Grammar scores and Numeracy scores of Year
5 classes in Sydney in 2015 is constructed as below.
Figure 5: diagram between Grammar scores and Numeracy scores

13
It appeared that Grammar and Numeracy scores were linearly positively
related. Grammar scores were noted to increase linearly with increase in
Numeracy scores.
ANS: Excel was used to estimate the regression line of Grammar on Numeracy
scores. The estimated regression line was ,
where was the residual of the estimated equation
Table 5: regression Model of Grammar on Numeracy scores
Regression Statistics
Multiple R 0.885
R Square 0.782
Adjusted R Square 0.770
Standard Error 14.264
Observations 19
ANOVA
df SS MS F Significance F
Regression 1 12443.02203 12443.02203 61.152 0.000
Residual 17 3459.083231 203.475
Total 18 15902.10526
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept -4.656 69.813 -0.067 0.948 -151.949 142.637
Numeracy 1.038 0.133 7.820 0.000 0.758 1.318
ANS: The estimated regression line was ,
where was the residual of the estimated equation
The standard error for intercept was SE = 69.813, and that of the Numeracy
scores was SE = 0.133.
The intercept (t = -0.067, p = 0.948) was statistically insignificant, as negative
Grammar score due to zero in Numeracy scores does not make any statistical
sense.
Numeracy was statistically significant (t = 7.82, p < 0.05) predictor of
Grammar scores at 5% level of significance.
It appeared that Grammar and Numeracy scores were linearly positively
related. Grammar scores were noted to increase linearly with increase in
Numeracy scores.
ANS: Excel was used to estimate the regression line of Grammar on Numeracy
scores. The estimated regression line was ,
where was the residual of the estimated equation
Table 5: regression Model of Grammar on Numeracy scores
Regression Statistics
Multiple R 0.885
R Square 0.782
Adjusted R Square 0.770
Standard Error 14.264
Observations 19
ANOVA
df SS MS F Significance F
Regression 1 12443.02203 12443.02203 61.152 0.000
Residual 17 3459.083231 203.475
Total 18 15902.10526
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept -4.656 69.813 -0.067 0.948 -151.949 142.637
Numeracy 1.038 0.133 7.820 0.000 0.758 1.318
ANS: The estimated regression line was ,
where was the residual of the estimated equation
The standard error for intercept was SE = 69.813, and that of the Numeracy
scores was SE = 0.133.
The intercept (t = -0.067, p = 0.948) was statistically insignificant, as negative
Grammar score due to zero in Numeracy scores does not make any statistical
sense.
Numeracy was statistically significant (t = 7.82, p < 0.05) predictor of
Grammar scores at 5% level of significance.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

13
The sample size was 19, and the coefficient of determination (R-square) =
0.782. Hence, Numeracy was able to explain 78.2% variation in Grammar
scores.
ANS: The slope coefficient was 1.038, which signified a significant strong
positive linear relation between the two variables. The angle of the regression
line was noted to be greater than 45 degrees, as the slope was greater than 1.
ANS: Null hypothesis: H0: (No linear relation exists)
Alternate Hypothesis: HA:
Level of significance was considered at 5%, and the test was a two tail test.
Sample statistic values were
Due to absence of population standard deviation, t-test was the appropriate
choice.
The t-statistic = with 18 degrees of freedom.
The p-value was < 0.05, at 5% level.
The 95% confidence interval for population mean was estimated as
, and the population parameter
was outside the interval.
Hence, the null hypothesis was rejected at 5% level of significance, concluding
that a statistically significant linear relation exists between Grammar scores
and Numeracy scores of Year 5 classes in Sydney in 2015 (Chatterjee, & Hadi,
2015).
References
The sample size was 19, and the coefficient of determination (R-square) =
0.782. Hence, Numeracy was able to explain 78.2% variation in Grammar
scores.
ANS: The slope coefficient was 1.038, which signified a significant strong
positive linear relation between the two variables. The angle of the regression
line was noted to be greater than 45 degrees, as the slope was greater than 1.
ANS: Null hypothesis: H0: (No linear relation exists)
Alternate Hypothesis: HA:
Level of significance was considered at 5%, and the test was a two tail test.
Sample statistic values were
Due to absence of population standard deviation, t-test was the appropriate
choice.
The t-statistic = with 18 degrees of freedom.
The p-value was < 0.05, at 5% level.
The 95% confidence interval for population mean was estimated as
, and the population parameter
was outside the interval.
Hence, the null hypothesis was rejected at 5% level of significance, concluding
that a statistically significant linear relation exists between Grammar scores
and Numeracy scores of Year 5 classes in Sydney in 2015 (Chatterjee, & Hadi,
2015).
References
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

13
Chatterjee, S., & Hadi, A. S. (2015). Regression analysis by example. John
Wiley & Sons.
Fang, K. W. (2017). Symmetric Multivariate and Related Distributions: 0.
Chapman and Hall/CRC.
Chatterjee, S., & Hadi, A. S. (2015). Regression analysis by example. John
Wiley & Sons.
Fang, K. W. (2017). Symmetric Multivariate and Related Distributions: 0.
Chapman and Hall/CRC.
1 out of 14
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.




