Econometrics Assignment: Regression Analysis and Statistical Inference

This econometrics assignment presents three distinct problems. The first involves predicting bear weight using linear and logarithmic regression models, analyzing variables like head length, neck circumference, and chest circumference, and applying backward elimination to refine the models. Th...Read More

Running head: ECONOMETRICS
ECONOMETRICS
Name of the Student
Name of the University
Author Note

1ECONOMETRICS
Assignment 1:
In this assignment all the variables from the ‘bears.xls’ files are first extracted and then a
prediction model(regression) for bear weight is performed with respect to other variables
chosen as independent variables. The variables are listed as follows.
MonthObs: The month in which each of bears are measured.
Gender: The gender of bears, 1 = male and 2 =female
HeadLengthInches: Head length of the bears measured in inches.
NeckInches: Circumference of the neck of bears measured in inches.
BodyLengthInches: length of the body of bears measured in inches.
ChestInches: circumference of the chest of bears measured in inches.
WeightPounds: Weight of the bears measured in pounds.
The sample of 54 bears is collected by the scientist assumed are collected in random
sampling method. From the sample the regression is performed to measure the weight of the
bears as it is practically very much difficult or impossible to measure the weight of the bears
individually. The linear regression model is performed in MATLAB which is shown below.
All the units are converted to metric form (weight of bears in Kgs and lengths or
circumference in meters).
MATLAB code:
bears = readtable('bears.xls','ReadVariableNames',true);
Meter = 1*0.0254; % inch to meter conversion unit
KGs = 1*0.45359227; % pounds to Kg conversion unit

2ECONOMETRICS
HeadLengthM = bears.HeadLengthInches.*Meter;
HeadWidthM = bears.HeadWidthInches.*Meter;
NeckM = bears.NeckInches.*Meter;
BodyLengthM = bears.BodyLengthInches.*Meter;
ChestM = bears.ChestInches.*Meter;
WeightKG = bears.WeightPounds.*KGs;
Regression = fitlm([HeadLengthM HeadWidthM NeckM BodyLengthM
ChestM],WeightKG) % Regression with linear variables
LogHeadLengthM = log(HeadLengthM);
LogHeadWidthM = log(HeadWidthM);
LogNeckM = log(NeckM);
LogBodyLengthM = log(BodyLengthM);
LogChestM = log(ChestM);
LogWeightKG = log(WeightKG);
LogRegression = fitlm([LogHeadLengthM LogHeadWidthM LogNeckM
LogBodyLengthM LogChestM],LogWeightKG) % Fitting Regression with logarithmic
variables
Output:
assign1
Regression =

3ECONOMETRICS
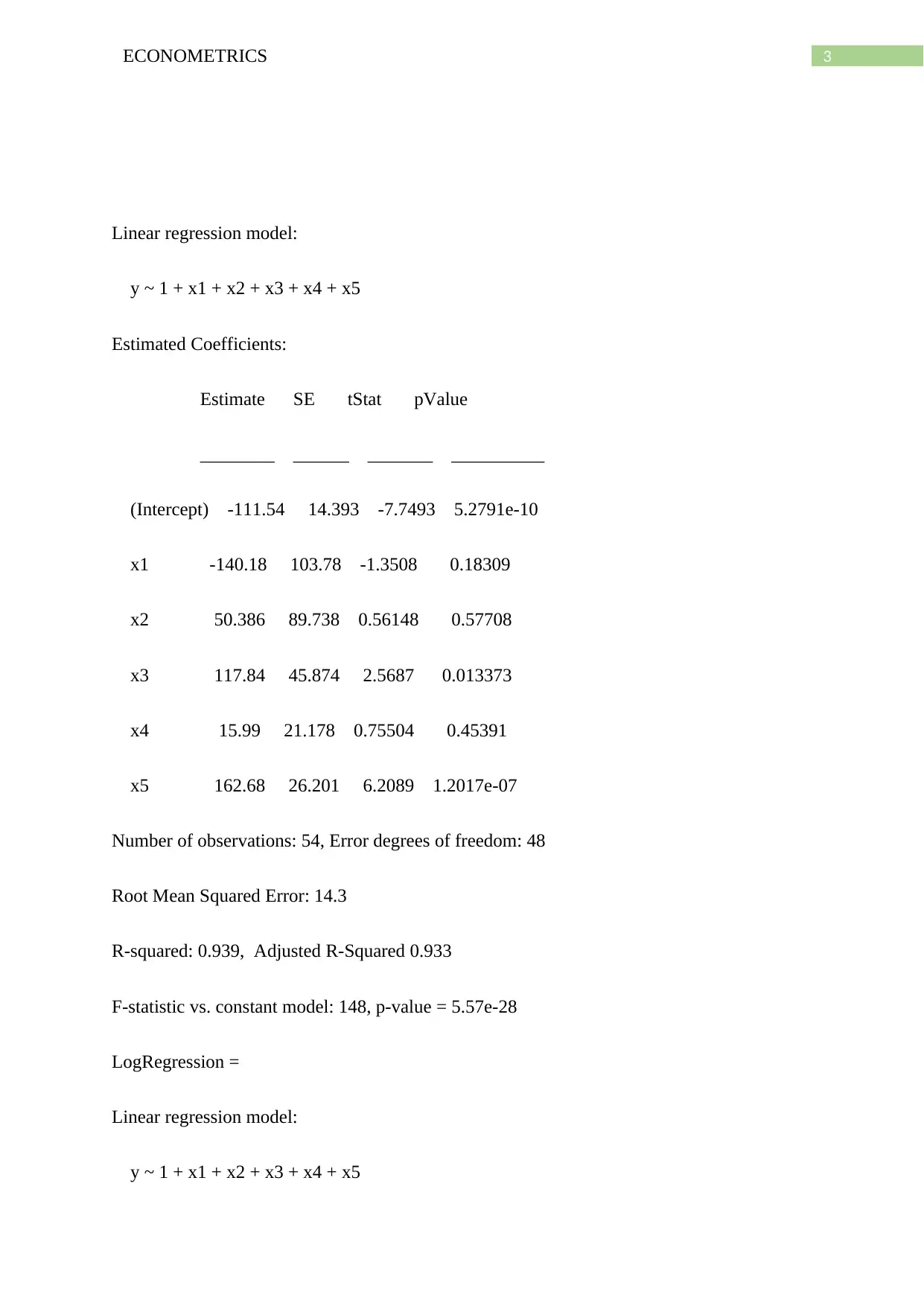
Linear regression model:
y ~ 1 + x1 + x2 + x3 + x4 + x5
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ _______ __________
(Intercept) -111.54 14.393 -7.7493 5.2791e-10
x1 -140.18 103.78 -1.3508 0.18309
x2 50.386 89.738 0.56148 0.57708
x3 117.84 45.874 2.5687 0.013373
x4 15.99 21.178 0.75504 0.45391
x5 162.68 26.201 6.2089 1.2017e-07
Number of observations: 54, Error degrees of freedom: 48
Root Mean Squared Error: 14.3
R-squared: 0.939, Adjusted R-Squared 0.933
F-statistic vs. constant model: 148, p-value = 5.57e-28
LogRegression =
Linear regression model:
y ~ 1 + x1 + x2 + x3 + x4 + x5

4ECONOMETRICS
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ ________ __________
(Intercept) 4.4229 0.42166 10.489 5.1817e-14
x1 -0.10279 0.29287 -0.35096 0.72715
x2 0.13452 0.12769 1.0535 0.29739
x3 0.49422 0.16147 3.0607 0.0036101
x4 1.1175 0.26719 4.1825 0.00012176
x5 1.4531 0.19754 7.3559 2.0979e-09
Number of observations: 54, Error degrees of freedom: 48
Root Mean Squared Error: 0.121
R-squared: 0.976, Adjusted R-Squared 0.974
F-statistic vs. constant model: 391, p-value = 1.19e-37
Here, y is bear weight in linear model and logarithmic model respectively and x1, x2…x5 are
the predictor variables as specified in the corresponding linear and logarithmic model.
Hence, the linear regression model is fitted with the sample for the variables in linear scale.
As it can be seen that the adjusted R2 value for the model is 0.933 or the variables can explain
93.30% of variation in the bear weight in kilograms. The regression model is
WeigthKG = -111.54 -140.18*HeadLengthM + 50.386*HeadWidthM + 117.84* NeckM +
15.99*BodyLengthM + 162.68*ChestM.
Similarly, the logarithmic regression model is

5ECONOMETRICS
LogWeightKG = 4.4229 + -0.10279*LogHeadLengthM + 0.13452*LogHeadWidthM +
0.49422*LogNeckM + 1.1175*LogBodyLengthM + 1.4531*LogChestM.
The model has the adjusted R^2 value of 0.974 (97.4% of variation is explained by the
model) and overall p value of 1.19e-37.
Now, backward elimination method is applied to find the most suitable models in the both
logarithmic and linear model. In this method the considered significance level is 0.05. Hence,
in each step the predictor coefficient with highest p value is removed until all the coefficients
have the p values less than 0.05. The final regression model is given below.
Regression =
Linear regression model:
y ~ 1 + x3 + x5
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ _______ __________
(Intercept) -121.14 7.6844 -15.764 3.0186e-21
x3 103.05 38.267 2.693 0.0095594
x5 165.91 23.082 7.1879 2.7478e-09
Number of observations: 54, Error degrees of freedom: 51
Root Mean Squared Error: 14.2
R-squared: 0.937, Adjusted R-Squared 0.934
F-statistic vs. constant model: 377, p-value = 2.78e-31

6ECONOMETRICS
LogRegression =
Linear regression model:
LogWeightKG ~ 1 + LogNeckM + LogBodyLengthM + LogChestM
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ ______ __________
(Intercept) 4.3374 0.13073 33.177 1.022e-35
x3 0.53435 0.14416 3.7067 0.00052609
x4 1.0668 0.20007 5.3322 2.3376e-06
x5 1.4864 0.1933 7.6895 5.0396e-10
Number of observations: 54, Error degrees of freedom: 50
Root Mean Squared Error: 0.12
R-squared: 0.975, Adjusted R-Squared 0.974
F-statistic vs. constant model: 662, p-value = 3.22e-40
Hence, the final linear regression model which predicts the bear weight is
WeightKG = -121.14 + 103.05*NeckM + 165.91*ChestM.
The R^2 value is 93.4% which has not changed and p value has been decreased. Hence, this
model expresses bear weight with the most significant number of coefficients.
The final logarithmic regression model is given below.

7ECONOMETRICS
LogWeightKG = 4.3374 + 0.53435*LogNeckM + 1.0668*LogBodyLengthM +
1.4864*LogChestM.
This explains 97.4% of log of bear weight with the p value of 3.22e-40.
Assignment 2:
A) In this assignment the variables are first extracted from the beauty.xls file is extracted
as given below. A total of 1260 people has been sampled.
1. wage hourly wage
2. lwage log(wage)
3. belavg =1 if looks <= 2
4. abvavg =1 if looks >=4
5. exper years of workforce experience
6. looks from 1 to 5
7. union =1 if union member
8. goodhlth =1 if good health
9. black =1 if black
10. female =1 if female
11. married =1 if married
12. south =1 if live in south
13. bigcity =1 if live in big city
14. smllcity =1 if live in small city
15. service =1 if service industry
16. educ years of schooling
I. The number of men who have more than 10 years of experience and do not live in the
big city is determined from the following MATLAB code.

8ECONOMETRICS
MATLAB code:
%(A)
beauty = readtable('beauty.xls','ReadVariableNames',true);
beauty.Properties.VariableNames = {'wage' 'lwage' 'belavg' 'abvavg' 'exper' 'looks'
'union' 'goodhlth' 'black' 'female' 'married' 'south' 'bigcity' 'smllcity' 'service' 'educ'};
%(I)
men_more10_smallcity = beauty.female == 0 & beauty.exper >= 10 &
beauty.bigcity == 0;
num_men_more10_smllcity = sum(men_more10_smallcity)
Output:
num_men_more10_smllcity =
487
Hence, 487 men are more than 10 years of experience and do not live in big city or
live in small city.
II. The married men who are good health and who live in big city are calculated by the
following code.
MATLAB code:
beauty = readtable('beauty.xls','ReadVariableNames',true);
beauty.Properties.VariableNames = {'wage' 'lwage' 'belavg' 'abvavg' 'exper' 'looks'
'union' 'goodhlth' 'black' 'female' 'married' 'south' 'bigcity' 'smllcity' 'service' 'educ'};
%(II)
menmarriedandgood = beauty.female == 0 & beauty.married == 1 &
beauty.goodhlth==1 & beauty.bigcity == 1;
nummenmarriedandgood = sum(menmarriedandgood)
Output:

9ECONOMETRICS
nummenmarriedandgood =
133
Hence, there are 133 men who are in good health and live in big city.
B)
I) Now, the linear regression model of log(wage) is fitted with MATLAB in this
part.
The natural log of hourly wage is fitted by regression line with respect to the other
independent variables as given below.
The regression model is given by,
lwage = β0 + β1*exper + β2*exper^2 + β3*educ + μ
Hence, the MATLAB function of fitlm for implementing this model will be
fitlm(beauty,'lwage ~ exper + exper^2 + educ')
Now, when the coefficients β1 and β2 are non-linear function of educ then the
modified regression will be of the form
lwage = β0 + (α0 + α1*educ)*exper + (α2 + α3)*exper^2 + β3*educ + μ
Hence, the MATLAB function of fitlm for implementing the model will be
fitlm(beauty,'lwage ~ exper + educ*exper + exper^2 + educ*exper^2 + educ')
Now, the coefficient test of the regression coefficients can be obtained by the coefTest
function in MATLAB, This determines the p value of the coefficient.
MATLAB code:
beauty = readtable('beauty.xls','ReadVariableNames',true);
beauty.Properties.VariableNames = {'wage' 'lwage' 'belavg' 'abvavg' 'exper' 'looks'
'union' 'goodhlth' 'black' 'female' 'married' 'south' 'bigcity' 'smllcity' 'service' 'educ'};
%(B)
beauty.educXexper = (beauty.educ.*beauty.exper);

10ECONOMETRICS
beauty.eeduc = (beauty.educ);
beauty.educXexper2 = (beauty.educ.*beauty.exper.^2);
normalREG = fitlm(beauty,'lwage ~ exper + exper^2 + educ')
modifiedRegression = fitlm(beauty,'lwage ~ exper + educ*exper + exper^2 +
educ*exper^2 + educ')
CoeficientTestexpsqr = coefTest(modifiedRegression,[0 0 0 1 0 0])
CoeficientTesteduc = coefTest(modifiedRegression,[0 0 0 0 0 1])
CoeficientTestexpsqrandeduc = coefTest(modifiedRegression,[0 0 0 1 0 1])
Output:
normalREG =
Linear regression model:
lwage ~ 1 + exper + educ + exper^2
Estimated Coefficients:
Estimate SE tStat pValue
___________ __________ _______ __________
(Intercept) 0.22669 0.08384 2.7039 0.006946
exper 0.047972 0.0047955 10.004 1.0152e-22
educ 0.070588 0.0057811 12.21 1.7578e-32
exper^2 -0.00069106 0.00010797 -6.4004 2.1842e-10
Number of observations: 1259, Error degrees of freedom: 1255
Root Mean Squared Error: 0.523
R-squared: 0.228, Adjusted R-Squared 0.226
F-statistic vs. constant model: 123, p-value = 6.03e-70
modifiedRegression =

11ECONOMETRICS
Linear regression model:
lwage ~ 1 + exper*educ + exper^2 + (exper^2):educ
Estimated Coefficients:
Estimate SE tStat pValue
___________ __________ _______ ________
(Intercept) 0.53352 0.24651 2.1643 0.03063
exper 0.0081129 0.02438 0.33276 0.73937
educ 0.045287 0.019566 2.3146 0.020798
exper:educ 0.0033031 0.0019588 1.6863 0.091981
exper^2 0.0002062 0.00050714 0.40658 0.68438
exper^2:educ -7.5159e-05 4.1263e-05 -1.8214 0.068777
Number of observations: 1259, Error degrees of freedom: 1253
Root Mean Squared Error: 0.523
R-squared: 0.23, Adjusted R-Squared 0.227
F-statistic vs. constant model: 74.7, p-value = 1.36e-68
CoeficientTestexpsqr =
0.0920
CoeficientTesteduc =
0.0688
CoeficientTestexpsqrandeduc =
0.0928
II) Hence, the modified regression model is

12ECONOMETRICS
lwage = 0.53352 + 0.0008* exper + 0.045*educ + 0.0033*exper*educ + 0.0002*
exper^2 -7.515e(-5)* (exper^2*educ).
This model has low adjusted R^2 = 0.227 or only 22.7% variability in log of wage
is explained by the predictor variables.
From the coefficient test it is found that the p value of exper^2 (square of years of
workforce experience) is 0.092, the p value of educ (years of schooling) is 0.0688
and p value of the interaction exper^2*educ is 0.0928. Hence, assuming a
significance of 0.05 it can be concluded that none of the three coefficients is
significant.
C) In the table 2 of the Kanazawa paper the correlation matrix between the variables
from IQ to Age at puberty along with mean and standard deviation of men and
women are given. The p values of each coefficient is presented using stars next to the
correlation. The 3 p values that are used in the paper is 0.05, 0.01 and 0.001
respectively. Now, in the full regression model of log (wage) the correlations between
individual coefficients are not represented but the overall correlation is presented with
overall p value. However, the exact p values of each coefficients is presented by the
regression table. Hence, the regression table can be used form the regression model
along with significant coefficients from the p value but correlations between them is
unknown. Whereas, the correlation matrix gives the correlations between the variable
along with their central measures but predictive model can’t be formed from it.
Assignment 3:
A) In this part two sets of Independent and identically distributed random variables of
length n= 5000 (X1,X2….Xn and Y1,Y2,….Yn) are generated from the standard
normal distribution. Then from those variables a new set of two variables Xmod and

13ECONOMETRICS
Ymod are formed in such a way that {Xi,Yi} is inside (-∞,-1) U (1,∞). A scatter plot
of Ymod vs Xmod is also presented.
MATLAB code:
rng(650)
n = 5000;
miu = 0;
sigma = 1;
X = normrnd(miu, sigma, n, 1);
Y = normrnd(miu, sigma, n, 1);
Condition = abs(X) > 1 & abs(Y) > 1;
Xmod = nonzeros(X.*Condition);
Ymod = nonzeros(Y.*Condition);
corrXmodYmod = corr(Xmod,Ymod)
scatter(Xmod,Ymod,'ro')
xlabel('Xmod')
ylabel('Ymod')
title('Scatter Plot, Xmod Ymod')
corrXmodYmod =
0.0396
Output:
corrXmodYmod =
0.0396

14ECONOMETRICS
-4 -3 -2 -1 0 1 2 3 4
Xmod
-4
-3
-2
-1
0
1
2
3
4
Ymod
Scatter Plot, Xmod Ymod
The correlation coefficient is close to zero and hence it shows that the random
variables are independent.
B) The simulated sample gives the result of the probability
I) P(X1 ∈ (-∞,-1) U (1,∞), Y1 ∈ (-∞,-1) U (1,∞)) = sum of the pairs of
(Xi,Yi) which lies in the region / 5000 = 0.0972.
MATLAB code:
Probability = sum(Condition)/n;
Probability =
0.0972
II)
The empirical covariance and the empirical correlation between X and Y are very
close as the Correlation (R) = Cov(X,Y)/(Sx*Sy). Hence, the if covariance is low then

15ECONOMETRICS
correlation will also be low and vice versa. In MATLAB covariance matrix and
correlation is calculated.
MATLAB code:
corr(X,Y)
ans =
0.0233
cov(X,Y)
ans =
0.9996 0.0233
0.0233 1.0019
III)
Now, the average of X1,X2,…Xn is very close to the average of Xmod because
only the Xi values in the range [-1,1] is removed in Xmod. Now, the values are
generated from standard normal distribution hence the mean will be close to zero.
Now, in case of Xmod which is formed after removing the values in the range [-
1,1] from X1,X2,…Xn keeps the distribution symmetric. Hence, the mean is very
close to zero for Xmod. Two histograms with line pointing the mean are drawn in
MATLAB to show this concept.
MATLAB program:
subplot(2,1,1)
histogram(X)
ylim([0,500])
xlim([-4,4])
yL = get(gca,'YLim');
line([mean(X) mean(X)],yL,'Color','r');

16ECONOMETRICS
xlabel('X')
ylabel('Density')
title('Histogram for X')
mean(X);
subplot(2,1,2);
histogram(Xmod);
ylim([0,500])
xlim([-4,4])
yL = get(gca,'YLim');
line([mean(Xmod) mean(Xmod)],yL,'Color','r');
xlabel('Xmod')
ylabel('Density')
title('Histogram for Xmod')
mean(Xmod)
Plot:

17ECONOMETRICS
Histogram for X
-4 -3 -2 -1 0 1 2 3 4
X
0
100
200
300
400
500
Density
Histogram for Xmod
-4 -3 -2 -1 0 1 2 3 4
Xmod
0
100
200
300
400
500
Density
C) Now, the correlations between each point of Xi and Yi (i= 1,2,…n) is calculated in
MATLAB and then the correlation vector (rn) is plotted against the different
simulated samples of size n = 100,500,1000,10^4,10^6 and 10^7. In the y axis the
correlation vector is plotted against log(n) in the x axis. The random number
generation seed (rng = 650) is used for (Xi,Yi) generation which is as same as in part
A.
MATLAB code:
miu = 0;
sigma = 1;
counter = 0;
CorrXmodYmod = zeros(1,1);
for n = [ 100 500 1000 10^4 10^6 10^7 ]
rng(6039)

18ECONOMETRICS
X = normrnd(miu, sigma, n, 1);
Y = normrnd(miu, sigma, n, 1);
Condition = abs(X) > 1 & abs(Y) > 1;
Xmod = nonzeros(X.*Condition);
Ymod = nonzeros(Y.*Condition);
counter = counter + 1;
corrXmodYmod(1, counter) = corr(Xmod,Ymod);
end
Logn = log([ 100 500 1000 10^4 10^6 10^7 ]);
plot(Logn,corrXmodYmod,'b-s','LineWidth',2)
ylim([-1,1])
xL = xlim;
line(xL, [0 0,],xL,'Color','r');
xlabel('Log (n)')
ylabel('r_n')
title('Correlations: rng(605)')
Plot:

19ECONOMETRICS
4 6 8 10 12 14 16 18
Log (n)
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
rn
Correlations: rng(650)
D) Now, the same procedure is followed as in part C but each time of (Xi,Yi) generation
a different random number seed (rng) is used. In this case rng used are 5047,5048 and
5049. It can be seen that the starting of the plot only differs but as n increases the
plots become identical. This is because with different random number seed different
numbers from standard normal distribution is produced. But, as the number of points
increases the distribution approaches towards normal distribution. Hence, with any
random number seed if the n is high enough the overall distribution will be
approximately normal. Hence, with large n the plots becomes identical. The 3 plots
with 3 random number seeds is given with MATLAB code.
MATLAB code:
miu = 0;
sigma = 1;
counter = 0;

20ECONOMETRICS
CorrXmodYmod = zeros(1,1);
for n = [ 100 500 1000 10^4 10^6 10^7 ]
rng(5047)
X = normrnd(miu, sigma, n, 1);
Y = normrnd(miu, sigma, n, 1);
Condition = abs(X) > 1 & abs(Y) > 1;
Xmod = nonzeros(X.*Condition);
Ymod = nonzeros(Y.*Condition);
counter = counter + 1;
corrXmodYmod(1, counter) = corr(Xmod,Ymod);
end
Logn = log([ 100 500 1000 10^4 10^6 10^7 ]);
p1 = subplot(2,2,1);
plot(Logn,corrXmodYmod,'b-s','LineWidth',2)
ylim([-1,1])
xL = xlim;
line(xL, [0 0,],xL,'Color','r');
xlabel('Log (n)')
ylabel('r_n')
title('Correlations: rng(5047)')

21ECONOMETRICS
%rng(5048)
miu = 0;
sigma = 1;
counter = 0;
CorrXmodYmod = zeros(1,1);
for n = [ 100 500 1000 10^4 10^6 10^7 ]
rng(5048)
X = normrnd(miu, sigma, n, 1);
Y = normrnd(miu, sigma, n, 1);
Condition = abs(X) > 1 & abs(Y) > 1;
Xmod = nonzeros(X.*Condition);
Ymod = nonzeros(Y.*Condition);
counter = counter + 1;
corrXmodYmod(1, counter) = corr(Xmod,Ymod);
end
Logn = log([ 100 500 1000 10^4 10^6 10^7 ]);
p2 = subplot(2,2,2);
plot(Logn,corrXmodYmod,'b-s','LineWidth',2)

22ECONOMETRICS
ylim([-1,1])
xL = xlim;
line(xL, [0 0,],xL,'Color','r');
xlabel('Log (n)')
ylabel('r_n')
title('Correlations: rng(5048)')
%rng(5049)
miu = 0;
sigma = 1;
counter = 0;
CorrXmodYmod = zeros(1,1);
for n = [ 100 500 1000 10^4 10^6 10^7 ]
rng(5049)
X = normrnd(miu, sigma, n, 1);
Y = normrnd(miu, sigma, n, 1);
Condition = abs(X) > 1 & abs(Y) > 1;
Xmod = nonzeros(X.*Condition);
Ymod = nonzeros(Y.*Condition);
counter = counter + 1;
corrXmodYmod(1, counter) = corr(Xmod,Ymod);
end

23ECONOMETRICS
Logn = log([ 100 500 1000 10^4 10^6 10^7 ]);
p3 = subplot(2,2,3);
plot(Logn,corrXmodYmod,'b-s','LineWidth',2)
ylim([-1,1])
xL = xlim;
line(xL, [0 0,],xL,'Color','r');
xlabel('Log (n)')
ylabel('r_n')
title('Correlations: rng(5049)')
Plot:
5 10 15
Log (n)
-1
-0.5
0
0.5
1
rn
Correlations: rng(5047)
5 10 15
Log (n)
-1
-0.5
0
0.5
1
rn
Correlations: rng(5048)
5 10 15
Log (n)
-1
-0.5
0
0.5
1
rn
Correlations: rng(5049)

24ECONOMETRICS
E) Now, the same procedure in part A is followed but with a different method. In this
case two plots are produced in which Xmod and Ymod have highly positive and
negative correlations between them respectively. At first X vector is formed by X =
x*y by this expression and Y vector is formed by Y = y*x by the expression. Then a
condition is used which returns a logical array based on whether (Xi,Yi) is in the
region {(-∞,-1) U (1,∞)}. Hence, Xmod and Ymod will result in positive correlation
as with increase in Xmod results increase in Ymod. Similarly, by expression X = x*y
and Y = y*-x will result in negative correlation as with increase in Xmod, Ymod will
be decreased.
MATLAB code:
rng(650)
n = 5000;
miu = 0;
sigma = 1;
x = normrnd(miu, sigma, n, 1);
y = normrnd(miu, sigma, n, 1);
X = x.*y;
Y = y.*x;
Condition = abs(X) > 1 & abs(Y) > 1;
Xmod = nonzeros(X.*Condition);

25ECONOMETRICS
Ymod = nonzeros(Y.*Condition);
corrXmodYmod = corr(Xmod,Ymod);
k1 = subplot(1,2,1);
scatter(Xmod,Ymod,'ro');
xlabel('Xmod');
ylabel('Ymod');
title('Scatter Plot, Xmod Ymod for highly poisitive correlation');
rng(650)
n = 5000;
miu = 0;
sigma = 1;
x = normrnd(miu, sigma, n, 1);
y = normrnd(miu, sigma, n, 1);
X = x.*y;
Y = y.*-x;
Condition = abs(X) > 1 & abs(Y) > 1;

26ECONOMETRICS
Xmod = nonzeros(X.*Condition);
Ymod = nonzeros(Y.*Condition);
corrXmodYmod = corr(Xmod,Ymod)
k1 = subplot(1,2,2);
scatter(Xmod,Ymod,'ro');
xlabel('Xmod');
ylabel('Ymod');
title('Scatter Plot, Xmod Ymod for highly negative correlation')
Output:
corrXmodYmod =
1
corrXmodYmod =
-1
-8 -6 -4 -2 0 2 4 6
Xmod
-8
-6
-4
-2
0
2
4
6
Ymod
Scatter Plot, Xmod Ymod for highly poisitive correlation
-8 -6 -4 -2 0 2 4 6
Xmod
-6
-4
-2
0
2
4
6
8
Ymod
Scatter Plot, Xmod Ymod for highly negative correlation

27ECONOMETRICS