Econometrics: Comprehensive Analysis of Linear Regression Techniques
VerifiedAdded on 2022/02/17
|22
|4508
|19
Report
AI Summary
This report provides a comprehensive overview of linear regression within the field of econometrics. It begins by defining regression and its purpose, then explores various data types including cross-sectional, time series, and panel data. Key statistical concepts such as arithmetic mean, variance, covariance, and the coefficient of linear correlation are introduced. The core of the report focuses on simple linear regression, detailing its purposes, the model, and the estimation of parameters using Ordinary Least Squares (OLS). The report explains descriptive analysis and the OLS method, along with the properties of least-square estimators. Furthermore, it connects regression analysis with the analysis of variance and discusses the coefficient of determination, R-squared, and adjusted R-squared. Finally, the report touches upon confidence intervals and significance tests for regression parameters, offering a thorough introduction to linear regression techniques and applications in econometrics.
Chapter 1
Linear Regression
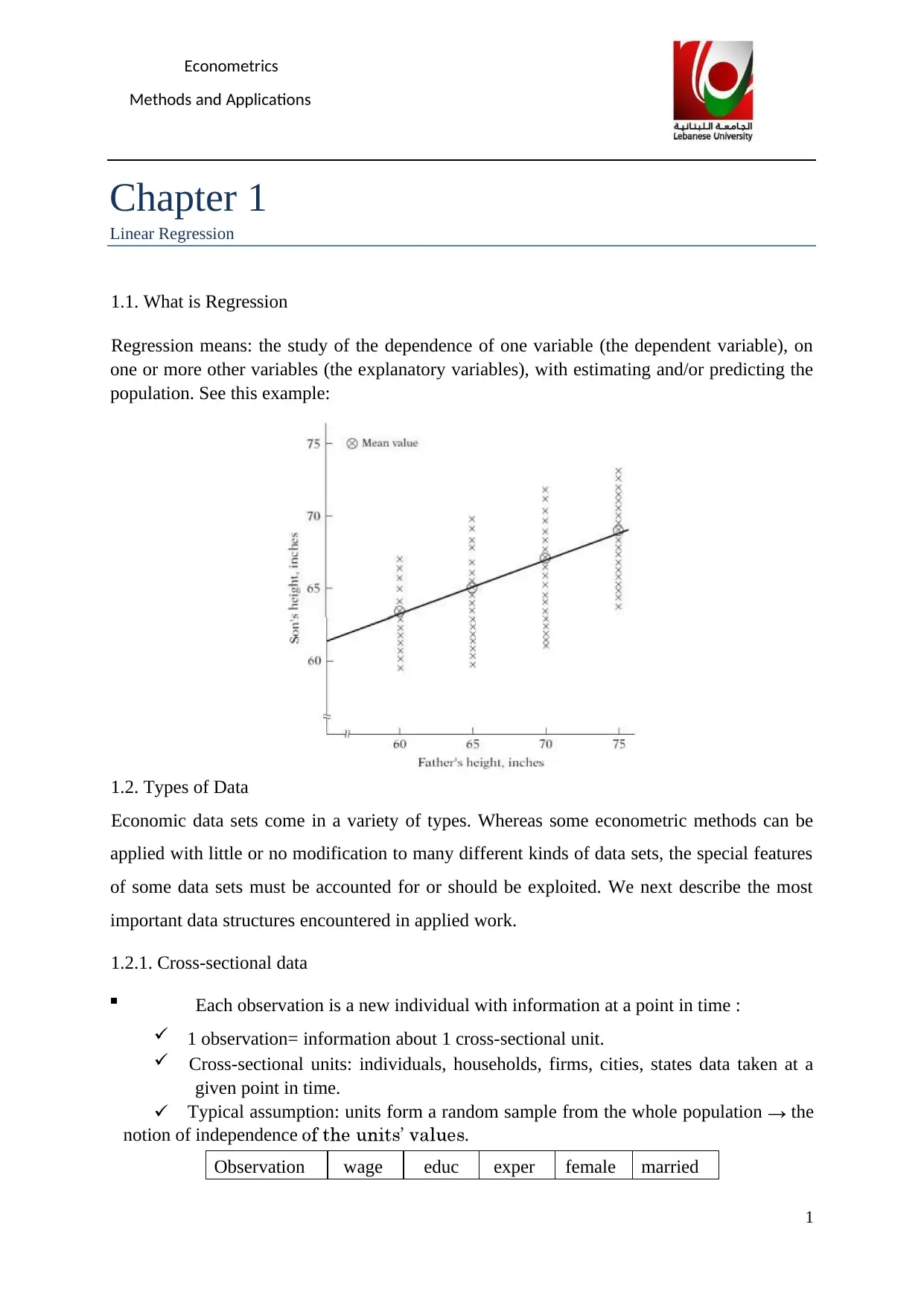
1.1. What is Regression
Regression means: the study of the dependence of one variable (the dependent variable), on
one or more other variables (the explanatory variables), with estimating and/or predicting the
population. See this example:
1.2. Types of Data
Economic data sets come in a variety of types. Whereas some econometric methods can be
applied with little or no modification to many different kinds of data sets, the special features
of some data sets must be accounted for or should be exploited. We next describe the most
important data structures encountered in applied work.
1.2.1. Cross-sectional data
Each observation is a new individual with information at a point in time :
1 observation= information about 1 cross-sectional unit.
Cross-sectional units: individuals, households, firms, cities, states data taken at a
given point in time.
Typical assumption: units form a random sample from the whole population the
notion of independence .
Observation wage educ exper female married
1
Econometrics
Methods and Applications
Linear Regression
1.1. What is Regression
Regression means: the study of the dependence of one variable (the dependent variable), on
one or more other variables (the explanatory variables), with estimating and/or predicting the
population. See this example:
1.2. Types of Data
Economic data sets come in a variety of types. Whereas some econometric methods can be
applied with little or no modification to many different kinds of data sets, the special features
of some data sets must be accounted for or should be exploited. We next describe the most
important data structures encountered in applied work.
1.2.1. Cross-sectional data
Each observation is a new individual with information at a point in time :
1 observation= information about 1 cross-sectional unit.
Cross-sectional units: individuals, households, firms, cities, states data taken at a
given point in time.
Typical assumption: units form a random sample from the whole population the
notion of independence .
Observation wage educ exper female married
1
Econometrics
Methods and Applications
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1 3.10 11 2 1 0
2 3.24 12 22 1 1
525 11.56 16 5 0 0
526 3.5 14 5 1 0
If the data is not a random sample, we have a sample selection problem
1.2.2. Time series data
Observations on economic variables over time
stock prices, money supply, CPI, GDP, annual homicide rates, automobile sales
frequencies: daily, weekly, monthly, quarterly, annually Unlike cross-
sectional data, ordering is important here!
typically, observations cannot be considered independent across time
year T-bill inflation population
2004 4.95 2.6 260,660
2005 5.21 2.8 263,034
1.2.3. Panel (or Longitudinal) data
Panel data or longitudinal data[1][2] are multi-dimensional data involving measurements over
time. Panel data contain observations of multiple phenomena obtained over multiple time
periods for the same individuals
unit year popul murders unemp police
1 2008 293,700 5 6.3 358
1 2010 299,500 7 7.4 396
2 2008 53,450 2 7.2 51
2 2010 51,970 1 8.1 51
1.3. Statistics
1.3.1. Arithmetic Mean
To obtain the value of the arithmetic mean, calculate the sum of the data and divide the result
by the total number of data. X is the symbol of the arithmetic mean.
2
2 3.24 12 22 1 1
525 11.56 16 5 0 0
526 3.5 14 5 1 0
If the data is not a random sample, we have a sample selection problem
1.2.2. Time series data
Observations on economic variables over time
stock prices, money supply, CPI, GDP, annual homicide rates, automobile sales
frequencies: daily, weekly, monthly, quarterly, annually Unlike cross-
sectional data, ordering is important here!
typically, observations cannot be considered independent across time
year T-bill inflation population
2004 4.95 2.6 260,660
2005 5.21 2.8 263,034
1.2.3. Panel (or Longitudinal) data
Panel data or longitudinal data[1][2] are multi-dimensional data involving measurements over
time. Panel data contain observations of multiple phenomena obtained over multiple time
periods for the same individuals
unit year popul murders unemp police
1 2008 293,700 5 6.3 358
1 2010 299,500 7 7.4 396
2 2008 53,450 2 7.2 51
2 2010 51,970 1 8.1 51
1.3. Statistics
1.3.1. Arithmetic Mean
To obtain the value of the arithmetic mean, calculate the sum of the data and divide the result
by the total number of data. X is the symbol of the arithmetic mean.
2
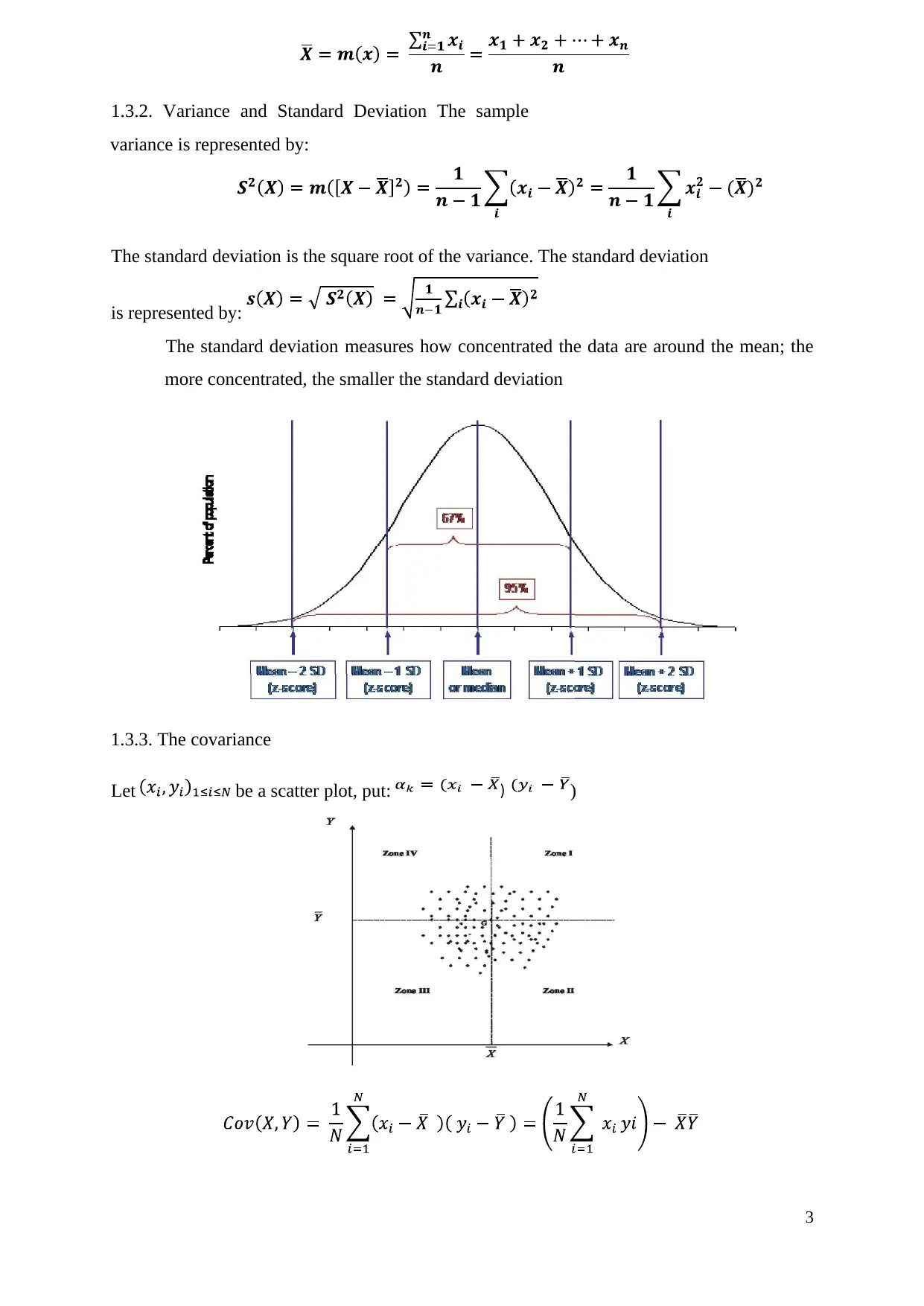
1.3.2. Variance and Standard Deviation The sample
variance is represented by:
The standard deviation is the square root of the variance. The standard deviation
is represented by:
The standard deviation measures how concentrated the data are around the mean; the
more concentrated, the smaller the standard deviation
1.3.3. The covariance
Let be a scatter plot, put: )
3
)
variance is represented by:
The standard deviation is the square root of the variance. The standard deviation
is represented by:
The standard deviation measures how concentrated the data are around the mean; the
more concentrated, the smaller the standard deviation
1.3.3. The covariance
Let be a scatter plot, put: )
3
)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

=
In the general case, this formula is written like this:
Properties
Var(a)=0; Var(aX) = a2 Var (X); Var(X+a) = Var(X)
Cov(X,X) = Var(X, X)
Cov(X,Y ) = Cov(Y,X) (Symmetry of covariance)
Cov(aX + b, Y ) = a·cov(X,Y ) (Linearity with respect to X)
Cov(X, aY + b) = a·cov(X,Y ) (Linearity with respect to Y)
Var(X+Y) = Var(X) + Var(Y) + 2 Cov (X, Y)
If X and Y are independent then Cov(X, Y) = 0
1.3.4.. Coefficient of linear correlation (Pearson coefficient)
1.4. Simple linear Regression
Simple linear regression is the most commonly used technique for determining how one
variable of interest (the response variable) is affected by changes in another variable. The
terms "response" and "explanatory" mean the same thing as "dependent" and "independent",
but the former terminology is preferred because the "independent" variable may actually be
interdependent with many other variables as well. Simple linear regression is used for three
main purposes:
To describe the linear dependence of one variable on another.
To predict values of one variable from values of another, for which more data are
available.
To correct for the linear dependence of one variable on another, in order to clarify other
features of its variability. Linear regression determines the bestfit line through a scatter
plot of data, such that the sum of squared residuals is minimized; equivalently, it
4
In the general case, this formula is written like this:
Properties
Var(a)=0; Var(aX) = a2 Var (X); Var(X+a) = Var(X)
Cov(X,X) = Var(X, X)
Cov(X,Y ) = Cov(Y,X) (Symmetry of covariance)
Cov(aX + b, Y ) = a·cov(X,Y ) (Linearity with respect to X)
Cov(X, aY + b) = a·cov(X,Y ) (Linearity with respect to Y)
Var(X+Y) = Var(X) + Var(Y) + 2 Cov (X, Y)
If X and Y are independent then Cov(X, Y) = 0
1.3.4.. Coefficient of linear correlation (Pearson coefficient)
1.4. Simple linear Regression
Simple linear regression is the most commonly used technique for determining how one
variable of interest (the response variable) is affected by changes in another variable. The
terms "response" and "explanatory" mean the same thing as "dependent" and "independent",
but the former terminology is preferred because the "independent" variable may actually be
interdependent with many other variables as well. Simple linear regression is used for three
main purposes:
To describe the linear dependence of one variable on another.
To predict values of one variable from values of another, for which more data are
available.
To correct for the linear dependence of one variable on another, in order to clarify other
features of its variability. Linear regression determines the bestfit line through a scatter
plot of data, such that the sum of squared residuals is minimized; equivalently, it
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

minimizes the error variance. The fit is "best" in precisely that sense: the sum of squared
errors is as small as possible. That is why it is also termed "Ordinary Least Squares"
regression. Model of the simple linear regression is given by:
Simple regression = regression with 2 variables: Yt 1Xt + t
Yt Xt
Dependent variable Independent variable
Explained variable Explanatory variable
Response variable Control variable
Predicted variable Predictor variable
Regressand Regressor
0: Intercept (is the estimate of the mean outcome when x = 0 and should always be
stated in terms of the actual variables of the study)
1: the slope coefficient (The interpretation of 1
explanatory variable increases by one unit. This should always be stated in terms of the
actual variables of the study).
t: specification error (difference between the true model and the specified model).
An important objective of regression analysis is to estimate the unknown parameters 0 and
1 in the regression model. This process is also called fitting the model to the data, the
parameters 0 and 1 are usually called regression coefficients. The slope 1 is the change in
the mean of the distribution of Y producing a unit change in X. The intercept 0 is the mean
of the distribution of the response variable Y when X=0.
We are actually going to derive the linear regression model in three very different ways
these three ways reflect three types of econometric questions : descriptive, causal and
forecasting
1.5. Descriptive Analysis
Estimate E[y|x] (called the population regression function). In other words, we
5
0
errors is as small as possible. That is why it is also termed "Ordinary Least Squares"
regression. Model of the simple linear regression is given by:
Simple regression = regression with 2 variables: Yt 1Xt + t
Yt Xt
Dependent variable Independent variable
Explained variable Explanatory variable
Response variable Control variable
Predicted variable Predictor variable
Regressand Regressor
0: Intercept (is the estimate of the mean outcome when x = 0 and should always be
stated in terms of the actual variables of the study)
1: the slope coefficient (The interpretation of 1
explanatory variable increases by one unit. This should always be stated in terms of the
actual variables of the study).
t: specification error (difference between the true model and the specified model).
An important objective of regression analysis is to estimate the unknown parameters 0 and
1 in the regression model. This process is also called fitting the model to the data, the
parameters 0 and 1 are usually called regression coefficients. The slope 1 is the change in
the mean of the distribution of Y producing a unit change in X. The intercept 0 is the mean
of the distribution of the response variable Y when X=0.
We are actually going to derive the linear regression model in three very different ways
these three ways reflect three types of econometric questions : descriptive, causal and
forecasting
1.5. Descriptive Analysis
Estimate E[y|x] (called the population regression function). In other words, we
5
0

6
f in E[ y| x ] = f(x ):
The simplest model is E[ y| x ] = 0 + 1 x
f in E[ y| x ] = f(x ):
The simplest model is E[ y| x ] = 0 + 1 x
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
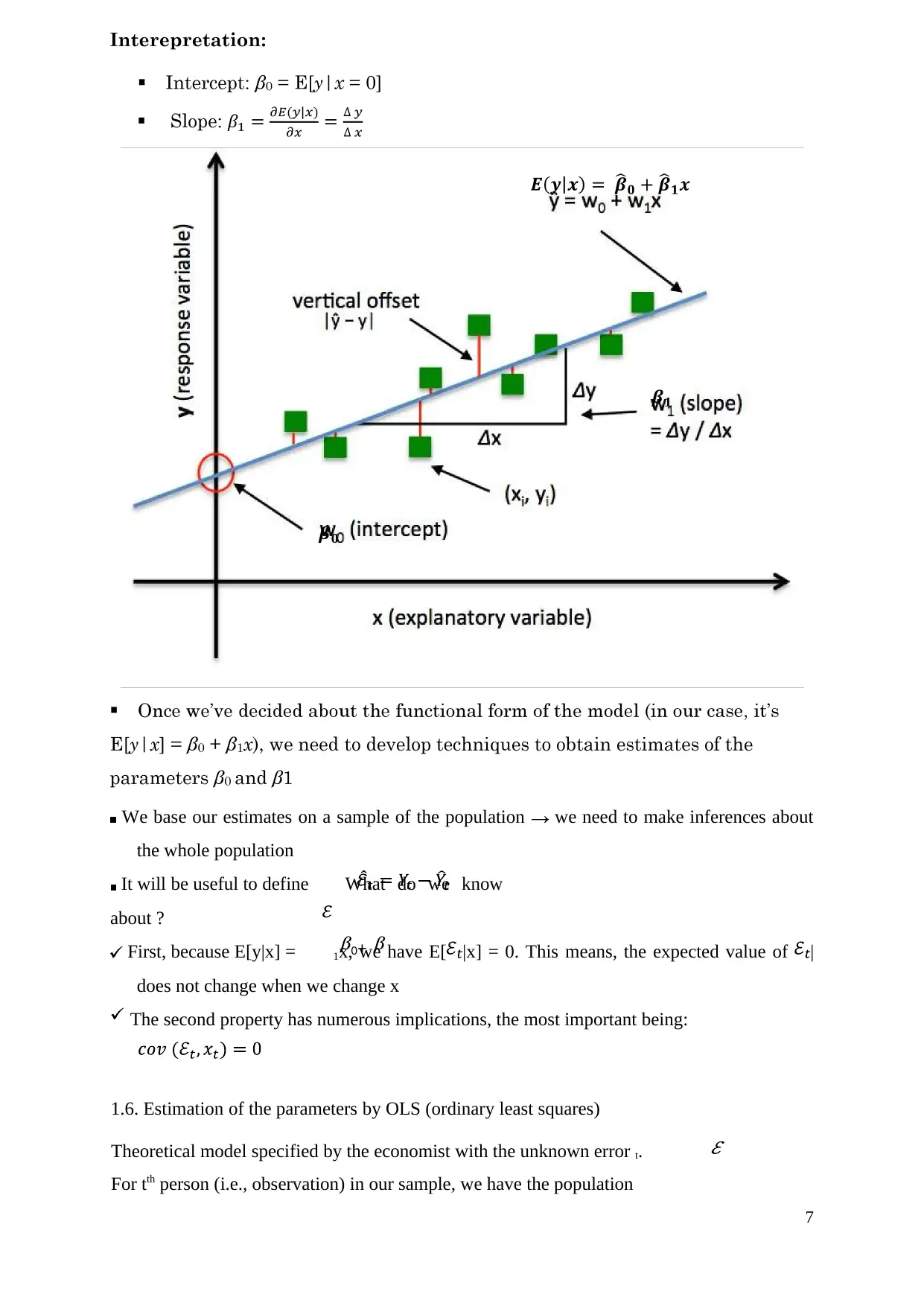
0+
We base our estimates on a sample of the population we need to make inferences about
the whole population
It will be useful to define What do we know
about ?
First, because E[y|x] = 1x, we have E[ |x] = 0. This means, the expected value of |
does not change when we change x
The second property has numerous implications, the most important being:
1.6. Estimation of the parameters by OLS (ordinary least squares)
Theoretical model specified by the economist with the unknown error t.
For tth person (i.e., observation) in our sample, we have the population
7
We base our estimates on a sample of the population we need to make inferences about
the whole population
It will be useful to define What do we know
about ?
First, because E[y|x] = 1x, we have E[ |x] = 0. This means, the expected value of |
does not change when we change x
The second property has numerous implications, the most important being:
1.6. Estimation of the parameters by OLS (ordinary least squares)
Theoretical model specified by the economist with the unknown error t.
For tth person (i.e., observation) in our sample, we have the population
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Regression model
The observed residual is the difference between the observed values and the adjusted value
using estimates of the dependent variable using estimates of model coefficients:
we want this to be min but could be zero since the points are up
Using OLS, we minimize
Ordinary least squares (OLS) or linear least squares is a method for estimating the unknown
parameters in a linear regression model. This method minimizes the sum of squared error or
residual. Mathematically the sum of square of error can be:
8
The observed residual is the difference between the observed values and the adjusted value
using estimates of the dependent variable using estimates of model coefficients:
we want this to be min but could be zero since the points are up
Using OLS, we minimize
Ordinary least squares (OLS) or linear least squares is a method for estimating the unknown
parameters in a linear regression model. This method minimizes the sum of squared error or
residual. Mathematically the sum of square of error can be:
8

Simplifying the above equations we get the following normal equations:
(II)
(III)
are based on a single sample rather than the entire population. If you took different sample,
you would get different values for
the OLS estimators of 0 and 1. One of the main goals of econometrics is to analyze the
quality of these estimators and see under what conditions these are good estimators and under
which conditions they are not.
Properties of Least -Square Estimators:
I. The OLS estimators are expressed solely in terms of the observable (i.e., sample)
quantities (i.e., X and Y). Therefore, they can be easily computed.
II. They are point estimators; that is, given the sample, each estimator will provide only
a single (point) value of the relevant population parameter.
9
and and
(II)
(III)
are based on a single sample rather than the entire population. If you took different sample,
you would get different values for
the OLS estimators of 0 and 1. One of the main goals of econometrics is to analyze the
quality of these estimators and see under what conditions these are good estimators and under
which conditions they are not.
Properties of Least -Square Estimators:
I. The OLS estimators are expressed solely in terms of the observable (i.e., sample)
quantities (i.e., X and Y). Therefore, they can be easily computed.
II. They are point estimators; that is, given the sample, each estimator will provide only
a single (point) value of the relevant population parameter.
9
and and
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
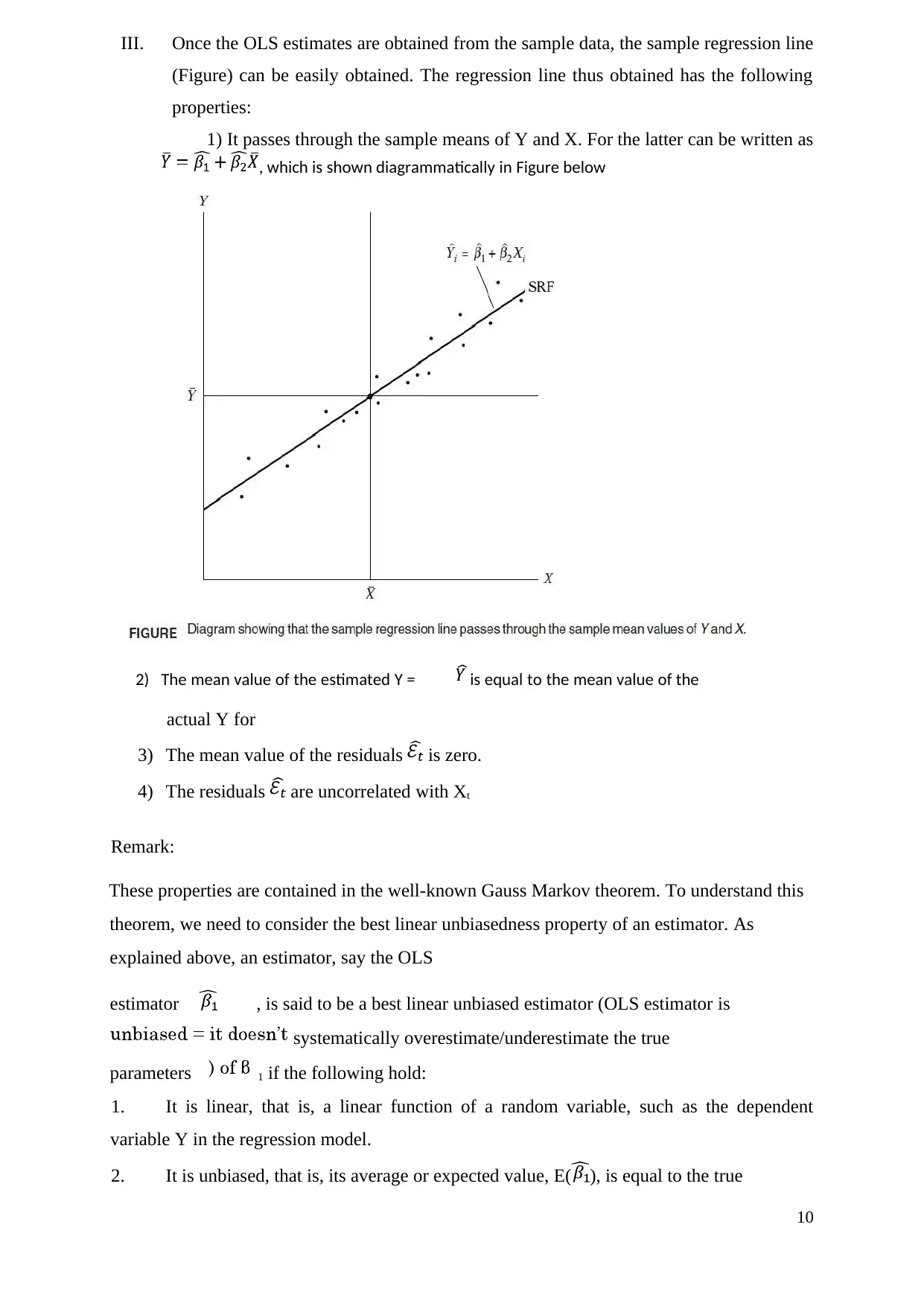
III. Once the OLS estimates are obtained from the sample data, the sample regression line
(Figure) can be easily obtained. The regression line thus obtained has the following
properties:
1) It passes through the sample means of Y and X. For the latter can be written as
actual Y for
3) The mean value of the residuals is zero.
4) The residuals are uncorrelated with Xt
Remark:
These properties are contained in the well-known Gauss Markov theorem. To understand this
theorem, we need to consider the best linear unbiasedness property of an estimator. As
explained above, an estimator, say the OLS
estimator , is said to be a best linear unbiased estimator (OLS estimator is
systematically overestimate/underestimate the true
parameters 1 if the following hold:
1. It is linear, that is, a linear function of a random variable, such as the dependent
variable Y in the regression model.
2. It is unbiased, that is, its average or expected value, E( ), is equal to the true
10
, which is shown diagrammatically in Figure below
2) The mean value of the estimated Y = is equal to the mean value of the
(Figure) can be easily obtained. The regression line thus obtained has the following
properties:
1) It passes through the sample means of Y and X. For the latter can be written as
actual Y for
3) The mean value of the residuals is zero.
4) The residuals are uncorrelated with Xt
Remark:
These properties are contained in the well-known Gauss Markov theorem. To understand this
theorem, we need to consider the best linear unbiasedness property of an estimator. As
explained above, an estimator, say the OLS
estimator , is said to be a best linear unbiased estimator (OLS estimator is
systematically overestimate/underestimate the true
parameters 1 if the following hold:
1. It is linear, that is, a linear function of a random variable, such as the dependent
variable Y in the regression model.
2. It is unbiased, that is, its average or expected value, E( ), is equal to the true
10
, which is shown diagrammatically in Figure below
2) The mean value of the estimated Y = is equal to the mean value of the
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

value, 1 : E( ) 1
and
So
3. It has minimum variance in the class of all such linear unbiased estimators; an
unbiased estimator with the least variance is known as an efficient estimator.
(Best Linear Unbiased Estimator)
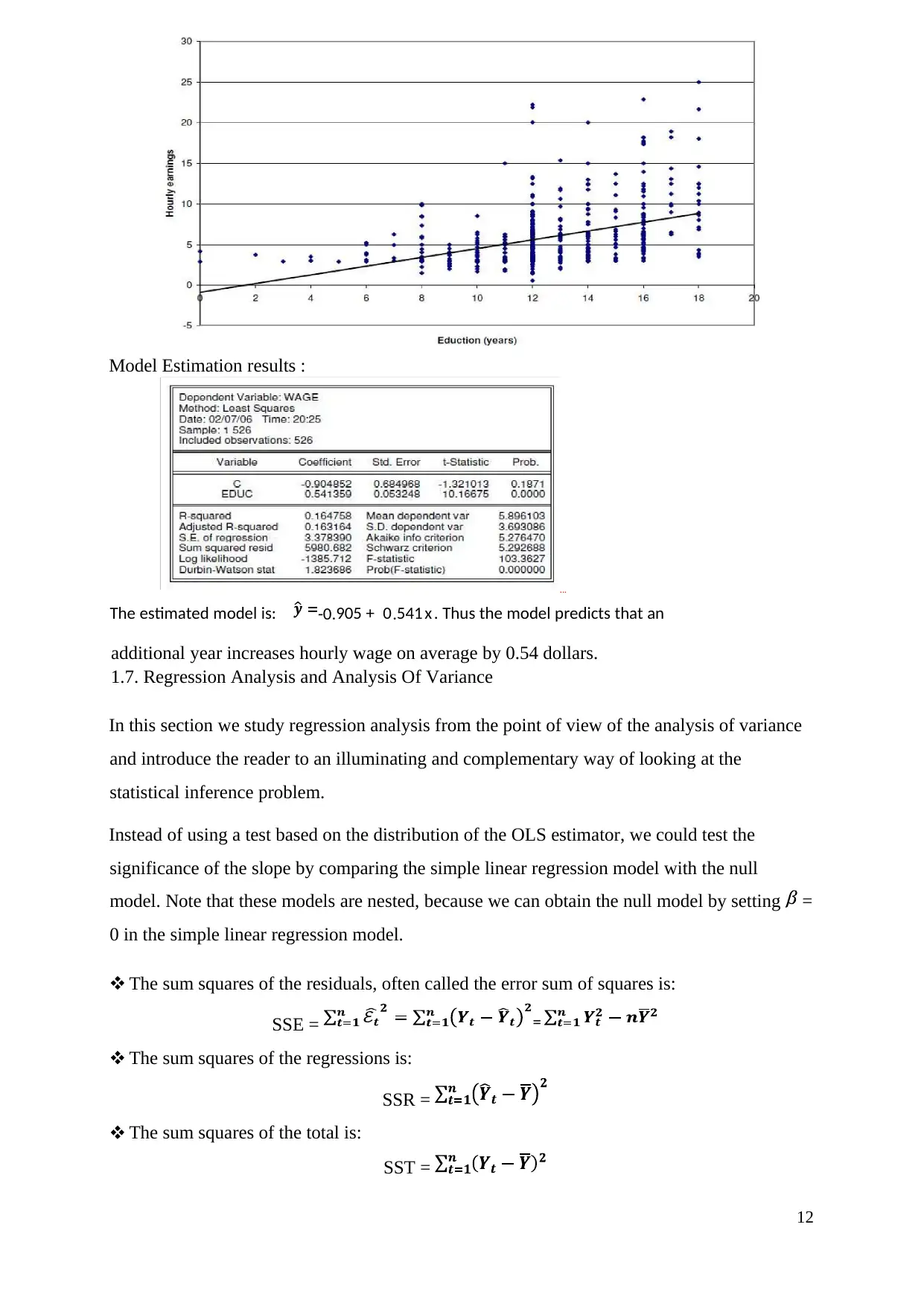
Example 1: Relationship between wage and eduction. wage =
average hourly earnings educ = years of education
Data is collected in 1976, n = 526
...
Figure: Scatter plot of the data with regression line.
11
and
So
3. It has minimum variance in the class of all such linear unbiased estimators; an
unbiased estimator with the least variance is known as an efficient estimator.
(Best Linear Unbiased Estimator)
Example 1: Relationship between wage and eduction. wage =
average hourly earnings educ = years of education
Data is collected in 1976, n = 526
...
Figure: Scatter plot of the data with regression line.
11
Model Estimation results :
additional year increases hourly wage on average by 0.54 dollars.
1.7. Regression Analysis and Analysis Of Variance
In this section we study regression analysis from the point of view of the analysis of variance
and introduce the reader to an illuminating and complementary way of looking at the
statistical inference problem.
Instead of using a test based on the distribution of the OLS estimator, we could test the
significance of the slope by comparing the simple linear regression model with the null
model. Note that these models are nested, because we can obtain the null model by setting =
0 in the simple linear regression model.
The sum squares of the residuals, often called the error sum of squares is:
SSE =
The sum squares of the regressions is:
SSR =
The sum squares of the total is:
SST =
12
...
The estimated model is: -0.905 + 0.541 x . Thus the model predicts that an
=
additional year increases hourly wage on average by 0.54 dollars.
1.7. Regression Analysis and Analysis Of Variance
In this section we study regression analysis from the point of view of the analysis of variance
and introduce the reader to an illuminating and complementary way of looking at the
statistical inference problem.
Instead of using a test based on the distribution of the OLS estimator, we could test the
significance of the slope by comparing the simple linear regression model with the null
model. Note that these models are nested, because we can obtain the null model by setting =
0 in the simple linear regression model.
The sum squares of the residuals, often called the error sum of squares is:
SSE =
The sum squares of the regressions is:
SSR =
The sum squares of the total is:
SST =
12
...
The estimated model is: -0.905 + 0.541 x . Thus the model predicts that an
=
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 22
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





