MOD005790 Research Project: Beam Analysis and MATLAB Solution
VerifiedAdded on 2023/04/19
|7
|548
|103
Project
AI Summary
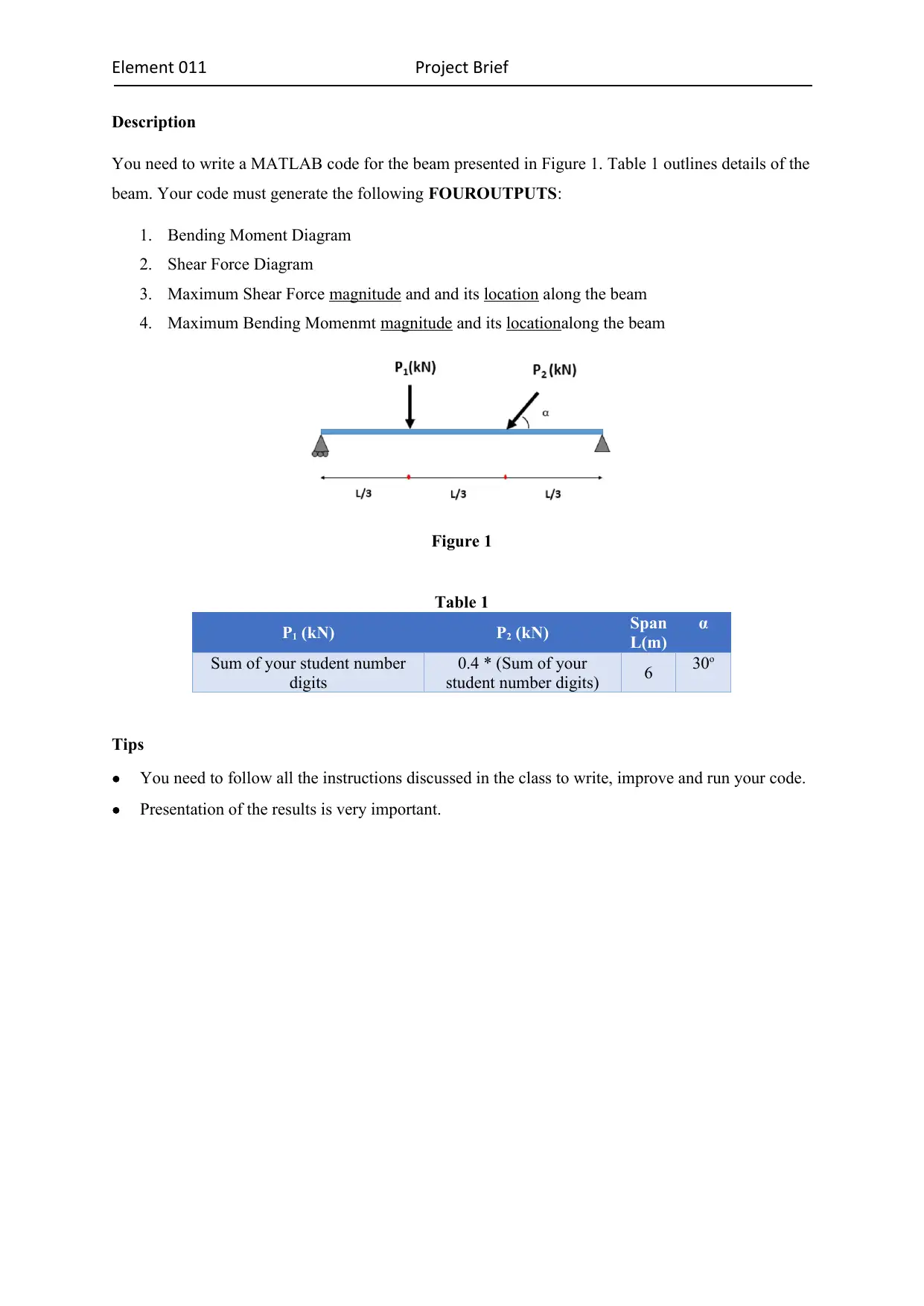
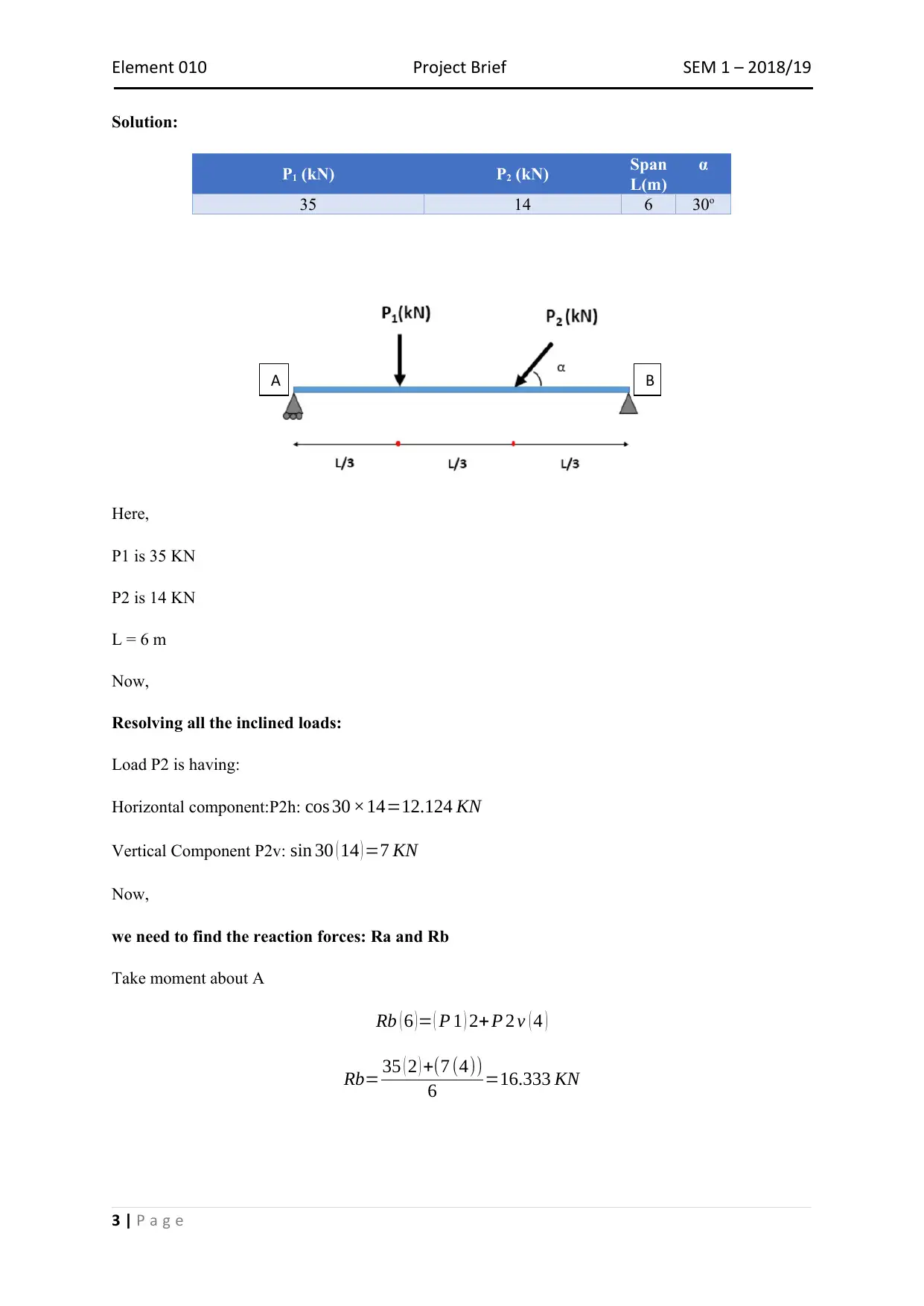
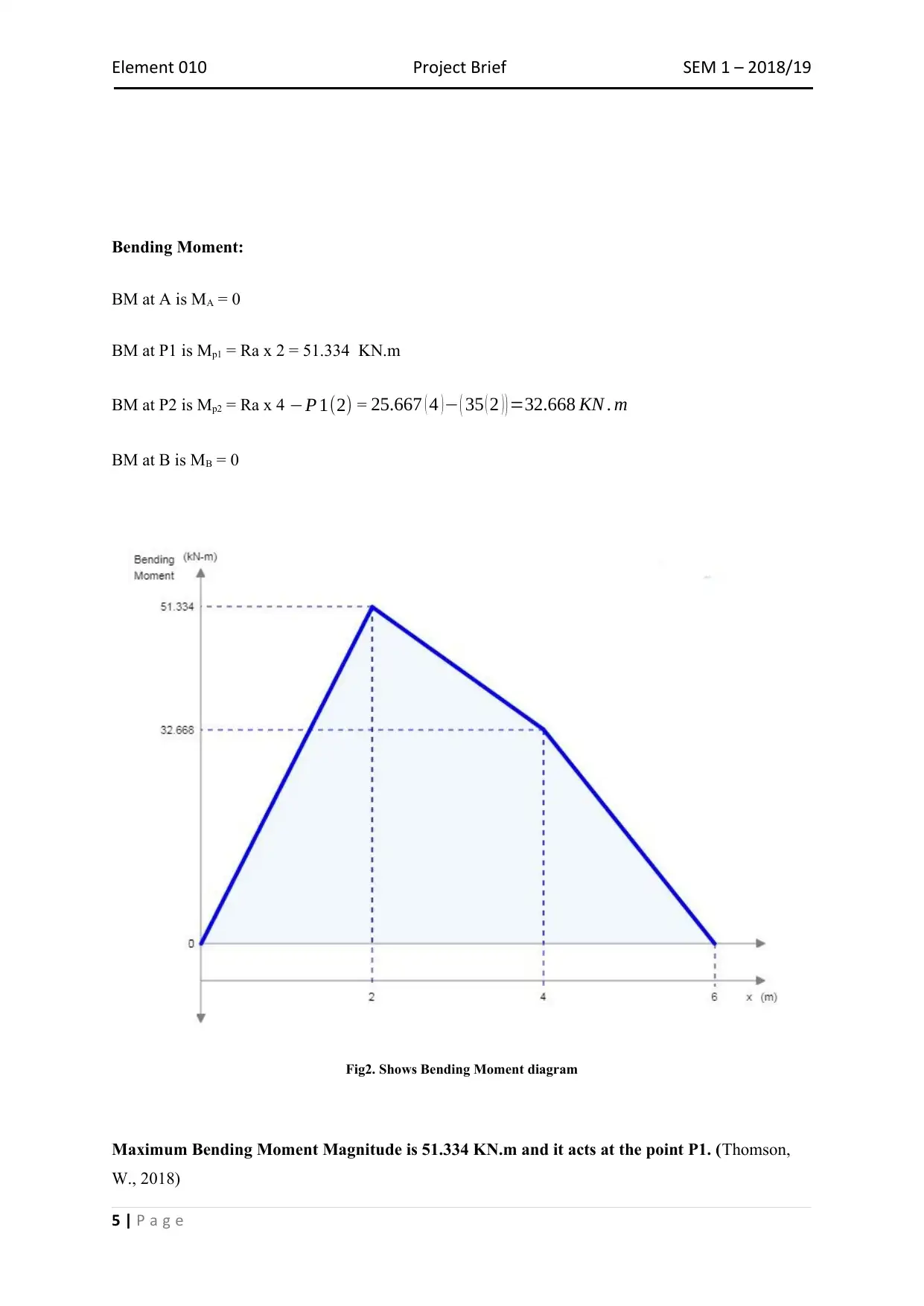
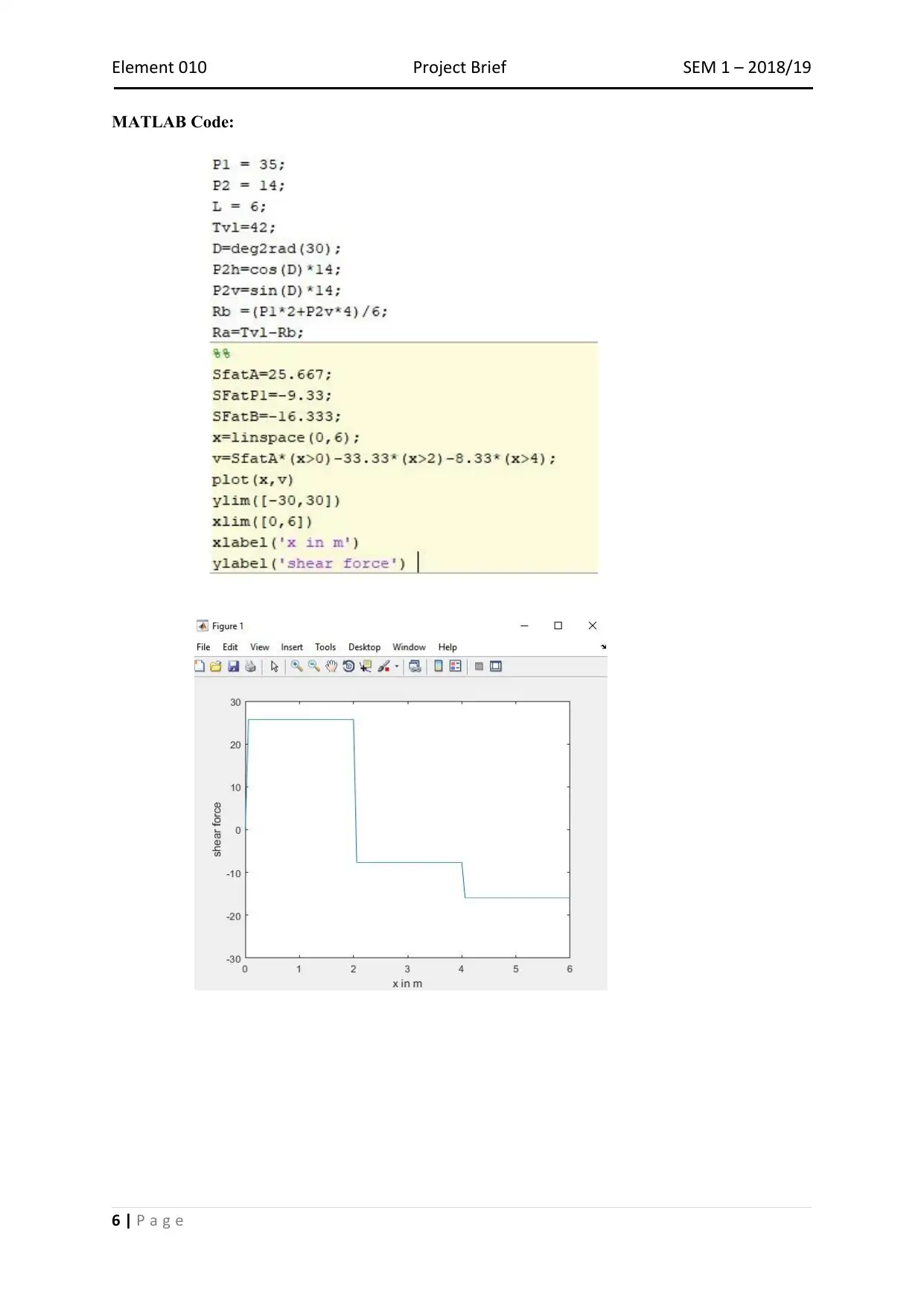
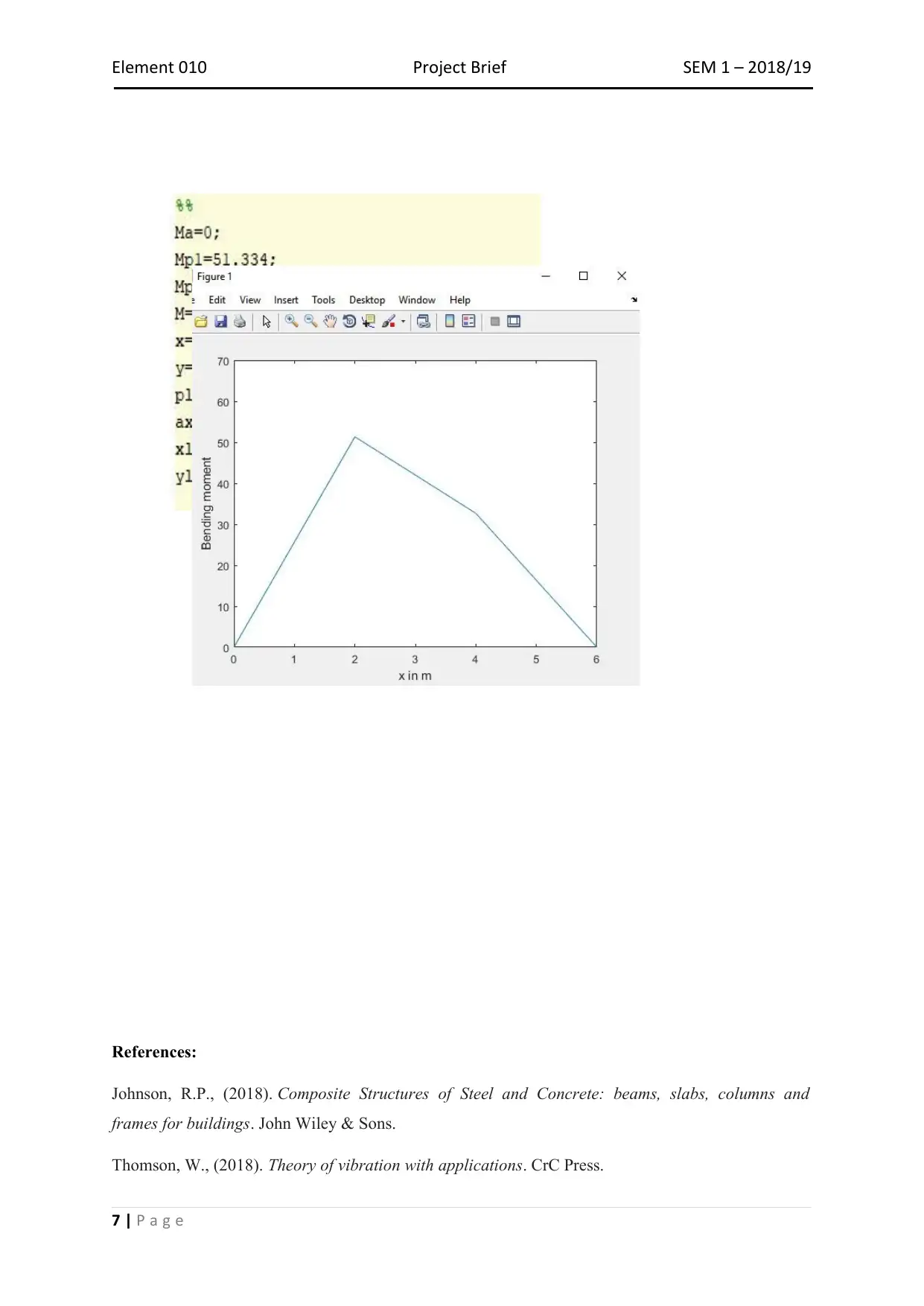
This document presents a solution to a project brief requiring MATLAB code for beam analysis. The solution includes the calculation of reaction forces, shear force diagrams, bending moment diagrams, and the determination of maximum shear force and bending moment magnitudes along with their locations. The document provides the MATLAB code used for the analysis and presents the resulting diagrams and calculations. This project showcases the application of computational methods in solving structural engineering problems. Desklib offers a wide array of similar solved assignments and past papers for students seeking assistance with their studies.
1 out of 7





![[object Object]](/_next/static/media/star-bottom.7253800d.svg)