Energy Systems Lab Assignment 2022

ENERGY SYSTEMS LAB
Name of student
Institution
Date

Table of Contents
Introduction......................................................................................................................................3
Methodology....................................................................................................................................4
Development of the theoretical model.............................................................................................5
Experimental setup and measurements model.................................................................................5
Results analysis................................................................................................................................6
Sensitivity analysis..........................................................................................................................6
Theoretical model............................................................................................................................6
Theory and equations.......................................................................................................................6
Experimental set-up.......................................................................................................................10
Equipment’s...................................................................................................................................10
Procedure:......................................................................................................................................11
Assumptions..................................................................................................................................13
Result and discussion:....................................................................................................................13
Experimental data..........................................................................................................................13
Graphical data................................................................................................................................15
Discussion......................................................................................................................................20
Conclusions....................................................................................................................................21
References......................................................................................................................................22

Introduction
As stated in the above laboratory experiment objective, a Cussons P1740 solar heating apparatus is to be used to
show how heat from solar energy is obtained as well as its efficiency in capturing heat. The diagram shown below
indicates the Cussons P1740 solar heating apparatus. It includes a shallow heat collection tray including a base that is
attached to a removable heat capture material that is significant during the heat transfer process (Costa et al., 2016). A flat
plate glass material is then utilized to cover the transfer plate, which also performs the duty of capturing the radiated heat
present on top of the heating lamps and then reflect it back.
The heat transfer plate as well acts as passage surface for the water which is pumped to the tray and then taken
back via the base of the unit to the insulated reservoir. This water gets circulated in a repeated manner inside the transfer
plate, in order to intensify the temperature in the reservoir. The aluminium fins are significant in offering water to the
wall to ensure extreme transfer of heat (Ohta, 2013). The speed at which water flows from the feed can not only be
regulated but also determined. when this occurs, various amounts of water exposure are allowed to the heated tray. The
mounting of the unit allows for tilting of the base between +10o horizontally, hence enabling an adjustment of the tray.
There is a total of eight thermocouples, which are utilized for determining the water temperature, and the
thermocouples are attached to a selector switch. The selector switch output, in turn, is attached to the data capture pc. The
labelling of the thermocouples is done statistically and they determine he temperatures at the below points air space in the
tray, upper panel surface, water outside the solar panel, water reservoir temperature, water inside the solar panel, the
ambient air, lower lass surface as well as the upper glass surface.
Objective
Majorly, this laboratory experiment aim at demonstrating the principle of solar energy collection through the
utilization of Cussons P1740 solar heating apparatus. The apparatus is designated to show how heat is captured from a
solar energy unit and then the illustration of the relative efficiency with respect to the theoretical one provided.
Methodology
The diagram below shows the design methodology of the entire laboratory experiment, which has so far been
separated into five sections. These sections assist in determining how the various operating parameters influence the
efficiency of the solar collector apparatus for water heating systems. In the first block, the idea is to have a theoretical

model, which is with regards to the existing literary knowledge. In the second block, a description of the experimental
activity which was conducted has been detailed. This is then proceeded by analysis of data which has been extracted from
the above three blocks. Further analysis is done in the fourth block and then followed by a block detailing the effects of
the operational parameters on the efficiency of the solar collector apparatus
Development of the theoretical model
The theoretical model basically aims at creating a better comprehension of the general solar collector as well as
how it is affected by various operational parameters. The model gives a detailed explanation of how the transfer of heat
takes place in solar collectors, by proving additional equations to supplement the knowledge. The equations were with
regards to the information already existing in research articles related to solar energy. This theoretical model was
significant as it was used in analysing the experimental measurements which have been obtained.
Experimental setup and measurements model
In this stage, the base structure of the solar collector was being modelled. At this stage, certain measurements
were recorded to assess the performance of the solar collector apparatus. In order to understand the effect of flow rate on
the efficiency, the readings were taken every two minutes for ten rounds. These readings included the inlet temperatures,
outlet temperatures, sun peak hours as well as the temperature of the tank.
To determine the implication of the tilt angle on the efficiency, the rate of flow was kept at a constant value, and
thus only the angle being varied and readings taken. . These readings included the inlet temperatures, outlet temperatures,
sun peak hours as well as the temperature of the tank.

Results analysis
The analysis of the data was with respect to the two above blocks. A comparison of the theoretical and
experimental results was made and then the discussion formulated. The conclusion was then done with regards to the
effects of various parameters on the performance of the solar apparatus.
Sensitivity analysis
This analysis was done based on the various computations and assumptions, which have affected the overall
outcome of the experiment. To fully realise the difference, the data obtained was altered a bit, but one at a time. This
allowed for analysis of deviations in the final outcome.
Theoretical model
Theory and equations
From the source of solar radiation and light comes in the form of optical wavelengths, and as they pass through
the crystal clear cover, they get reflected back at infrared wavelengths from the opaque cover, hence trapped light energy.
In order to conduct the analysis, the heater is segregated into two thermal divisions, the first being the cover section while
the second one the solar panel. Applying the nomenclature illustrated in the second figure, the energy balances can be
depicted as shown below
Energy balance for the cover
 g Q  qrwg  qcga  qrga ……………………..(1) (Sinha and Chandel, 2014)
Where  g Q is the radiant heat which is absorbed by the cover
Q - the incident radiation
 g – the absorptivity of the cover
qrwg radiant heat flow from the solar panel to to the cover
qcga – the heayt lost by the cover from convection
qrga - the heayt lost by the cover from radiation
for the solar panel

 w t g Q  qwtr + qrwg + qb + Cm
Tm /
T …………………………….. (2)
where
 w t g Q - the radiant energy absorbed by the solar panel
qwtr
the heat transferred to the water to give the temperature rise across the panel,
t g - transmissivity of the cover
 w - the absorptivity of the panel and the material,
Qb - the conduction heat loss from the base,
Cm
Tm /
T - thermal lag term for unsteady operation
Tm - the mean mat temperature
The heat which is transferred to the a=water cvan be obtained by adopting the below changes :
Twoi  Two  Twi
qwtr  m cw  Two  Twi   m cw Twoi …………………………………..(3) (Green et al., 2015)
where;
m - is the mass flow rate of the water over the solar panel in kg / s.
cw - is the specific heat capacity of the water.
A combination of conduction and radiation is responsible fo the transfer of heat back to the panel. This
can be noted in the below form;
………….(4) (Pfenninger et al., 2014)
where
Tw and Tg - absolute temperatures of the gas and water which is stuck between the cover and the panel
 w - the emissivity of the brine surface
 - the Stefan-Boltzmann constant  56.69 1012 kJ / m2 K 4 s.

rg
a
g
Thus, the convective heat loss;
qcga  hcga Tga……………………………………………….. (5)
where ;
Tga - the temperature difference between the ambient air ( Ta ) and the trapped gas ( Tg )
hcga - the heat transfer coefficient, which relies on the velocity of the wind
Assuming that the sky is modelled with a temperature of approximately 11K lower than the 0.9 ambient emittances, the
heat lost from the sky by radiation is obtained in the following manner;
q  0.9
 T 4  T 11 4   3.6
 T 3  T 11 (6)
the expression of the base loss is shown below
qb  hb T w  T a  ………………………(7)
In between the ground and the base, there exists a heat transfer coefficient hbo, whose average is approximately 33kJ /
m2 hK, that’s if we do not factor in the insulation aspects. However, it is recommended to apply some form of base loss
and insulation coefficient, which is obtained in the following manner;
……………………………………………(8) (Harish and Kumar, 2016)
Where
k - conductivity.
d - the insulation depth
Since we are equipped with the various terms of the thermal transfer, we can determine the heater efficiency as well as its
performance implications by the various factors of variation. For certain solar radiation, Q with known ambient
a

temperature, Ta , the first and second equations can be determined simultaneously for Twg and Tga. The function
below indicates the variation of insolation during the daytime.
Q  Qmax cos

Where
 - the angle of incidence
Qmax - 3.288kJ / m2h .
For thermal efficny, the equation below defines it:
………………………(10)
When we substitute qwtr from equations one and two above of the energy balances of the solar panel and the
cover, will be at a position to determine the theoretical efficiency of the panel. Either the variation between the theoretical
and the obtained values offers us with a chance for discussion on the assumptions, which were made, or on the factors
which have an effect on the performance. For the case of the panel, the factors that need consideration include the
efficiency of the flow rate, and the panel temperature. The possible variation of the performance within a day and the
implications of the ambient temperature, insulation, and the wind. Furthermore, the extra requirements such as the
extraction of the amount of heat to support the water at maximum level heat it to maximum temperature are possible
(Alstone et al., 2015).
Experimental set-up
Equipment’s
 Solar panel
 Glass cover
 Pump
 Cooling coil
 Flow-meter
 An absorptive material

 Heating tray
 An insulation layer
 Reservoir
 Flow control valve
The configuration of the apparatus is as shown below
FIG. 1: Sollar collector apparatus (Bahramara et al., 2016).
Fig. 2: Energy balance nomenclature (Bahramara et al., 2016).

Procedure:
The cushions P1740 solar heating apparatus was first turned on and the adjusted from the flow control valve until
the rate of flow of water was recorded as 4 litres per minute. It was let at that point until an equilibrium of the water flow
was attained, after which, all the airlocks within the system was monitored. It was advised at this juncture that the base of
the solar panel be eliminated, which was done consequently.
After the above steps, the personal daqview computer software was begun, setting the recommended values for
the experiment. The parameters included an interval of two minutes for 11 data capture points, for a total duration of
twenty minutes. Thereafter, the heating lamps were turned on and a minute allowed to elapse, then proceeded by starting
of the logging of data in the personaldaqview. This data was then saved upon the completion of the time step.
After the above step, the insulation to the base of the solar panel, which had been initially eliminated, was
replaced back, and data logging of a new set began within the computer software. The above step was repeated, i.e. the
recommended parameters for the experiment was set for twenty minutes, followed by turning on of the heating lamps for
a minute and finally,-logging of data in the personaldaqview. This second data as well was then saved upon the
completion of the time step. Of worth noting is that the rate of flow for the two procedures was maintained at four
minutes for every minute.
Subsequently, the rate of flow was changed from four litres for every minute, to two litres for every minute and
then the water flow allowed until equilibrium was attained. This was then proceeded by logging of data. The base of the
solar panel is eliminated, which was done consequently. the recommended parameters for the experiment was set for
twenty minutes, followed by turning on of the heating lamps for a minute and finally,-logging of data in the
personaldaqview. This third set of data as well was saved upon the completion of the time step.

Thermocouples used in collecting data (Bahramara et al., 2016)
Flow-meter (Bahramara et al., 2016).
Assumptions
 The assumptions made is that the model represented in this experiment applies steady-state conditions.
The temperature of the mean absorber is the average of outlet and inlet temperature
Result and discussion:
Experimental data:
The following parameters have been noticed during the experiment.

 Table 1: Raw data
Type
-250.0 to
250.0
-15.0 to
15.0 Type K Type K Type K Type K Type K Type K Type K Type K
Units kPa l/min °C °C °C °C °C °C °C °C
Time, s Pressure Flow Panel
Reservoi
r1
GlassUp
per1
GlassLo
wer1
AirSpace
1
WaterIn
1
WaterO
ut1
Ambient
1
0000 0.312993 2.103 18.76 17.292 24.26765 20.978 18.424 17.592 19.185 17.497
120 0.296204 2.025 20.207 17.470 30.90537 27.090 20.318 17.972 19.843 17.470
240 0.306631 2.080 21.217 17.817 36.55929 32.661 21.805 18.313 20.268 17.302
360 0.294436 2.020 21.947 18.164 41.18044 37.380 22.824 18.651 20.630 17.375
480 0.290902 2.229 22.582 18.405 44.84963 41.320 23.645 18.941 20.913 17.37404
600 0.308 2.151 23.213 18.790 48.12875 44.748 24.454 19.285 21.307 17.40576
720 0.267 2.153 23.814 19.175 50.91783 47.698 25.196 19.652 21.689 17.60255
840 0.2843 2.068 24.326 19.546 53.11547 50.183 25.932 20.009 22.039 17.61688
960 0.309 2.051 24.838 19.809 55.06281 52.237 26.549 20.316 22.380 17.63243
1080 0.269 2.108 25.356 20.250 56.71954 54.100 27.194 20.642 22.731 17.65523
1200 0.288 2.1160 25.894 20.605 58.32391 55.712 27.820 21.015 23.114 17.76465

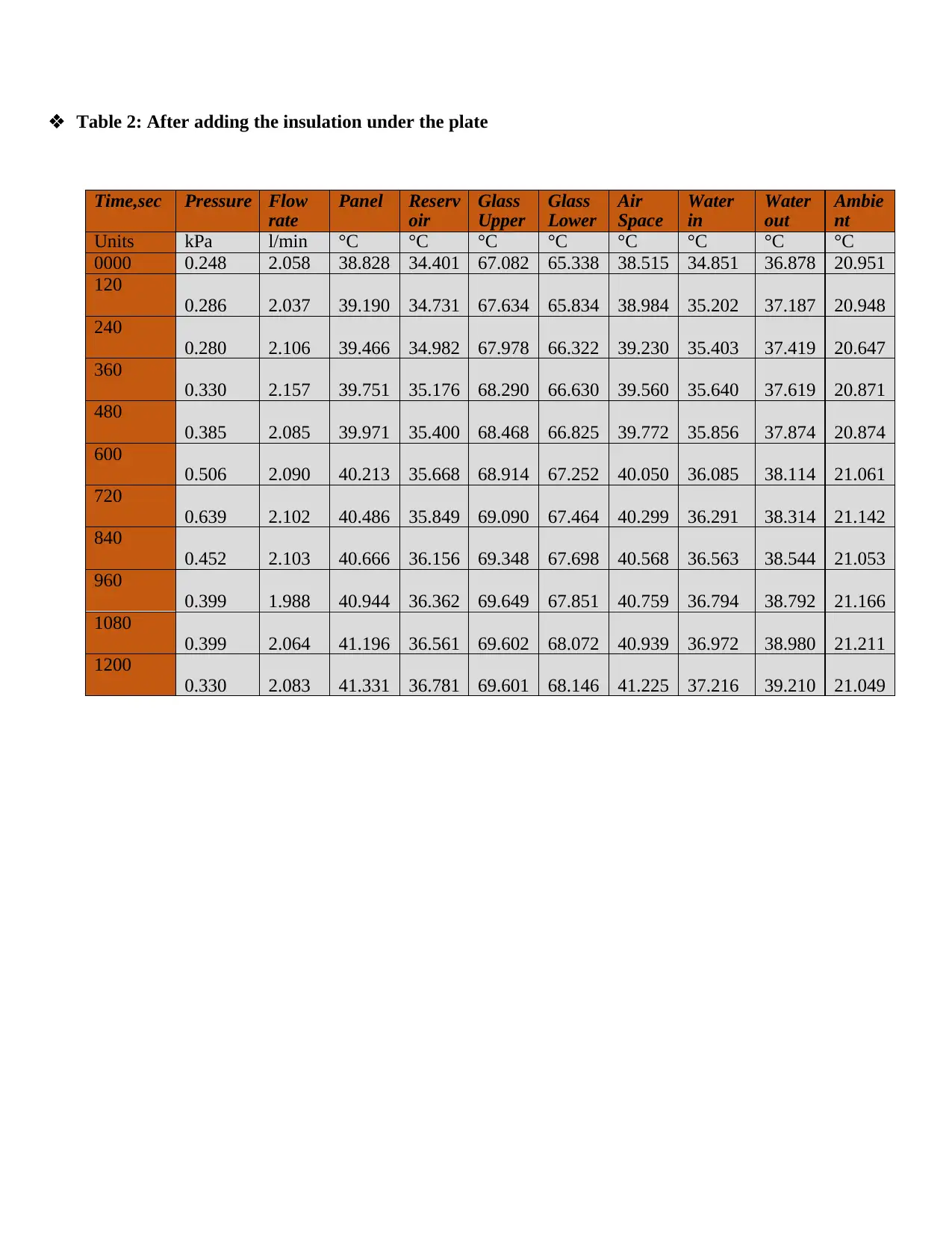
 Table 2: After adding the insulation under the plate
Time,sec Pressure Flow
rate
Panel Reserv
oir
Glass
Upper
Glass
Lower
Air
Space
Water
in
Water
out
Ambie
nt
Units kPa l/min °C °C °C °C °C °C °C °C
0000 0.248 2.058 38.828 34.401 67.082 65.338 38.515 34.851 36.878 20.951
120
0.286 2.037 39.190 34.731 67.634 65.834 38.984 35.202 37.187 20.948
240
0.280 2.106 39.466 34.982 67.978 66.322 39.230 35.403 37.419 20.647
360
0.330 2.157 39.751 35.176 68.290 66.630 39.560 35.640 37.619 20.871
480
0.385 2.085 39.971 35.400 68.468 66.825 39.772 35.856 37.874 20.874
600
0.506 2.090 40.213 35.668 68.914 67.252 40.050 36.085 38.114 21.061
720
0.639 2.102 40.486 35.849 69.090 67.464 40.299 36.291 38.314 21.142
840
0.452 2.103 40.666 36.156 69.348 67.698 40.568 36.563 38.544 21.053
960
0.399 1.988 40.944 36.362 69.649 67.851 40.759 36.794 38.792 21.166
1080
0.399 2.064 41.196 36.561 69.602 68.072 40.939 36.972 38.980 21.211
1200
0.330 2.083 41.331 36.781 69.601 68.146 41.225 37.216 39.210 21.049

Energy Systems Lab 15
 Table 2: Adjusting the flow rate
Time,sec Pressure Flow
rate
Panel Reserv
oir
Glass
Upper
Glass
Lower
Air
Space
Water
in
Water
out
Am
nt
Units kPa l/min °C °C °C °C °C °C °C °C
0000 0.4142 0.998 41.926 37.158 69.759 68.363 41.703 37.488 40.658 21.1
120
34.357 0.976 42.396 37.434 69.778 68.514 42.022 37.756 40.916 21.3
240
34.603 0.999 42.711 37.603 69.785 68.534 42.342 37.932 41.084 21.1
360
34.576 1.024 42.862 37.803 69.871 68.596 42.541 38.221 41.330 20.9
480
34.132 1.029 43.124 38.062 69.976 68.747 42.773 38.434 41.523 21.0
600
34.697 1.018 43.346 38.285 70.266 68.929 42.987 38.600 41.814 21.2
720
35.781 1.028 43.600 38.523 70.395 69.014 43.209 38.876 41.950 21.2
840
35.440 0.998 43.355 38.678 70.055 68.954 43.242 39.047 41.905 21.2
960
35.648 0.984 43.301 38.846 70.237 68.994 43.267 39.206 42.023 21.5
1080
35.441 0.970 43.422 39.009 70.417 69.079 43.358 39.291 42.149 21.5
1200
0.414 0.998 41.926 37.158 69.759 68.363 41.703 37.488 40.658 21.1
 calculations
Basic formulas
Section Formula
Sola panel
Cover
Temperatur
e rise
Heat
transferred
from the
panel to the

Energy Systems Lab 16
cover
Convective
heat loss
from cover
 Available constants
ag = 0.1, aw = 0.9, tg = 0.8, εw = 0.96, hga = 10KJ/Kmh, λ. infrared = 10.5 μm, λ. optical = 0.5 μm,
m = 0.04
where
qwtr
the heat transferred to the water to give the temperature rise across the panel,
t g - transmissivity of the cover
 w - the absorptivity of the panel and the material,
Qb - the conduction heat loss from the base,
Cm * ẟ Tm
ẟ T - thermal lag term for unsteady operation
Tm - the mean material temperature
m - is the mass flow rate of the water over the solar panel in kg / s
 Determination of the cover section
From agQ + qrwg = qcga + qrga
q rwg = h rwg (Tw - Tg)
= εw σ (Tw4 – Tg4)
Taking σ = 56.69 * 10 KJ/m2K4
Determination of the solar plate

Energy Systems Lab 17
aw = 0.9, tg = 0.8,
awtg Q = qwtr + qb + Cm * ẟ Tm
ẟ T
qwtr = m Cw * (Tw 0−Tw 1)
 m cw Twoi
Taking Cw = 4.19
Tw 0,1 = Tw 1 - Tw 0,
Replacing Tw 0 and Tw1
Tw 0,1 = 25.498 – 23.353
= 2.145
qwtr = 0.04 * 4.19 * 2.145
= 0.3595
From the steam table; qwtr (120)
= 32.35 KJ/Kg
Qb = hb (Tw -Ta)
But hb = 1 / ( 1
h .bo + 1
k ¿
;therefore hb = 33 KJ/m2hk
Tw = 30.7 0C
Ta = 197 0C
(Tw –Ta) hb = qb
qb = 33 * 11

Energy Systems Lab 18
= 363 KJ/Km2h
Q max = 3.288 KJ/m2h
And ϑ = 17.50
Hence
Q max = 3.288 cos 17.50
= 3.136 KJ/m2h
Determination of efficiency
η = Q wtr
Q
Replacing, we obtain
η = 0.3595
3.136
= 11.46%
Theoretical efficiency
qwtr = awtg Q - qb - Cm * ẟ Tm
ẟ T
= 0.9 * 0.8* 3.136– 363 – 0 (Cm * ẟ Tm
ẟ T is very small thus assumed 0)
= -1. 30
η = 1.30
3.136
= 41.5 %
Using an insulation materials
Assuming thickness of 3 cm
hb = 1 / ( 1
h .bo + 1
k ¿

Energy Systems Lab 19
replacing
hb = 1 / ( 1
33 + 0.03
0 ¿
hb = 32.289
Qb = hb (Tw -Ta)
Replacing; we obtain
Qb = 32.289 (41.22 -21.22)
Qb = 652
qwtr = awtg Q - qb - Cm * ẟ Tm
ẟ T
replacing :
qwtr = 0.9 * 0.8 * 3.136– 0.652 - 0 (Cm * ẟ Tm
ẟ T is very small thus assumed 0)
= - 1.715
η = 1.715
3.136
= 54.7 %
Discussion
As it is seen from the above calculations, the addition of the solar plate increased the
effieicnecy of the plate, from 41.5 % to 54.7 %.
Experimental results relating to theory: In the relation of the results, which were obtained to the
theoretical results, a slight difference was noticed. The difference can be attributed to a number
of factors which have an influence on the collection of solar energy through an apparatus. These
factors include the incidence angle of solar radiation, the internal resistance of the various
equipment’s used in the experiment, the angle of the solar plate as well as other factors. One

Energy Systems Lab 20
factor also which is poised to affect the overall outcome is the human error during assembling of
the apparatuses. However, when these factors can be properly changed, it becomes possible to
determine the desired output.
One way to efficiently and efficiently capture solar energy is through maintaining the
solar plates at a particular position and angle. Various structures can be utilized for the purposes
of solar energy collection, storage as well as distribution in the form of heat. For the passive
solar buildings, they have the ability to maximize the solar energy absorption via the use of dark
colored, dense materials which are positioned southwards. These dense materials act as thermal
mass, by capturing and retaining the solar energy
Conclusions:
The use of solar panels in capturing and storing energy is one of the ways that can be
utilized in meeting the increasing demands of energy in the contemporary world. This
experiment has enabled us to have a clear understanding of how solar energy efficiency as well
as how the harnessing of solar energy through solar panels is conducted. Despite a variation
between the experimental and theoretical results, there are a number of factors which when
avoided, and then optimum efficiency can be achieved.

Energy Systems Lab 21
References
Alstone, P., Gershenson, D. and Kammen, D.M., 2015. Decentralized energy systems for clean
electricity access. Nature Climate Change, 5(4), pp.305-314.
Bahramara, S., Moghaddam, M.P. and Haghifam, M.R., 2016. Optimal planning of hybrid
renewable energy systems using HOMER: A review. Renewable and Sustainable Energy
Reviews, 62, pp.609-620.
Costa, S.C., Diniz, A.S.A. and Kazmerski, L.L., 2016. Dust and soiling issues and impacts
relating to solar energy systems: Literature review update for 2012–2015. Renewable and
Sustainable Energy Reviews, 63, pp.33-61.
Green, M.A., Emery, K., Hishikawa, Y., Warta, W. and Dunlop, E.D., 2015. Solar cell efficiency
tables (Version 45). Progress in photovoltaics: research and applications, 23(1), pp.1-9.
Harish, V.S.K.V. and Kumar, A., 2016. A review on modeling and simulation of building energy
systems. Renewable and sustainable energy reviews, 56, pp.1272-1292.
Ohta, T. ed., 2013. Solar-hydrogen energy systems: an authoritative review of water-splitting
systems by solar beam and solar heat: hydrogen production, storage and utilisation. Elsevier.
Pfenninger, S., Hawkes, A. and Keirstead, J., 2014. Energy systems modeling for twenty-first
century energy challenges. Renewable and Sustainable Energy Reviews, 33, pp.74-86.
Sinha, S. and Chandel, S.S., 2014. Review of software tools for hybrid renewable energy
systems. Renewable and Sustainable Energy Reviews, 32, pp.192-205.