Engineering and Computing

Desklib offers study material, solved assignments, essays, dissertations, and more on Engineering and Computing. Find expert help for your assignments and projects.

Running head: ENGINEERING AND COMPUTING
ENGINEERING AND COMPUTING
Name of the Student
Name of the University
Author Note

1ENGINEERING AND COMPUTING
Question 1:
MATLAB script:
clc
clear
disp('Question No 1: Your Name,Spring,2019')
x=-2*pi:0.1:2*pi;
y1 = sinh(x);
y2 = (exp(x) - exp(-x))/2;
plot(x,y1,'r-',x,y2,'b*')
legend('y1','y2')
title('Plot of sinh(x) and (e^{x} - e^{-x})/2')
xlabel('x in range -2\pi to 2\pi')
ylabel('y1 and y2')
Plot:

2ENGINEERING AND COMPUTING
-8 -6 -4 -2 0 2 4 6 8
x in range -2 to 2
-300
-200
-100
0
100
200
300
y1 and y2
Plot of sinh(x) and (ex - e-x)/2
y1
y2
Question 2:
The circuit is given below
Here, V = 10 volts, R1 = 100 Ω, R2 = 200 Ω, R3 = 300 Ω.

3ENGINEERING AND COMPUTING
Now, current i1 = V/Req
Here, Req = R1 + (R2*R3)/(R2 + R3) = 100 + (200*300)/500 = 100 + 120 = 220 Ω.
Hence, i1 = 10/220 = 0.0455 Amps.
Hence, i2 = 0.0455*R3/(R2+R3) = 0.0455*300/(500) = 0.0273 Amps.
Now, i3 = 0.0455*R2/(R2+R3) = 0.0455*200/(500) = 0.0182 Amps.
MATLAB script and output:
clc
clear
disp('Question No 2: Your Name,Spring,2019')
v = 10; r1 = 100; r2 = 200; r3 = 300;
req = r1 + (r2*r3)/(r2 + r3);
i1 = v/req
i2 = i1*r3/(r2+r3)
i3 = i1*r2/(r2+r3)
Question No 2: Your Name,Spring,2019
i1 =
0.0455
i2 =
0.0273
i3 =

4ENGINEERING AND COMPUTING
0.0182
Question 3:
The equation of the quadratic polynomial is y = a x2 +bx+ c
The curve passes through points (-16,38), (5,9) and (25,32). Hence, putting the boundary
conditions in equation we get,
38 = a*256 -16b + c
9 = 25a + 5b + c
32 = 625a + 25b + c
Now, solving these matrix inversion method.
[256 −16 1
25 5 1
625 25 1 ][a
b
c ]= [38
9
32 ]
MATLAB script and output:
A = [256 -16 1;25 5 1;625 25 1];
>> B = [38;9;32];
>> sol = linsolve(A,B)
sol =
0.0617
-0.7019
10.9663
Hence, a = 0.0617, b = -0.7019 and c = 10.9663.

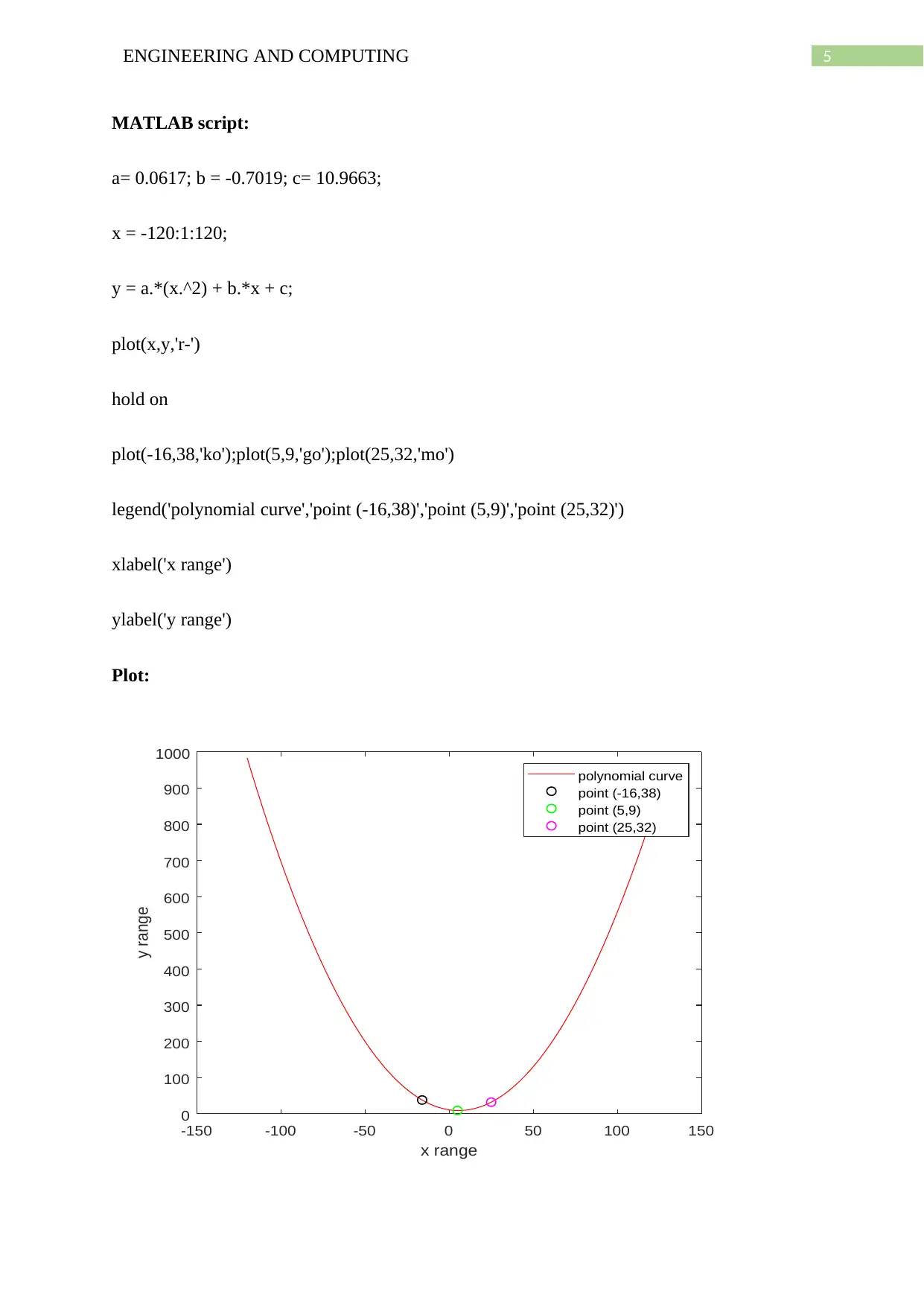
5ENGINEERING AND COMPUTING
MATLAB script:
a= 0.0617; b = -0.7019; c= 10.9663;
x = -120:1:120;
y = a.*(x.^2) + b.*x + c;
plot(x,y,'r-')
hold on
plot(-16,38,'ko');plot(5,9,'go');plot(25,32,'mo')
legend('polynomial curve','point (-16,38)','point (5,9)','point (25,32)')
xlabel('x range')
ylabel('y range')
Plot:
-150 -100 -50 0 50 100 150
x range
0
100
200
300
400
500
600
700
800
900
1000
y range
polynomial curve
point (-16,38)
point (5,9)
point (25,32)

6ENGINEERING AND COMPUTING
Question 4:
y’ = (sin(t))^2, y(0) = 0.
Range of t = 0 to 10, h = 0.1 is considered or t = 0, 0.1, 0.2….10.
MATLAB function:
clc
clear
disp('Question No 4: Your Name,Spring,2019')
f = @(t,y)(sin(t)^2);
y(1) = 0;h=0.1;
t = 0:0.1:10;
for i=1:length(t)
y(i+1) = y(i) + h*f(t(i),y(i));
end
plot(t,y(1:end-1),'r*')
title('Solution of dy\dt = (sin(t))^2 by Euler method')
xlabel('time t')
ylabel('solution y(t)')
Plot:

7ENGINEERING AND COMPUTING
0 1 2 3 4 5 6 7 8 9 10
time t
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
solution y(t)
Solution of dy\dt = (sin(t))^2 by Euler method
Question 5:
Given, the mass of the object is m = 100 kg.
F=500 ( 2 – 5∗e−t )
Now, acceleration of the object is given by Newton’s law
F = ma => a = F/m = 500 ( 2 – 5∗e−t ) /100 = 5 ( 2−5 e−t )
Now, the velocity of the object is found by integrating the acceleration by trapezoidal
method. Also, the mass is at rest at t = 0 or v(0) = 0.
Step size h = 0.1.

8ENGINEERING AND COMPUTING
MATLAB code:
clc
clear
disp('Question No 5: Your Name,Spring,2019')
h=0.1;
a = @(t) (5*(2-5*exp(t)));
t= 0:h:5;
for i =1:(length(t)-1)
v(i+1) = (h/2)*(a(t(i)) + a(t(i+1)));
acc(i) = a(t(i));
end
plot(t,v,'r*',t(1:(end-1)),acc,'b*')
legend('v(t)','a(t)')
title('Plot of velocity and accleration as a function of time')
xlabel('time t in 0 to 5 sec')
ylabel('v(t) and a(t)')
Plot of velocity and acceleration w.r.t time:

9ENGINEERING AND COMPUTING
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
time t in 0 to 5 sec
-3500
-3000
-2500
-2000
-1500
-1000
-500
0
v(t) and a(t)
Plot of velocity and accleration as a function of time
v(t)
a(t)
Question 6:
The given differential equation is
3 ¨y +3 ˙y +75 y=10 sin(5 t )
Initial conditions
y(0) = 3 and ˙y ( 0 )=6.
2nd order differential equation are broken down two first order differential equation.
˙y=a
3 ˙a+3 a+75 y=10 sin (5 t ) => ˙a = (10 sin ( 5 t ) −3 a−75 y )/3

10ENGINEERING AND COMPUTING
MATLAB function:
clc
clear
disp('Question No 6: Your Name,Spring,2019')
h = 0.1;
dy = @(t,a) (a);
d2y = @(a,t,y) (10*sin(5*t) - 3*a - 75*y)/3;
a(1) = 6; y(1) = 3;
t = 0:0.1:10;
for i=1:length(t)
y(i+1) = y(i) + h*dy(t(i),a(i));
a(i+1) = a(i) + h*d2y(a(i),t(i),y(i));
end
plot(t,a(1:end-1),'r-',t,y(1:end-1),'b-')
legend('dy/dt','y')
xlabel('time t')
ylabel('dy/dt and y')

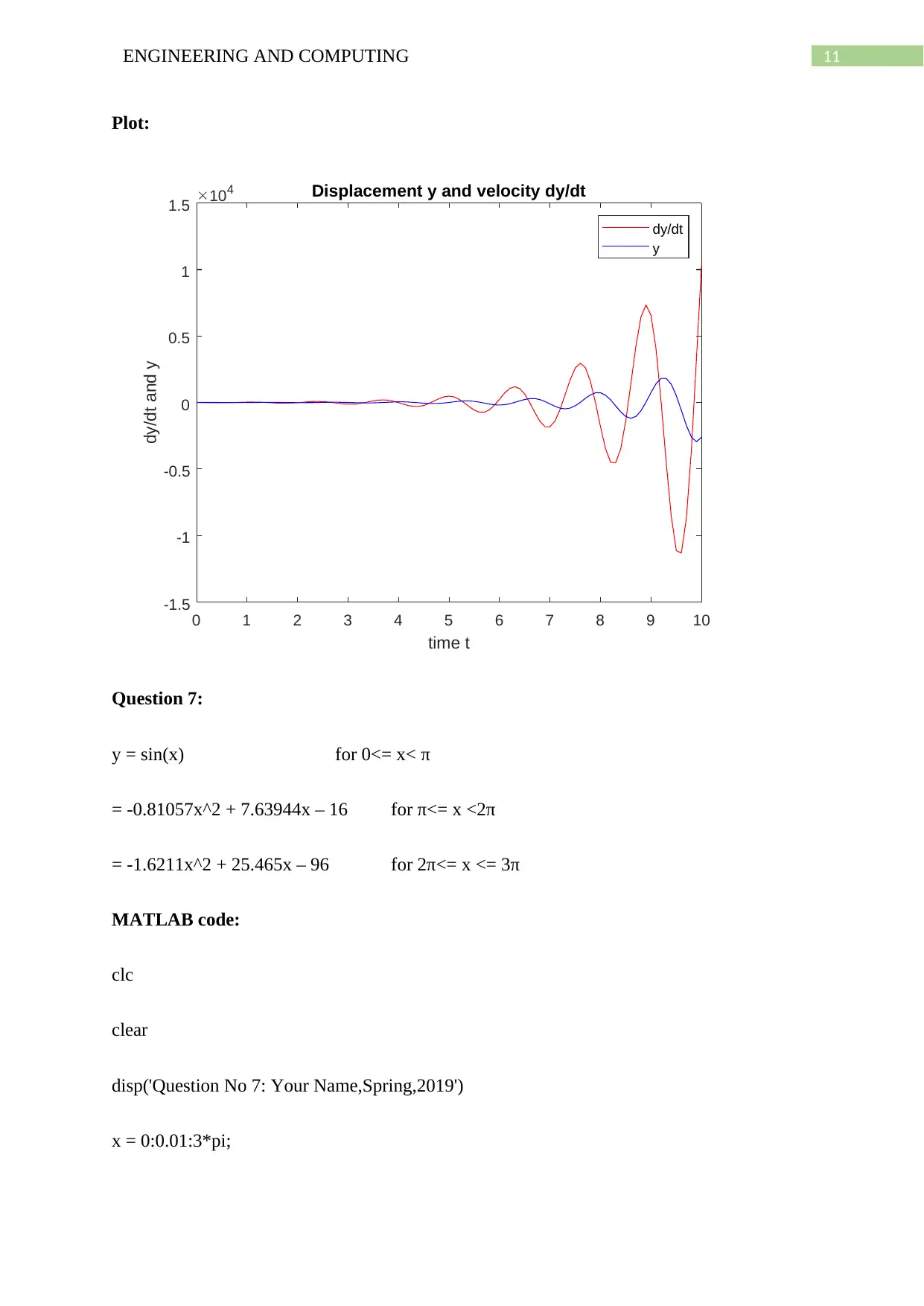
11ENGINEERING AND COMPUTING
Plot:
0 1 2 3 4 5 6 7 8 9 10
time t
-1.5
-1
-0.5
0
0.5
1
1.5
dy/dt and y
104 Displacement y and velocity dy/dt
dy/dt
y
Question 7:
y = sin(x) for 0<= x< π
= -0.81057x^2 + 7.63944x – 16 for π<= x <2π
= -1.6211x^2 + 25.465x – 96 for 2π<= x <= 3π
MATLAB code:
clc
clear
disp('Question No 7: Your Name,Spring,2019')
x = 0:0.01:3*pi;

12ENGINEERING AND COMPUTING
i=1;
while i<=length(x)
if x(i) < pi
y(i) = sin(x(i));
elseif x(i)<2*pi && x(i)>= pi
y(i) = -0.81057*(x(i))^2 + 7.63944*x(i) - 16;
else
y(i) = -1.6211*(x(i))^2 + 25.465*x(i) - 96;
end
i = i+1;
end
plot(x,y,'m*')
xlabel('x range')
ylabel('y value')
title('y vs x')
Plot:

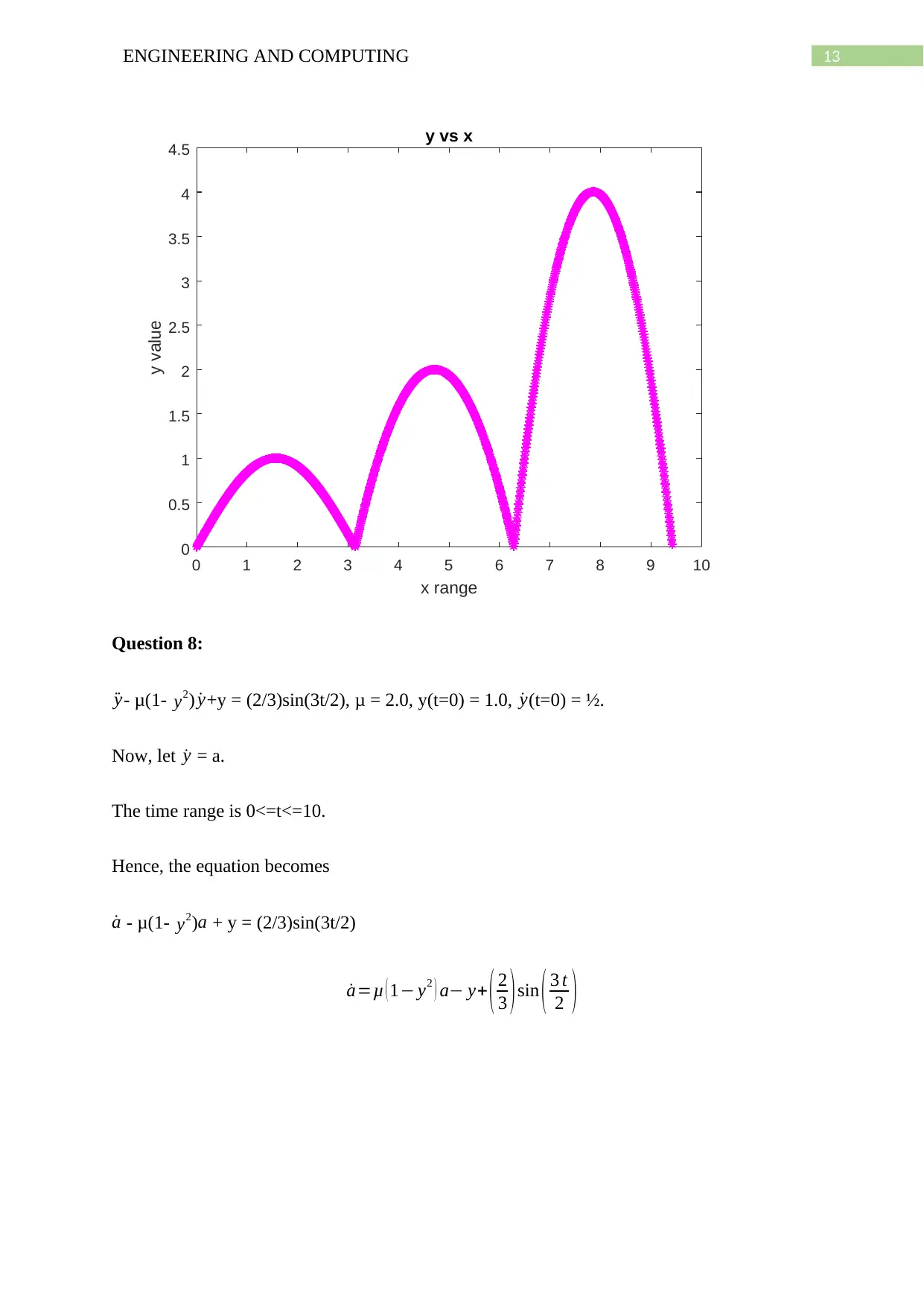
13ENGINEERING AND COMPUTING
0 1 2 3 4 5 6 7 8 9 10
x range
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
y value
y vs x
Question 8:
¨y- μ(1- y2) ˙y+y = (2/3)sin(3t/2), μ = 2.0, y(t=0) = 1.0, ˙y(t=0) = ½.
Now, let ˙y = a.
The time range is 0<=t<=10.
Hence, the equation becomes
˙a - μ(1- y2)a + y = (2/3)sin(3t/2)
˙a=μ ( 1− y2 ) a− y+ ( 2
3 ) sin ( 3 t
2 )

14ENGINEERING AND COMPUTING
MATLAB code:
clc
clear
disp('Question No 8: Your Name,Spring,2019')
h = 0.1; miu = 2;
dy = @(t,a) (a);
d2y = @(a,t,y) (miu*(1-y^2)*a - y + (2/3)*sin(3*t/2));
a(1) = (1/2); y(1) = 1;
t = 0:0.1:10;
for i=1:length(t)
y(i+1) = y(i) + h*dy(t(i),a(i));
a(i+1) = a(i) + h*d2y(a(i),t(i),y(i));
end
plot(t,a(1:end-1),'r-',t,y(1:end-1),'b-')
legend('dy/dt','y(t)')
xlabel('time t in secs')
ylabel('dy/dt and y')
title('solution y(t) and dy/dt')

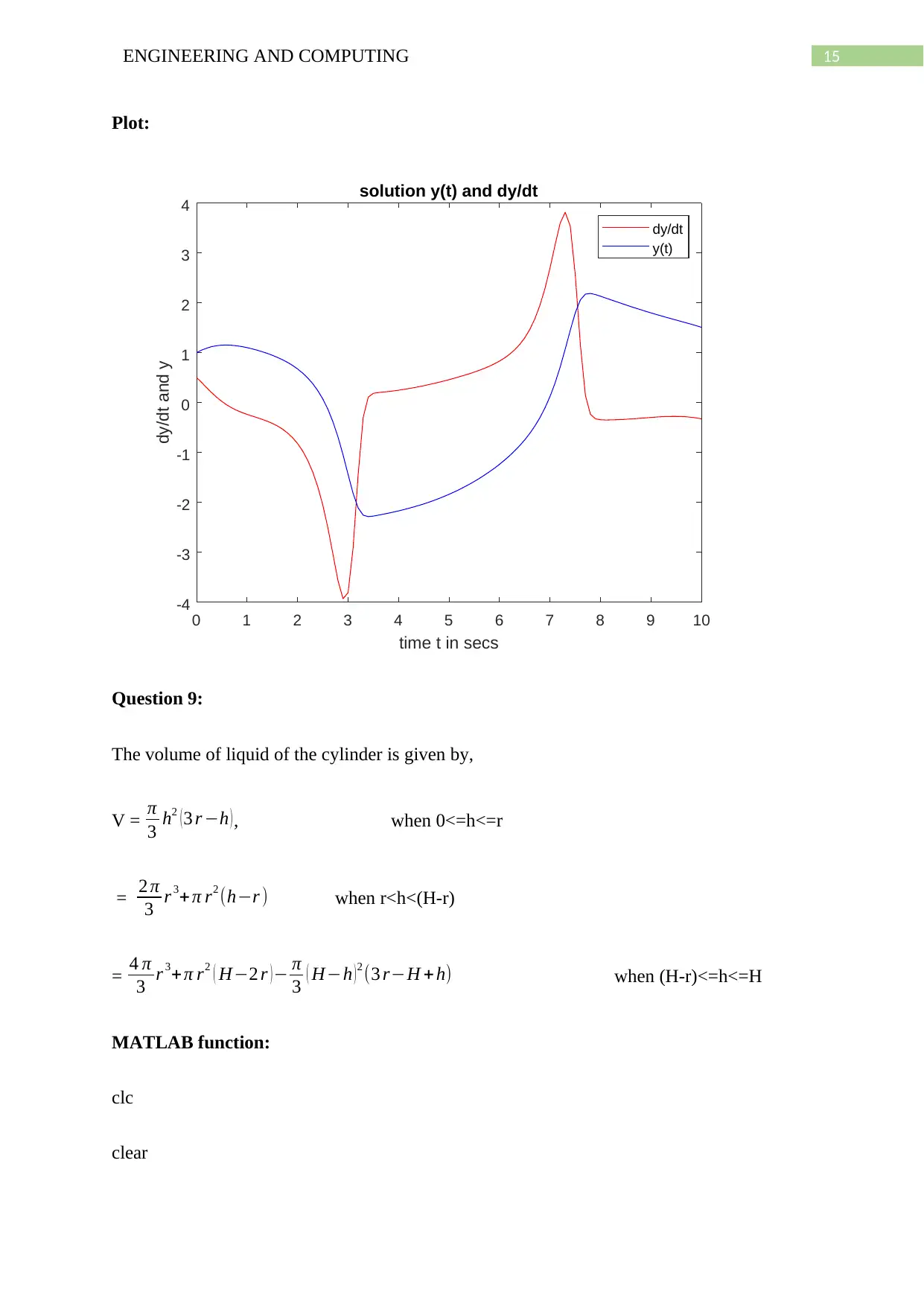
15ENGINEERING AND COMPUTING
Plot:
0 1 2 3 4 5 6 7 8 9 10
time t in secs
-4
-3
-2
-1
0
1
2
3
4
dy/dt and y
solution y(t) and dy/dt
dy/dt
y(t)
Question 9:
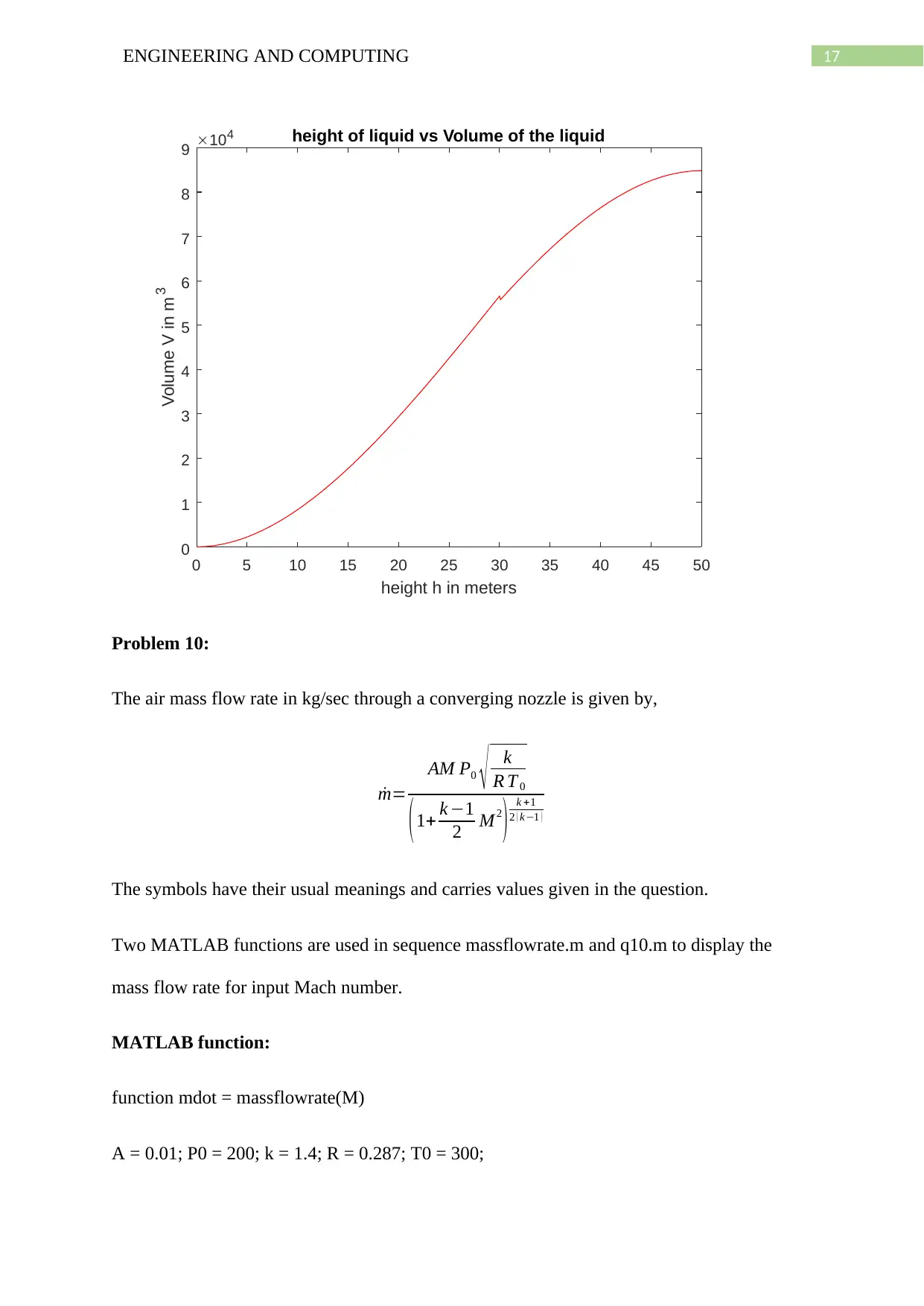
The volume of liquid of the cylinder is given by,
V = π
3 h2 (3 r −h ), when 0<=h<=r
= 2 π
3 r 3+ π r2 (h−r ) when r<h<(H-r)
= 4 π
3 r 3+π r2 ( H−2 r ) − π
3 ( H−h ) 2 (3 r−H + h) when (H-r)<=h<=H
MATLAB function:
clc
clear

16ENGINEERING AND COMPUTING
disp('Question No 9: Your Name,Spring,2019')
r = 30; H = 50;
h = 0:0.1:50; i=1;
while i <= length(h)
if h(i)<=r
V(i) = (pi/3)*(h(i)^2)*(3*r - h(i));
elseif h(i)>r && h(i)<(H-r)
V(i) = (2*pi/3)*(r^3) + pi*(r^2)*(h(i) - r);
else
V(i) = (4*pi/3)*(r^3) + pi*(r^2)*(H-2*r) - (pi/3)*((H-h(i))^2)*(3*r - H+ h(i));
end
i=i+1;
end
plot(h,V,'r-')
xlabel('height h in meters')
ylabel('Volume V in m^3')
title('height of liquid vs Volume of the liquid')
Plot:

17ENGINEERING AND COMPUTING
0 5 10 15 20 25 30 35 40 45 50
height h in meters
0
1
2
3
4
5
6
7
8
9
Volume V in m 3
104 height of liquid vs Volume of the liquid
Problem 10:
The air mass flow rate in kg/sec through a converging nozzle is given by,
˙m=
AM P0 √ k
R T 0
(1+ k −1
2 M2
) k +1
2 ( k−1 )
The symbols have their usual meanings and carries values given in the question.
Two MATLAB functions are used in sequence massflowrate.m and q10.m to display the
mass flow rate for input Mach number.
MATLAB function:
function mdot = massflowrate(M)
A = 0.01; P0 = 200; k = 1.4; R = 0.287; T0 = 300;

18ENGINEERING AND COMPUTING
mdot = (A*M*P0*sqrt((k/R*T0)))/((1+ (k-1)*(M^2)/2)^(k+1)/(2*(k-1)));
sprintf('When the Mach number of air flow is %f then the mass flow rate is %f
kg/sec',M,mdot)
end
clc
clear
disp('Question No 10: Your Name,Spring,2019')
M = input('Enter Mach number M \n');
format short
mdot = massflowrate(M);
Output:
Question No 10: Your Name,Spring,2019
Enter Mach number M
2
ans =
'When the Mach number of air flow is 2.000000 then the mass flow rate is 29.866179
kg/sec'