Engineering Math Assignment: Cable Optimization & Channel Design

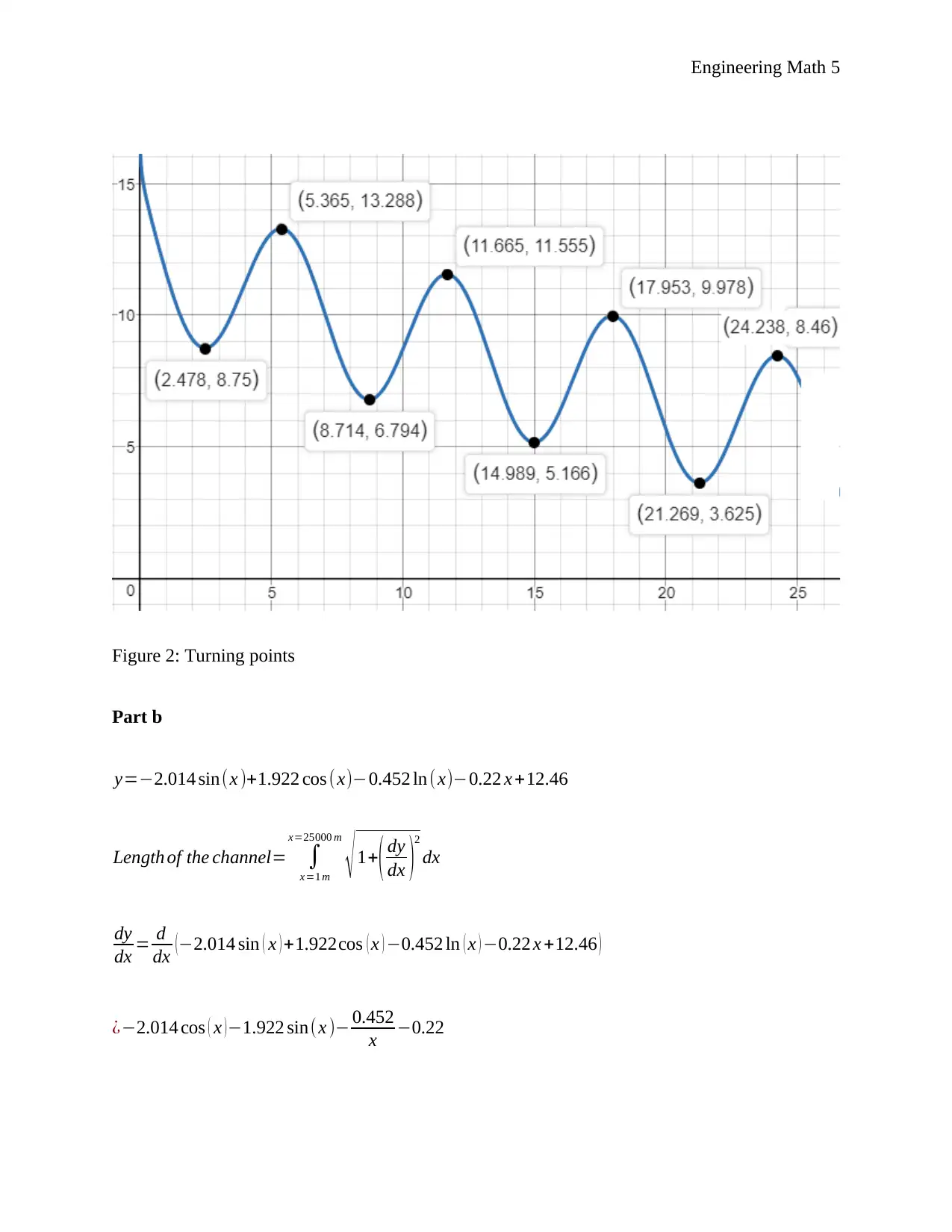
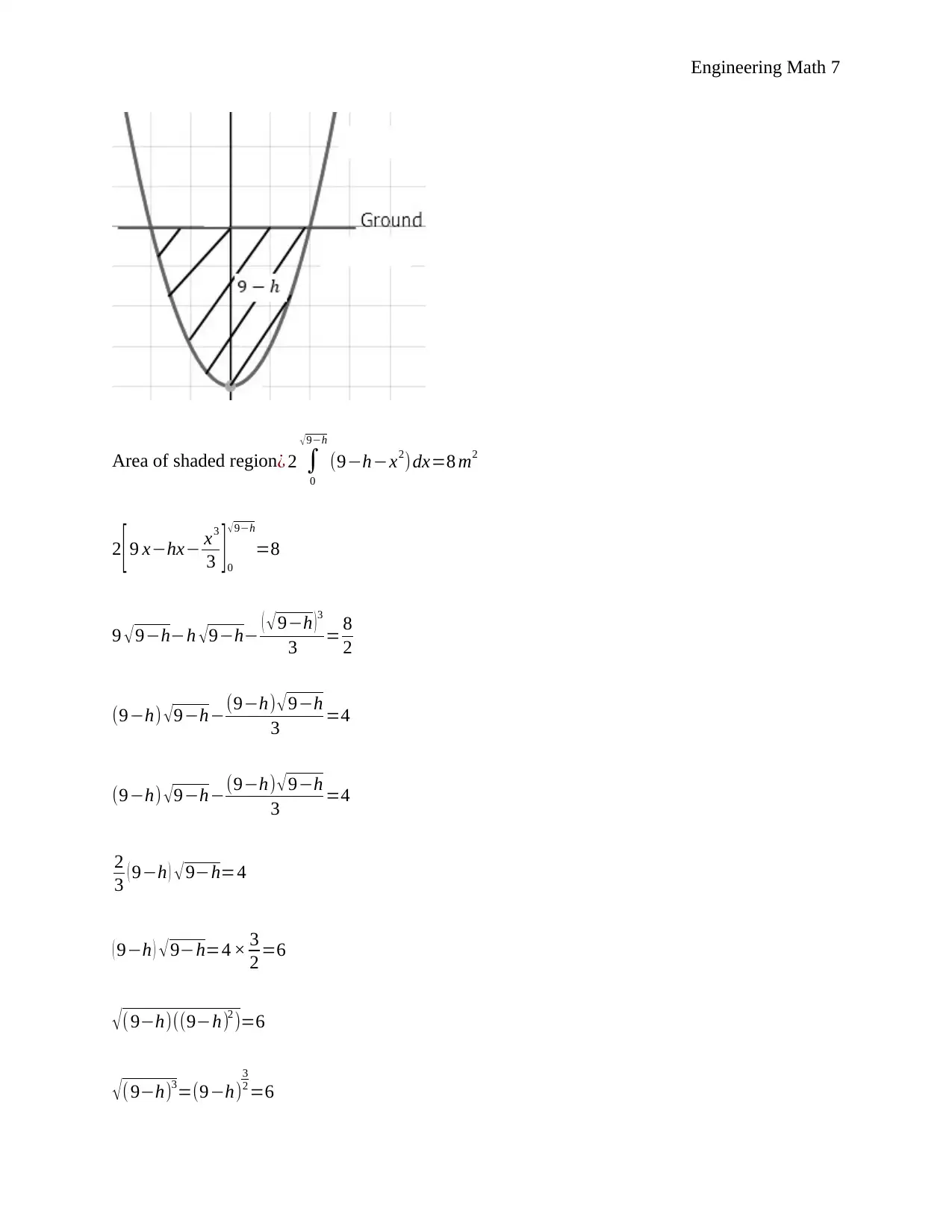
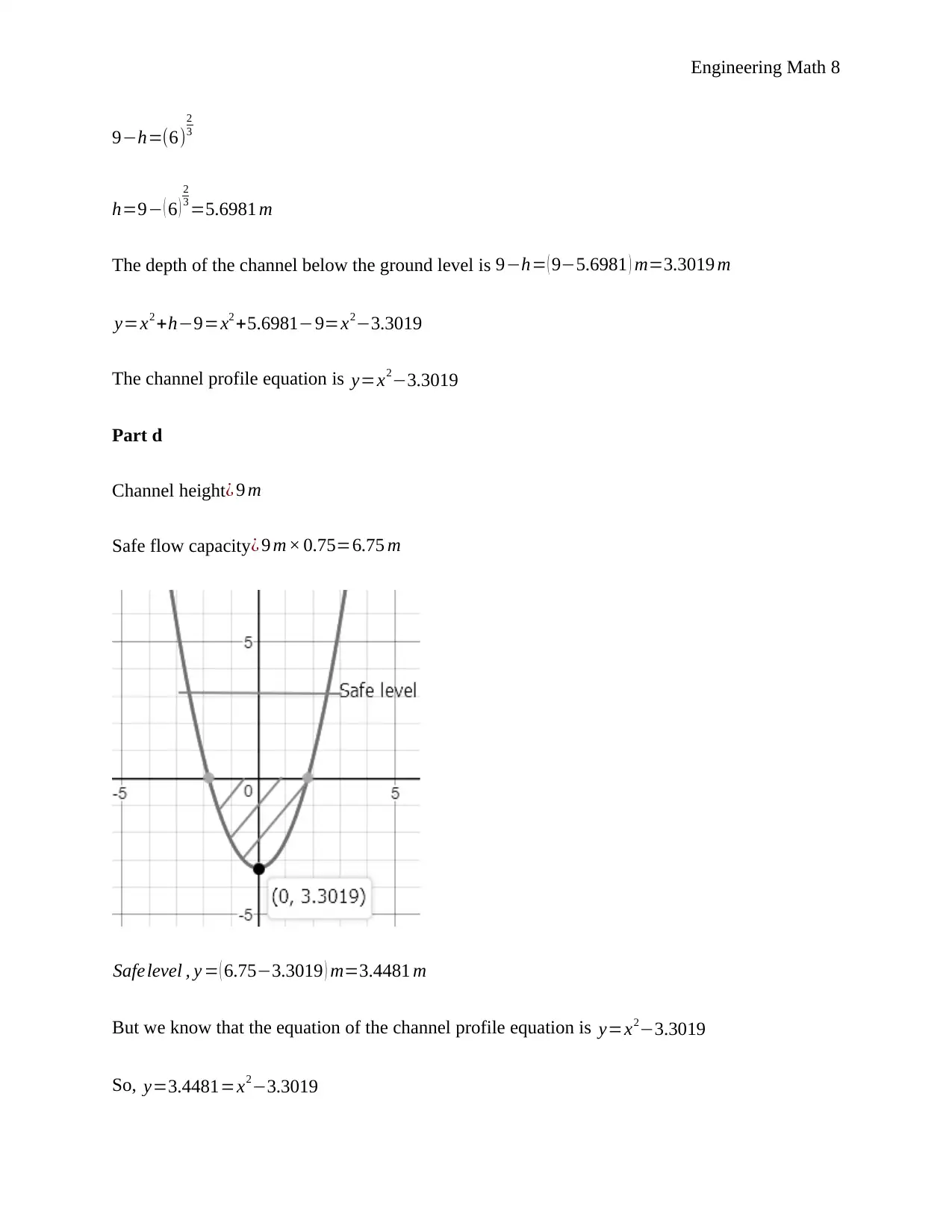
This engineering mathematics assignment solution addresses two primary problems: optimizing cable length and analyzing a channel profile. The first problem involves determining the minimum cost of laying a cable connecting an island to an exchange, considering both underwater and land routes. Calculus is used to find the optimal distance 'x' that minimizes the total cost. The second problem analyzes a channel profile, using Desmos to plot turning points and integral calculus to calculate the channel's length. It further explores the channel's geometry, determining the depth and safe flow capacity, and estimating the cost of lining material based on area calculations. The solution demonstrates a comprehensive application of mathematical principles to solve practical engineering problems.

Engineering Math 1
Engineering Math
Student’s Name
Course
Professor’s Name
University
City (State)
Date

Engineering Math 2
Engineering Math
Question 1
Part a
Figure 1: Cable Laying
To connect the island to the nearest exchange, we need to calculate the length of the cable
required. Then, using the costs of the cable per unit length, we can get the total cost.
The distance AE=(42−x ) km
Then, we can see that AI is the hypotenuse of triangle IPA. applying the Pythagoras Theorem,
AI2=252+ x2=625+ x2
AI is the distance under water hence, the length of the cable under water ¿ AI= √ 625+ x2 km
Hence, the cost of the cable under water ¿ $ 3600× √ 625+ x2=$ 3600 √ 625+ x2
AE is the distance on land. As a result, the length of the cable on land¿ ( 42−x ) km
Hence, the cost of the cable on land ¿ $ 2700× ( 42−x )=$ 2700 ( 42−x )

Engineering Math 3
Total cost of cable=Cost of cable under water +Cost of cable on land
Total Cable cost , C=3600 √625+ x2+2700 ( 42−x )
Part b
For the cost of laying the cable to be minimum, dC
dx =0
We know that, C=3600 √625+ x2+2700 ( 42−x )
dC
dx = d
dx ( 3600 √ 625+x2 ) + d
dx ( 2700 ( 42−x ) )
¿ 3600 d
dx ( √625+ x2 ) +2700 d
dx ( 42−x )
Let 625+ x2=u so that d u
dx =2 x
√ 625+ x2= √ u=u
1
2
dC
du = 1
2 u
−1
2 = 1
2 √625+ x2
3600 dC
dx =3600 dC
du × du
dx =2 x 3600
2 √625+x2 = 3600 x
√625+ x2
2700 d
dx ( 42−x ) =2700 (−1 )=−2700
dC
dx = 3600 x
√625+ x2 −2700=0
3600 x
√625+ x2 =2700

Engineering Math 4
(3600 x)2=27002(625+ x2)
625+ x2= ( 3600 )2
27002 x2= 16
9 x2
16
9 x2−x2=625
7
9 x2=625 , x2=625 × 9
7 = 5625
7
x= √ 625 × 9
7 = √ 5625
7 = 75
√ 7 m
The cost of laying the cable is minimum when x= 75
√7 m
Minimum cost ¿ C ( 75
√ 7 )=$ ( 3600 √ 625+ 5625
7 +2700 ( 42− 75
√ 7 ) )
Minimum cost of the cable=$ 172,929.40
Question 2
Part a
As it can be seen, there are four maximum turning points as well as four minimum turning points
for the profile in the proposed channel. Given that,
y=−2.014 sinx +1.922cosx−0.452 lnx−0.22 x+ 12.46, the turning are shown in figure 2 using
Desmos. Desmos is a graphing calculator which we can use to plot the channel profile given the
relationship between y and x as shown in figure 2.

Engineering Math 5
Figure 2: Turning points
Part b
y=−2.014 sin(x )+1.922 cos (x)−0.452 ln( x)−0.22 x +12.46
Length of the channel= ∫
x=1 m
x=25000 m
√ 1+( dy
dx )
2
dx
dy
dx = d
dx (−2.014 sin ( x ) +1.922cos ( x ) −0.452 ln ( x ) −0.22 x +12.46 )
¿−2.014 cos ( x )−1.922 sin(x )− 0.452
x −0.22

Engineering Math 6
¿ dy
dx ∨¿ 2.014 cos ( x ) +1.922sin ( x ) + 0.452
x +0.22
Channel length= ∫
x=1
x=25 000
√ 1+( 2.014 cos ( x )+1.922sin ( x ) + 0.452
x +0.22)
2
dx
Solving the equation above we obtain, Channel length=56960.1m
Part c
Maximum channel width ¿ 6 m
Minimum cross section area ¿ 8 m2
The x-intercepts are x=−3∧, x=3
Which implies that x +3=0∧, x−3=0
Then, y= ( x +3 ) ( x−3 )=x2−9
Let the depth of the channel be 9−h
The equation of the shaded region is:
−h− ( x2−9 ) =9−h−x2
The curve y=x2−9 and the line y=−h meet at:
y=x2−9=−h
x2−9=−h
x2=9−h
x=± √ 9−h

Engineering Math 7
Area of shaded region ¿ 2 ∫
0
√ 9−h
(9−h−x2)dx=8 m2
2 [9 x−hx− x3
3 ]0
√9−h
=8
9 √ 9−h−h √ 9−h− ( √ 9−h ) 3
3 = 8
2
(9−h) √ 9−h−(9−h) √ 9−h
3 =4
(9−h) √ 9−h−(9−h) √ 9−h
3 =4
2
3 ( 9−h ) √ 9−h=4
( 9−h ) √9−h=4 × 3
2 =6
√ (9−h)((9−h)2 )=6
√( 9−h)3=(9−h)
3
2 =6

Engineering Math 8
9−h=(6)
2
3
h=9− ( 6 )
2
3 =5.6981 m
The depth of the channel below the ground level is 9−h= ( 9−5.6981 ) m=3.3019 m
y=x2 +h−9=x2 +5.6981−9=x2−3.3019
The channel profile equation is y=x2−3.3019
Part d
Channel height¿ 9 m
Safe flow capacity ¿ 9 m× 0.75=6.75 m
Safelevel , y = ( 6.75−3.3019 ) m=3.4481 m
But we know that the equation of the channel profile equation is y=x2−3.3019
So, y=3.4481=x2−3.3019

Engineering Math 9
x2=3.4481+3.3019=6.75
x= √6.75=±2.598 1
Maximum safe area ¿ 2 ∫
0
2.598
¿ ¿
¿ ∫
−2.5981
2.598 1
(6.75−x2) dx
¿ 2 [ 6.75 x− x3
3 ]−2.5981
2.598 1
=2 ( 6.75 ×2.598− 2.5983
3 )=23.3827 m2
Therefore, the maximum safe area is 23.3827 m2
Part e
The area of the channel up to the ground level represents the total area where the lining material
will be applied. That is, the difference between the safe area and the minimum cross-section of
the channel.
¿ ( 23.3827−8 ) m2=15.3827 m2
Cost of lining material Total area×Cost per unit area
Cost=15.3827 ×30=$ 461.4810