Engineering Mathematics 1

This document contains solved problems on Engineering Mathematics 1 including topics like differentiation, integration, optimization, and population growth. Each problem is solved step-by-step with explanations. The course code, course name, and university are not mentioned.

Engineering Mathematics 1
Engineering Mathematics
Student’s Name
Course
Professor’s Name
University
City (State)
Date

Engineering Mathematics 2
Engineering Mathematics
Question 1
Part a
y= 2 x4−3 x
4 x−1
dy
dx =
( 4 x−1 ) d
dx ( 2 x4 −3 x )− ( 2 x4−3 x ) d
dx ( 4 x−1 )
( 4 x−1)2
d
dx ( 4 x −1 )=4
d
dx (2 x4−3 x )=8 x3−3
dy
dx =(4 x−1)(8 x3−3)− ( 2 x4 −3 x ) 4
( 4 x−1)2 =¿ ¿
¿ −8 x4 +12 x +32 x4−12 x−8 x3+3
(4 x −1)2
¿ 24 x4−8 x3 +3
(4 x−1)2
Part b
y=6 cos ( x3 +3)
dy
dx =6 d
dx cos ( x3 +3)
Let x3+3=u so that y=6 cos u

Engineering Mathematics 3
dy
du =−6 sinu=−6 sin (x3+ 3)
du
dx = d
dx (x3 +3)=3 x2
dy
dx = dy
du × du
dx =−6 sin ( x3 +3 ) × 3 x2 =−18 x2 sin ( x3+3 )
dy
dx =−18 x2 sin ( x3+ 3 )
Part c
y= ( 4 x2−e2 x ) sin ( 3 x )
We apply the product rule, ( f . g ) '=f ' g+ f g'
f =4 x2−e2 x
f '= d
dx ( 4 x2 ) − d
dx ( e2 x ) =8 x−2 e2 x
g=sin ( 3 x )
g '= d
dx sin ( 3 x ) =3 cos (3 x)
dy
dx =f ' g+f g' = ( 8 x −2 e2 x ) sin ( 3 x )+ 3(4 x2−e2 x)cos (3 x )
Question 2
angular displacement ,θ=0.5 t4−t3
Part a

Engineering Mathematics 4
angular velocity= dθ
dt = d
dt ( 0.5 t4 −t3 )=4 ( 0.5 ) t3 −3 t2=2t3−3 t2
When t=2 , angular velocity=2( 2)3−3 ( 2 )2=16−12=4 rad s−1
Part b
angular acceleration= d2 θ
d t2 = d
dt ( 2 t3 −3 t2 ) =6 t2 −6 t
When t=3 , angular acceleration=6 ( 3 ) 2−6 ( 3 ) =36 rad s−2
Part c
angular acceleration=6 t2−6 t=0
t ( 6 t−6 )=0 , t=0∨6 t−6=0 , 6 t=6 ,t= 6
6 =1 s
Therefore, acceleration is zero when t=0∧when t =1 s
Question 3
Part a
The resulting rectangular sheet and open box are shown in figure 1 and figure 2.

Engineering Mathematics 5
Part b
Volume=9000 x−390 x2+4 x3
Volume=L× W × H=(120−2 x )(75−2 x)( x )
¿( 120−2 x)(75 x−2 x2)
¿ 120 ( 75 x−2 x2 ) −2 x (75 x−2 x2 )
¿ 9000 x−240 x2−150 x2 + 4 x3
V =9000 x −39 0 x2 +4 x3
Part c
Volume is maximum when dV
dx =0. That is,
dV
dx = d
dx ( 9000 x−390 x2+ 4 x3 )=0
d
dx ( 9000 x−390 x2+ 4 x3 )=9000−780 x+12 x2=0
Using the quadratic formula,
x= 780 ± √7802−4(12)(9000)
2(12) = 780± 420
24 =32.5± 17.5
x=32.5+17.5=50∨x=32.5−17.5=15
The width of the box is 75−2 x. When x=50, width equals 75−2 ( 50 )=−25 implying that
x=50 should be ignored. Therefore, the volume is maximum when x=15 mm

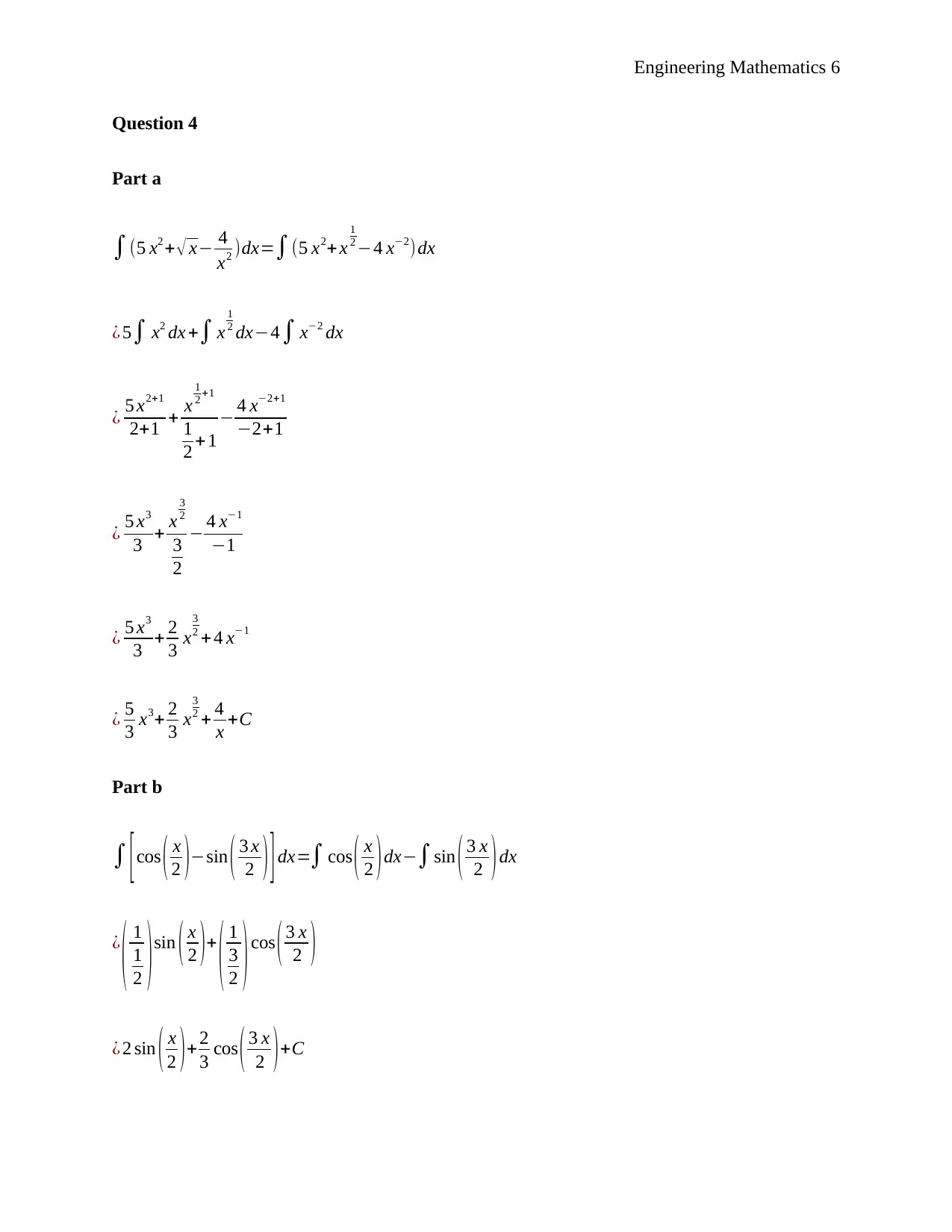
Engineering Mathematics 6
Question 4
Part a
∫(5 x2 + √ x− 4
x2 )dx=∫(5 x2+ x
1
2 −4 x−2)dx
¿ 5∫ x2 dx +∫ x
1
2 dx−4∫ x−2 dx
¿ 5 x2+1
2+1 + x
1
2 +1
1
2 + 1
− 4 x−2+1
−2+1
¿ 5 x3
3 + x
3
2
3
2
− 4 x−1
−1
¿ 5 x3
3 + 2
3 x
3
2 + 4 x−1
¿ 5
3 x3+ 2
3 x
3
2 + 4
x +C
Part b
∫ [cos ( x
2 )−sin ( 3 x
2 ) ] dx=∫ cos ( x
2 )dx−∫sin ( 3 x
2 )dx
¿
( 1
1
2 ) sin ( x
2 ) +
( 1
3
2 ) cos ( 3 x
2 )
¿ 2 sin ( x
2 )+ 2
3 cos ( 3 x
2 )+C

Engineering Mathematics 7
Part c
∫
1
5
s
√ s2+4 ds
¿ evaluating ,∫ s
√s2+ 4 ds welet s2 + 4=u so that,
du
ds =2 s , ds= du
2 s
∫ s
√ s2+ 4 ds=∫ s
√ u × du
2 s =∫ 1
2 √ u du=1
2 ∫ 1
√ u du= 1
2 ∫u
−1
2 du
¿ 1
2 ( 1
−1
2 +1 )u
−1
2 +1
= 1
2 ( 1
1
2 )u
1
2 =u
1
2 = √u= √s2 +4
∫
1
5
s
√ s2+4 ds=¿ √ s2 +4∨¿1
5 = √ 52+ 4− √ 12+ 4= √ 29− √ 5=3.149096 ¿
Question 5
Part a
y= 1
x , x=2∧x=6
The area bounded by the curve and the lines is shaded in the figure below.

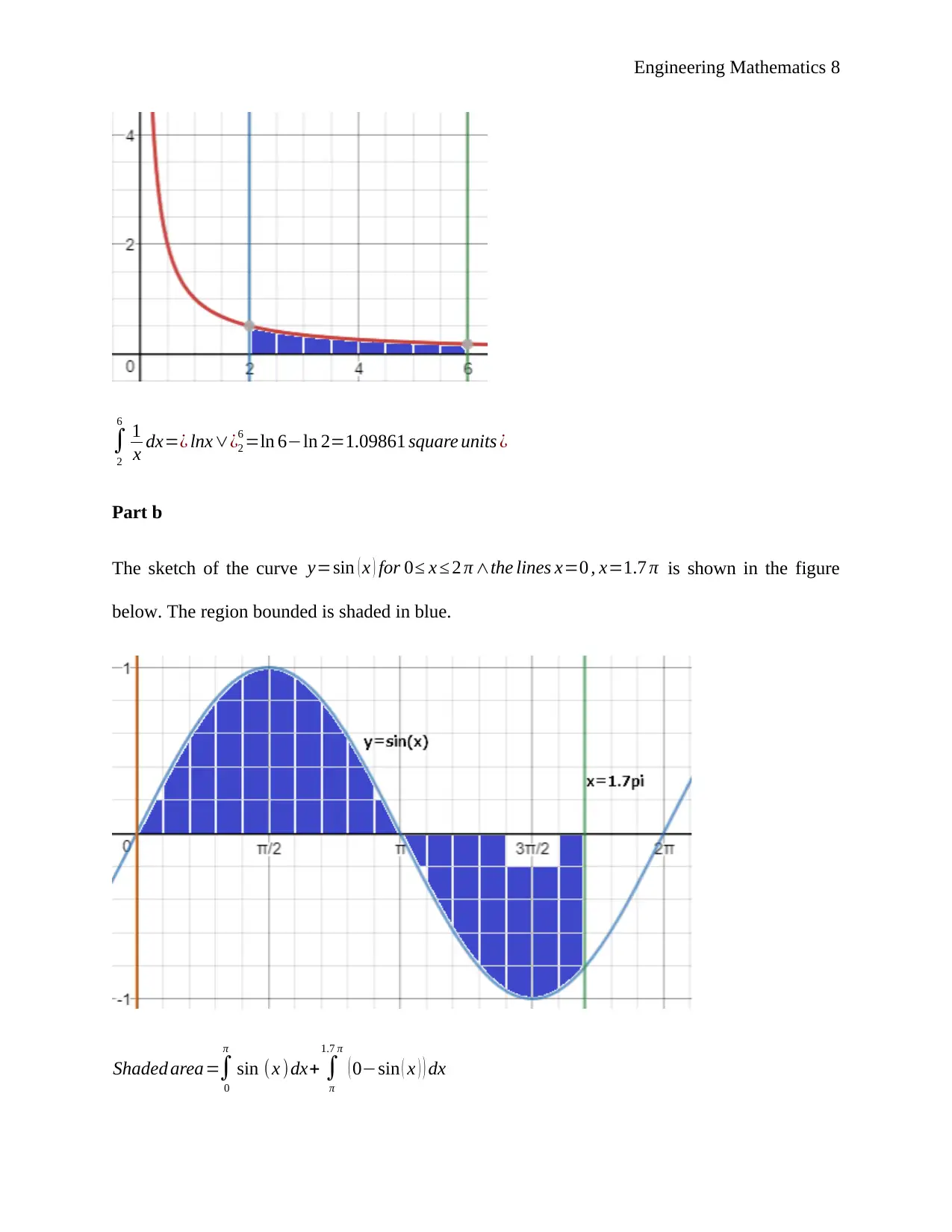
Engineering Mathematics 8
∫
2
6
1
x dx=¿ lnx∨¿2
6 =ln 6−ln 2=1.09861 square units ¿
Part b
The sketch of the curve y=sin ( x ) for 0≤ x ≤ 2 π ∧the lines x=0 , x=1.7 π is shown in the figure
below. The region bounded is shaded in blue.
Shaded area=∫
0
π
sin (x )dx+ ∫
π
1.7 π
( 0−sin ( x ) ) dx

Engineering Mathematics 9
¿∫
0
π
sin (x) dx− ∫
π
1.7 π
sin (x)dx
¿−¿ cos ( x )∨¿0
π −¿ ¿
¿−¿ cos ( x )∨¿0
π +¿ cos ( x )∨¿π
1.7 π ¿¿
¿−¿
¿−¿
¿ 2+0.5878+1=3.5878
Therefore, area ¿ 3.5878 square units
Question 6
Part a
Population per year=50 t2−100 t
3
2
Population after t years=∫(50t2−100 t
3
2 )dt=50 t3
3 −100 t
5
2
5
2
+C
¿ 50
3 t3−4 0 t
5
2 +C
Initial population P ( 0 )=C=25000
Therefore , thetotal population after t years=50
3 t3 −40 t
5
2 + 25000
Part b

Engineering Mathematics 10
Population after 25 years=50
3 ( 25 )3−40 ( 25 )
5
2 +25000
¿ 781250
3 −40(3125)+2500 0
¿ 260416.7−125000+ 2500 0
¿ 160416.7 ≅ 160417 people
Question 7
∫5 xcos ( 4 x ) dx=5∫ xcos ( 4 x ) dx
Let x=u , du=dx∧dv=cos (4 x ) so that,
v=∫ c os (4 x )dx= 1
4 sin (4 x)
∫ xcos ( 4 x ) dx=∫udv=uv−∫ vdu
uv−∫ vdu= x
4 sin ( 4 x ) −∫ 1
4 sin ( 4 x ) dx= x
4 sin ( 4 x ) + 1
16 cos (4 x )
∫5 xcos ( 4 x ) dx=5 ( x
4 sin ( 4 x )+ 1
16 cos ( 4 x ) )+C
¿ 5
4 x sin ( 4 x ) + 5
16 cos ( 4 x ) +C

Engineering Mathematics 11