Solved: Engineering Mathematics Assignment 1 with Explanations
VerifiedAdded on 2023/05/27
|9
|1274
|423
Homework Assignment
AI Summary
This document presents a detailed solution to Engineering Mathematics Assignment 1, covering topics such as phasor diagrams, AC circuits, centripetal force calculations, harmonic synthesis, and trigonometric identities. The solution demonstrates the application of phasor diagrams and trigonom...

Engineering Mathematics Assignment 1
ENGINEERING MATHEMATICS ASSIGNMENT
Name
Course
Professor
University
City/state
Date
ENGINEERING MATHEMATICS ASSIGNMENT
Name
Course
Professor
University
City/state
Date
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Engineering Mathematics Assignment 2
Engineering Mathematics Assignment
Task 1
Find the sum of v1 and v2 using a phasor diagram and appropriate trigonometry
Using a phasor diagram and appropriate trigonometry, find the sum of two alternative voltages
represented by: v1 = 60 sin (500t) and v2 = sin (500t + π
5 ¿
The relative positions of v1 and v2 when t = 0 are shown in form of phasor diagrams shown in
Figure 1 below where π
5 radians=36 °. The amplitude of the equations represents the length of
the phasor diagrams. The amplitude of v1 is 60V while th amplitude of v2 is 1V.
Figure 1: Sketch of phasor diagram
Drawing this phase diagram to scale using a protractor and ruler gives the diagram shown in
Figure 2 below
Engineering Mathematics Assignment
Task 1
Find the sum of v1 and v2 using a phasor diagram and appropriate trigonometry
Using a phasor diagram and appropriate trigonometry, find the sum of two alternative voltages
represented by: v1 = 60 sin (500t) and v2 = sin (500t + π
5 ¿
The relative positions of v1 and v2 when t = 0 are shown in form of phasor diagrams shown in
Figure 1 below where π
5 radians=36 °. The amplitude of the equations represents the length of
the phasor diagrams. The amplitude of v1 is 60V while th amplitude of v2 is 1V.
Figure 1: Sketch of phasor diagram
Drawing this phase diagram to scale using a protractor and ruler gives the diagram shown in
Figure 2 below

Engineering Mathematics Assignment 3
Figure 2: Phasor diagram drawn to scale
The resultant voltage, VR is measured and found to be 60.8V and the angle φ is measured to be
1°. This can also be expressed in radians as follows: 1 x π
180 =0.0175 rad leading v 1
Thus by drawing and measuring, the equation for v1 + v2 becomes:
vR = v1 + v2 = 60.8 sin (500t + 0.0175) V
Task 2
I. AC circuit is given by i = 100 sin (50πt – 0.43) amps. Find amplitude, angular
frequency, periodic time, frequency and phase angle
Amplitude = 100 amps
Angular frequency, ω = 50π rad/s
Frequency, f is obtained from the angular frequency as follows
ω = 50π rad/s = 2πf; hence f = ω
2 π = 50 π
2 π =25 Hz
Figure 2: Phasor diagram drawn to scale
The resultant voltage, VR is measured and found to be 60.8V and the angle φ is measured to be
1°. This can also be expressed in radians as follows: 1 x π
180 =0.0175 rad leading v 1
Thus by drawing and measuring, the equation for v1 + v2 becomes:
vR = v1 + v2 = 60.8 sin (500t + 0.0175) V
Task 2
I. AC circuit is given by i = 100 sin (50πt – 0.43) amps. Find amplitude, angular
frequency, periodic time, frequency and phase angle
Amplitude = 100 amps
Angular frequency, ω = 50π rad/s
Frequency, f is obtained from the angular frequency as follows
ω = 50π rad/s = 2πf; hence f = ω
2 π = 50 π
2 π =25 Hz
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Engineering Mathematics Assignment 4
Periodic time, T = 1
f = 1
25 =0.04 s
Phase angle = 0.43 radians lagging or 180°
π x 0.43=24.64 °lagging
Therefore the phase angle is lagging i = 100 sin (50πt)
II. Determine the change in acceleration
Centripetal acceleration is calculated using the following equation, ac = v ²
r ; where v = speed of
the object in m/s and r = radius of arc (Bird & Ross, 2014); (Bird, 2015).
Converting speed into m/s gives: v = 34 km/h = 34
3.6 = 9.44 m/s
r1 = 100 m and r2 = 150 m
Acceleration in first arc (i.e. when r = 100m) = (9.44 m/ s) ²
100 m =0.89 m/s ²
Acceleration in second arc (i.e. when r = 150m) = (9.44 m/ s) ²
150 m =0.59 m/s ²
Change in acceleration = 0.89 m/s2 – 0.59 m/s2 = 0.3 m/s2
III. Calculate the centripetal force
The centripetal force acting on the vehicle is calculated using the following equation F= mv ²
r ;
where F = force in Newtons (N), m = mass in kilograms (kg), v = speed in metres per second
(m/s) and r = radius in meters (m).
Periodic time, T = 1
f = 1
25 =0.04 s
Phase angle = 0.43 radians lagging or 180°
π x 0.43=24.64 °lagging
Therefore the phase angle is lagging i = 100 sin (50πt)
II. Determine the change in acceleration
Centripetal acceleration is calculated using the following equation, ac = v ²
r ; where v = speed of
the object in m/s and r = radius of arc (Bird & Ross, 2014); (Bird, 2015).
Converting speed into m/s gives: v = 34 km/h = 34
3.6 = 9.44 m/s
r1 = 100 m and r2 = 150 m
Acceleration in first arc (i.e. when r = 100m) = (9.44 m/ s) ²
100 m =0.89 m/s ²
Acceleration in second arc (i.e. when r = 150m) = (9.44 m/ s) ²
150 m =0.59 m/s ²
Change in acceleration = 0.89 m/s2 – 0.59 m/s2 = 0.3 m/s2
III. Calculate the centripetal force
The centripetal force acting on the vehicle is calculated using the following equation F= mv ²
r ;
where F = force in Newtons (N), m = mass in kilograms (kg), v = speed in metres per second
(m/s) and r = radius in meters (m).
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Engineering Mathematics Assignment 5
First is to convert the mass of the vehicle from tonnes to kg and the speed of the vehicle from
km/h to m/s before applying the equation
m = 0.85 tonnes = 850 kg
v = 60 km/h = 60
3.6 = 16.67 m/s
r = 75 m
F=(850 kg) x (16.67 m/s)²
75 m =3,148.15 N
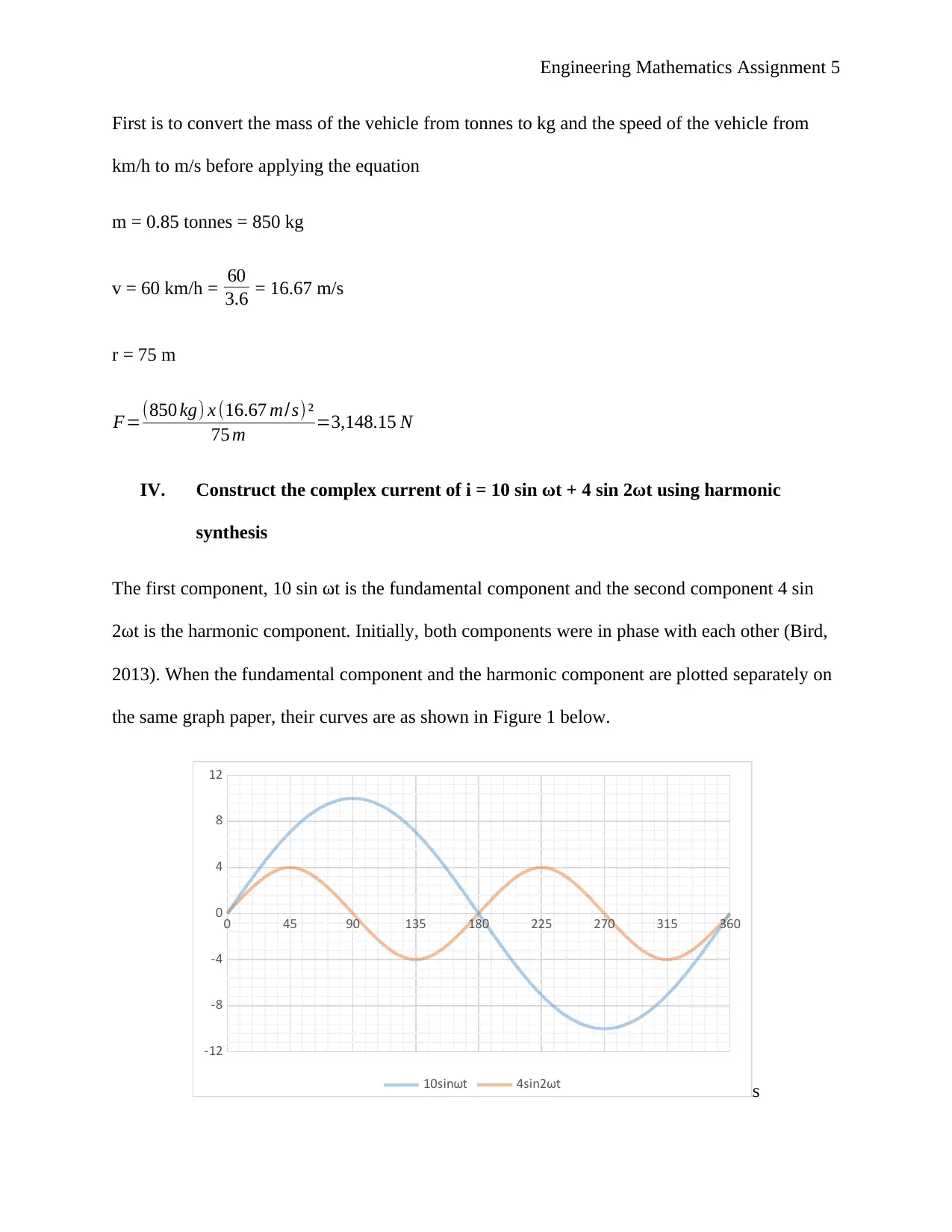
IV. Construct the complex current of i = 10 sin ωt + 4 sin 2ωt using harmonic
synthesis
The first component, 10 sin ωt is the fundamental component and the second component 4 sin
2ωt is the harmonic component. Initially, both components were in phase with each other (Bird,
2013). When the fundamental component and the harmonic component are plotted separately on
the same graph paper, their curves are as shown in Figure 1 below.
0 45 90 135 180 225 270 315 360
-12
-8
-4
0
4
8
12
10sinωt 4sin2ωt s
First is to convert the mass of the vehicle from tonnes to kg and the speed of the vehicle from
km/h to m/s before applying the equation
m = 0.85 tonnes = 850 kg
v = 60 km/h = 60
3.6 = 16.67 m/s
r = 75 m
F=(850 kg) x (16.67 m/s)²
75 m =3,148.15 N
IV. Construct the complex current of i = 10 sin ωt + 4 sin 2ωt using harmonic
synthesis
The first component, 10 sin ωt is the fundamental component and the second component 4 sin
2ωt is the harmonic component. Initially, both components were in phase with each other (Bird,
2013). When the fundamental component and the harmonic component are plotted separately on
the same graph paper, their curves are as shown in Figure 1 below.
0 45 90 135 180 225 270 315 360
-12
-8
-4
0
4
8
12
10sinωt 4sin2ωt s
Engineering Mathematics Assignment 6
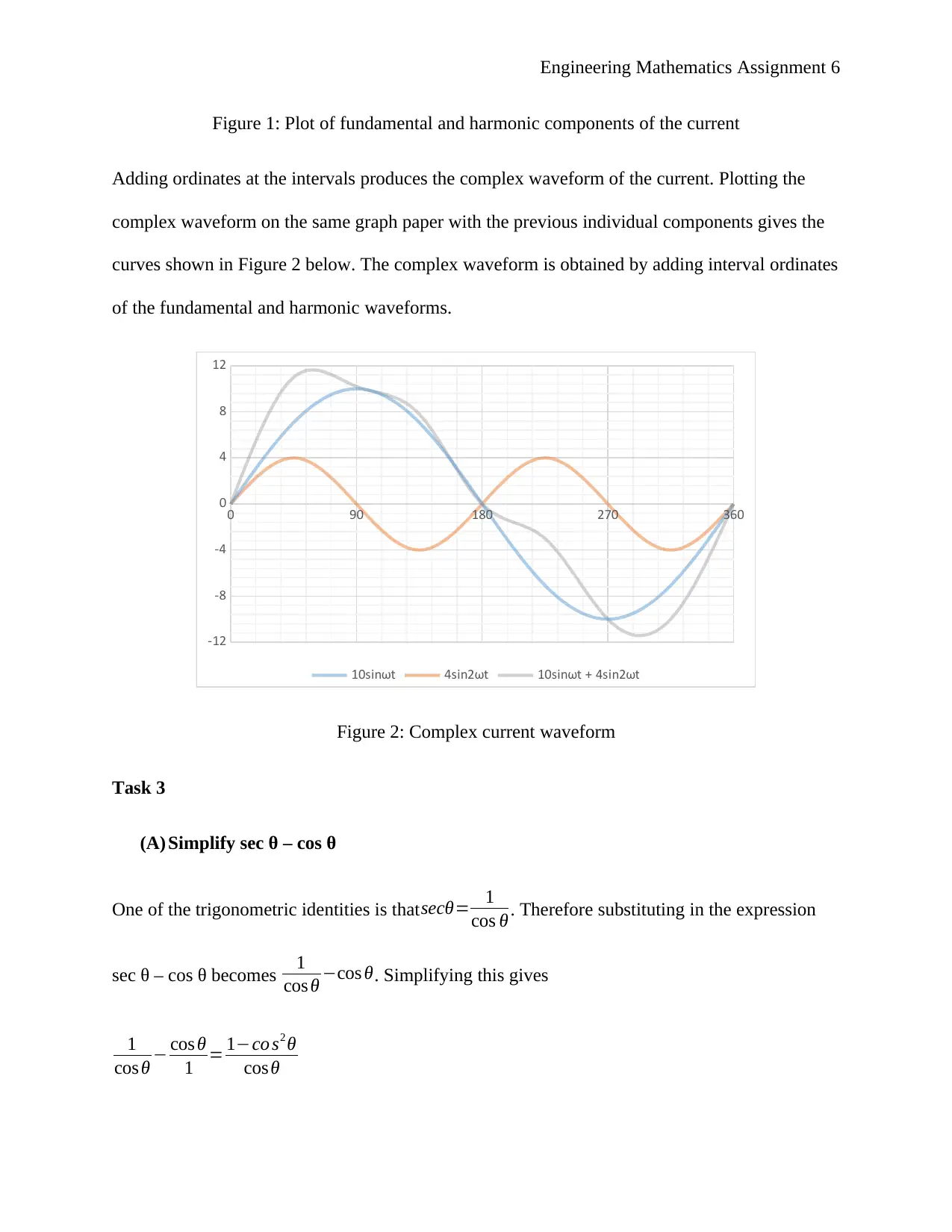
Figure 1: Plot of fundamental and harmonic components of the current
Adding ordinates at the intervals produces the complex waveform of the current. Plotting the
complex waveform on the same graph paper with the previous individual components gives the
curves shown in Figure 2 below. The complex waveform is obtained by adding interval ordinates
of the fundamental and harmonic waveforms.
0 90 180 270 360
-12
-8
-4
0
4
8
12
10sinωt 4sin2ωt 10sinωt + 4sin2ωt
Figure 2: Complex current waveform
Task 3
(A) Simplify sec θ – cos θ
One of the trigonometric identities is that secθ= 1
cos θ . Therefore substituting in the expression
sec θ – cos θ becomes 1
cos θ −cos θ. Simplifying this gives
1
cos θ − cos θ
1 = 1−co s2 θ
cos θ
Figure 1: Plot of fundamental and harmonic components of the current
Adding ordinates at the intervals produces the complex waveform of the current. Plotting the
complex waveform on the same graph paper with the previous individual components gives the
curves shown in Figure 2 below. The complex waveform is obtained by adding interval ordinates
of the fundamental and harmonic waveforms.
0 90 180 270 360
-12
-8
-4
0
4
8
12
10sinωt 4sin2ωt 10sinωt + 4sin2ωt
Figure 2: Complex current waveform
Task 3
(A) Simplify sec θ – cos θ
One of the trigonometric identities is that secθ= 1
cos θ . Therefore substituting in the expression
sec θ – cos θ becomes 1
cos θ −cos θ. Simplifying this gives
1
cos θ − cos θ
1 = 1−co s2 θ
cos θ
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Engineering Mathematics Assignment 7
But sin2θ + cos2θ = 1 → 1 – cos2θ = sin2θ
Hence the above expression becomes sin ² θ
cos θ
Also sin θ
cos θ =tanθ
Thus the above expression becomes sin θ sinθ
cos θ =( sin θ
cos θ ) (sin θ)= tanθsinθ
(B) Find the values of x if 4sin2θ + 2.5 = 5cosθ
Find all possible values of x, using the appropriate identity if: 4sin2θ + 2.5 = 5cosθ, within the
range 0°≤x≤360°
The identity of sin θ and cos θ is: sin2θ + cos2θ = 1
→ sin2θ = 1 – cos2θ; substituting this in the original equation gives:
4(1 – cos2θ) + 2.5 = 5cosθ
4 – 4cos²θ + 2.5 = 5cosθ
-4cos²θ – 5cosθ + 6.5 = 0
4cos²θ + 5cosθ – 6.5 = 0
The above equation can be solved for cos θ using the quadratic equation −b ± √ b2−4 ac
2a as
follows:
cos θ = −5 ± √ 52−(4 x 4 x−6.5)
2 x 4 =−5 ± √ 25−(−104)
8 =−5± √ 129
8 =−5± 11.358
8
But sin2θ + cos2θ = 1 → 1 – cos2θ = sin2θ
Hence the above expression becomes sin ² θ
cos θ
Also sin θ
cos θ =tanθ
Thus the above expression becomes sin θ sinθ
cos θ =( sin θ
cos θ ) (sin θ)= tanθsinθ
(B) Find the values of x if 4sin2θ + 2.5 = 5cosθ
Find all possible values of x, using the appropriate identity if: 4sin2θ + 2.5 = 5cosθ, within the
range 0°≤x≤360°
The identity of sin θ and cos θ is: sin2θ + cos2θ = 1
→ sin2θ = 1 – cos2θ; substituting this in the original equation gives:
4(1 – cos2θ) + 2.5 = 5cosθ
4 – 4cos²θ + 2.5 = 5cosθ
-4cos²θ – 5cosθ + 6.5 = 0
4cos²θ + 5cosθ – 6.5 = 0
The above equation can be solved for cos θ using the quadratic equation −b ± √ b2−4 ac
2a as
follows:
cos θ = −5 ± √ 52−(4 x 4 x−6.5)
2 x 4 =−5 ± √ 25−(−104)
8 =−5± √ 129
8 =−5± 11.358
8
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Engineering Mathematics Assignment 8
cos θ = 0.79475 or cos θ = -2.04475
But cos θ cannot be -2.04475
Therefore cos θ = 0.79475 → θ = cos-1 0.79475 = 37.37°
For the interval 0°≤x≤360°, θ = 37.37° or 322.63°
(C) Find sinh x given that cosh x=¿ 5
4 ¿
Given that cosh x=¿ 5
4 ¿; using the appropriate identity, find the value of sinh x
The identity of sinhx and cosh x is: cosh2x – sinh2x = 1
Substituting cosh x=¿ 5
4 ¿ in the above expression gives
( 5
4 )
2
−sin h2 x=1
25
16 −sin h2 x=1
sinh ² x=¿ 25
16 −1 ¿
sinh ² x=¿ 0.5625 ¿
sinh x = √0.5625 = ± 0.75
Hence sinh x=¿ ± 3
4 ¿
cos θ = 0.79475 or cos θ = -2.04475
But cos θ cannot be -2.04475
Therefore cos θ = 0.79475 → θ = cos-1 0.79475 = 37.37°
For the interval 0°≤x≤360°, θ = 37.37° or 322.63°
(C) Find sinh x given that cosh x=¿ 5
4 ¿
Given that cosh x=¿ 5
4 ¿; using the appropriate identity, find the value of sinh x
The identity of sinhx and cosh x is: cosh2x – sinh2x = 1
Substituting cosh x=¿ 5
4 ¿ in the above expression gives
( 5
4 )
2
−sin h2 x=1
25
16 −sin h2 x=1
sinh ² x=¿ 25
16 −1 ¿
sinh ² x=¿ 0.5625 ¿
sinh x = √0.5625 = ± 0.75
Hence sinh x=¿ ± 3
4 ¿

Engineering Mathematics Assignment 9
References
Bird, J., 2013. Understanding Engineering Mathematics. Abingdon: Routledge.
Bird, J., 2015. Science for Engineering. 5th ed. Abingdon-on-Thames: Routledge.
Bird, J. & Ross, C., 2014. Mechanical Engineering Principles. 3rd ed. Abingdon-on-Thames, UK:
Routledge.
References
Bird, J., 2013. Understanding Engineering Mathematics. Abingdon: Routledge.
Bird, J., 2015. Science for Engineering. 5th ed. Abingdon-on-Thames: Routledge.
Bird, J. & Ross, C., 2014. Mechanical Engineering Principles. 3rd ed. Abingdon-on-Thames, UK:
Routledge.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





