logo

Engineering Mathematics Assignment

   

Added on  2020-04-21

13 Pages1055 Words47 Views
Engineering MathematicsStudent Name:University 21st January 2018
Engineering Mathematics Assignment_1
Task 1:1)Simplify 6x2+7x−5x−1 by dividing.Solution6x2+7x−5x−1=6x2+10x−3x−5x−1=2x(3x+5)−1(3x+5)x−1=(3x+5)(2x−1)x−1=2(3x+5)2)Resolve the following into partial fractions.a)x−11x2−x−2Solutionx2−x−2=x2−2x+x−2=x(x−2)+1(x−2)=(x+1)(x−2)x−11x2−x−2=x−11(x+1)(x−2)=Ax+1+Bx−2x−11(x+1)(x−2)=A(x−2)+B(x+1)(x+1)(x−2)x−11=A(x−2)+B(x+1)x−11=Ax−2A+Bx+Bx=Ax+BxA+B=1−2A+B=−113A=12A=44+B=1B=−3Thus the answer is;Ax+1+Bx−2=4x+1−3x−24x+1−3x−2b)
Engineering Mathematics Assignment_2
3−x(x¿¿2+3)(x+3)¿Solution3−x(x¿¿2+3)(x+3)=A(x¿¿2+3)+B(x+3)+Cx=A+B+Cx3+3x2+3x+9=A+B+Cx2(x+3)+3(x+3)=A+B+Cx2(x+3)+3(x+3)¿¿3−x(x¿¿2+3)(x+3)=A(x+3)+B(x¿¿2+3)+Cx(x¿¿2+3)(x+3)¿¿¿3−x=A(x+3)+B(x¿¿2+3)+Cx¿3−x=Ax+3A+Bx2+3B+CxAx+2Bx=−xA−B=−13A+3B=34A=2A=1212−B=−1B=32C=1Thus the answer is;A(x¿¿2+3)+B(x+3)=1/2(x¿¿2+3)+3/2(x+3)¿¿Task 2:3)We have;Temp, t(mins)246810Temp185161140122106
Engineering Mathematics Assignment_3
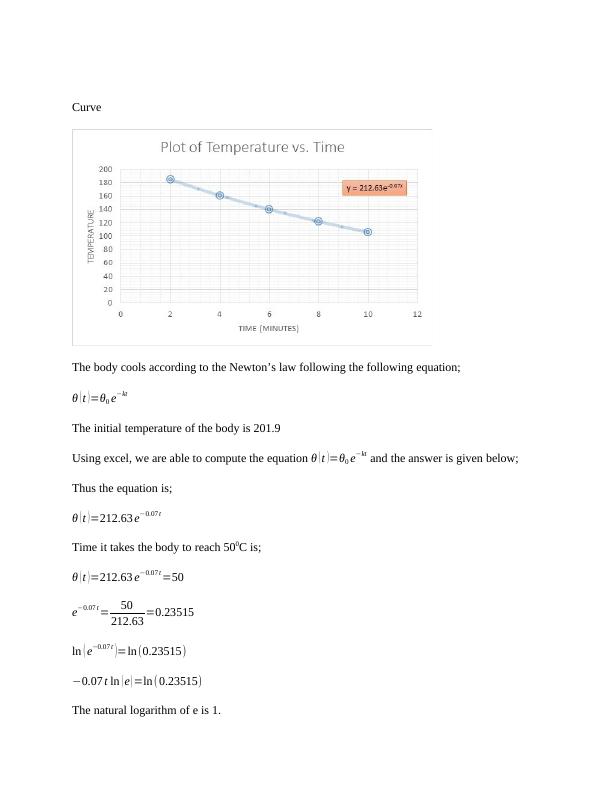
CurveThe body cools according to the Newton’s law following the following equation;θ(t)=θ0e−ktThe initial temperature of the body is 201.9Usingexcel,weareabletocomputetheequation θ(t)=θ0e−kt and the answer is given below;Thus the equation is;θ(t)=212.63e−0.07tTime it takes the body to reach 500C is;θ(t)=212.63e−0.07t=50e−0.07t=50212.63=0.23515ln(e−0.07t)=ln(0.23515)−0.07tln(e)=ln(0.23515)Thenatural logarithmofeis1.
Engineering Mathematics Assignment_4

End of preview

Want to access all the pages? Upload your documents or become a member.

Related Documents
Mathematics And Computing Assignment
|18
|2652
|331