Electrical Engineering: Circuit Analysis and Vector Algebra Homework

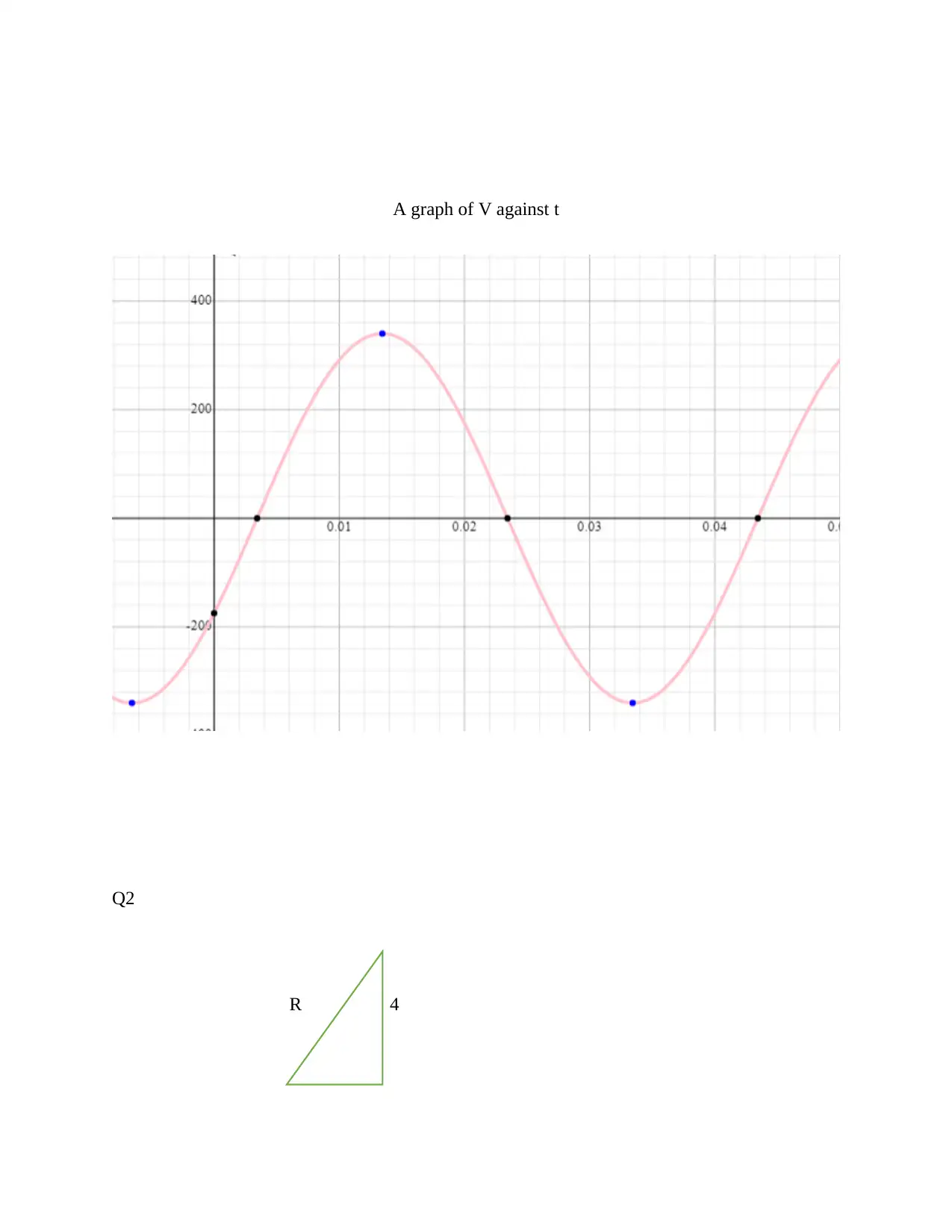
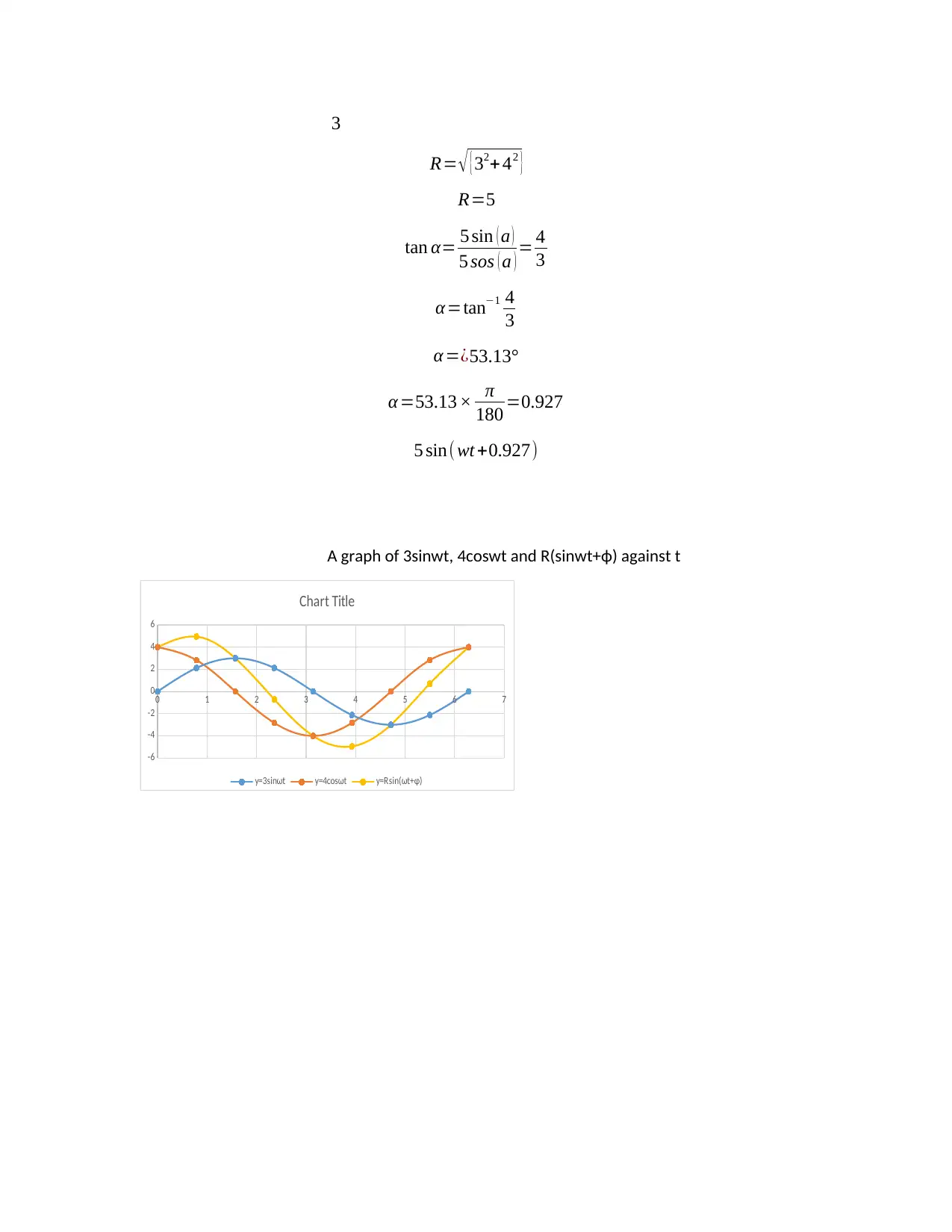
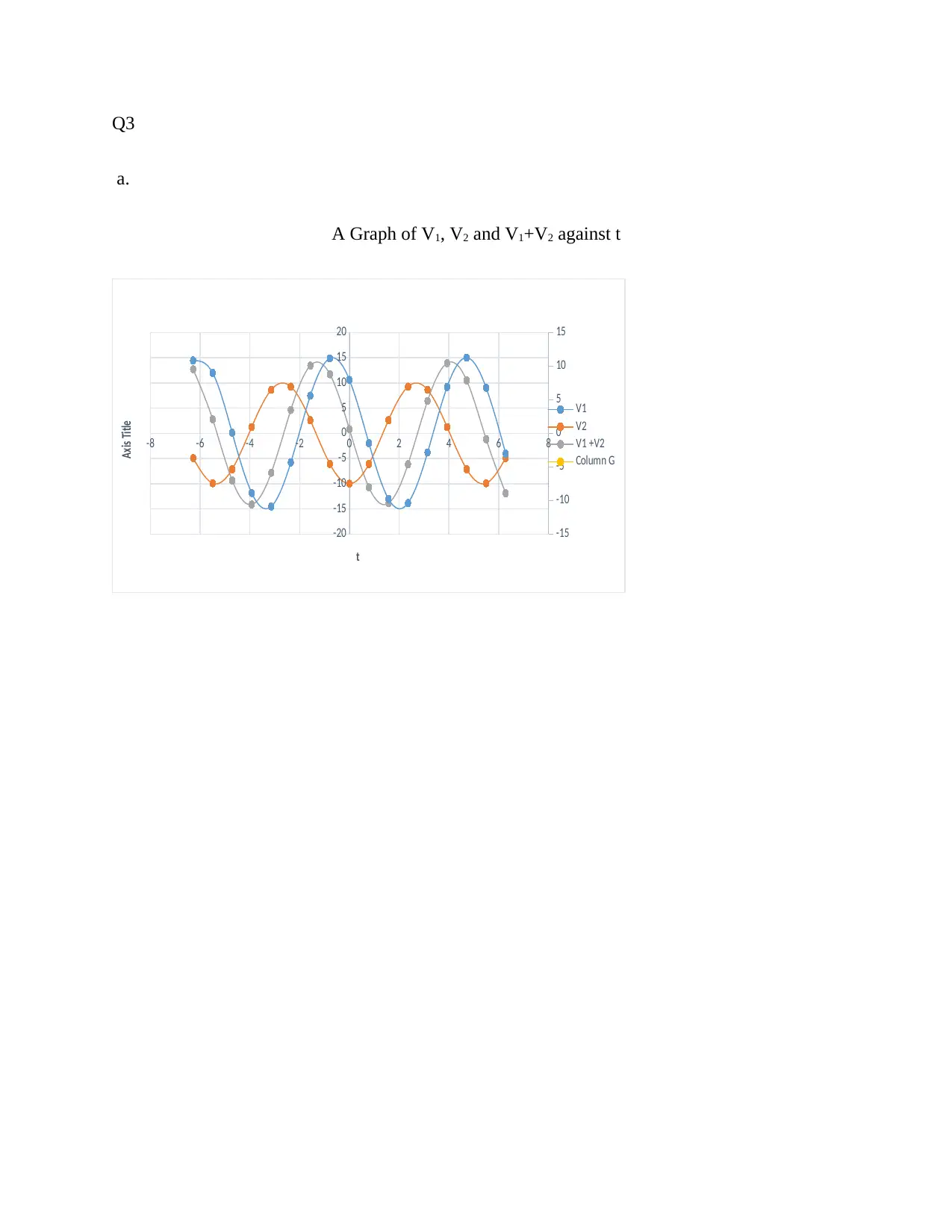
This document presents a comprehensive solution to an electrical engineering assignment. The solution encompasses several key areas of electrical engineering, including the analysis of sinusoidal waveforms, determination of amplitude, phase angle, and periodic time. It further explores circu...Read More

Q1.
a.
Amplitude=34 0 V
Periodic time , T =2 π
w
w=50 π rads/ s
T =0.04 s
Phase angle=−0.541 rads
Phase angle=−.541× 180 °
π
Phase angle=−30.997 °
b.
V =340sin ( 50 πt−30.997 )
t=0 s
V =340sin ( 0−30.997 )
V =340sin (−30.997 )
V =340×−.4068
V =−138.312V
c.
angle θ °=50 π × 0.01× 180
π
θ=90 °
V =340sin (90−30.997)
V =340sin ( 59.003 ° )
V =215.696V
d.
angle β ° =50 πt × 180
π =9000t
200 V =340 V ×sin ( 9000 t−30.997 )

9000 t−30.997=sin−1 ( 200
340 )¿
9000 t=30.997+36.03
t= 67.027
9000
t=0.00745 s
e.
At max voltage ,
sin ( 9000 t −30.997 ) =1
9000 t−30.997=sin−1 1❑
9000 t=90+30.997
t= 120.997
9000
t=0.0134 s
f.
at t=0 ,
V =340sin (−0.541 )=−175.098 V
at V =0 ,
sin ( 50 πt−0.541 )=0
50 πt−0.541=0
t=0.00344 s
at V =V max
d V
d t =0=340 cos ( 50 πt−0.541 ) × 50 π
cos ( 50 πt−0.541 ) =0=cos π
2
50 πt−0.541= π
2
t=0.01344 s
at next x intercept , 1
2 cycle
t=0.01344+ ( 0.01344−0.00344 )
¿ 0.02344 s
at 3
4 cycle
t=0.03344 s
at full cycle
t=0.04344 s

A graph of V against t
Q2
R 4

3
R= √ {32+ 42 }
R=5
tan α= 5 sin ( a )
5 sos ( a ) = 4
3
α =tan−1 4
3
α =¿53.13°
α =53.13 × π
180 =0.927
5 sin(wt +0.927)
A graph of 3sinwt, 4coswt and R(sinwt+ϕ) against t
0 1 2 3 4 5 6 7
-6
-4
-2
0
2
4
6
Chart Title
y=3sinωt y=4cosωt y=Rsin(ωt+φ)

Q3
a.
A Graph of V1, V2 and V1+V2 against t
-8 -6 -4 -2 0 2 4 6 8
-20
-15
-10
-5
0
5
10
15
20
-15
-10
-5
0
5
10
15
V1
V2
V1 +V2
Column G
t
Axis Title

b.
i.
15 sin (20 πt+ π
4 )+10 sin (20 πt− π
2 )
15 ( sin 20 πt ) cos ( π
4 )+cos ( 20 πt ) sin ( π
4 )¿+¿ 10 ¿
15 ( 0.7071 sin (20 πt)+0.7071 cos ( 20 πt ) ) −10 cos (20 πt)
10.6065 sin (20 πt)+10.6065 cos (20 πt )
10.6065 sin ( 20 πt ) −0.6065 cos ( 20 πt )
R= √ 10.60652 +0.60652 =10.623
10.6065
R 0.6025
tan ( φ )= 0.6065
10.6065
φ

φ=−0.005326 rads
V 1 +V 2=10.623 sin ( 20 πt−0.005326)
ii.
From the graph, the value the amplitude of V1 + V2 was found to be 10.625. From
calculation, the amplitude was found to be 10.623. There is a slight error of 0.002.
This show that both the empirical and the analytical solution bring the same result.
The graph of V1 +V2 lags by 2.43 radians from the empirical solution. However,
from the analytical solution, the curve lags by 0.005326radians.
Q4.
r1 × F1=
| i j k
3 1 5
2 −1 1|
¿ i ( 1+5 )− j ( 3−10 )+k (−3−2)
¿ 6 i+7 j−5 k
r2 × F2=
|i j k
5 −2 −1
8 −6 6 |
¿ i ( −12−6 ) − j ( 30+8 ) +k (−30+16)

¿−18 i−38 j−14 k
r3 × F3=
| i j k
1 −6 7
4 0 3|
¿ i (−18−0 )− j ( 3−28 )+k (0+ 24)
¿−18 i+25 j+24 k
r 4 × F4 =
|i j k
1 0 6
1 −5 0|
¿ i ( 0+30 ) − j ( 0−6 ) + k (−5−0)
¿ 30 i+ 6 j−5 k
(r ¿¿ 1 × F1)+¿ ¿ ¿
¿+ ( −18 i−38 j−14 k ) + ( −18i +25 j+24 k ) +(30i+6 j−5 k )
¿ 6 i−18 i−18 i+ 30i+7 j−38 j+25 j+6 j−5 k −14 k +24 k−5 k =0
References

Singh, K., 2011. Engineering mathematics through applications. Macmillan International Higher
Education.
Stroud, K.A. and Booth, D.J., 2013. Engineering mathematics. Macmillan International Higher
Education