Engineering Mathematics

This document discusses the partial differential equation of the wave equation, its separation into functions of t and x, and the boundary conditions. It also covers the analytical and numerical solutions of the wave equation, including the discretized equation and the stability criteria. MATLAB code and plots are provided for better understanding.

Running head: ENGINEERING MATHEMATICS
ENGINEERING MATHEMATICS
Name of the Student
Name of the University
Author Note

1ENGINEERING MATHEMATICS
Section 1:
1. The partial differential equation of the wave equation is given by,
( ∂2
∂ t2 )u ( x , t ) – c2∗( ∂2
∂ x2 )u ( x , t ) =0 (1)
Now, let u ( x , t ) can be separated in functions of t and x
u(x,t) = g(x)*f(t) which is a solution of the wave equation.
Hence, equation (1) becomes
g ( x )∗f ’ ’ ( t )=c2∗f ( t )∗g ’ ’ ( x )
 g ( x )
g ’ ’ ( x ) =c2∗f ( t )
f ’’ ( t ) (1)
The boundary conditions are the left and the right end are held at height zero.
u(0,t) = 0 for t>0
u(L,t) = 0 for t>0
where, L = length of the string = 0.5 m
Now, the initial displacement is 0 and initial velocity is induced by a sonic wave inducer and
thus it is also 0 as the initial displacement is 0.
Hence, u(0,0) = 0 and du ( 0,0 )
dt = 0
2.
Now, left and right side of the equation (1) is constant let σ.
Hence, g’’(x) – σg(x) = 0. Now, assuming auxiliary solution as exp(rx)

2ENGINEERING MATHEMATICS
( d2
d x2 )exp ( rx ) – σ exp ( rx )=0 (A)
 ( r2 −σ )∗exp ( rx )=0 => r = ±√σ
Also, ( d2
d t2 ) exp ( st ) – c2 exp ( st ) =0 (B)
Assuming exp(st) as the auxiliary solution we get
( s2 – c2 σ ) exp ( st )=0 => s^2 – c^2σ = 0 => s = ±c√σ
Hence, the two independent solution of (A) are exp(c √ σ t ¿ and exp(-c√σ t)
Hence, the general solutions are
X(x) = d1*exp(c √ σ t ¿ + d2*exp(-c√σ t) and T(t) = d3*exp(c√ σ t ¿ + d4*exp(-c√σ t)
Here, d1, d2, d3 and d4 are arbitrary constants.
Now, when σ ≠ 0 then g(x) =0 satisfied when d1 + d2 = 0 => d2 = -d1.
Also, the condition g(L) = 0 is satisfied when
d1*exp( √σ t ¿ + d2*exp(- √ σ t) = 0 => d1(exp(√ σ t ¿−exp(− √ σ t)¿ = 0
Hence, exp(√ σ t ¿−exp(− √ σ t) = 0 => exp(2 √σ L) = 1
Now, there are infinitely many complex numbers that satisfy the above equation and exp(2
√ σ L) = 1 when for any integer k
2√ σ L = 2kπi => √σ = kπi/L => σ = −k2∗π2
L2
Hence, g(x)*f(t) = d1(exp(ikπx/L) – exp(-ikπx/L))(d3exp(ickπt/L) + d4exp(-ickπt/L))
= 2i*d1*sin(kπx/L)[(d3 + d4)cos(ckπt/L) + i(d3 – d4)sin(ckπt/L)]

3ENGINEERING MATHEMATICS
= sin(kπx/L)[αk*cos(ckπt/L) + βksin(ckπt/L)]
Here, αk = 2id1(d3 + d4) and βk = -2d1(d3-d4).
Now, imposing initial condition we get,
u(x,t) = ∑
k =1
∞
sin ( kπx
L ) [αk∗cos ( ckπt
L ) + βk∗sin ( ckπt
L ) ]
The Fourier coefficients needs to satisfy the equations
f(x) = u(x,0) = ∑
k =1
∞
αk∗sin ( kπx
L )
g(x) = du(x,0)/dt = ∑
k =1
∞
βk∗( ckπ
L ) sin ( kπx
L )
Here, the Fourier coefficients are
αk = (2/L) ∫
0
L
f ( x ) sin ( kπx
L ) dx and βk = ( 2
ckπ )∫
0
L
g ( x ) sin ( kπx
L ) dx
3.
The velocity profile is given below,
( ∂
∂ t )u ( x ,0 )= A ( 2 πf 3 ) sin ( 3 πx
L )
A = 1e-3 m, f3 = 540 Hz.
Now, differentiating with respect to t the solution in general form is given by,
u(x , t)=∑
k=1
∞
sin ( kπx
L )[α k cos ( ckπ
L t )+ βk sin ( ckπ
L t )]
Now, the 3rd mode sine wave is given by,

4ENGINEERING MATHEMATICS
u(x , t)=∑
k=1
∞
sin ( 3 πx
L ) [αk cos ( 3 cπ
L t )+ βk sin ( 3 cπ
L t ) ]
Now, the frequency is given as 3rd mode sine wave f3 = 540 Hz.
Now, f3 = c/2L => c = 2Lf3 = 2*0.5*540 = 540 rad/sec.
4.
The discretized equation of the 1D wave equation (1) will be
xi
n +1−2 xi
n+xi
n−1
Δ t2 = c2 xi
n+1−2 xi
n + xi
n−1
Δ x2
Or, xi
n+1=2 xi
n−xi
n−1 +¿ [ c∗Δt
Δx ]
2
(xi+1
n −2 xi
n + xi −1
n ¿
Here, the c∗Δt
Δx = CFL number (Courant-Friedrichs-Lewy number). The number is chosen in
such a way that the numerical speed is less than the propagation speed.
Or, Δt
Δx < c.
The maximum stable time-step for a grid spacing is Δx
L =2−2
The stability criteria of the system is
[ c∗Δt
Δx ]2
<=1 Or, Δx
Δt ≥ c
Section 2:
Now, the numerical solution is obtained by finite differential method of solving partial
differential equation. The waves are assumed to have reflection boundary i.e. the waves
reflects back from the left and right boundaries of the rig. The analytical solution is obtained

5ENGINEERING MATHEMATICS
in 3D plot where time, displacement and amplitude of the wave is displayed. For different
grid points the solution is obtained.
MATLAB code:
clc
clear
Lx = 0.5; % length of the test rig is 0.5 meters
dx = 0.01; % unit increment of displacemnt x
nx = 128; %grid size
x = linspace(0,Lx,nx);
T= 2; % time for simulation is 5 secs
xn = zeros(nx,1); %
xnm1 = xn;
xnp1 = xn;
CFL = 1; % CFL number is 1

6ENGINEERING MATHEMATICS
c = 1;
dt = CFL*dx/c; % c = CFL*(dx/dt)
% creating a disturbance or wave in the middle of the rig that will
% propagate
xn(73:75) = [0.1 0.2 0.1];
xnp1(:) = xn(:);
t=0; % staring time t=0
while t<T
xn([1 end])=0;
t = t+dt;
xnm1 = xn;
xn = xnp1;
for i=2:nx-1
xnp1(i) = 2*xn(i) - xnm1(i) + CFL^2*(xn(i+1) - 2*xn(i) + xn(i-1)); % implementing
discretized equation

7ENGINEERING MATHEMATICS
end
clf;
plot(x,xn)
xlabel('length of rig')
ylabel('Displacement')
grid on
title(sprintf('time=%.2f sec',t));
axis([0 Lx -0.5 0.5]);
shg; pause(0.00001)
end
time = linspace(0,T,length(x));
xtanlytic = cos(pi*time)'*sin(pi*x);
figure
mesh(x,time,xtanlytic)
xlabel('Distance(x) \rightarrow')
ylabel('\leftarrow Time(t)')
zlabel('Amplitude \rightarrow')
title('Analytical solution in 3D plane')

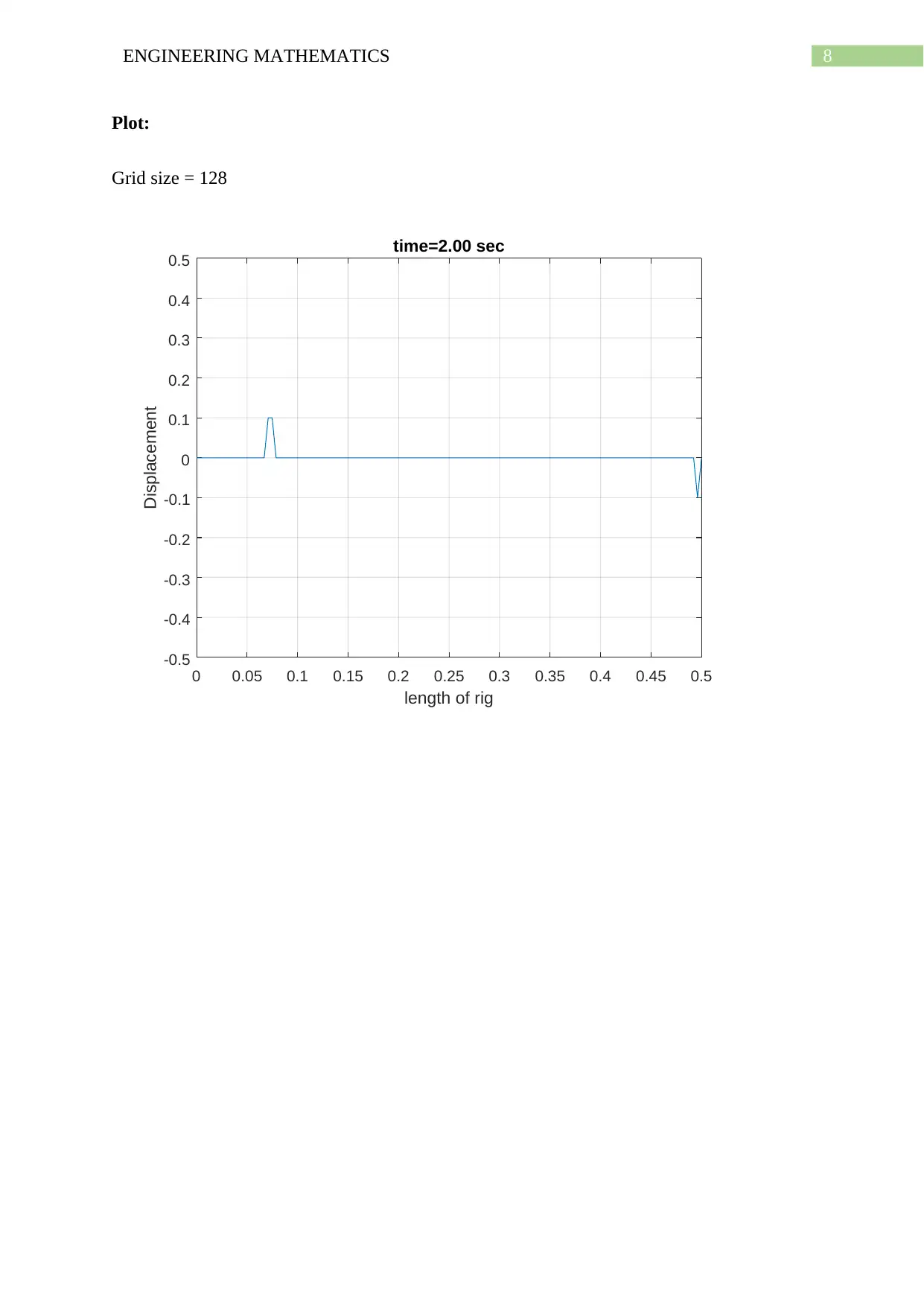
8ENGINEERING MATHEMATICS
Plot:
Grid size = 128
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
length of rig
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Displacement
time=2.00 sec

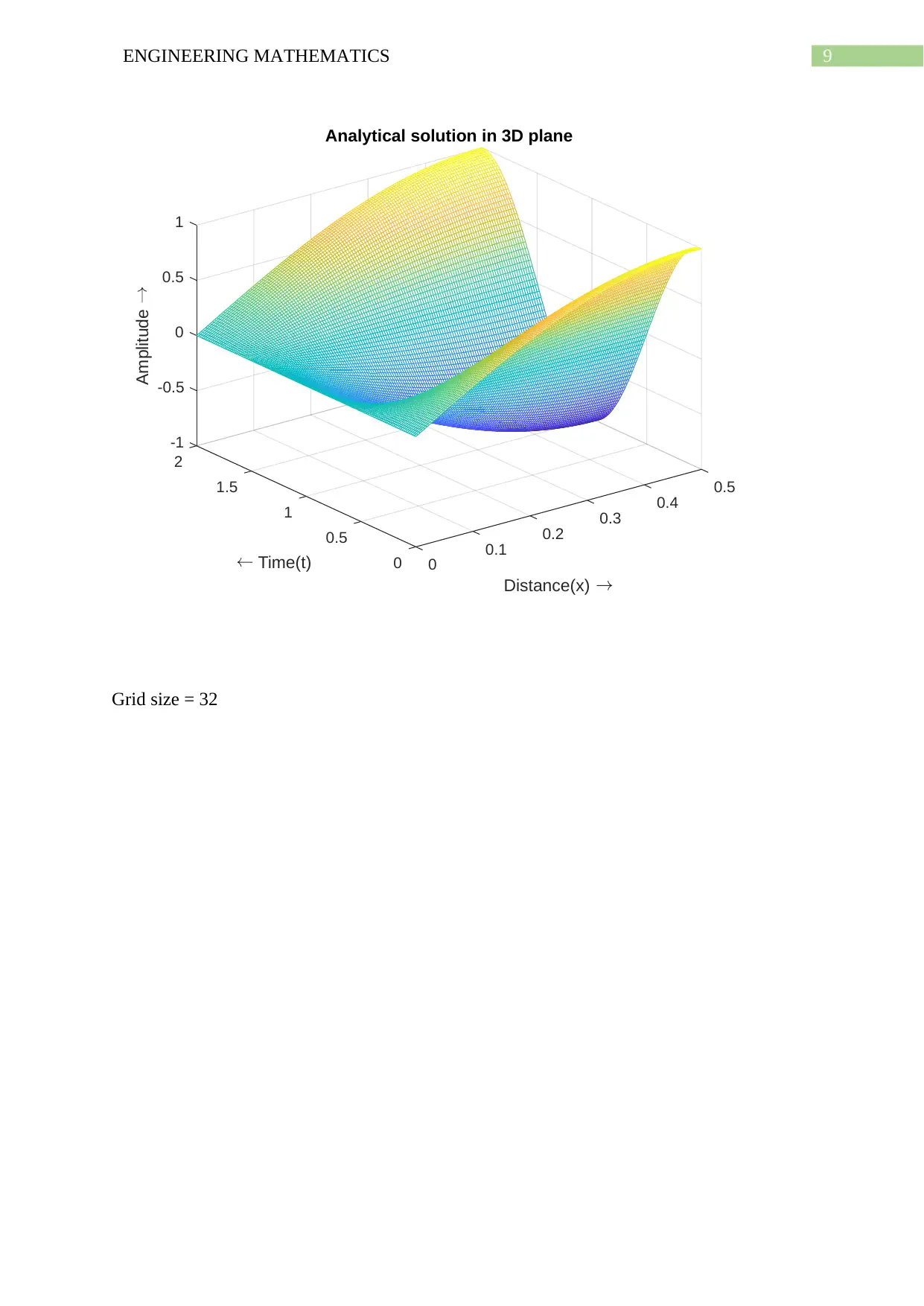
9ENGINEERING MATHEMATICS
-1
2
-0.5
1.5 0.5
0
Amplitude
0.4
Analytical solution in 3D plane
0.5
Time(t)
1 0.3
Distance(x)
1
0.20.5 0.1
0 0
Grid size = 32

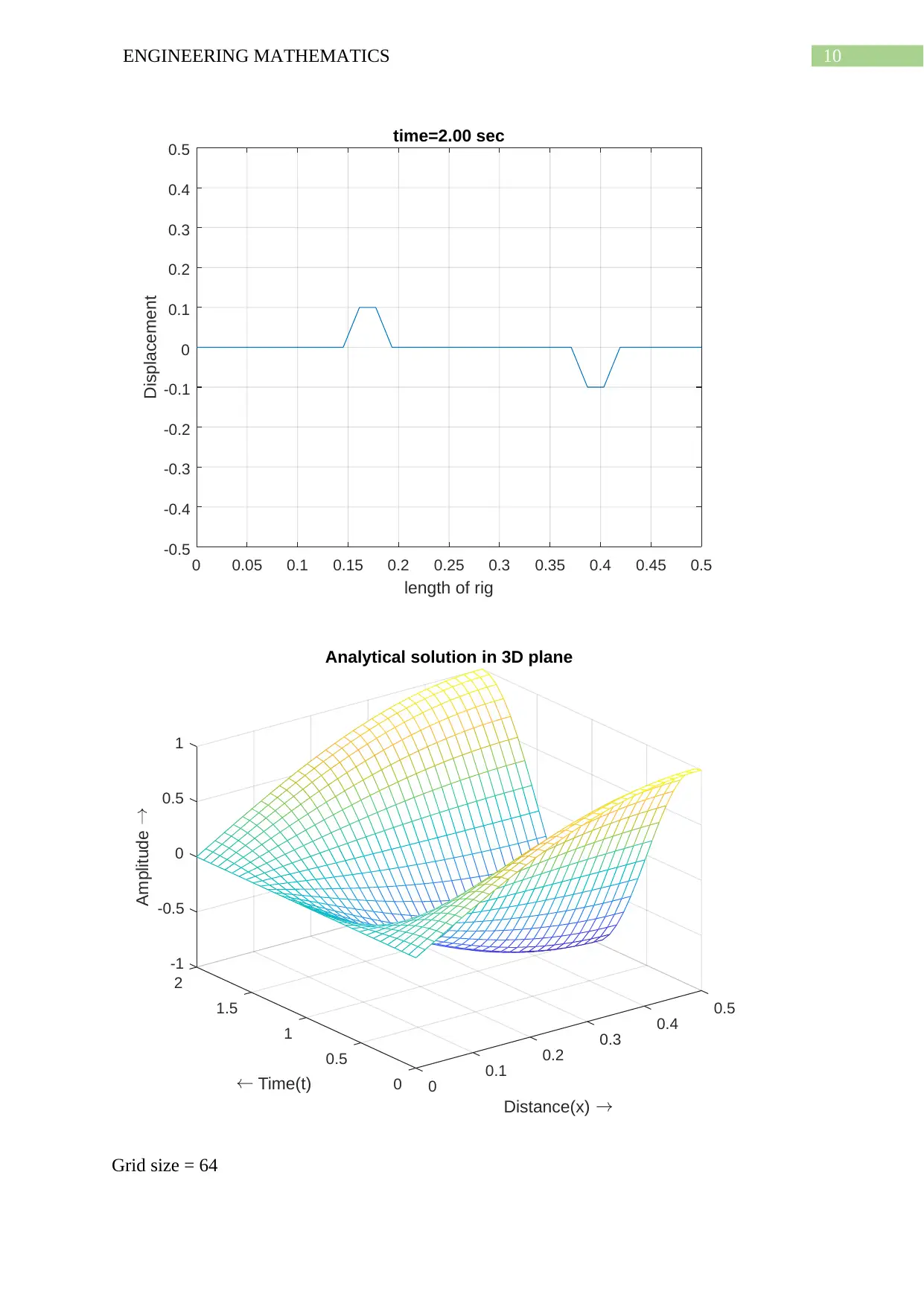
10ENGINEERING MATHEMATICS
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
length of rig
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Displacement
time=2.00 sec
-1
2
-0.5
1.5 0.5
0
Amplitude
0.4
Analytical solution in 3D plane
0.5
Time(t)
1 0.3
Distance(x)
1
0.20.5 0.1
0 0
Grid size = 64

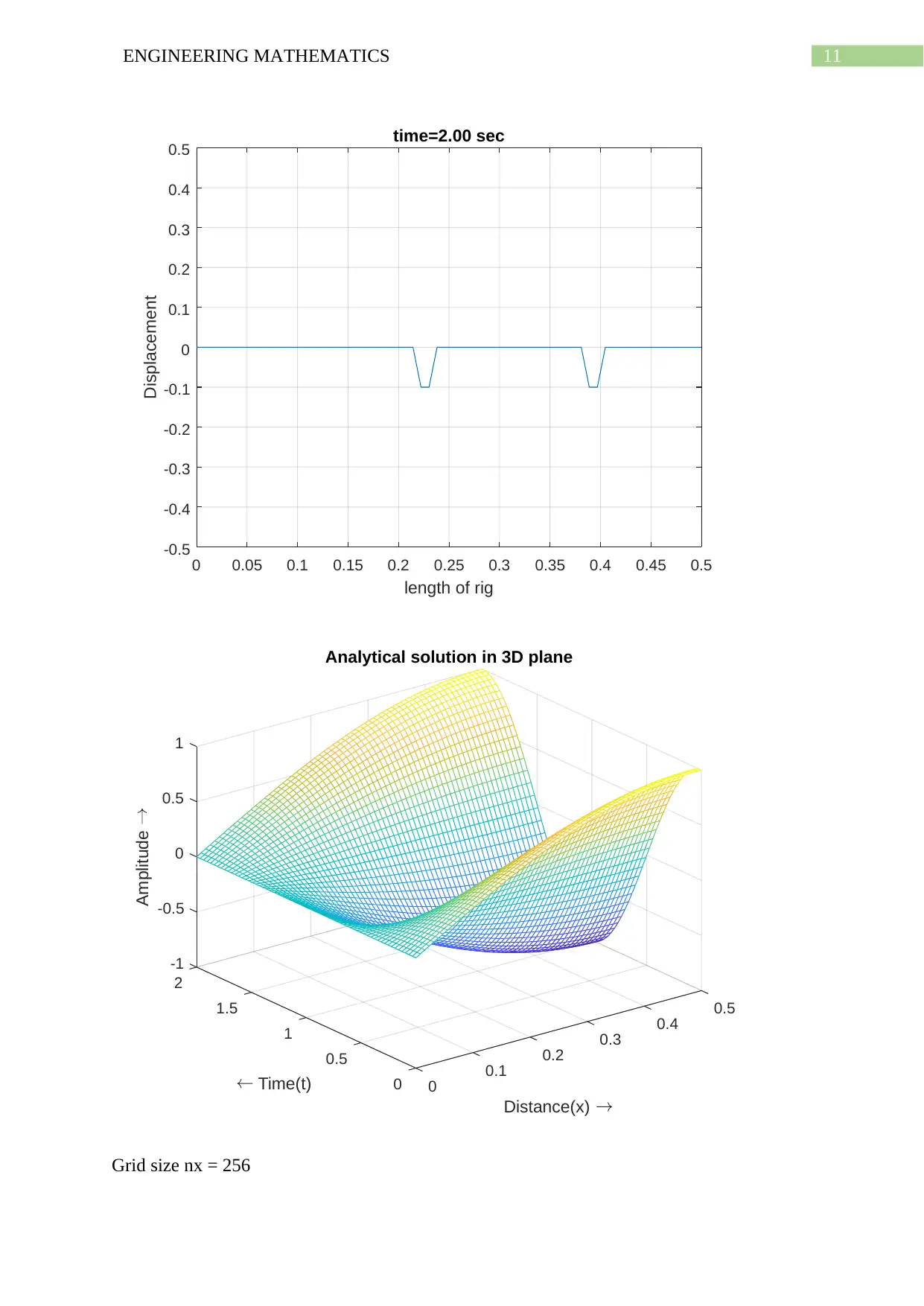
11ENGINEERING MATHEMATICS
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
length of rig
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Displacement
time=2.00 sec
-1
2
-0.5
1.5 0.5
0
Amplitude
0.4
Analytical solution in 3D plane
0.5
Time(t)
1 0.3
Distance(x)
1
0.20.5 0.1
0 0
Grid size nx = 256

12ENGINEERING MATHEMATICS
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
length of rig
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Displacement
time=2.00 sec

13ENGINEERING MATHEMATICS
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
length of rig [m]
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Displacement [m]
time=2.00 sec
Section 3:

14ENGINEERING MATHEMATICS
The forcing included governing wave equation is given by,
( ∂2
∂ t2 )u ( x , t ) – c2∗( ∂2
∂ x2 )u ( x , t ) = 1
ρ F( x , t)
Here, F(x,t) is the time varying force applied to each point in the web. The force function as
induced by the sonic wave inducer is given by,
Here, α1 = 0.5*10^(-2) force amplitude
f = 540 Hz.
λ = c/f the wavelength of the force
εt = fine tuning offset.
MATLAB code:
clc
clear
Lx = 0.5; % length of the test rig is 0.5 meters
dx = 0.01; % unit increment of displacemnt x
nx = 128; %grid size
x = linspace(0,Lx,nx);

15ENGINEERING MATHEMATICS
T= 3; % time for simulation is 5 secs
xn = zeros(nx,1); %
xnm1 = xn;
xnp1 = xn;
CFL = 1; % CFL number is 1
c = 1;
dt = CFL*dx/c; % c = CFL*(dx/dt)
% creating a disturbance or wave in the middle of the rig that will
% propagate
xn(24:26) = [0.1 0.2 0.1];
xnp1(:) = xn(:);
t=0; % staring time t=0
while t<T

16ENGINEERING MATHEMATICS
% Wave reflects from boundary
xn([1 end])=0;
t = t+dt;
xnm1 = xn;
xn = xnp1;
% defining paramters for the force function
alpha1 = 0.5e-2; epsilont = 0.8; f = 540; lambda = c/f;rho = 1e-4;
for i=2:nx-1
xn(i) = (1/rho)*alpha1*cos(epsilont*2*pi*f*t)*sin(2*pi*xn(i)/lambda);
xnp1(i) = 2*xn(i) - xnm1(i) + CFL^2*(xn(i+1) - 2*xn(i) + xn(i-1)); % implementing
discretized equation
end
clf;
plot(x,xn)
grid on

17ENGINEERING MATHEMATICS
title(sprintf('time=%.2f sec',t));
shg; pause(0.00001)
end
Output:
εt = 0.8:
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
length of rig [m]
-25
-20
-15
-10
-5
0
5
10
15
20
25
Displacement [m]
time=3.01 sec
When εt = 0.95:

18ENGINEERING MATHEMATICS
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
length of rig [m]
-40
-30
-20
-10
0
10
20
30
40
Displacement [m]
time=3.01 sec
When εt = 1:
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
length of rig [m]
-50
-40
-30
-20
-10
0
10
20
30
40
50
Displacement [m]
time=3.01 sec

19ENGINEERING MATHEMATICS