What are the expectations form developers and engineers?
VerifiedAdded on 2022/08/21
|10
|1871
|24
AI Summary
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Running head: ENGINEERING PRINCIPLES
ENGINEERING PRINCIPLES
Name of the Student
Name of the University
Author Note
ENGINEERING PRINCIPLES
Name of the Student
Name of the University
Author Note
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

1ENGINEERING PRINCIPLES
Title of the Experiment
Measurement of ‘g’ using a simple pendulum
Aim of the Experiment
To measure the acceleration due to gravity using a simple pendulum.
Gravity and Acceleration due to gravity
Gravity is a force of attraction acting between two matters in the universe. On other language
Gravity (Gravitation) is force by which the earth attracts other objects towards its center. Gravity
holds the satellite around planets, planets around the stars and stars in the galaxy (Caputo 2016).
It provide a balance between the matters. The mathematical expression for the force is given by,
F=ma
Gravitation force is directly proportional to the mass of the object and earth and inversely
proportional to the square of the distance between the object and center of the earth. Although it
is known that an object changes its velocity when force is applied. In the case of free falling or
vertical motion the velocity of the object increases (Gould 2016). The force supplied for this
increment is the gravitational force. The proportionality relationship can be given by,
Fg αMm & Fg α 1
r2
Here Fg is gravitational force, r is the distance between the object and center of the earth, M is
the mass of earth and m is the mass of the object.
Hence, the expression will be Fg α Mm
r2
Title of the Experiment
Measurement of ‘g’ using a simple pendulum
Aim of the Experiment
To measure the acceleration due to gravity using a simple pendulum.
Gravity and Acceleration due to gravity
Gravity is a force of attraction acting between two matters in the universe. On other language
Gravity (Gravitation) is force by which the earth attracts other objects towards its center. Gravity
holds the satellite around planets, planets around the stars and stars in the galaxy (Caputo 2016).
It provide a balance between the matters. The mathematical expression for the force is given by,
F=ma
Gravitation force is directly proportional to the mass of the object and earth and inversely
proportional to the square of the distance between the object and center of the earth. Although it
is known that an object changes its velocity when force is applied. In the case of free falling or
vertical motion the velocity of the object increases (Gould 2016). The force supplied for this
increment is the gravitational force. The proportionality relationship can be given by,
Fg αMm & Fg α 1
r2
Here Fg is gravitational force, r is the distance between the object and center of the earth, M is
the mass of earth and m is the mass of the object.
Hence, the expression will be Fg α Mm
r2

2ENGINEERING PRINCIPLES
=> Fg=G Mm
r2 [where G is the Universal gravitational constant]
This equation is known as Universal Gravitation Equation. It is defined that the gravity is a
universal force (Vayenas, Fokas and Grigoriou 2015). During free falling the velocity of the
object increases while it reaching to the ground. Using the newton second law, (f=ma) the
Universal gravitation Equation can be expressed as,
=>Fg=G Mm
r2
=>ma=G Mm
r2 [F=ma]
=>a=G M
r2
Hence, the above derived value of ‘a’ is the acceleration due to gravity. It does not depends on
the mass and the true value of the acceleration due to gravity is 9.81 Meter per Second Square. It
is denoted by ‘g’.
Apparatus
Thread: Thread is used to tie the pendulum to the stand and suspended freely.
Pendulum: Pendulum is used to provide a mass to the simple harmonic motion.
Ruler: ruler is used here the measure the lengths of the thread.
Stand: Stand supports the system.
Stopwatch: A stopwatch is used to record and observe time for the each 10 oscillations of the
bob.
=> Fg=G Mm
r2 [where G is the Universal gravitational constant]
This equation is known as Universal Gravitation Equation. It is defined that the gravity is a
universal force (Vayenas, Fokas and Grigoriou 2015). During free falling the velocity of the
object increases while it reaching to the ground. Using the newton second law, (f=ma) the
Universal gravitation Equation can be expressed as,
=>Fg=G Mm
r2
=>ma=G Mm
r2 [F=ma]
=>a=G M
r2
Hence, the above derived value of ‘a’ is the acceleration due to gravity. It does not depends on
the mass and the true value of the acceleration due to gravity is 9.81 Meter per Second Square. It
is denoted by ‘g’.
Apparatus
Thread: Thread is used to tie the pendulum to the stand and suspended freely.
Pendulum: Pendulum is used to provide a mass to the simple harmonic motion.
Ruler: ruler is used here the measure the lengths of the thread.
Stand: Stand supports the system.
Stopwatch: A stopwatch is used to record and observe time for the each 10 oscillations of the
bob.

3ENGINEERING PRINCIPLES
Figure 1: Diagram of Apparatus
Source: Created by author
Methodology Used
The methodology used for detecting the acceleration due to gravity is done with
experiment of a simple pendulum. Pendulums perform simple harmonic motion and its period is
given by an acceleration which is directly proportional to the displacement of the pendulum and
directed towards the center of the motion (Pili and Violanda 2018). The value of g can be
calculated using the newton’s gravitation law = Fg=G Mm
r2 and newton’s second law of motion
gives F=mg. Using these two equations the time period of a simple pendulum can be expressed
by,
T =2 π √ L
g [Here the T is time period, L is length of the thread and g is the
acceleration due to gravity]
Figure 1: Diagram of Apparatus
Source: Created by author
Methodology Used
The methodology used for detecting the acceleration due to gravity is done with
experiment of a simple pendulum. Pendulums perform simple harmonic motion and its period is
given by an acceleration which is directly proportional to the displacement of the pendulum and
directed towards the center of the motion (Pili and Violanda 2018). The value of g can be
calculated using the newton’s gravitation law = Fg=G Mm
r2 and newton’s second law of motion
gives F=mg. Using these two equations the time period of a simple pendulum can be expressed
by,
T =2 π √ L
g [Here the T is time period, L is length of the thread and g is the
acceleration due to gravity]
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

4ENGINEERING PRINCIPLES
Now squaring both sides,
=> T 2=4 π2 L
g
=> g¿ 4 π 2 L
T2
Using the above equation g can be calculated.
Procedure
i. Fix the small pendulum to the thread and fix the thread on the stand.
ii. Take measure for the length of the thread. (Neglecting the radius of the pendulum).
iii. Take time using a stopwatch for 10 oscillations.
iv. Then calculate the time period by dividing by it 10.
v. Repeat the experiment by varying the lengths of the thread.
vi. Lastly calculate the gravity due to acceleration using formula.
vii. Next calculate the error percentage of the calculation with respect to the true value of g.
Results
After the requirement analysis for the experiment, the experiment is carried out to find
the time taken for the 10 oscillations of the pendulum dropped from a certain place and changing
length of the string. The average of the time of the 10 oscillation will give the average time of the
10 oscillation. Next it is divided by ten to get the one period of the pendulum. Now the value of
4 ¿) L is calculated using the different length of the threads. Then the value of g is obtained by
the given formula. The below table represents the experimental data of the lab.
Now squaring both sides,
=> T 2=4 π2 L
g
=> g¿ 4 π 2 L
T2
Using the above equation g can be calculated.
Procedure
i. Fix the small pendulum to the thread and fix the thread on the stand.
ii. Take measure for the length of the thread. (Neglecting the radius of the pendulum).
iii. Take time using a stopwatch for 10 oscillations.
iv. Then calculate the time period by dividing by it 10.
v. Repeat the experiment by varying the lengths of the thread.
vi. Lastly calculate the gravity due to acceleration using formula.
vii. Next calculate the error percentage of the calculation with respect to the true value of g.
Results
After the requirement analysis for the experiment, the experiment is carried out to find
the time taken for the 10 oscillations of the pendulum dropped from a certain place and changing
length of the string. The average of the time of the 10 oscillation will give the average time of the
10 oscillation. Next it is divided by ten to get the one period of the pendulum. Now the value of
4 ¿) L is calculated using the different length of the threads. Then the value of g is obtained by
the given formula. The below table represents the experimental data of the lab.
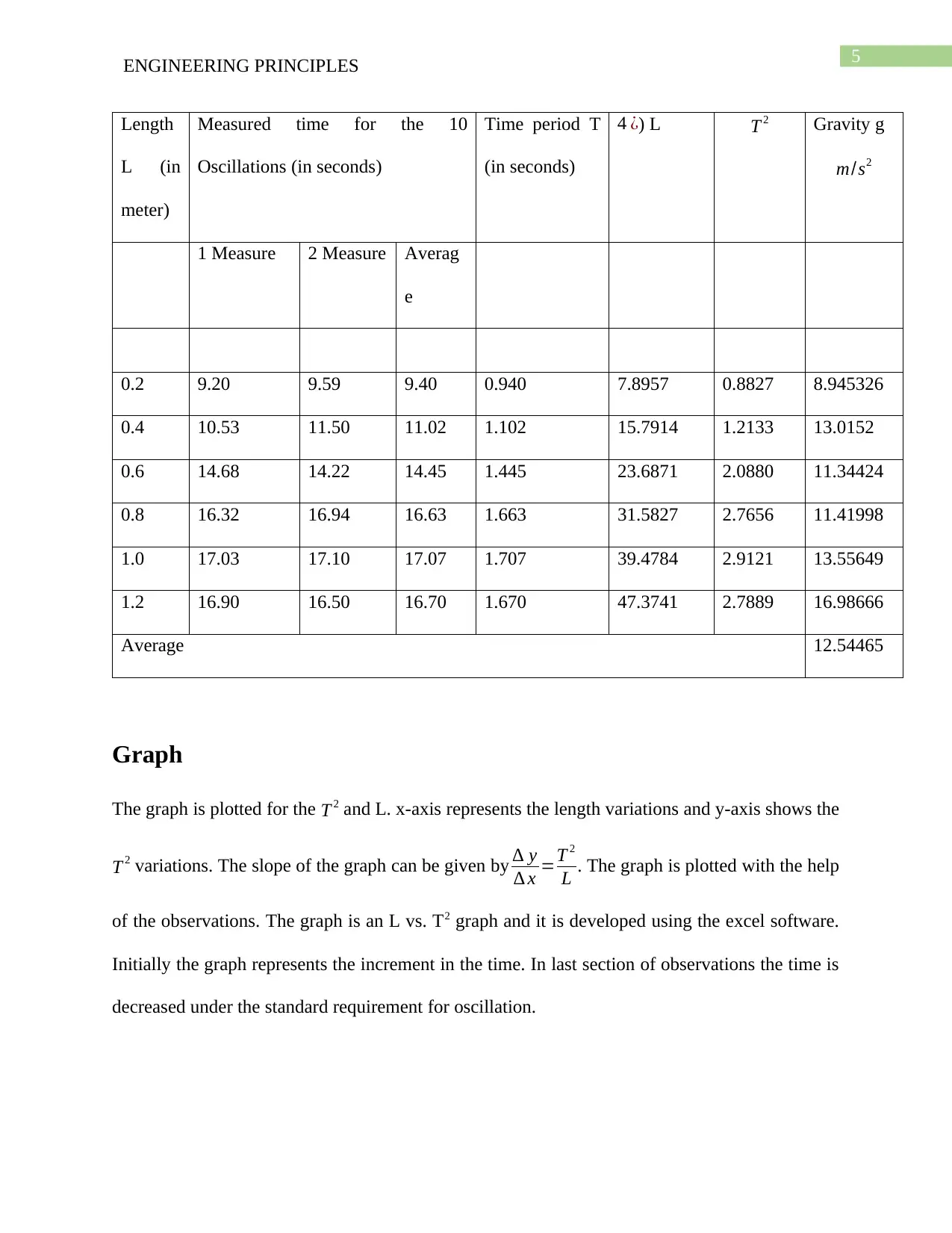
5ENGINEERING PRINCIPLES
Length
L (in
meter)
Measured time for the 10
Oscillations (in seconds)
Time period T
(in seconds)
4 ¿) L T 2 Gravity g
m/s2
1 Measure 2 Measure Averag
e
0.2 9.20 9.59 9.40 0.940 7.8957 0.8827 8.945326
0.4 10.53 11.50 11.02 1.102 15.7914 1.2133 13.0152
0.6 14.68 14.22 14.45 1.445 23.6871 2.0880 11.34424
0.8 16.32 16.94 16.63 1.663 31.5827 2.7656 11.41998
1.0 17.03 17.10 17.07 1.707 39.4784 2.9121 13.55649
1.2 16.90 16.50 16.70 1.670 47.3741 2.7889 16.98666
Average 12.54465
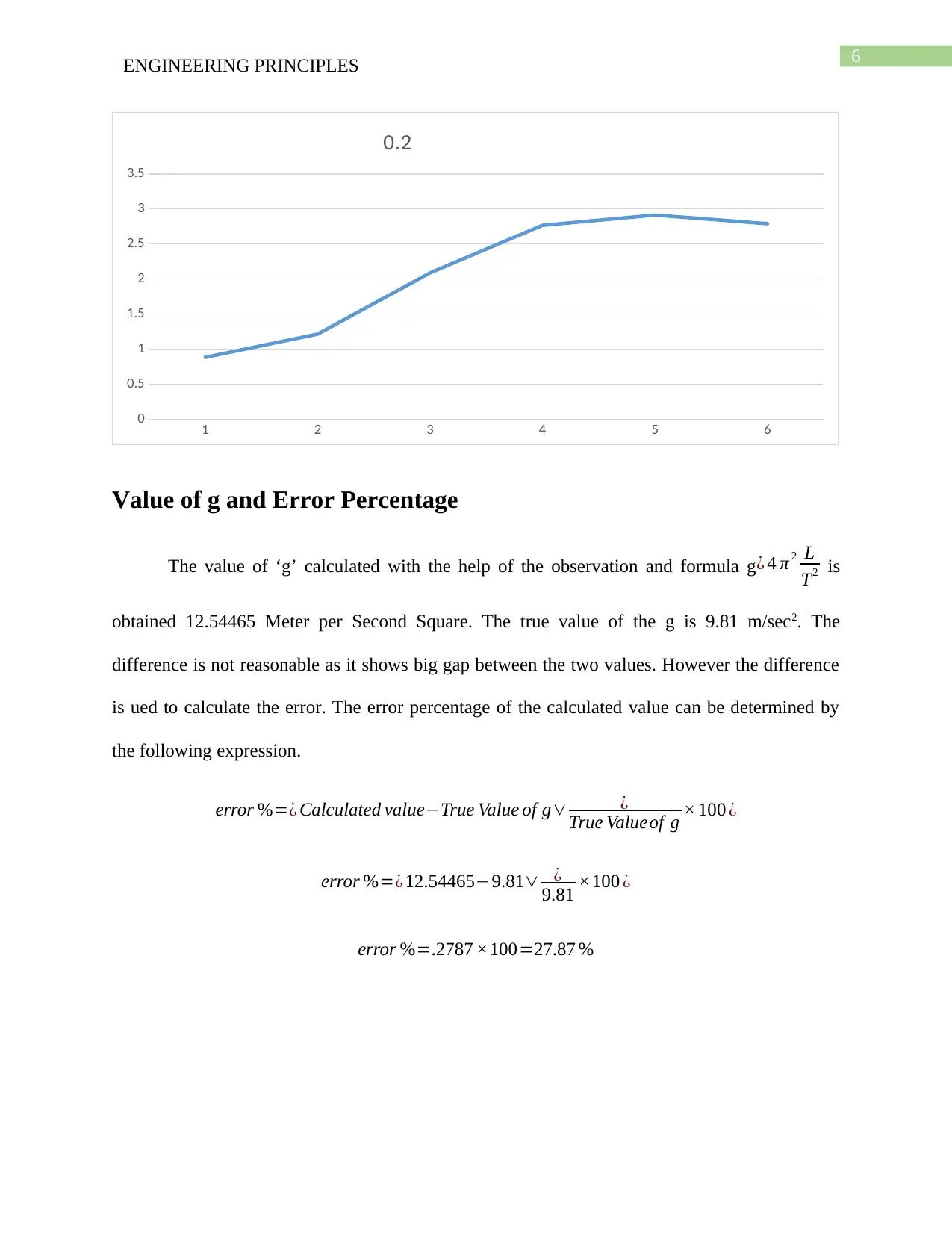
Graph
The graph is plotted for the T 2 and L. x-axis represents the length variations and y-axis shows the
T 2 variations. The slope of the graph can be given by ∆ y
∆ x =T 2
L . The graph is plotted with the help
of the observations. The graph is an L vs. T2 graph and it is developed using the excel software.
Initially the graph represents the increment in the time. In last section of observations the time is
decreased under the standard requirement for oscillation.
Length
L (in
meter)
Measured time for the 10
Oscillations (in seconds)
Time period T
(in seconds)
4 ¿) L T 2 Gravity g
m/s2
1 Measure 2 Measure Averag
e
0.2 9.20 9.59 9.40 0.940 7.8957 0.8827 8.945326
0.4 10.53 11.50 11.02 1.102 15.7914 1.2133 13.0152
0.6 14.68 14.22 14.45 1.445 23.6871 2.0880 11.34424
0.8 16.32 16.94 16.63 1.663 31.5827 2.7656 11.41998
1.0 17.03 17.10 17.07 1.707 39.4784 2.9121 13.55649
1.2 16.90 16.50 16.70 1.670 47.3741 2.7889 16.98666
Average 12.54465
Graph
The graph is plotted for the T 2 and L. x-axis represents the length variations and y-axis shows the
T 2 variations. The slope of the graph can be given by ∆ y
∆ x =T 2
L . The graph is plotted with the help
of the observations. The graph is an L vs. T2 graph and it is developed using the excel software.
Initially the graph represents the increment in the time. In last section of observations the time is
decreased under the standard requirement for oscillation.
6ENGINEERING PRINCIPLES
1 2 3 4 5 6
0
0.5
1
1.5
2
2.5
3
3.5
0.2
Value of g and Error Percentage
The value of ‘g’ calculated with the help of the observation and formula g¿ 4 π 2 L
T2 is
obtained 12.54465 Meter per Second Square. The true value of the g is 9.81 m/sec2. The
difference is not reasonable as it shows big gap between the two values. However the difference
is ued to calculate the error. The error percentage of the calculated value can be determined by
the following expression.
error %=¿ Calculated value−True Value of g∨ ¿
True Valueof g × 100 ¿
error %=¿ 12.54465−9.81∨ ¿
9.81 ×100 ¿
error %=.2787 ×100=27.87 %
1 2 3 4 5 6
0
0.5
1
1.5
2
2.5
3
3.5
0.2
Value of g and Error Percentage
The value of ‘g’ calculated with the help of the observation and formula g¿ 4 π 2 L
T2 is
obtained 12.54465 Meter per Second Square. The true value of the g is 9.81 m/sec2. The
difference is not reasonable as it shows big gap between the two values. However the difference
is ued to calculate the error. The error percentage of the calculated value can be determined by
the following expression.
error %=¿ Calculated value−True Value of g∨ ¿
True Valueof g × 100 ¿
error %=¿ 12.54465−9.81∨ ¿
9.81 ×100 ¿
error %=.2787 ×100=27.87 %
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

7ENGINEERING PRINCIPLES
Analysis and Discussion
The motion of the falling object is the result of the gravity between the object and earth. If the
friction force is neglected for the air while freely falling, then all the type of objects irrespective
size and mass, will accelerate with the same rate. The variation of the acceleration due to gravity
is also seen in the experiment which depends on the distance between the center of the earth and
the object (Iorio 2016). It is known that earth is flat at poles and wide at equator. Hence the
distance between the object and the earth will be less on poles and greater at the equator. On
other hand altitude of the object also affects the value of the gravity. From sea level to very
height of Mt. Everest the value of g is reduce by 0.28%. Similarly the depth of the object also
create different gravity.
In this experiment of finding the value of g, the calculation has given the value =
12.54465 m/s2. The error percentage of the value is 27% with the standard value of the ‘g’. The
accepted values for the time measurements are lower than the actual values which results in
higher acceleration rates at the end of the observations. The line in the graphs is supposed have a
constant line. Apart from that, it shows two curves on the line which represents the lower values
of Time.
Reasons for Uncertainties
1. Reasons for uncertainties could be neglecting the radius of the bob.
2. Pendulum represents simple harmonic motion and it may have been possible that any
deviation happened during the experiment. It can be seen as a main fact that the time periods
have been observed less than the required.
3. The role of friction is also present between thread-bob and thread-stand or the bob-air.
Analysis and Discussion
The motion of the falling object is the result of the gravity between the object and earth. If the
friction force is neglected for the air while freely falling, then all the type of objects irrespective
size and mass, will accelerate with the same rate. The variation of the acceleration due to gravity
is also seen in the experiment which depends on the distance between the center of the earth and
the object (Iorio 2016). It is known that earth is flat at poles and wide at equator. Hence the
distance between the object and the earth will be less on poles and greater at the equator. On
other hand altitude of the object also affects the value of the gravity. From sea level to very
height of Mt. Everest the value of g is reduce by 0.28%. Similarly the depth of the object also
create different gravity.
In this experiment of finding the value of g, the calculation has given the value =
12.54465 m/s2. The error percentage of the value is 27% with the standard value of the ‘g’. The
accepted values for the time measurements are lower than the actual values which results in
higher acceleration rates at the end of the observations. The line in the graphs is supposed have a
constant line. Apart from that, it shows two curves on the line which represents the lower values
of Time.
Reasons for Uncertainties
1. Reasons for uncertainties could be neglecting the radius of the bob.
2. Pendulum represents simple harmonic motion and it may have been possible that any
deviation happened during the experiment. It can be seen as a main fact that the time periods
have been observed less than the required.
3. The role of friction is also present between thread-bob and thread-stand or the bob-air.

8ENGINEERING PRINCIPLES
4. The angle from where the bob is dropped may have interfered with the observed data.
5. The value of ‘g’ around the earth is not same due the high land-low land places and oval
shape of the earth. However, the differentiation of value of ‘g’ is negligible.
6. The stand may have not been standing straight. This could be the reason of inconsistency in
the data.
Improvements
The apparatus used for the experiment was set up to perform the assessment. The
apparatus should be cross checked before start taking observations. The systematic error in the
calculation of the acceleration due to gravity can be improved by doing length measurements
better. The accurate measurements of the length, mass, and stopwatch should be taken in order to
achieve precisely close value. The radius of the pendulum should be added with the length of the
string. Then the formula will become g¿ 4 π 2 ( L+r )
T 2 .
In future photo gate should be used to measure the periods of the pendulum with high
accuracy. Using different metal bobs will also provide different results. Instead of doing 10
oscillations, 20 oscillations should be done to get close values. Lastly, it can be said the report
successfully covers the aim of the experiment, explained theories and methodology along with
the correct calculations (Afandi 2018). The observation skill needs to be improved in order to get
close the results in future.
4. The angle from where the bob is dropped may have interfered with the observed data.
5. The value of ‘g’ around the earth is not same due the high land-low land places and oval
shape of the earth. However, the differentiation of value of ‘g’ is negligible.
6. The stand may have not been standing straight. This could be the reason of inconsistency in
the data.
Improvements
The apparatus used for the experiment was set up to perform the assessment. The
apparatus should be cross checked before start taking observations. The systematic error in the
calculation of the acceleration due to gravity can be improved by doing length measurements
better. The accurate measurements of the length, mass, and stopwatch should be taken in order to
achieve precisely close value. The radius of the pendulum should be added with the length of the
string. Then the formula will become g¿ 4 π 2 ( L+r )
T 2 .
In future photo gate should be used to measure the periods of the pendulum with high
accuracy. Using different metal bobs will also provide different results. Instead of doing 10
oscillations, 20 oscillations should be done to get close values. Lastly, it can be said the report
successfully covers the aim of the experiment, explained theories and methodology along with
the correct calculations (Afandi 2018). The observation skill needs to be improved in order to get
close the results in future.

9ENGINEERING PRINCIPLES
References
Afandi, Z., 2018, April. Development of gravity acceleration measurement using simple
harmonic motion pendulum method based on digital technology and photogate sensor. In IOP
Conference Series: Materials Science and Engineering (Vol. 335, No. 1, p. 012064). IOP
Publishing.
Caputo, M., 2016. The Gravity Field of the Earth: From Classical and Modern Methods.
Elsevier.
Gould, R.R., 2016. Why does a ball fall?: A new visualization for Einstein's model of
gravity. American Journal of Physics, 84(5), pp.396-402.
Iorio, L., 2016. Does Newton’s gravitational constant vary sinusoidally with time? Orbital
motions say no. Classical and Quantum Gravity, 33(4), p.045004.
Pili, U. and Violanda, R., 2018. A simple pendulum-based measurement of g with a smartphone
light sensor. Physics Education, 53(4), p.043001.
Vayenas, C.G., Fokas, A. and Grigoriou, D., 2015. Gravitational mass and Newton's universal
gravitational law under relativistic conditions. In Journal of Physics: Conference Series (Vol.
633, No. 1, p. 012033). IOP Publishing.
References
Afandi, Z., 2018, April. Development of gravity acceleration measurement using simple
harmonic motion pendulum method based on digital technology and photogate sensor. In IOP
Conference Series: Materials Science and Engineering (Vol. 335, No. 1, p. 012064). IOP
Publishing.
Caputo, M., 2016. The Gravity Field of the Earth: From Classical and Modern Methods.
Elsevier.
Gould, R.R., 2016. Why does a ball fall?: A new visualization for Einstein's model of
gravity. American Journal of Physics, 84(5), pp.396-402.
Iorio, L., 2016. Does Newton’s gravitational constant vary sinusoidally with time? Orbital
motions say no. Classical and Quantum Gravity, 33(4), p.045004.
Pili, U. and Violanda, R., 2018. A simple pendulum-based measurement of g with a smartphone
light sensor. Physics Education, 53(4), p.043001.
Vayenas, C.G., Fokas, A. and Grigoriou, D., 2015. Gravitational mass and Newton's universal
gravitational law under relativistic conditions. In Journal of Physics: Conference Series (Vol.
633, No. 1, p. 012033). IOP Publishing.
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





