Detailed Report on UK Station Data Analysis Over a 10-Year Period
VerifiedAdded on 2021/02/21
|9
|1407
|21
Report
AI Summary
This report presents a comprehensive analysis of passenger entry and exit data for a UK station over a 10-year period. It begins with a tabular presentation of the raw data, followed by graphical representations using pie and bar charts to facilitate quick understanding. The core of the report focuses on statistical analysis, calculating and interpreting the mean, median, mode, range, and standard deviation of the data. Furthermore, the report delves into the application of a linear forecasting model, outlining the steps involved in calculating the slope (m) and intercept (c) to predict future trends. The report concludes with forecasting estimations for the 12th and 15th years, providing valuable insights into potential passenger demand. References to relevant books and online resources are included to support the analysis.

Individual report
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Table of Contents
INTRODUCTION...........................................................................................................................1
1. The presentation of last 10 year data of the station.................................................................1
2. Presentation of the data in different graph .............................................................................2
3. Calculation of Mean, Median, Mode, standard deviation and range......................................3
4. Linear forecasting model ........................................................................................................4
CONCLUSION................................................................................................................................6
REFERENCES................................................................................................................................7
INTRODUCTION...........................................................................................................................1
1. The presentation of last 10 year data of the station.................................................................1
2. Presentation of the data in different graph .............................................................................2
3. Calculation of Mean, Median, Mode, standard deviation and range......................................3
4. Linear forecasting model ........................................................................................................4
CONCLUSION................................................................................................................................6
REFERENCES................................................................................................................................7
INTRODUCTION
The report highlight the data of last 10 year of the station. It explain the total no. of entry and exit
of the customer in last 10 in UK of the particular station. It present the data in the table form to
get the quick review of the last 10 year data and it also present the data in graph form so it can
easily understood. It highlights the usage of mean, median, mode, range and standard deviation
in the organisation and their usage in the data analyse. It also help to understand the meaning of
linear forecasting model in the organisation and the various steps to calculate the linear
forecasting for the 12 and 15 year. Linear forecasting model is use to predict the demand of the
trains with the time series by the passengers.
1. The presentation of last 10 year data of the station
Station
2008 10
2009 208
2010 57
2011 30
2012 54
2013 55
2014 59
2015 116
2016 232
2017 234
The above table represent the total number of entry and exit of the passenger in last 10
year of station in United Kingdom.
1
The report highlight the data of last 10 year of the station. It explain the total no. of entry and exit
of the customer in last 10 in UK of the particular station. It present the data in the table form to
get the quick review of the last 10 year data and it also present the data in graph form so it can
easily understood. It highlights the usage of mean, median, mode, range and standard deviation
in the organisation and their usage in the data analyse. It also help to understand the meaning of
linear forecasting model in the organisation and the various steps to calculate the linear
forecasting for the 12 and 15 year. Linear forecasting model is use to predict the demand of the
trains with the time series by the passengers.
1. The presentation of last 10 year data of the station
Station
2008 10
2009 208
2010 57
2011 30
2012 54
2013 55
2014 59
2015 116
2016 232
2017 234
The above table represent the total number of entry and exit of the passenger in last 10
year of station in United Kingdom.
1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
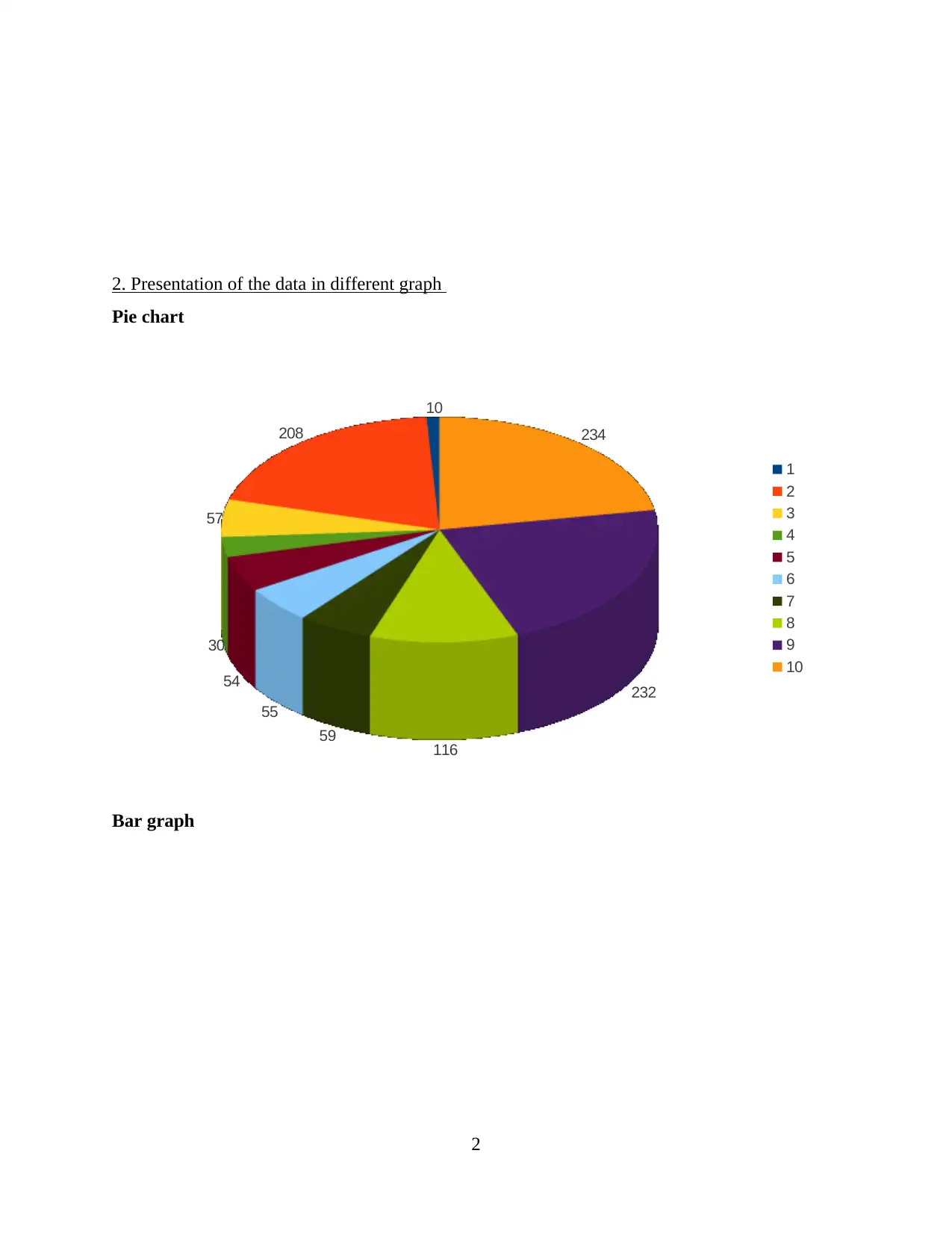
2. Presentation of the data in different graph
Pie chart
10
208
57
30
54
55
59 116
232
234
1
2
3
4
5
6
7
8
9
10
Bar graph
2
Pie chart
10
208
57
30
54
55
59 116
232
234
1
2
3
4
5
6
7
8
9
10
Bar graph
2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
1 2 3 4 5 6 7 8 9 10
0
50
100
150
200
250
Column C
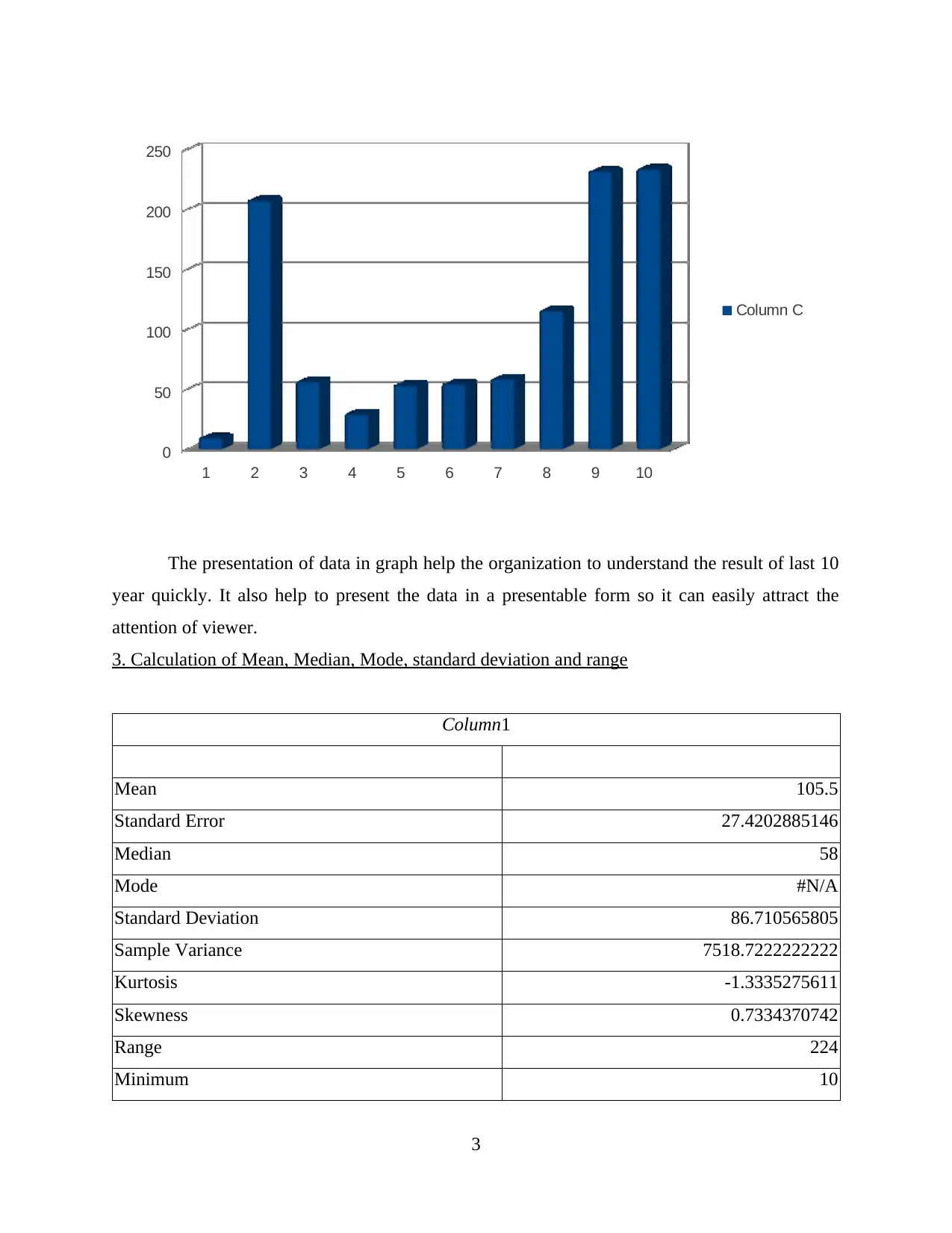
The presentation of data in graph help the organization to understand the result of last 10
year quickly. It also help to present the data in a presentable form so it can easily attract the
attention of viewer.
3. Calculation of Mean, Median, Mode, standard deviation and range
Column1
Mean 105.5
Standard Error 27.4202885146
Median 58
Mode #N/A
Standard Deviation 86.710565805
Sample Variance 7518.7222222222
Kurtosis -1.3335275611
Skewness 0.7334370742
Range 224
Minimum 10
3
0
50
100
150
200
250
Column C
The presentation of data in graph help the organization to understand the result of last 10
year quickly. It also help to present the data in a presentable form so it can easily attract the
attention of viewer.
3. Calculation of Mean, Median, Mode, standard deviation and range
Column1
Mean 105.5
Standard Error 27.4202885146
Median 58
Mode #N/A
Standard Deviation 86.710565805
Sample Variance 7518.7222222222
Kurtosis -1.3335275611
Skewness 0.7334370742
Range 224
Minimum 10
3
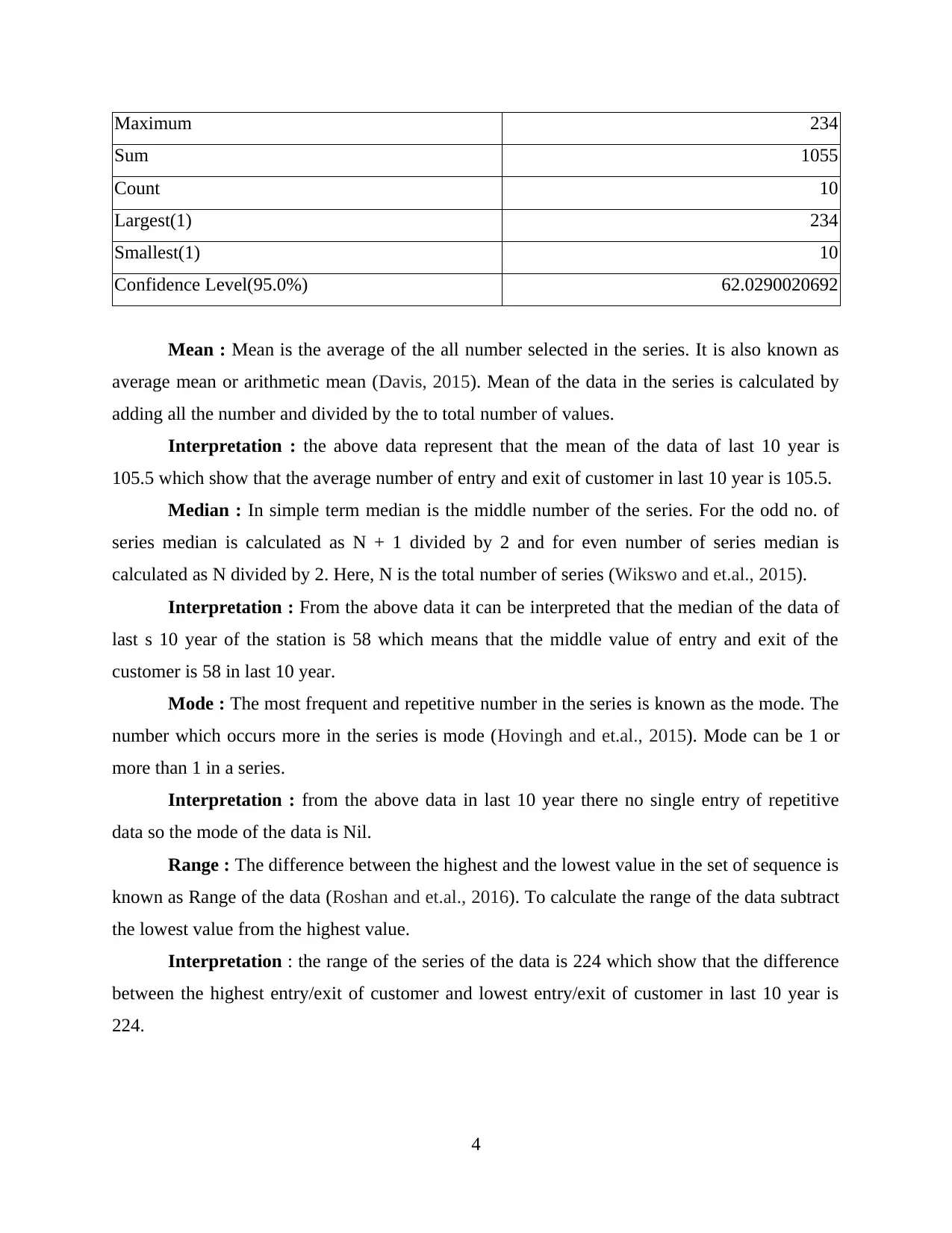
Maximum 234
Sum 1055
Count 10
Largest(1) 234
Smallest(1) 10
Confidence Level(95.0%) 62.0290020692
Mean : Mean is the average of the all number selected in the series. It is also known as
average mean or arithmetic mean (Davis, 2015). Mean of the data in the series is calculated by
adding all the number and divided by the to total number of values.
Interpretation : the above data represent that the mean of the data of last 10 year is
105.5 which show that the average number of entry and exit of customer in last 10 year is 105.5.
Median : In simple term median is the middle number of the series. For the odd no. of
series median is calculated as N + 1 divided by 2 and for even number of series median is
calculated as N divided by 2. Here, N is the total number of series (Wikswo and et.al., 2015).
Interpretation : From the above data it can be interpreted that the median of the data of
last s 10 year of the station is 58 which means that the middle value of entry and exit of the
customer is 58 in last 10 year.
Mode : The most frequent and repetitive number in the series is known as the mode. The
number which occurs more in the series is mode (Hovingh and et.al., 2015). Mode can be 1 or
more than 1 in a series.
Interpretation : from the above data in last 10 year there no single entry of repetitive
data so the mode of the data is Nil.
Range : The difference between the highest and the lowest value in the set of sequence is
known as Range of the data (Roshan and et.al., 2016). To calculate the range of the data subtract
the lowest value from the highest value.
Interpretation : the range of the series of the data is 224 which show that the difference
between the highest entry/exit of customer and lowest entry/exit of customer in last 10 year is
224.
4
Sum 1055
Count 10
Largest(1) 234
Smallest(1) 10
Confidence Level(95.0%) 62.0290020692
Mean : Mean is the average of the all number selected in the series. It is also known as
average mean or arithmetic mean (Davis, 2015). Mean of the data in the series is calculated by
adding all the number and divided by the to total number of values.
Interpretation : the above data represent that the mean of the data of last 10 year is
105.5 which show that the average number of entry and exit of customer in last 10 year is 105.5.
Median : In simple term median is the middle number of the series. For the odd no. of
series median is calculated as N + 1 divided by 2 and for even number of series median is
calculated as N divided by 2. Here, N is the total number of series (Wikswo and et.al., 2015).
Interpretation : From the above data it can be interpreted that the median of the data of
last s 10 year of the station is 58 which means that the middle value of entry and exit of the
customer is 58 in last 10 year.
Mode : The most frequent and repetitive number in the series is known as the mode. The
number which occurs more in the series is mode (Hovingh and et.al., 2015). Mode can be 1 or
more than 1 in a series.
Interpretation : from the above data in last 10 year there no single entry of repetitive
data so the mode of the data is Nil.
Range : The difference between the highest and the lowest value in the set of sequence is
known as Range of the data (Roshan and et.al., 2016). To calculate the range of the data subtract
the lowest value from the highest value.
Interpretation : the range of the series of the data is 224 which show that the difference
between the highest entry/exit of customer and lowest entry/exit of customer in last 10 year is
224.
4
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Standard deviation : Standard deviation is used to measure the variation of data from
the mean. The more variation represent the higher standard deviation and less variation represent
the lower standard deviation.
Interpretation : The standard deviation of the above data is 86.71 of last 10 year data of
entry and exit of the customer which means that the variation from the mean of the data is 86.71
(approx).
4. Linear forecasting model
Steps for calculating the linear forecasting model
Y = mX + c
Steps for calculating the value of M
In linear forecasting model the m is used to determine the slope of the data of last 10 year (A
linear forecasting model and its application to economic data, 2019). It can be calculated as :
m = NΣXY – ΣX ΣY / NΣX^2 – (ΣX)^2
Steps for calculating the value of c are :
c = ΣY – m ΣX / N
The indicators of forecasting the value for the 12 and 15 years are :
No. of years (X) Data (Y) XY X^2
1 10 10 1
2 208 416 4
3 57 171 9
4 30 120 16
5 54 270 25
6 55 330 36
7 59 413 49
8 116 928 64
9 232 2088 81
10 234 2340 100
55 1055 7086 385
m = NΣXY – ΣX ΣY / NΣX^2 – (ΣX)^2
5
the mean. The more variation represent the higher standard deviation and less variation represent
the lower standard deviation.
Interpretation : The standard deviation of the above data is 86.71 of last 10 year data of
entry and exit of the customer which means that the variation from the mean of the data is 86.71
(approx).
4. Linear forecasting model
Steps for calculating the linear forecasting model
Y = mX + c
Steps for calculating the value of M
In linear forecasting model the m is used to determine the slope of the data of last 10 year (A
linear forecasting model and its application to economic data, 2019). It can be calculated as :
m = NΣXY – ΣX ΣY / NΣX^2 – (ΣX)^2
Steps for calculating the value of c are :
c = ΣY – m ΣX / N
The indicators of forecasting the value for the 12 and 15 years are :
No. of years (X) Data (Y) XY X^2
1 10 10 1
2 208 416 4
3 57 171 9
4 30 120 16
5 54 270 25
6 55 330 36
7 59 413 49
8 116 928 64
9 232 2088 81
10 234 2340 100
55 1055 7086 385
m = NΣXY – ΣX ΣY / NΣX^2 – (ΣX)^2
5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

n = 10
ΣXY = 7086
ΣX = 55
ΣY = 1055
ΣX^2 = 385
m = 10*7086 – 55*1055 / 10*358 – (55)^2
= 12835 / 561
= 22.88
c = ΣY – m ΣX / N
ΣY = 1055
m = 22.88
ΣX = 55
N = 10
c = 1055 – 22.88*55 / 10
= -22.34
Forecasting linear model for 12 year :
Y = mX + c
X = 12
= 22.88*12 + (- 22.34)
= 252.22
Forecasting linear model for 15 year :
Y = mX + c
X = 15
= 22.88*15 + (- 22.34)
= 320.86
CONCLUSION
The above report summarize the presentation of data of entry and exit of the passenger of
last 10 year. The report help to understand the use of mean, median, mode, range and standard-
deviation in the organization and their application in the organization. It also help to understand
the usage of linear forecasting model and the ways to calculate the linear forecasting.
6
ΣXY = 7086
ΣX = 55
ΣY = 1055
ΣX^2 = 385
m = 10*7086 – 55*1055 / 10*358 – (55)^2
= 12835 / 561
= 22.88
c = ΣY – m ΣX / N
ΣY = 1055
m = 22.88
ΣX = 55
N = 10
c = 1055 – 22.88*55 / 10
= -22.34
Forecasting linear model for 12 year :
Y = mX + c
X = 12
= 22.88*12 + (- 22.34)
= 252.22
Forecasting linear model for 15 year :
Y = mX + c
X = 15
= 22.88*15 + (- 22.34)
= 320.86
CONCLUSION
The above report summarize the presentation of data of entry and exit of the passenger of
last 10 year. The report help to understand the use of mean, median, mode, range and standard-
deviation in the organization and their application in the organization. It also help to understand
the usage of linear forecasting model and the ways to calculate the linear forecasting.
6

REFERENCES
Books and Journals
Davis, J., 2015. Know your median from your mean and mode. Primary Teacher
Update, 2015(43). pp.35-36.
Hovingh, G.K., and et.al., 2015. The effect of an apolipoprotein AI–containing high-density
lipoprotein–mimetic particle (CER-001) on carotid artery wall thickness in patients with
7
Books and Journals
Davis, J., 2015. Know your median from your mean and mode. Primary Teacher
Update, 2015(43). pp.35-36.
Hovingh, G.K., and et.al., 2015. The effect of an apolipoprotein AI–containing high-density
lipoprotein–mimetic particle (CER-001) on carotid artery wall thickness in patients with
7
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





