Detailed Solutions for Algebraic Equations and Graphing Tasks
VerifiedAdded on 2023/05/27
|14
|968
|166
Homework Assignment
AI Summary
This document provides detailed solutions to a series of algebra problems involving linear and quadratic equations, as well as polynomial curves. The solutions include analyzing the order of equations, graphing functions, and exploring how changes in coefficients and constants affect the shape and position of the graphs. Tasks cover topics such as linear equations with varying slopes and intercepts, quadratic equations with different coefficients, and factorization of polynomial expressions to find x-intercepts. The analysis includes observations on how increasing or decreasing coefficients impacts the curves and their positions on the coordinate plane, with specific examples provided for each task. The final task involves analyzing a degree 5 polynomial curve and identifying its key features, such as intercepts and inflection points. Desklib offers this assignment solution to aid students in understanding and mastering algebraic concepts.
1 out of 14
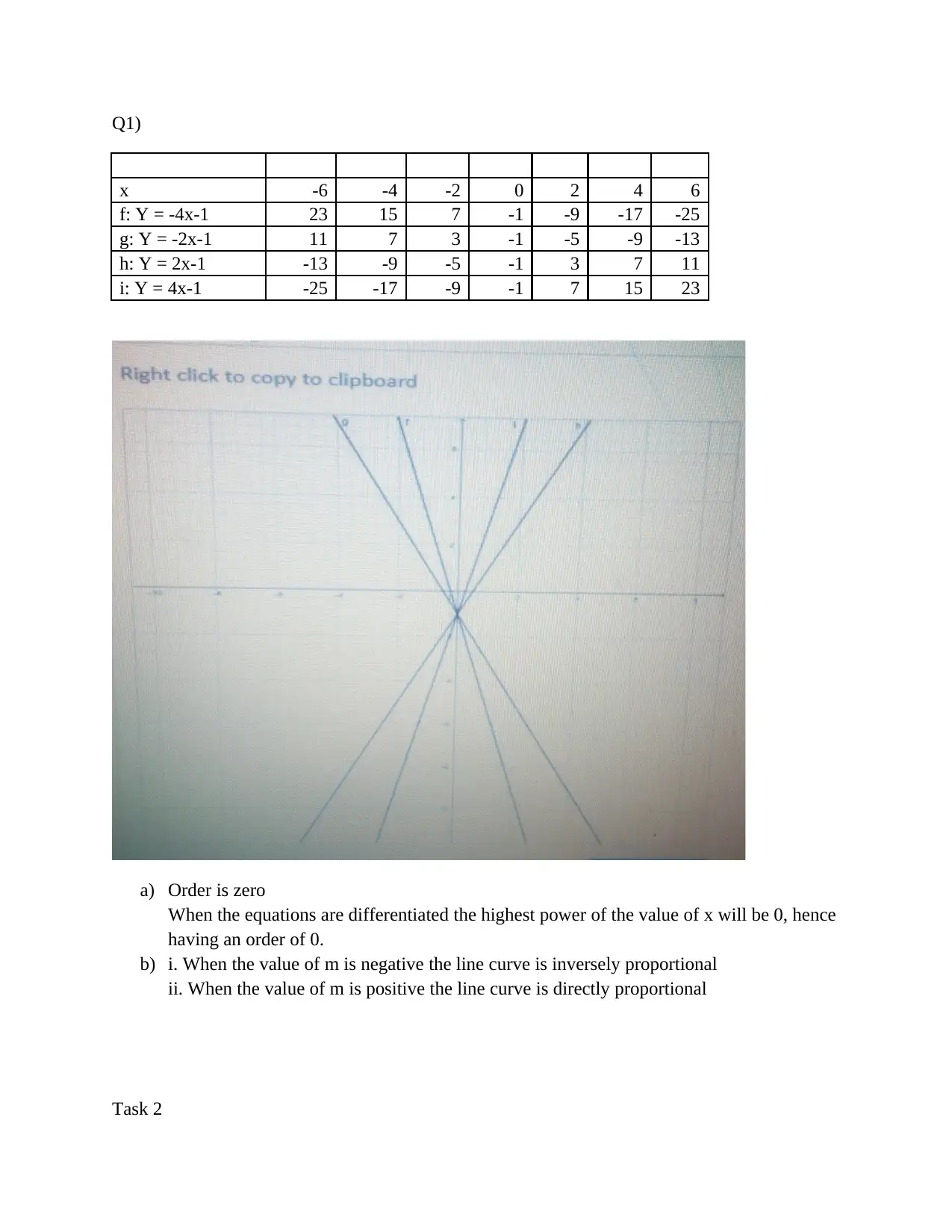
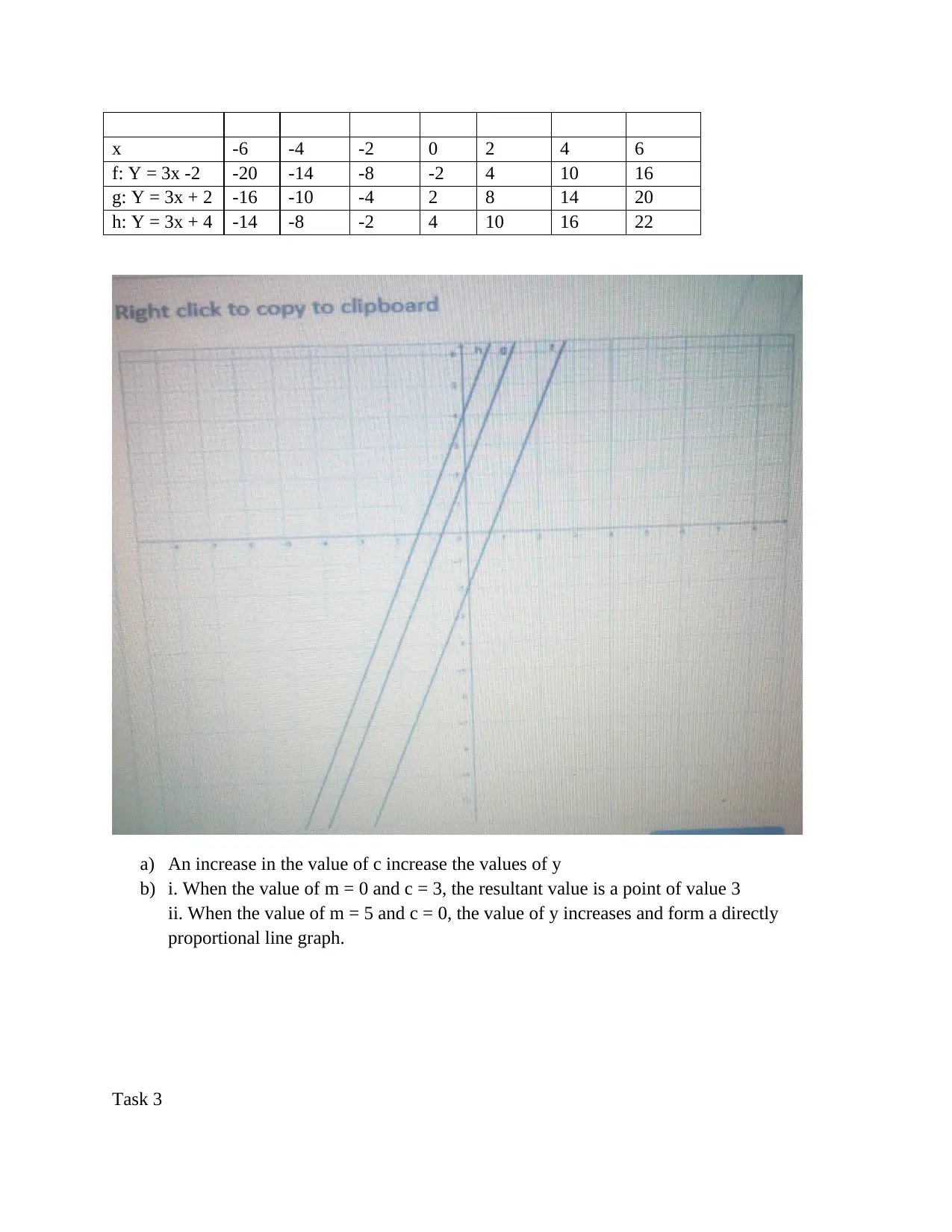
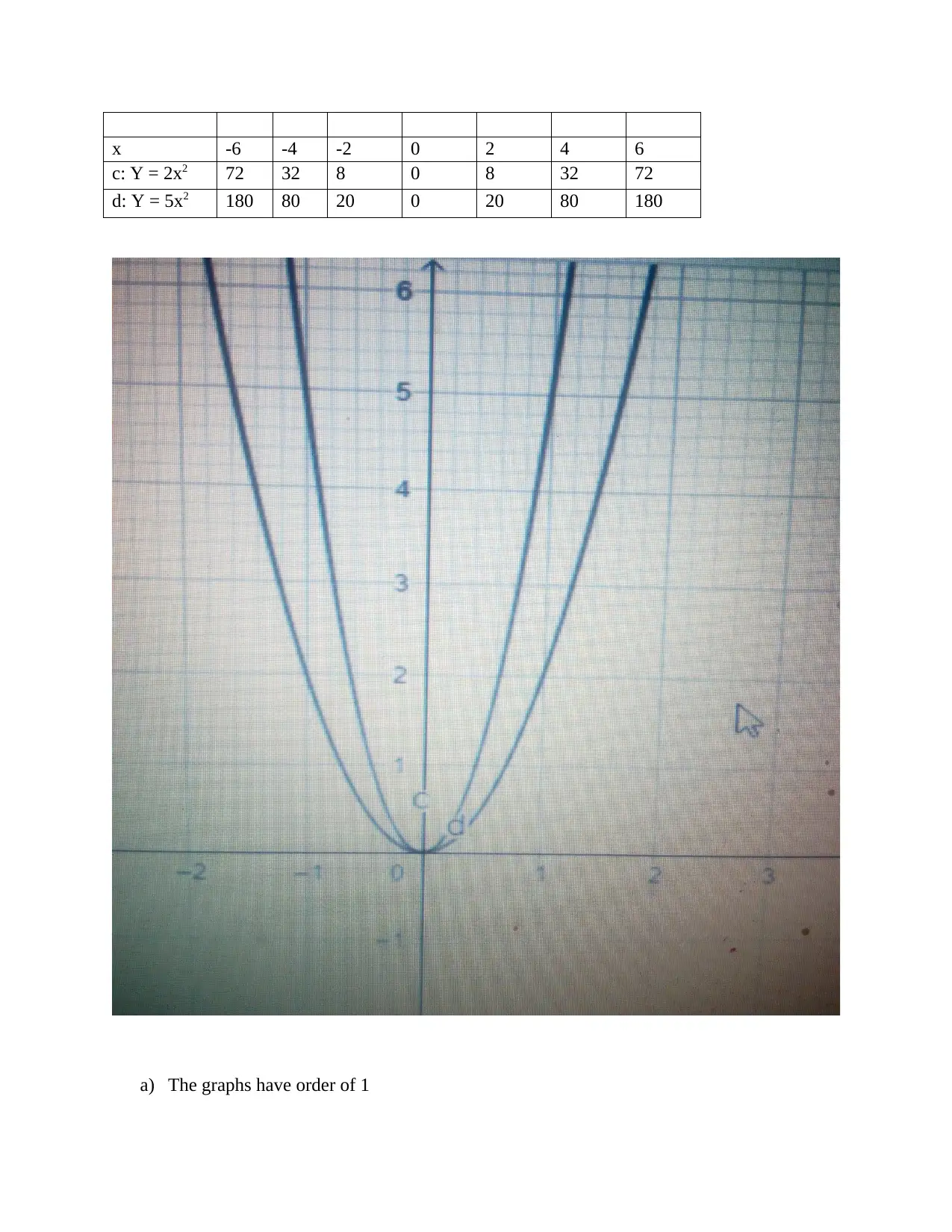

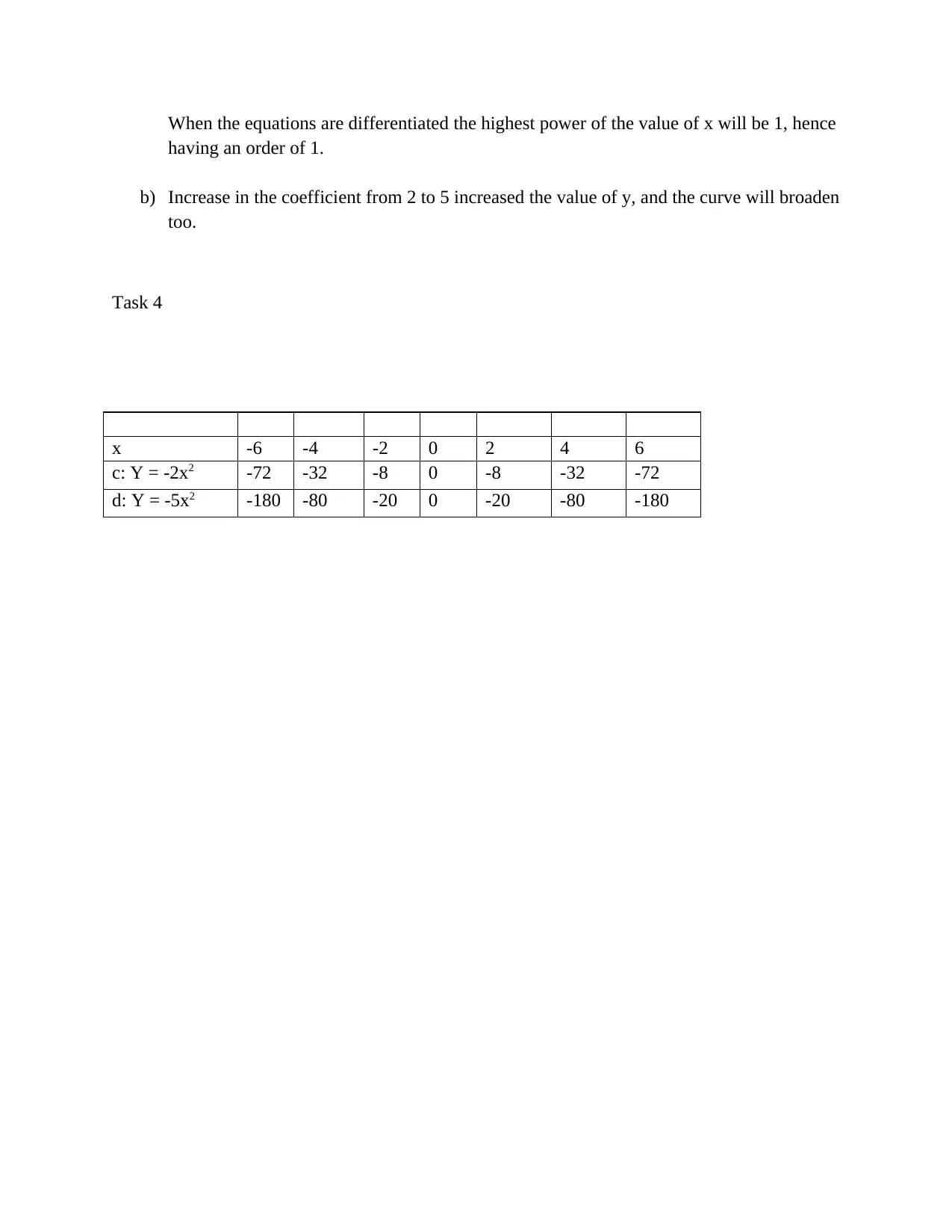



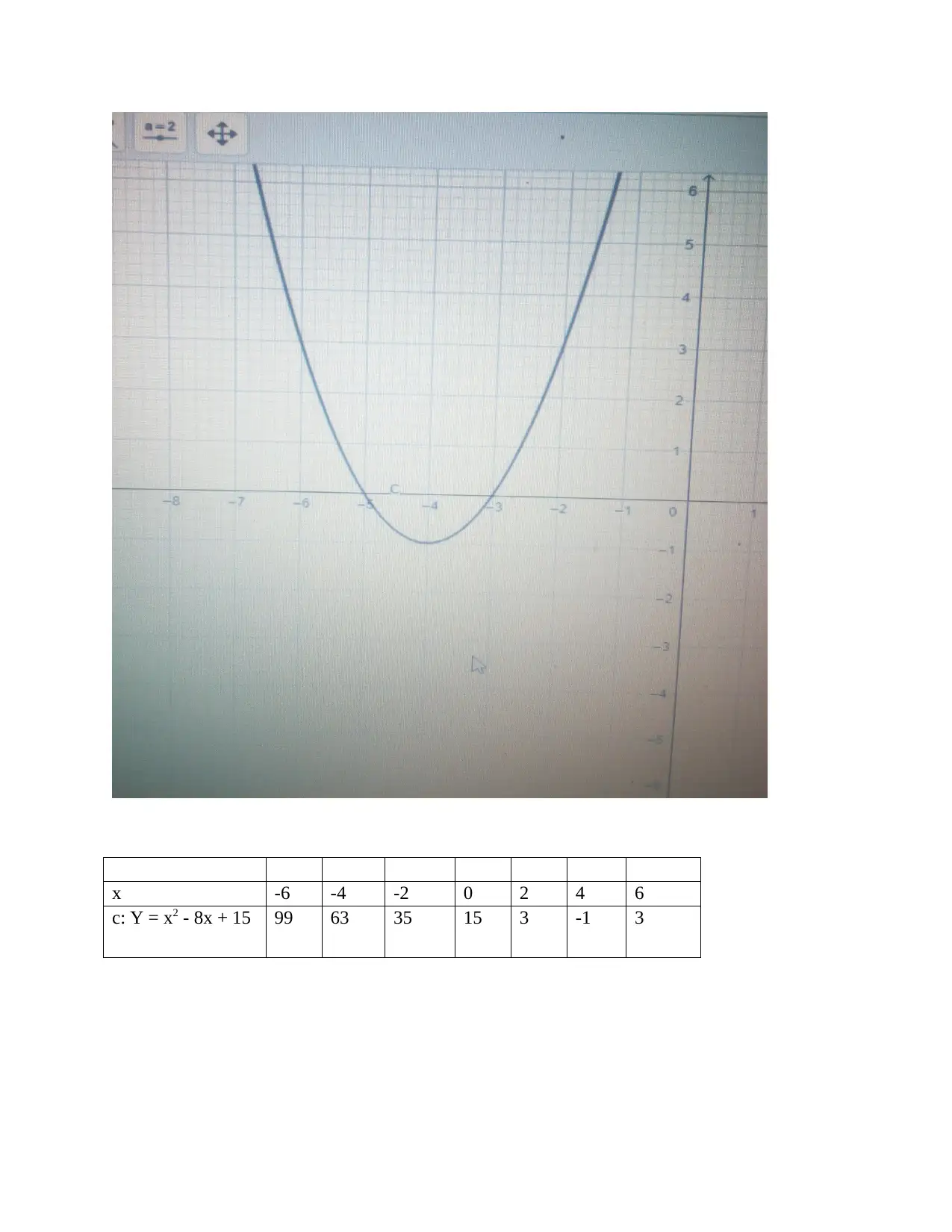
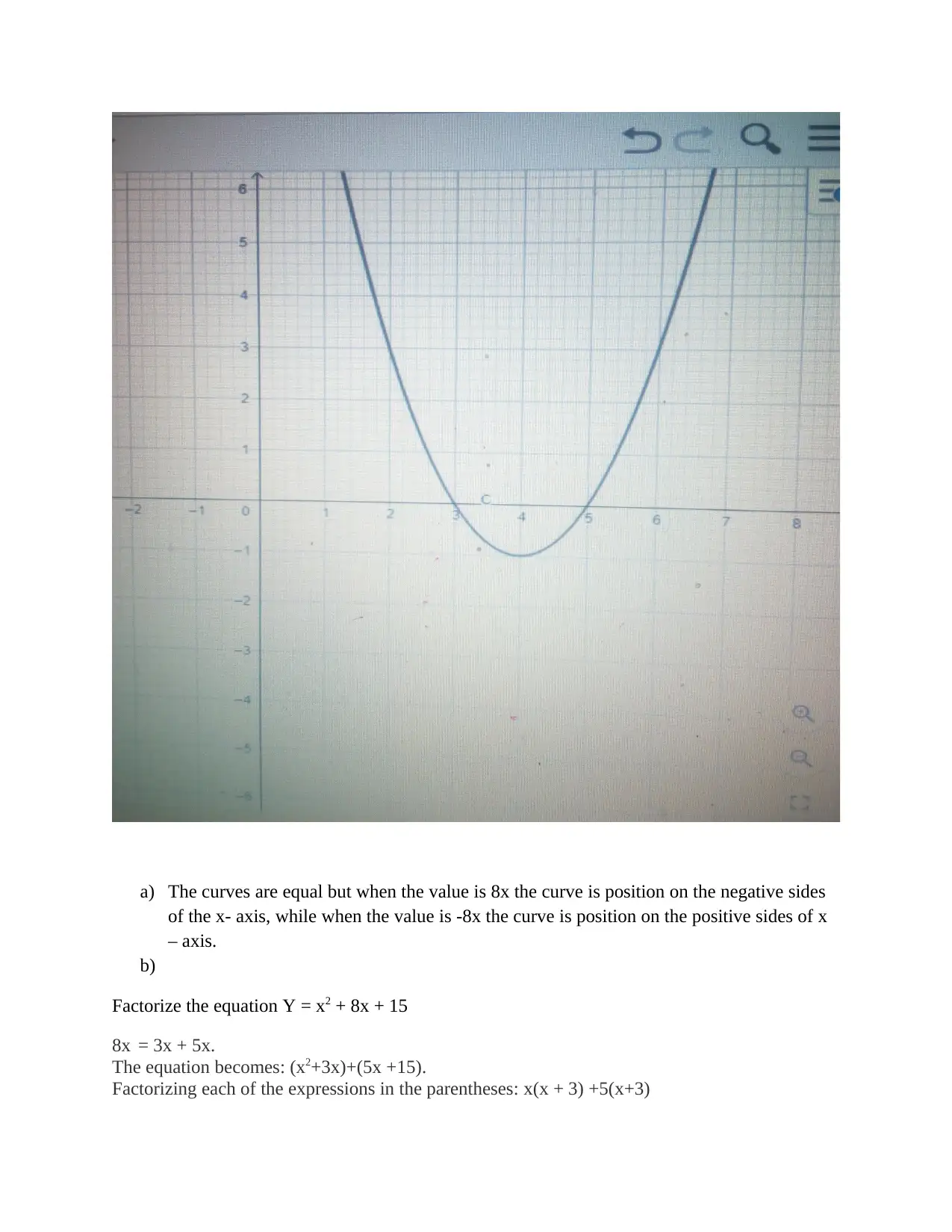

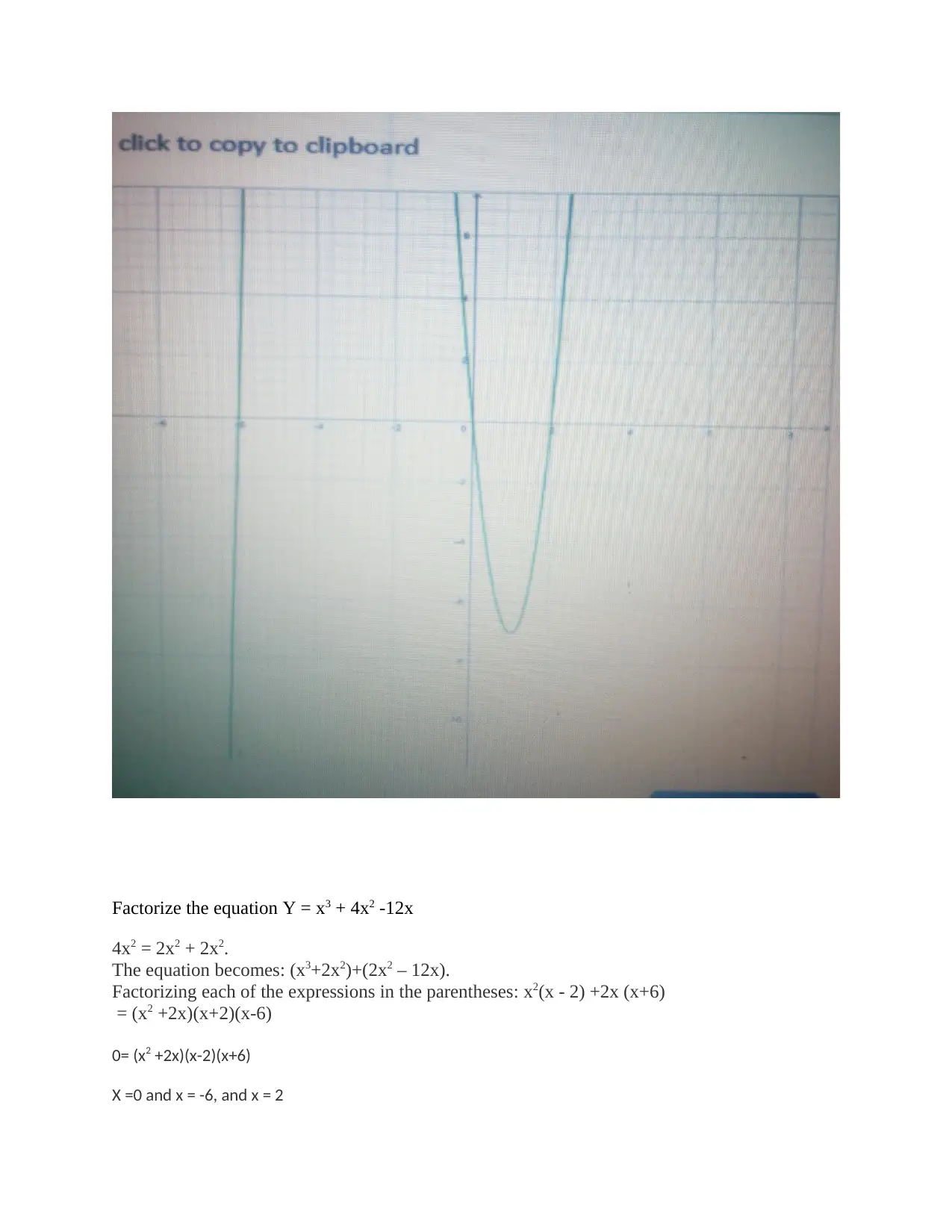







![[object Object]](/_next/static/media/star-bottom.7253800d.svg)