EDU10447 S1 2018: Environmental Assessment and Cricket Chirps
VerifiedAdded on 2023/06/11
|10
|1507
|149
Homework Assignment
AI Summary
This assignment solution involves statistical analysis across three distinct problems. The first problem focuses on estimating the surface area of two sites for an environmental impact assessment. The second problem explores the relationship between cricket chirp rates and temperature, using regression analysis to develop predictive models for two cricket species, including hypothesis testing and calculating chirp rates at specific temperatures. The third problem compares the Olympic medal tallies of Australia and Great Britain since World War II, using descriptive statistics and a two-sample t-test to determine which nation has demonstrated more consistent performance over time. The solutions include detailed calculations, interpretations of statistical results, and discussions of the real-world relevance and limitations of the analyses.

Question 1 ESTIMATING AREA 15% out of 45%
A local council surveyor is part of an environmental impact assessment team investigating possible
residential development of two areas of land. The surveyor must determine if the two areas, Site 1
and Site 2, which run along existing creeks and roads, are the same surface area.
The aim of this section was to estimate the real surface area of the two sites.
The computations are presented below;
Area of site 1:
( 6∗13 ) + 1
2 ( 7∗6 ) + ( 1.5∗6 )=78+21+ 9=108 cm2
But 1 cm2 represents 16 km2
So the real area would be;
108 cm2∗16 km2
1 cm2 =1728 km2
Area of site 2:
( 2∗11 )+ 1
2 ( 11∗6 ) + ( 3∗12 )=22+33+36=91 cm2
But 1 cm2 represents 16 km2
So the real area would be;
91 cm2∗16 km2
1 cm2 =1456 km2
Site 1
Driveway
A local council surveyor is part of an environmental impact assessment team investigating possible
residential development of two areas of land. The surveyor must determine if the two areas, Site 1
and Site 2, which run along existing creeks and roads, are the same surface area.
The aim of this section was to estimate the real surface area of the two sites.
The computations are presented below;
Area of site 1:
( 6∗13 ) + 1
2 ( 7∗6 ) + ( 1.5∗6 )=78+21+ 9=108 cm2
But 1 cm2 represents 16 km2
So the real area would be;
108 cm2∗16 km2
1 cm2 =1728 km2
Area of site 2:
( 2∗11 )+ 1
2 ( 11∗6 ) + ( 3∗12 )=22+33+36=91 cm2
But 1 cm2 represents 16 km2
So the real area would be;
91 cm2∗16 km2
1 cm2 =1456 km2
Site 1
Driveway
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Scale 1: 40 000
River
Farm Fence
Road
South Boundary
River
Farm Fence
Road
South Boundary
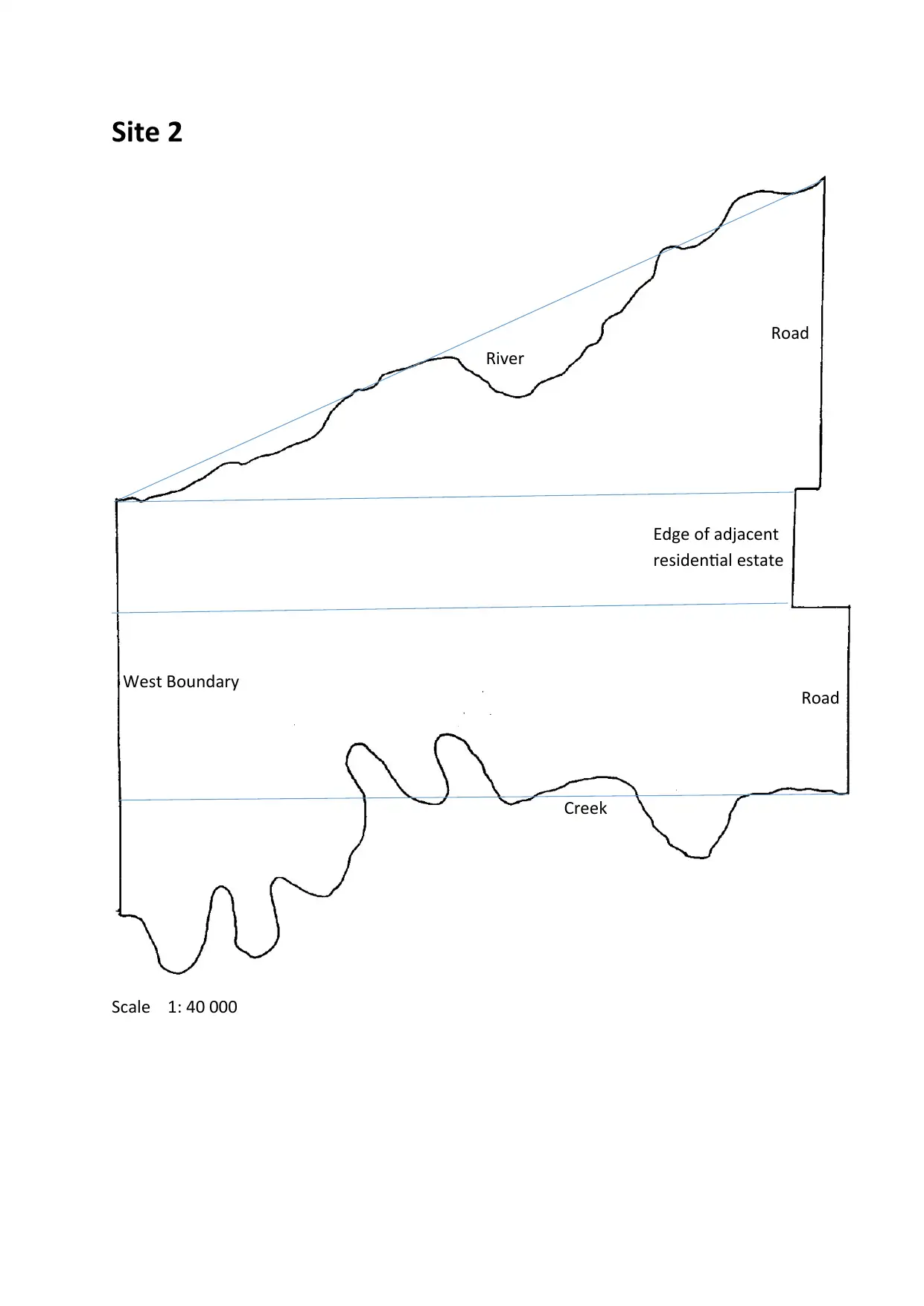
Site 2
Scale 1: 40 000
Creek
River
West Boundary
Edge of adjacent
residential estate
Road
Road
Scale 1: 40 000
Creek
River
West Boundary
Edge of adjacent
residential estate
Road
Road
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
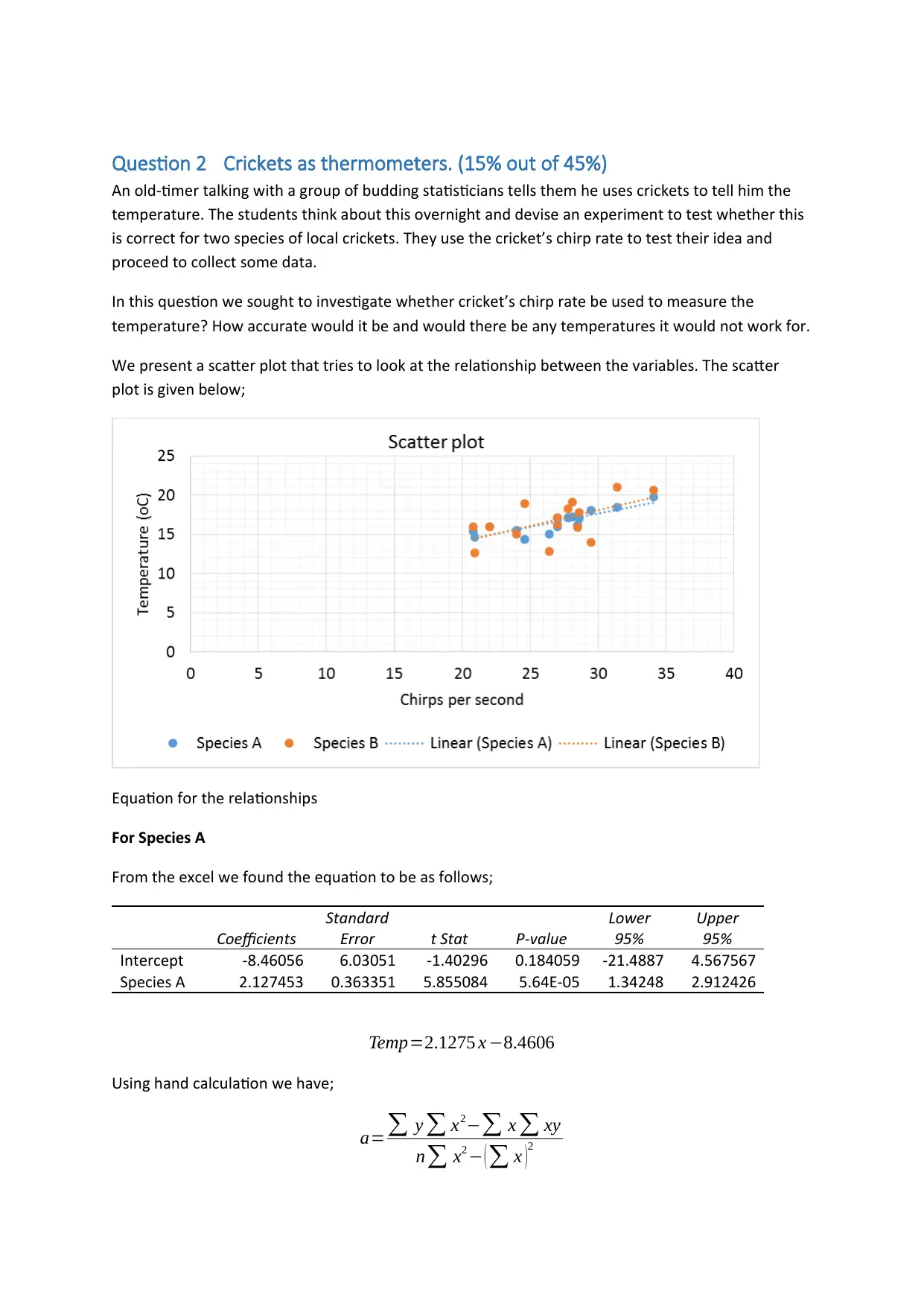
Question 2 Crickets as thermometers. (15% out of 45%)
An old-timer talking with a group of budding statisticians tells them he uses crickets to tell him the
temperature. The students think about this overnight and devise an experiment to test whether this
is correct for two species of local crickets. They use the cricket’s chirp rate to test their idea and
proceed to collect some data.
In this question we sought to investigate whether cricket’s chirp rate be used to measure the
temperature? How accurate would it be and would there be any temperatures it would not work for.
We present a scatter plot that tries to look at the relationship between the variables. The scatter
plot is given below;
Equation for the relationships
For Species A
From the excel we found the equation to be as follows;
Coefficients
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Intercept -8.46056 6.03051 -1.40296 0.184059 -21.4887 4.567567
Species A 2.127453 0.363351 5.855084 5.64E-05 1.34248 2.912426
Temp=2.1275 x −8.4606
Using hand calculation we have;
a=∑ y ∑ x2−∑ x ∑ xy
n∑ x2 − ( ∑ x )
2
An old-timer talking with a group of budding statisticians tells them he uses crickets to tell him the
temperature. The students think about this overnight and devise an experiment to test whether this
is correct for two species of local crickets. They use the cricket’s chirp rate to test their idea and
proceed to collect some data.
In this question we sought to investigate whether cricket’s chirp rate be used to measure the
temperature? How accurate would it be and would there be any temperatures it would not work for.
We present a scatter plot that tries to look at the relationship between the variables. The scatter
plot is given below;
Equation for the relationships
For Species A
From the excel we found the equation to be as follows;
Coefficients
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Intercept -8.46056 6.03051 -1.40296 0.184059 -21.4887 4.567567
Species A 2.127453 0.363351 5.855084 5.64E-05 1.34248 2.912426
Temp=2.1275 x −8.4606
Using hand calculation we have;
a=∑ y ∑ x2−∑ x ∑ xy
n∑ x2 − ( ∑ x )
2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

b= n∑ xy−∑ x ∑ y
n∑ x2− ( ∑ x )
2
∑ y=400.7, ∑ x =248, ∑ y2 =10901.25, ∑ x2=4131.86, ∑ xy =6692.12
a=∑ y ∑ x2−∑ x ∑ xy
n∑ x2 − (∑ x )2 = 400.7∗4131.86−248∗6692.12
15∗4131.86−2482 =−8.4606
b= n∑ xy−∑ x ∑ y
n∑ x2− (∑ x )2 = 15∗6692.12−248∗400.7
15∗4131.86−2482 =2.1275
Estimation of the chirp rate at 45 degrees Celsius;
Temp=2.1275 x −8.4606
45=2.1275 x−8.4606
2.1275 x=45+ 8.4606=53.4606
x= 53.4606
2.1275 =25.13
Hence the chirp rate is 25.13/second at 45 degrees
For Species B
From the excel we found the equation to be as follows;
Coefficients
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Intercept 12.18787 5.546636 2.197345 0.046725 0.205095 24.17065
Species B 0.865985 0.327131 2.647212 0.020118 0.159262 1.572709
Temp=0.866 x+12.1879
Using hand calculation we have;
a=∑ y ∑ x2−∑ x ∑ xy
n∑ x2 − ( ∑ x )
2
b= n∑ xy−∑ x ∑ y
n∑ x2− ( ∑ x )
2
∑ y=400.7, ∑ x =251.6, ∑ y2 =10901.25, ∑ x2=4312.28, ∑ xy =6800.84
n∑ x2− ( ∑ x )
2
∑ y=400.7, ∑ x =248, ∑ y2 =10901.25, ∑ x2=4131.86, ∑ xy =6692.12
a=∑ y ∑ x2−∑ x ∑ xy
n∑ x2 − (∑ x )2 = 400.7∗4131.86−248∗6692.12
15∗4131.86−2482 =−8.4606
b= n∑ xy−∑ x ∑ y
n∑ x2− (∑ x )2 = 15∗6692.12−248∗400.7
15∗4131.86−2482 =2.1275
Estimation of the chirp rate at 45 degrees Celsius;
Temp=2.1275 x −8.4606
45=2.1275 x−8.4606
2.1275 x=45+ 8.4606=53.4606
x= 53.4606
2.1275 =25.13
Hence the chirp rate is 25.13/second at 45 degrees
For Species B
From the excel we found the equation to be as follows;
Coefficients
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Intercept 12.18787 5.546636 2.197345 0.046725 0.205095 24.17065
Species B 0.865985 0.327131 2.647212 0.020118 0.159262 1.572709
Temp=0.866 x+12.1879
Using hand calculation we have;
a=∑ y ∑ x2−∑ x ∑ xy
n∑ x2 − ( ∑ x )
2
b= n∑ xy−∑ x ∑ y
n∑ x2− ( ∑ x )
2
∑ y=400.7, ∑ x =251.6, ∑ y2 =10901.25, ∑ x2=4312.28, ∑ xy =6800.84

a=∑ y ∑ x2−∑ x ∑ xy
n∑ x2 − (∑ x )2 = 400.7∗4312.28−251.6∗6800.84
15∗4312.28−251.62 =12.1879
b= n∑ xy−∑ x ∑ y
n∑ x2− ( ∑ x )
2 = 15∗6800.84−251.6∗400.7
15∗4312.28−251.62 =0.866
Estimation of the temperature when the chirp rate is zero;
Temp=0.866 x+12.1879
Temp=0.866(0)+12.1879
Temp=12.1879
Hence the temperature would be 12.1879 degrees when the species would stop chirping.
Comparing the two relationships.
From the regression analysis, the R-Squared value for the species A is 0.7250; implying that 72.5% of
the variation in the temperature is explained by species A.
On the other hand, the R-Squared value for the species B is 0.3503; implying that only 35.03% of the
variation in the temperature is explained by species B.
The above findings clearly shows that the model involving species A is more effective in terms of
determining the temperature as compared to the one involving species B.
Table 2.1: Chirp rate of crickets at different temperatures.
Chirps per second
Temperature (oC) Species A Species B
20.8 15.4 16.0
20.9 14.7 12.7
22 16.0 16.0
24 15.5 15.0
24.6 14.4 18.9
26.4 15.0 12.8
27 17.1 17.1
27 16.0 16.3
27.8 17.1 18.3
28.1 17.2 19.1
28.5 16.2 15.9
28.6 17.0 17.8
29.5 18.1 14.0
31.4 18.5 21.0
34.1 19.8 20.7
n∑ x2 − (∑ x )2 = 400.7∗4312.28−251.6∗6800.84
15∗4312.28−251.62 =12.1879
b= n∑ xy−∑ x ∑ y
n∑ x2− ( ∑ x )
2 = 15∗6800.84−251.6∗400.7
15∗4312.28−251.62 =0.866
Estimation of the temperature when the chirp rate is zero;
Temp=0.866 x+12.1879
Temp=0.866(0)+12.1879
Temp=12.1879
Hence the temperature would be 12.1879 degrees when the species would stop chirping.
Comparing the two relationships.
From the regression analysis, the R-Squared value for the species A is 0.7250; implying that 72.5% of
the variation in the temperature is explained by species A.
On the other hand, the R-Squared value for the species B is 0.3503; implying that only 35.03% of the
variation in the temperature is explained by species B.
The above findings clearly shows that the model involving species A is more effective in terms of
determining the temperature as compared to the one involving species B.
Table 2.1: Chirp rate of crickets at different temperatures.
Chirps per second
Temperature (oC) Species A Species B
20.8 15.4 16.0
20.9 14.7 12.7
22 16.0 16.0
24 15.5 15.0
24.6 14.4 18.9
26.4 15.0 12.8
27 17.1 17.1
27 16.0 16.3
27.8 17.1 18.3
28.1 17.2 19.1
28.5 16.2 15.9
28.6 17.0 17.8
29.5 18.1 14.0
31.4 18.5 21.0
34.1 19.8 20.7
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Question 3 Australia vs Great Britain at the Olympics 15% out of 45%
Australia and Great Britain have actively competed against each other at the Olympics games since
World War II. Some people would think that Great Britain with its larger population would outscore
Australia, yet both nations have collected a similar overall total of medals – Australia 471 medals
compared with Great Britain 494 medals since 1948.
But when comparing both nations’ medal tallies over time, which nation has been most consistent in
terms of overall performance?
So this task sought to make a comparison of the total medal tallies for Australia and Great Britain at
every Olympic Games since World War II as well as to determine which nation has had the most
consistent performance.
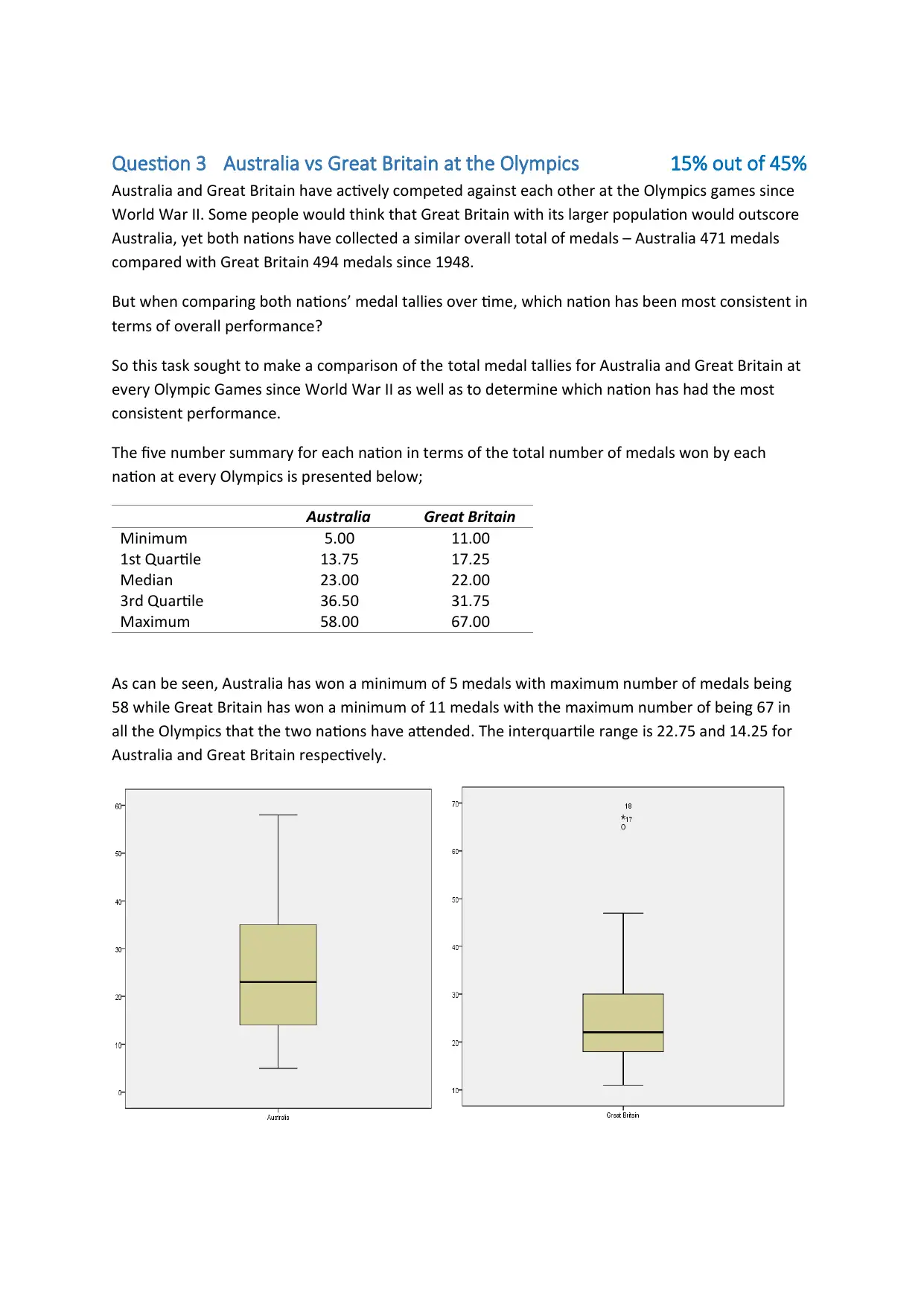
The five number summary for each nation in terms of the total number of medals won by each
nation at every Olympics is presented below;
Australia Great Britain
Minimum 5.00 11.00
1st Quartile 13.75 17.25
Median 23.00 22.00
3rd Quartile 36.50 31.75
Maximum 58.00 67.00
As can be seen, Australia has won a minimum of 5 medals with maximum number of medals being
58 while Great Britain has won a minimum of 11 medals with the maximum number of being 67 in
all the Olympics that the two nations have attended. The interquartile range is 22.75 and 14.25 for
Australia and Great Britain respectively.
Australia and Great Britain have actively competed against each other at the Olympics games since
World War II. Some people would think that Great Britain with its larger population would outscore
Australia, yet both nations have collected a similar overall total of medals – Australia 471 medals
compared with Great Britain 494 medals since 1948.
But when comparing both nations’ medal tallies over time, which nation has been most consistent in
terms of overall performance?
So this task sought to make a comparison of the total medal tallies for Australia and Great Britain at
every Olympic Games since World War II as well as to determine which nation has had the most
consistent performance.
The five number summary for each nation in terms of the total number of medals won by each
nation at every Olympics is presented below;
Australia Great Britain
Minimum 5.00 11.00
1st Quartile 13.75 17.25
Median 23.00 22.00
3rd Quartile 36.50 31.75
Maximum 58.00 67.00
As can be seen, Australia has won a minimum of 5 medals with maximum number of medals being
58 while Great Britain has won a minimum of 11 medals with the maximum number of being 67 in
all the Olympics that the two nations have attended. The interquartile range is 22.75 and 14.25 for
Australia and Great Britain respectively.

Boxplot were further plotted to check on the distribution of the medals for the two nations, as can
be seen, there seems to be outliers for the Great Britain but no outliers for Australia. This shows that
Australia has been the most consistent nation in terms of overall performance.
Comparing performance of the two nations
A comparison of the performance of the two nations was done where we sought to check whether
there is a significant difference in terms of the performance of the two nations for all the past
Olympics. The hypothesis tested is as follows;
H0 : μ1=μ2
H A : μ1 ≠ μ2
To test this, we used two-sample t-test and tested it at 5% level of significance. Results are given
below;
t-Test: Two-Sample Assuming Equal
Variances
Austr
alia
Great
Britai
n
Mean
26.16
667
27.44
444
Variance
230.0
294
274.8
497
Observations 18 18
Pooled Variance
252.4
395
Hypothesized Mean
Difference 0
df 34
t Stat
-
0.241
27
P(T<=t) one-tail
0.405
399
t Critical one-tail
1.690
924
P(T<=t) two-tail
0.810
797
t Critical two-tail
2.032
245
As can be seen, the p-value is given as 0.811 (a value greater than 5% level of significance), we thus
fail to reject the null hypothesis and conclude that there is no significant difference in terms of the
performance for the two nations.
be seen, there seems to be outliers for the Great Britain but no outliers for Australia. This shows that
Australia has been the most consistent nation in terms of overall performance.
Comparing performance of the two nations
A comparison of the performance of the two nations was done where we sought to check whether
there is a significant difference in terms of the performance of the two nations for all the past
Olympics. The hypothesis tested is as follows;
H0 : μ1=μ2
H A : μ1 ≠ μ2
To test this, we used two-sample t-test and tested it at 5% level of significance. Results are given
below;
t-Test: Two-Sample Assuming Equal
Variances
Austr
alia
Great
Britai
n
Mean
26.16
667
27.44
444
Variance
230.0
294
274.8
497
Observations 18 18
Pooled Variance
252.4
395
Hypothesized Mean
Difference 0
df 34
t Stat
-
0.241
27
P(T<=t) one-tail
0.405
399
t Critical one-tail
1.690
924
P(T<=t) two-tail
0.810
797
t Critical two-tail
2.032
245
As can be seen, the p-value is given as 0.811 (a value greater than 5% level of significance), we thus
fail to reject the null hypothesis and conclude that there is no significant difference in terms of the
performance for the two nations.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
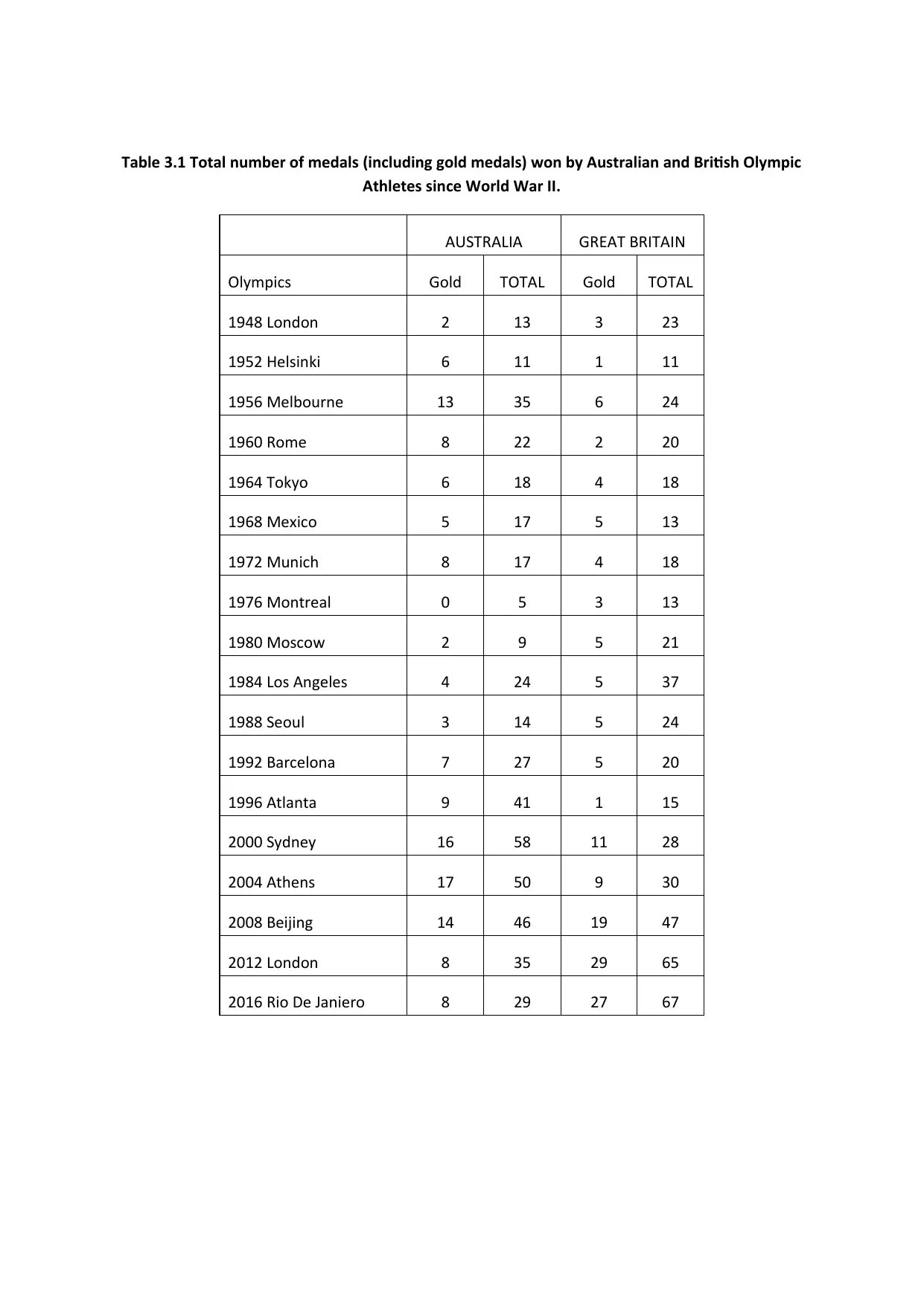
Table 3.1 Total number of medals (including gold medals) won by Australian and British Olympic
Athletes since World War II.
AUSTRALIA GREAT BRITAIN
Olympics Gold TOTAL Gold TOTAL
1948 London 2 13 3 23
1952 Helsinki 6 11 1 11
1956 Melbourne 13 35 6 24
1960 Rome 8 22 2 20
1964 Tokyo 6 18 4 18
1968 Mexico 5 17 5 13
1972 Munich 8 17 4 18
1976 Montreal 0 5 3 13
1980 Moscow 2 9 5 21
1984 Los Angeles 4 24 5 37
1988 Seoul 3 14 5 24
1992 Barcelona 7 27 5 20
1996 Atlanta 9 41 1 15
2000 Sydney 16 58 11 28
2004 Athens 17 50 9 30
2008 Beijing 14 46 19 47
2012 London 8 35 29 65
2016 Rio De Janiero 8 29 27 67
Athletes since World War II.
AUSTRALIA GREAT BRITAIN
Olympics Gold TOTAL Gold TOTAL
1948 London 2 13 3 23
1952 Helsinki 6 11 1 11
1956 Melbourne 13 35 6 24
1960 Rome 8 22 2 20
1964 Tokyo 6 18 4 18
1968 Mexico 5 17 5 13
1972 Munich 8 17 4 18
1976 Montreal 0 5 3 13
1980 Moscow 2 9 5 21
1984 Los Angeles 4 24 5 37
1988 Seoul 3 14 5 24
1992 Barcelona 7 27 5 20
1996 Atlanta 9 41 1 15
2000 Sydney 16 58 11 28
2004 Athens 17 50 9 30
2008 Beijing 14 46 19 47
2012 London 8 35 29 65
2016 Rio De Janiero 8 29 27 67
1 out of 10
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.
