Experimental Design and Data Analysis

This document provides solutions to problems related to experimental design and data analysis. It includes graphs, calculations of mean and median, probability calculations, confidence intervals, hypothesis testing, and descriptive statistics. The subject is Experimental Design and Data Analysis.

EXPERIMENTAL DESIGN AND DATA ANALYSIS
STUDENT ID:
[Pick the date]

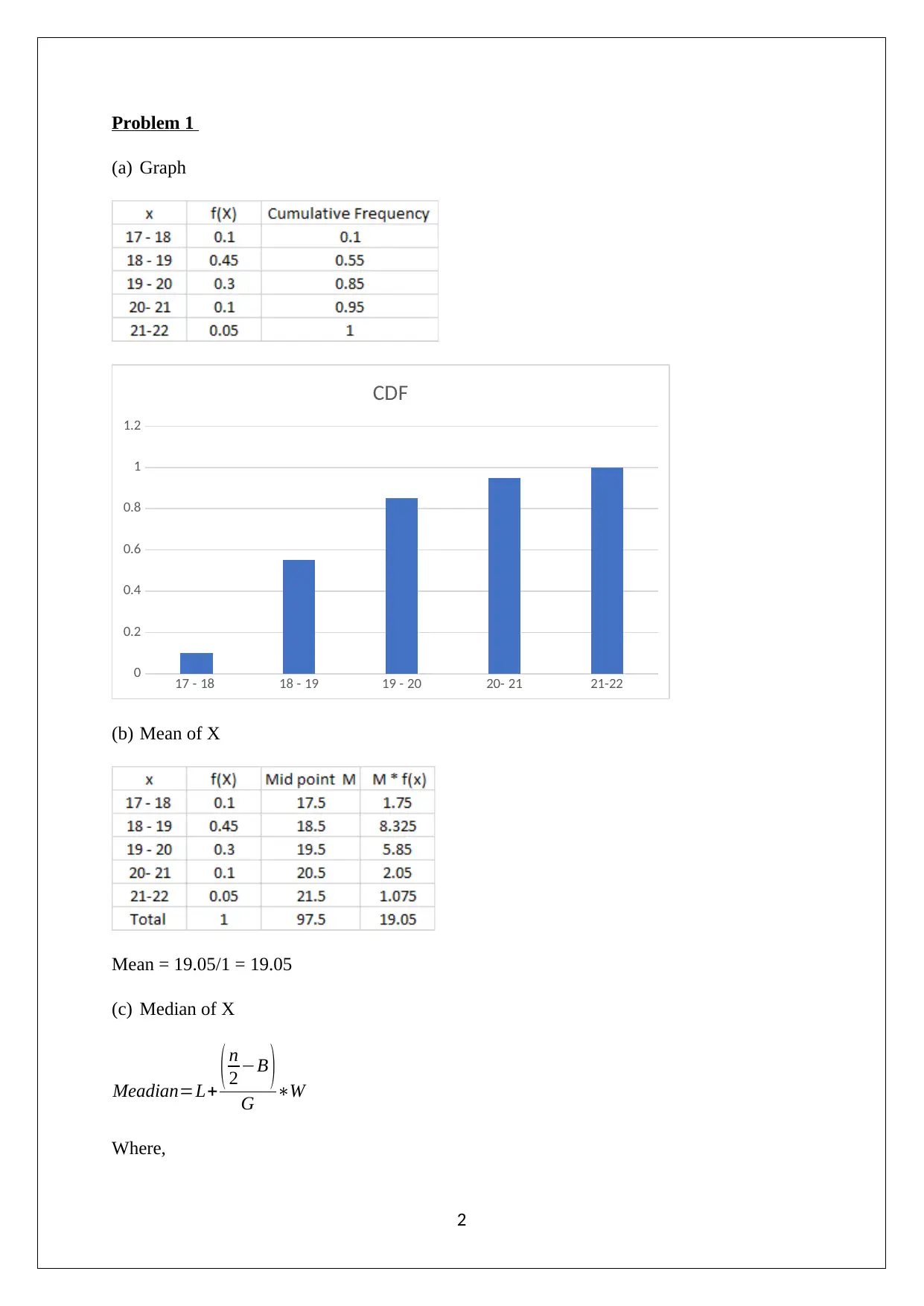
Problem 1
(a) Graph
17 - 18 18 - 19 19 - 20 20- 21 21-22
0
0.2
0.4
0.6
0.8
1
1.2
CDF
(b) Mean of X
Mean = 19.05/1 = 19.05
(c) Median of X
Meadian=L+ ( n
2 −B )
G ∗W
Where,
2

Median would lie in the interval of 18-19.
L=lower class boundary of median group=18 ,
n=Total frequency=1
B=cumulative frequency of groupbefore median group=0.1 ,
G=Frequency of median group=0.45 ,
W =group width=1
Meadian=18+ ( 1
2 −0.1 )
0.45 ∗1=18.89
(d) Probability that age is more than 18 = 0.45+0.3+0.1+0.05 = 0.9
Probability of success = 0.9
Number of students = 5
Probability that at least four of them are over 18 (P)= P(4) + P(5)
Now,
Similarly,
3

Probability that at least four of them are over 18 (P)= P(4) + P(5) = 0.32805 + 0.59049 =
0.91854
Hence, there is 0.91854 probability that at least four of them are over 18 years.
(e) Probability that average age is less than 19 years.
Mean = 19.05
Standard deviation = 1.0153
Sample size= 250
Standard error = 1.0153 / sqrt (250) = 0.0642
4

Hence, there is 0.2177 probability that average age is less than 19 years.
(f) Null and alternative hypothesis
Null hypothesis H0: The proportion of first year EDDA students who are under 20 years does
not significantly differ from corresponding proportion for the general first year cohort.
Alternative hypothesis Ha: The proportion of first year EDDA students who are under 20
years does significantly differ from corresponding proportion for the general first year cohort.
Problem 2
(a) True mean of protein in a package
Number of observations = 15
Sum of observation = 2396.60
Mean = Sum of observation/ Number of observations
Mean = 2396.60/15 = 159.77
(b) 95% confidence interval of true mean
5

Standard deviation = 3.462
Mean = 159.77
Degree of freedom = n-1 = 15-1 = 14
The t value for 95% confidence interval = 2.1447
Standard error = Standard deviation / sqrt (15) = 0.8940
Margin of error = t value * Standard error = 2.1447* 0.8940 = 1.9173
Now,
Lower limit of 95% confidence interval = Mean – Margin of error = 159.77-1.9173 = 157.86
Upper limit of 95% confidence interval = Mean + Margin of error = 159.77+1.9173 = 161.69
95% Confidence interval = [ 158.86 161.69]
It can be said with 95% confidence that the true mean of protein in a packet would fall within
158.86 grams and 161.69 grams.
(c) 95% confidence interval of true mean
Standard deviation = 3.462
Mean = 159.77
Degree of freedom = n-1 = 15-1 = 14
The t value for 98% confidence interval = 2.624
Standard error = Standard deviation / sqrt (15) = 0.8940
Margin of error = t value * Standard error = 2.624* 0.8940 = 2.3462
Now,
Lower limit of 98% confidence interval = Mean – Margin of error = 159.77-2.3462 = 157.43
Upper limit of 98% confidence interval = Mean + Margin of error = 159.77+2.3462= 162.12
98% Confidence interval = [157.43 162.12]
6

It can be said with 98% confidence that the true mean of protein in a packet would fall within
157.43 grams and 162.12 grams.
(d) The z value corresponding to 95% probability = 1.645
Let the amount is x grams
z= x−159.77
0.894
1.645= x−159.77
0.894
x=161.24
Hence, the amount of protein in packet would be greater than 161.24 grams. Thus, the
suitable interval would be 161.24 g to 165 g.
(e) Since the amount of protein computed in part c does lie in the 95% confidence interval
estimated in part b. hence the claim made by advertisement would be considered as true.
(f) The descriptive statistics for the sample data is illustrated below.
It is evident from the above descriptive statistics that there is a significant amount of positive
skew that is present. For a normal distribution, the amount of skew ought to be zero or else
7

the shape of the distribution would not be symmetric. Hence, the given distribution cannot be
considered as normally distributed.
(g) Sample size =?
Margin of error = 1
Z value for 95% confidence interval = 1.960
Standard deviation = 3.4623
Let the sample size be N
Now,
N= ( Z )2∗( Standard deviation )2
( Margin of error )2
N= 1.962∗3.46232
1 =46.05 47
Thus, the minimum sample size would be 47.
8