Exponential and Logarithmic Function

This document provides solutions and graphs for exponential and logarithmic functions. It covers topics such as domain, range, series, scatter plots, linear regression, population growth, and compound interest.

Running head: EXPONENTIAL AND LOGARITHMIC FUNCTION
Exponential and Logarithmic Function
Name of the Student:
Name of the University:
Author Note:

1EXPONENTIAL AND LOGARITHMIC FUNCTION
Table of Contents
Solution 1...................................................................................................................................3
Solution 2...................................................................................................................................3
Solution 3...................................................................................................................................4
Solution 4...................................................................................................................................4
Solution 5...................................................................................................................................4
Solution 6...................................................................................................................................5
Solution 7...................................................................................................................................5
Solution 8...................................................................................................................................5
Solution 9...................................................................................................................................5
Solution 10. A............................................................................................................................5
Solution 10. B.............................................................................................................................6
Solution 11. A............................................................................................................................6
Solution 11. B.............................................................................................................................7
Solution 12.................................................................................................................................7
Solution 13.................................................................................................................................7
Solution 14.................................................................................................................................7
Solution 15.................................................................................................................................8
Solution 16. A............................................................................................................................8
Solution 16. B.............................................................................................................................9
Solution 16. C.............................................................................................................................9
Solution 17.................................................................................................................................9

2EXPONENTIAL AND LOGARITHMIC FUNCTION
Solution 18...............................................................................................................................10
Solution 19...............................................................................................................................10
Solution 20...............................................................................................................................11
Solution21................................................................................................................................11
Solution 22...............................................................................................................................11
Solution 23...............................................................................................................................12
Solution 24...............................................................................................................................12
Solution 25...............................................................................................................................12
Solution 26...............................................................................................................................13
Solution 27. A..........................................................................................................................13
Solution 27. B...........................................................................................................................14
Solution 27. C...........................................................................................................................14

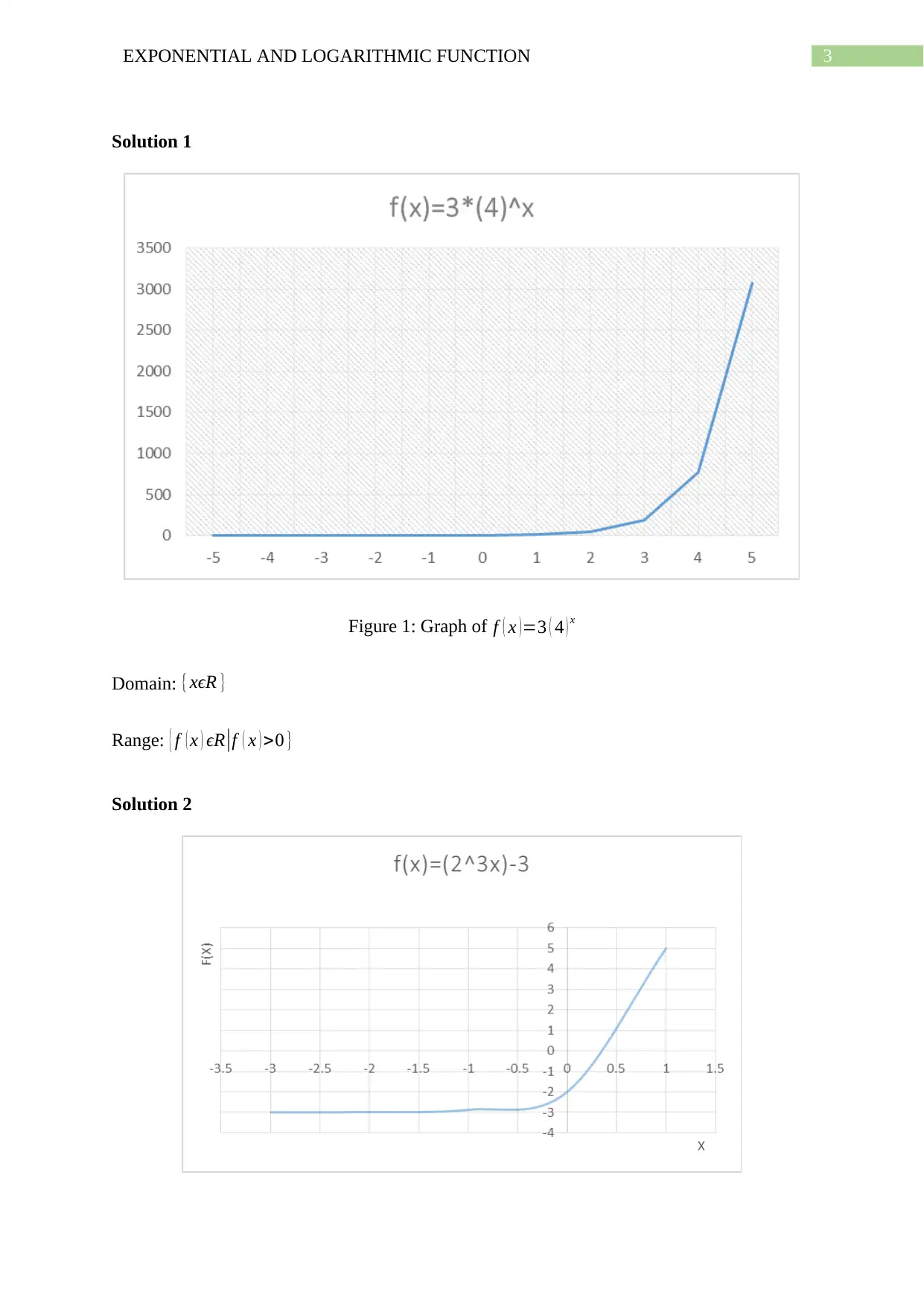
3EXPONENTIAL AND LOGARITHMIC FUNCTION
Solution 1
Figure 1: Graph of f ( x ) =3 ( 4 ) x
Domain: {xϵR }
Range: { f ( x ) ϵR|f ( x ) >0 }
Solution 2

4EXPONENTIAL AND LOGARITHMIC FUNCTION
Figure 2: Graph of f ( x )=23 x−3
Domain: {xϵR }
Range: { f ( x ) ϵR|f ( x ) >−3 }
Solution 3
2x−1=8x +3
2x−1=23(x+3 )
x−1=3 ( x +3 )
3 x−x=−1−3
x=−4
2 =−2
Solution 4
52 x+1 2=2510 x−12
52 x+12=52(10 x−12)
2 x+12=2(10 x−12)
20 x−2 x=12+24
18 x=36
x= 36
18 =2
Solution 5
0.75, 3, 12, . . .,
The nth term of the series is tn=4 n

5EXPONENTIAL AND LOGARITHMIC FUNCTION
Solution 6
0.4, -2, 10, …
The nth term of the series istn=−5 n.
Solution 7
log 8 64 ¿ log8 82
¿ 2 log8 8=2
Solution 8
log7 1 ¿ log7 70
¿ 0 log7 7=0
Solution 9
log5
1
25 ¿ log5 5−2
¿−2 log5 5=−2
Solution 10. A
n(t)=920 log10(t−1)
n ( 4 ) =920 log10 ( 4−1 )
n( 4)=920 log10 3
n ( 4 )=920∗0.477
n( 4)=438.95
n(4) ≅ 439

6EXPONENTIAL AND LOGARITHMIC FUNCTION
After 4 months, there will be 439 dolphins in the ocean region.
Solution 10. B
n(t)=920 log10(t−1)
n ( 24 ) =920 log10 ( 24−1 )
n ( 24 )=920 log10 23
n ( 24 ) =920∗1.362
n ( 24 )=1252.79
n(24)≅ 1253
After 2 years that means 24 months, there will be 1253 dolphins in the ocean region.
Solution 11. A
Distance in Miles Fare in Dollars
2 9.25
5 19.75
8 29.75
12 44.5
The scatter plot of the above data presents an upward rising linear relationship
between distance and fare. So, the linear regression model will work best with the data.

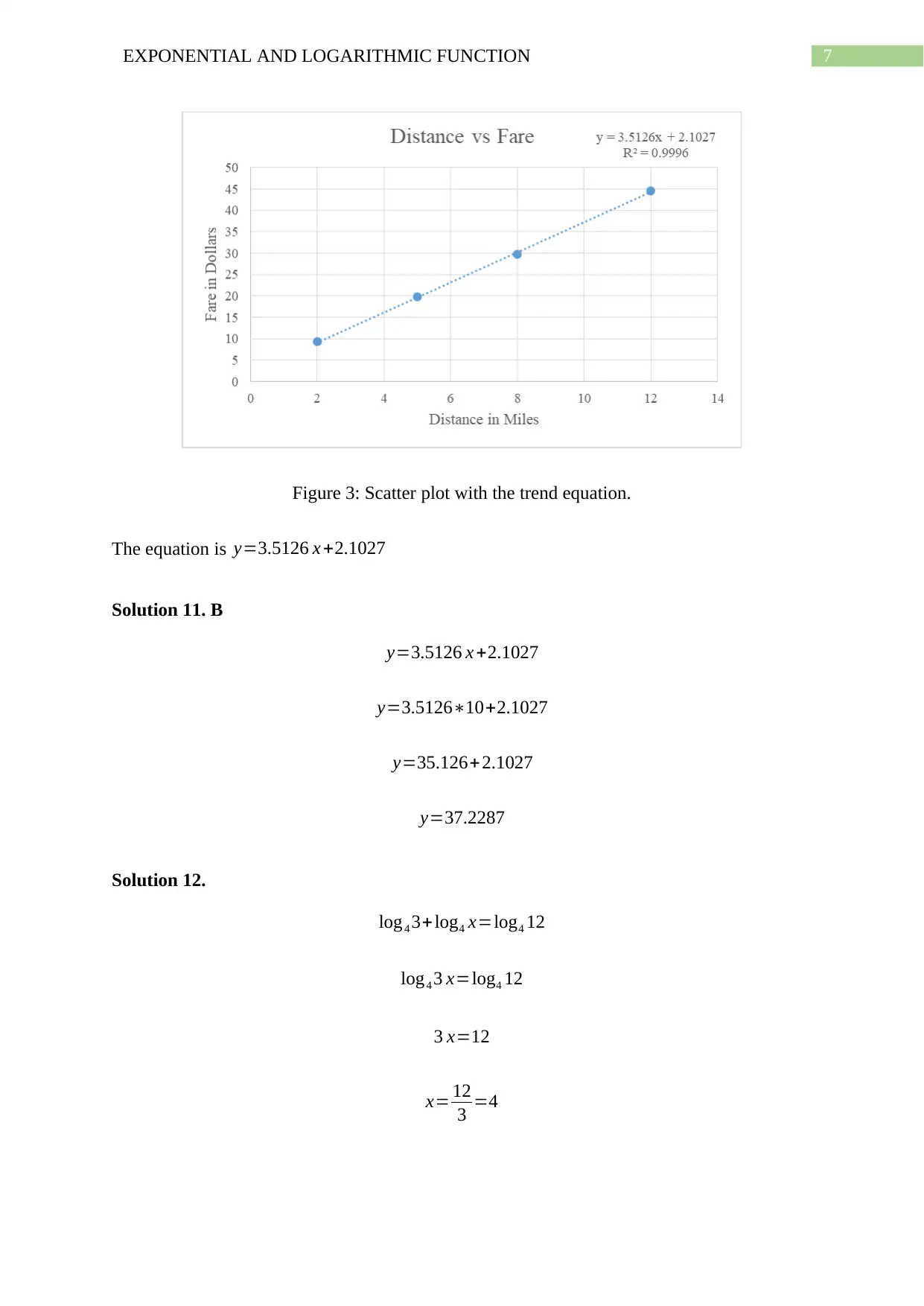
7EXPONENTIAL AND LOGARITHMIC FUNCTION
Figure 3: Scatter plot with the trend equation.
The equation is y=3.5126 x +2.1027
Solution 11. B
y=3.5126 x +2.1027
y=3.5126∗10+2.1027
y=35.126+2.1027
y=37.2287
Solution 12.
log4 3+log4 x=log4 12
log4 3 x=log4 12
3 x=12
x= 12
3 =4

8EXPONENTIAL AND LOGARITHMIC FUNCTION
Solution 13
log7 6−log7 2=log7 x
log7
6
2 =log7 x
log7 3=log7 x
x=3
Solution 14
4 log2 x =log2 81
4 log2 x =log2 34
4 log2 x =4 log2 3
x=3
Solution 15
log6 x +log6 (x +5)=2
log6 x ( x +5 ) =2 log6 6
log6 x ( x +5 ) =log6 36
x ( x+ 5)=3 6
x2+ 5 x−36=0
x2+9 x−4 x−36=0
x ( x +9 ) −4 (x +9)=0
(x +9)(x−4)=0

9EXPONENTIAL AND LOGARITHMIC FUNCTION
x=−9,4
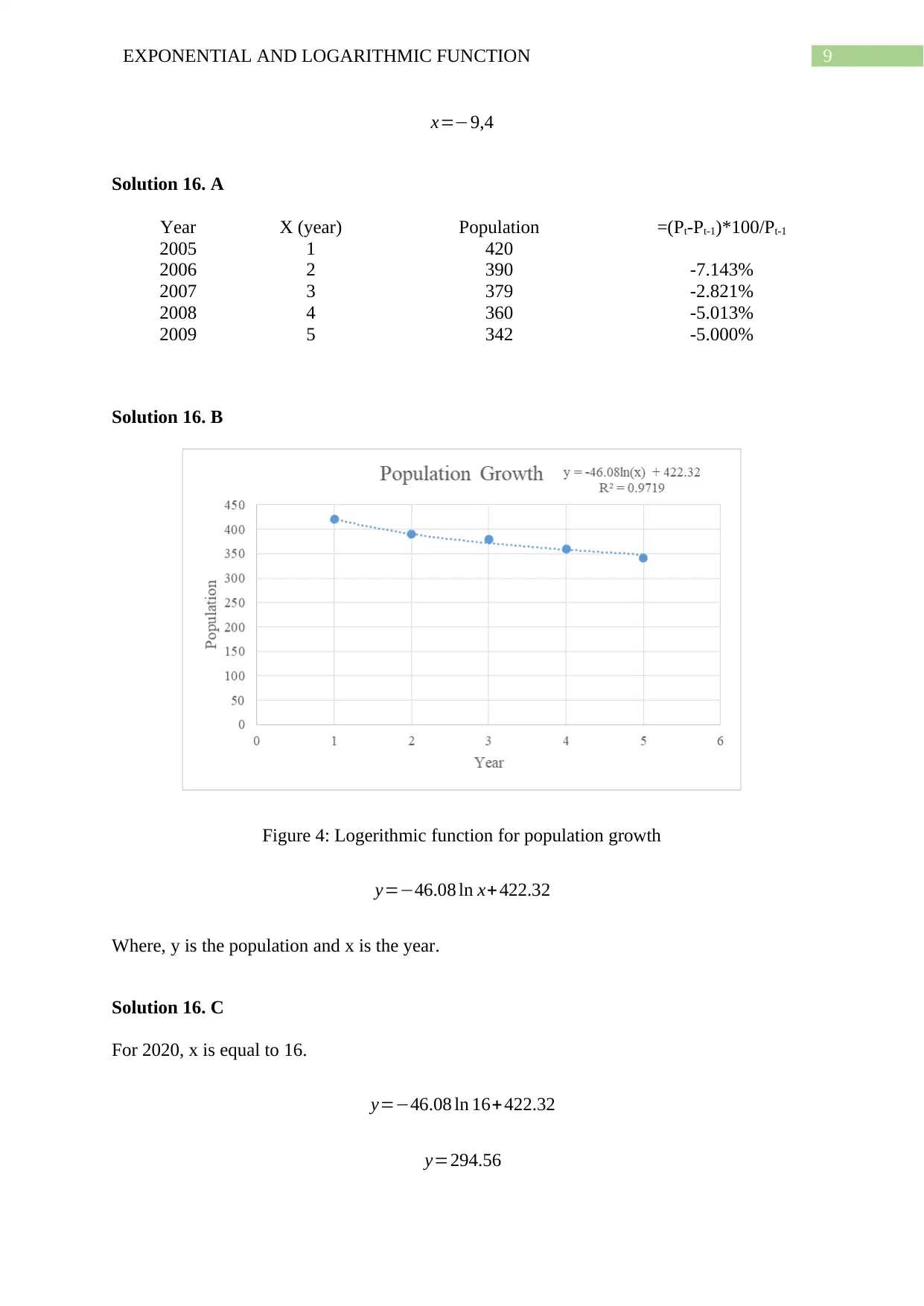
Solution 16. A
Year X (year) Population =(Pt-Pt-1)*100/Pt-1
2005 1 420
2006 2 390 -7.143%
2007 3 379 -2.821%
2008 4 360 -5.013%
2009 5 342 -5.000%
Solution 16. B
Figure 4: Logerithmic function for population growth
y=−46.08 ln x+422.32
Where, y is the population and x is the year.
Solution 16. C
For 2020, x is equal to 16.
y=−46.08 ln 16+422.32
y=294.56

10EXPONENTIAL AND LOGARITHMIC FUNCTION
y ≅ 295
Solution 17
5x=60
ln 5x=ln 60
x ln5=ln60=ln 5+ln 12
x=1+ ln 12
ln 5
x=1+1.544=2.544
Solution 18
4 x2
=21
ln 4x2
=ln 21
x2 ln 4=ln 21
x2= ln 21
ln 4 =2.1962
x=± 1.4819
Solution 19
3x−2=4x
ln 3x−2=ln 4 x
( x−2 ) ln 3=x ln 4
x−2
x = ln 4
ln 3

11EXPONENTIAL AND LOGARITHMIC FUNCTION
x−2+ x
x−2−x = ln 4 +ln 3
ln 4−ln3
2 x−2
−2 = ln 12
ln 4
3
1−x=8.6377
x=−7.6377
Solution 20
4 ex−6=11
ln 4 ex=ln 17
ln 4+ x ln e=ln 17
ln 4+ x=ln17
x=ln17−ln 4
x=1.4469
Solution21
3 e− x+ 4=17
ln 3 e− x=ln 13
ln 3−x lne=ln13
ln 3−x=ln 13
x=ln3−ln 13
x=−1.4663

12EXPONENTIAL AND LOGARITHMIC FUNCTION
Solution 22
2 e3 x−8=21
ln 2 e3 x=ln29
ln 2+3 x ln e=ln 29
ln 2+3 x=ln29
x= 1
3 (ln 29−ln 2)
x=0.8914
Solution 23
log25 x= 3
2
x= ( 25 )
3
2
x=125
Solution 24
log9 81=x
log9 92=x
2 log9 9=x
x=2
Solution 25
log6 ( 5 x−3 ) =log6 ( x+ 9 )
log6 ( 5 x−3 ) −log6 ( x+ 9 )=0

13EXPONENTIAL AND LOGARITHMIC FUNCTION
log6
( 5 x −3 )
x+ 9 =0
( 5 x−3 )
( x+ 9 ) =60 =1
( 5 x−3 ) =x+9
¿
4 x=12
x=3
Solution 26
log8 ( x2 +6 ) =log8 ( 5 x )
log8 ( x2 +6 ) −log8 ( 5 x ) =0
log8
( x2+6 )
5 x =0
( x2+6 )
5 x =80
x2+6=5 x
x2−5 x+ 6=0
(x−3)(x−2)=0
x=3,2
Solution 27. A
The formula for future amount when the interest is continuously compounded A=P ert .
Future amount, A= $2400

14EXPONENTIAL AND LOGARITHMIC FUNCTION
Present value, P= $2000
Interest, r= 2.5%
Time, t=?
A=P ert
2400=2000 e0.025 t
6
5 =e0.025 t
ln 6
5 =0.025 t ln e
t= 1
0.025 ln 6
5
t=7.293
Solution 27. B
Future amount, A=2P
A=P ert
2 P=P ert
2=e0.025 t
ln 2=0.025t ln e
t= 1
0.025 ln2
t=27.726

15EXPONENTIAL AND LOGARITHMIC FUNCTION
Solution 27. C
Future amount, A= $5000
Interest, r= 2.5%
Time, t=10 years
Present value, P=?
A=P ert
5000=P e0.025∗10
5000
P =e0.25
5000=1.284∗P
P= 5000
1.284 =3894.004