Your All-in-One AI-Powered Toolkit for Academic Success.

+13062052269

info@desklib.com

Available 24*7 on WhatsApp / Email

Company

Tools

Support

FIN201 – Corporate Finance: Investment Analysis and Capital Structure

Verified

Added on 2024/07/03

AI Summary

This document explores key concepts in corporate finance, including investment analysis and capital structure. It examines the payback period rule, net present value (NPV), and internal rate of return (IRR) as methods for evaluating investment proposals. The document also delves into the Modigliani-Miller (M&M) propositions, which provide insights into the relationship between capital structure and firm value. Through calculations and explanations, the document demonstrates how to apply these concepts in real-world scenarios.

Contribute Materials

Your contribution can guide someone’s learning journey. Share your documents today.

Unit: FIN201 – Corporate Finance
1

Secure Best Marks with AI Grader

Need help grading? Try our AI Grader for instant feedback on your assignments.

💎 Get Pro

Contents
Question 1:................................................................................................................................. 3
Question 2:................................................................................................................................. 6
Question 3:................................................................................................................................. 9
References:............................................................................................................................... 12
2

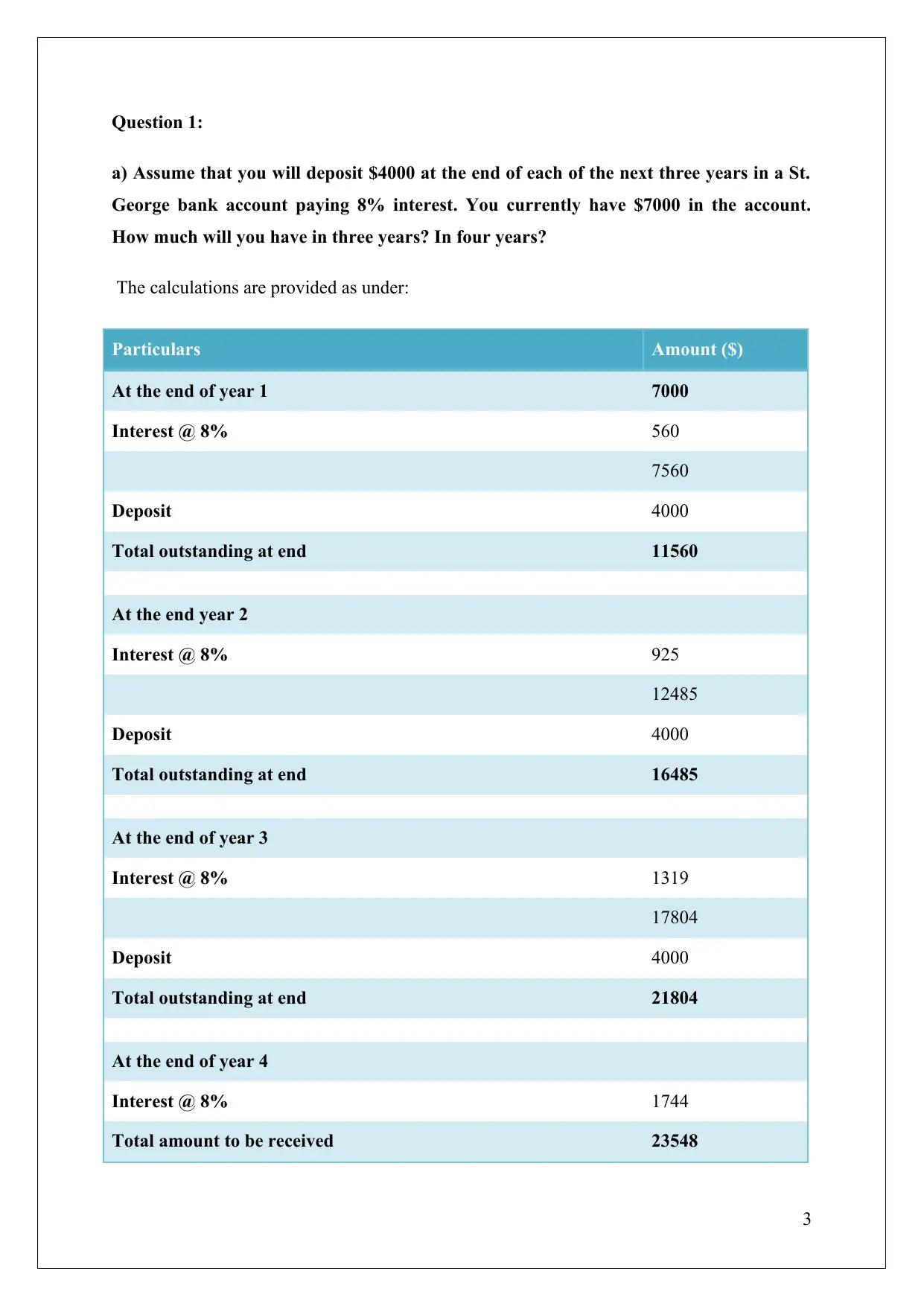
Question 1:
a) Assume that you will deposit $4000 at the end of each of the next three years in a St.
George bank account paying 8% interest. You currently have $7000 in the account.
How much will you have in three years? In four years?
The calculations are provided as under:
Particulars Amount ($)
At the end of year 1 7000
Interest @ 8% 560
7560
Deposit 4000
Total outstanding at end 11560
At the end year 2
Interest @ 8% 925
12485
Deposit 4000
Total outstanding at end 16485
At the end of year 3
Interest @ 8% 1319
17804
Deposit 4000
Total outstanding at end 21804
At the end of year 4
Interest @ 8% 1744
Total amount to be received 23548
3

b) You are looking into an investment that will pay you $12,000 per year for the next 10
years. If you require a 15% return, what is the most you would pay for this investment?
In order to calculate the investment required to be made in order to yearly payments of
$12000 with an interest of 15% following calculations will be performed.
Present Value = Future Value / (1+r)n
Particulars Amount
Payments 12000
Term 10
Interest Rate 15%
Amount to be invested -60,225.22₹
c) A bond has an 8% coupon, paid semi-annually. The face value is $100, and the bond
matures in 6 years. If the bond currently sells for $91.137, what is the yield to maturity?
What is the effective annual yield?
Yield to maturity = Yield to maturity can be referred to as the return in total which can be
expected by a bond which will be held till maturity. It can also be regarded as the internal rate
of return of an investment made in the bond (Damodaran, 2016).
The formula is presented as under:
YTM = (C + (F - P) / n) / ((F + P) / 2)
Where...
YTM = Yield to Maturity
C = Coupon or Interest Payment
F = Face Value
4

Paraphrase This Document

Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

💎 Try AI Paraphraser

P = Price
n = Years to Maturity
Now it can be established that,
YTM = [16 + (100 – 91137)/6] / (100 + 91137) / 2
YTM = 15175.5 / 45618.5
YTM = .3326
Or 33.26%
Effective annual yield = [1+ i/n]n – 1
= [1+.3326/6]6 – 1
= .4546 or 45.46%
5

Question 2:
a. Based on the payback period rule, which project would you pick? Explain.
Payback period for project A:
Payback period = 2 + 50/100
= 2.5 years
Payback period for project B:
Payback period = 1 + 150/200
= 1.75 years
Decision:
It can be established that the payback period in project B is 1.75 years which is less than
payback period of project A. It shows that the company will recover its cost incurred in the
relevant years calculated. And as the recoverable period is less in project B it will be
accepted.
b) Based on the NPV rule, which project would you pick? Explain.
Calculation of NPV for project A:
Particular Amount ($) P V F (15%)
Cost -250 1 -250
Cash inflow Y1 100 0.869 86.9
Cash inflow Y2 100 0.756 75.6
Cash inflow Y3 100 0.657 65.7
Cash inflow Y4 100 0.571 57.1
Present value of project 35.3
6

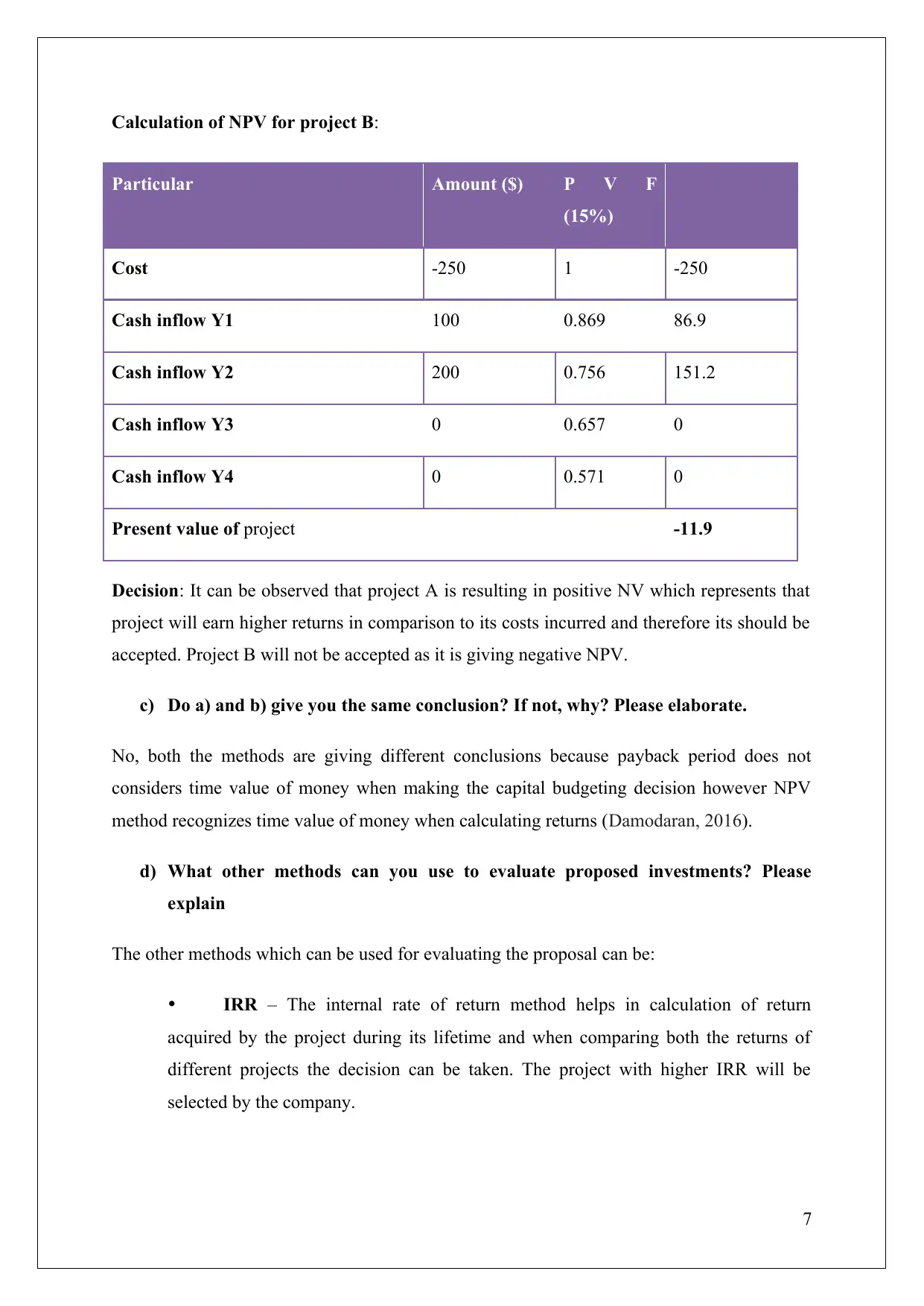
Calculation of NPV for project B:
Particular Amount ($) P V F
(15%)
Cost -250 1 -250
Cash inflow Y1 100 0.869 86.9
Cash inflow Y2 200 0.756 151.2
Cash inflow Y3 0 0.657 0
Cash inflow Y4 0 0.571 0
Present value of project -11.9
Decision: It can be observed that project A is resulting in positive NV which represents that
project will earn higher returns in comparison to its costs incurred and therefore its should be
accepted. Project B will not be accepted as it is giving negative NPV.
c) Do a) and b) give you the same conclusion? If not, why? Please elaborate.
No, both the methods are giving different conclusions because payback period does not
considers time value of money when making the capital budgeting decision however NPV
method recognizes time value of money when calculating returns (Damodaran, 2016).
d) What other methods can you use to evaluate proposed investments? Please
explain
The other methods which can be used for evaluating the proposal can be:
 IRR – The internal rate of return method helps in calculation of return
acquired by the project during its lifetime and when comparing both the returns of
different projects the decision can be taken. The project with higher IRR will be
selected by the company.
7

Secure Best Marks with AI Grader

Need help grading? Try our AI Grader for instant feedback on your assignments.

💎 Get Pro

 ARR – The average rate of return can be referred to another method of
making this decision as average returns can be calculated and the project with higher
return will be accepted.
8

Question 3:
1. The ABC Company has a WACC of 20%. Its cost of debt is 12%, which is equal to
the risk-free rate of interest. If ABC’s debt to equity ratio is 2, what is the cost of equity
capital? ABC’s equity beta is 1.5.
WACC = We*Ke + Wd*Kd
=.20 = .5*Ke + 1*.12
= .20 = .5Ke +.12
= Ke = .16
Therefore cost of equity is 16%
What are the M&M propositions I, II and III, please use graphs/charts and words to
explain.
The proposition I explains that the firm’s value does not depend on the structure of capital
(Vernimmen, et. al., 2014). The capital structure of the firm does not affect the value derived
from the operations. Let’s see the diagram presented below:
(Source: Fracassi, 2016)
It can be established that in left side of the diagram equity constitutes the major portion of
capital structure with 70% and the debt is only 30% however in right side diagram debt
constitutes 70% of the capital structure whereas equity is only 30%.
9

This is due to that reason that assets in both the capital structures are same. Therefore this
proposition says that the structuring of debt and equity in capital of the company is irrelevant
and the value of the firm is determined by its total assets.
The proposition II states that the value of the form is dependent on three factors consisting of
required rate of return, cost of debt and debt equity ratio of the firm.
(Source: Fracassi, 2016)
The above diagram shows that required rate of return is a straight line with a slope
(Vernimmen, et. al., 2014). There is an observation that when a company employs more debt
the risk of becoming bankrupt increases and increased debt employed in company requires
higher rate of returns to be expected.
Based on the M&M proposition II, what is the beta of the entire firm?
We know that,
WACC = Rf + B(Rm – Rf)
.20 = .12 + 1.5 (Rm - .12)
10

Paraphrase This Document

Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

💎 Try AI Paraphraser

.20 = .12 + 1.5Rm - .18
Rm = .17 or 17%
Now we can calculate firm beta,
.20 = .12 + B(.17 - .12)
.20 = .12 + B(.05)
B = 1.6
11

References:
 Damodaran, A., 2016. Damodaran on valuation: security analysis for investment and
corporate finance (Vol. 324). John Wiley & Sons.
 Ehrhardt, M.C. and Brigham, E.F., 2016. Corporate finance: A focused approach.
Cengage learning.
 Fracassi, C., 2016. Corporate finance policies and social networks. Management
Science, 63(8), pp.2420-2438.
 Vernimmen, P., Quiry, P., Dallocchio, M., Le Fur, Y. and Salvi, A., 2014. Corporate
finance: theory and practice. John Wiley & Sons.
 Vishny, R. and Zingales, L., 2017. Corporate Finance. Journal of Political
Economy, 125(6), pp.1805-1812.
12

1 out of 12

+13062052269

info@desklib.com

FIN201 – Corporate Finance: Investment Analysis and Capital Structure

Contribute Materials

Secure Best Marks with AI Grader

Paraphrase This Document

Secure Best Marks with AI Grader

Paraphrase This Document

Related Documents

Capital Structure Theories: Modigliani-Miller Propositions

Bond and Stock Valuation Assignment

Financial Modelling

Financial Management

Risk and Return Analysis for Cochlear Ltd

Finance