Finance and Capital Budgeting Assignment

This finance assignment comprises two main questions. The first focuses on the analysis of two bonds with differing interest rates and maturities, requiring calculation of their respective prices. The second question delves into capital budgeting by evaluating a proposed technology investment for Perth Projects Ltd. Students must analyze cash flows, calculate the net present value (NPV), and make a recommendation on whether to purchase the technology based on its financial viability.

KOI
Trimester 2, 2017
FIN700 – Financial Management
ASSIGNMENT– GROUP
Due date: Submit to your Tutor by the start of your Tutorial on
Monday, 11 September, 2017 or on Tuesday, 12 September, 2017.
Keep a soft copy in case of misadventure.
Penalties for late lodgment, as per the Subject Outline, will be strictly applied.
This Assignment consists of 4 problems, each involving
calculations, and in some cases recommendations.
You are required to complete this Assignment in Groups of 2 or 3 or 4 people.
Groups of 1 or more than 4 persons will incur a penalty of 5 marks out of 30%.
All members of the Group should come from the same Tutorial class. You may
consult and discuss the Assignment topic with others, but you must write up your
answers yourselves. Penalties for copying and plagiarism are severe.
You should follow the following typing conventions:
 Answers to be typed, in the space provided after each question
 If additional pages are required, use the blank pages at the end.
 Times New Roman font (at minimum , 12 pitch), 1.5 line spacing; and
 Left and right margins to be at least 2.5 cm from the edge of the page.
Research, Referencing and Submission
You should quote any references used at the end of each question.
Use Harvard referencing! See http://en.wikipedia.org/wiki/Harvard_referencing
As this is a calculations problem, there is no need to submit via TURNITIN.
Do not submit this page. Submit page 2 onwards, with KOI Group Assignment Cover Page.
Marking Guide
The Assignment will be scored out of 100%, in line with the rubric in the
Subject Outline. This mark will be converted to a score out of 30%.
Dr Mervyn Fiedler, Subject Co-ordinator, FIN 700. 11 August, 2017.
1

______________________________________________________________________
***NOTE:When submitting Assignment, please submit from this page onwards,
with a KOI Group Assignment cover page in front.***
Trimester T217
FIN700
GROUP ASSIGNMENT
Students: Please complete the following before submitting for marking.
Group members
Student No. Student Name Percentage Contribution to Assignment Signature
1. ………………………………………………………………………………………………
2. ………………………………………………………………………………………………
3. ………………………………………………………………………………………………
4. ………………………………………………………………………………………………
Tutor: Please circle one name: Dr Mervyn Fiedler; Ms Ruhina Karim;
Mr Masoud Ahmadi-Pirshahid; Mr Nishith Panthi.
Tutorial Day …………………………………………………and Time ……………………….
This Assignment consists of four questions. All questions must be answered.
Please answer all questions in the spaces provided after each question.
Two extra pages are included at the end of the Assignment. If more pages are
required, please copy (or extend) page 14.
2

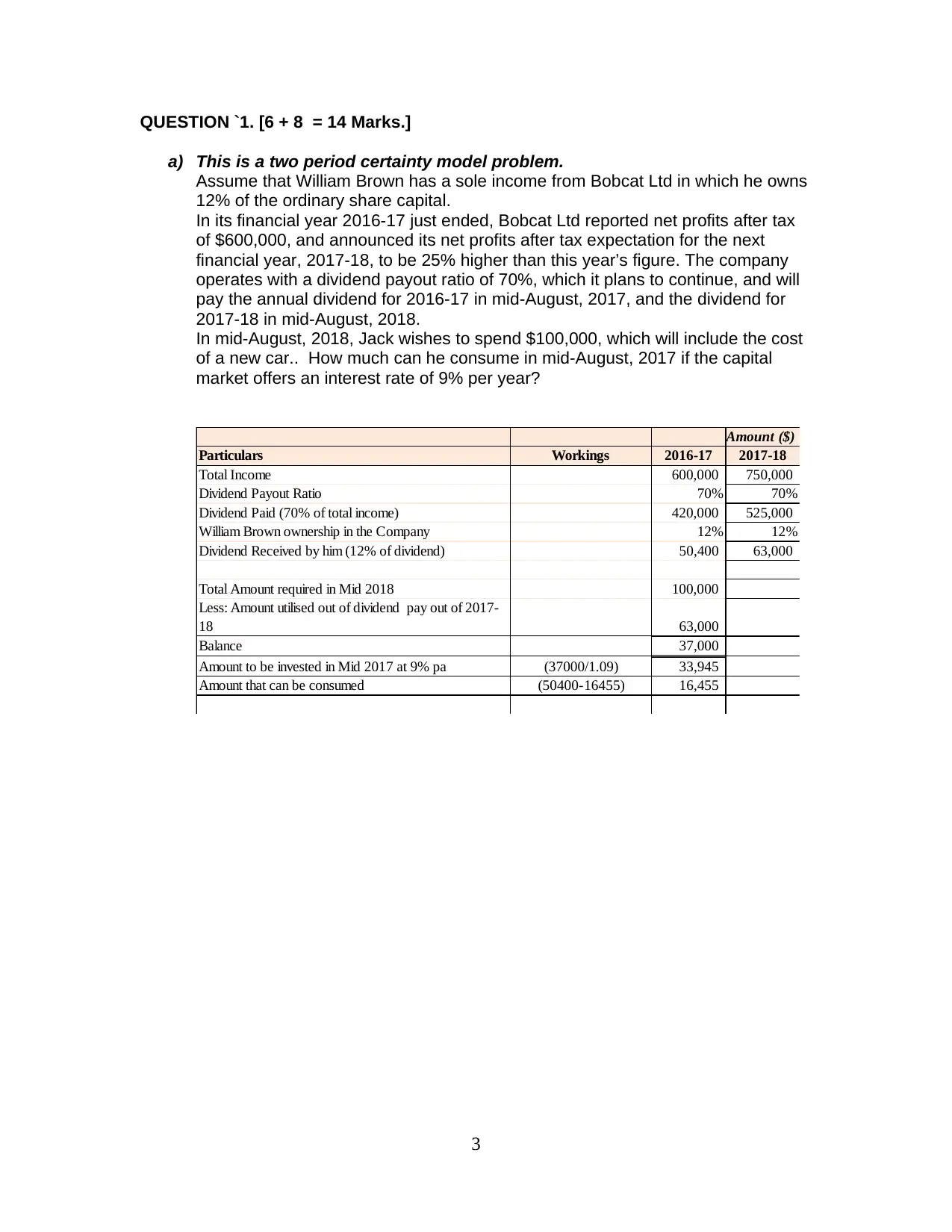
QUESTION `1. [6 + 8 = 14 Marks.]
a) This is a two period certainty model problem.
Assume that William Brown has a sole income from Bobcat Ltd in which he owns
12% of the ordinary share capital.
In its financial year 2016-17 just ended, Bobcat Ltd reported net profits after tax
of $600,000, and announced its net profits after tax expectation for the next
financial year, 2017-18, to be 25% higher than this year’s figure. The company
operates with a dividend payout ratio of 70%, which it plans to continue, and will
pay the annual dividend for 2016-17 in mid-August, 2017, and the dividend for
2017-18 in mid-August, 2018.
In mid-August, 2018, Jack wishes to spend $100,000, which will include the cost
of a new car.. How much can he consume in mid-August, 2017 if the capital
market offers an interest rate of 9% per year?
Amount ($)
Particulars Workings 2016-17 2017-18
Total Income 600,000 750,000
Dividend Payout Ratio 70% 70%
Dividend Paid (70% of total income) 420,000 525,000
William Brown ownership in the Company 12% 12%
Dividend Received by him (12% of dividend) 50,400 63,000
Total Amount required in Mid 2018 100,000
Less: Amount utilised out of dividend pay out of 2017-
18 63,000
Balance 37,000
Amount to be invested in Mid 2017 at 9% pa (37000/1.09) 33,945
Amount that can be consumed (50400-16455) 16,455
3

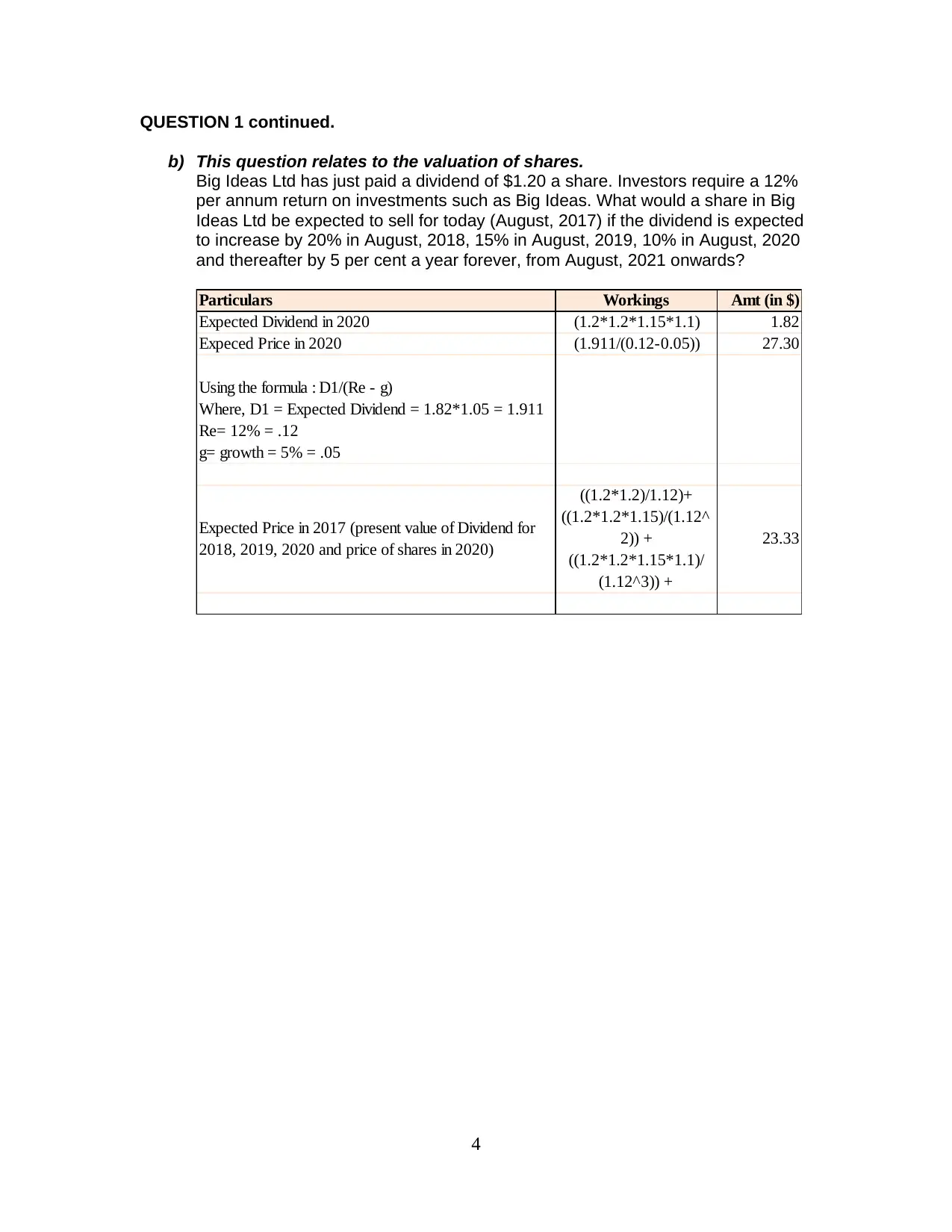
QUESTION 1 continued.
b) This question relates to the valuation of shares.
Big Ideas Ltd has just paid a dividend of $1.20 a share. Investors require a 12%
per annum return on investments such as Big Ideas. What would a share in Big
Ideas Ltd be expected to sell for today (August, 2017) if the dividend is expected
to increase by 20% in August, 2018, 15% in August, 2019, 10% in August, 2020
and thereafter by 5 per cent a year forever, from August, 2021 onwards?
Particulars Workings Amt (in $)
Expected Dividend in 2020 (1.2*1.2*1.15*1.1) 1.82
Expeced Price in 2020 (1.911/(0.12-0.05)) 27.30
Using the formula : D1/(Re - g)
Where, D1 = Expected Dividend = 1.82*1.05 = 1.911
Re= 12% = .12
g= growth = 5% = .05
Expected Price in 2017 (present value of Dividend for
2018, 2019, 2020 and price of shares in 2020)
((1.2*1.2)/1.12)+
((1.2*1.2*1.15)/(1.12^
2)) +
((1.2*1.2*1.15*1.1)/
(1.12^3)) +
23.33
4

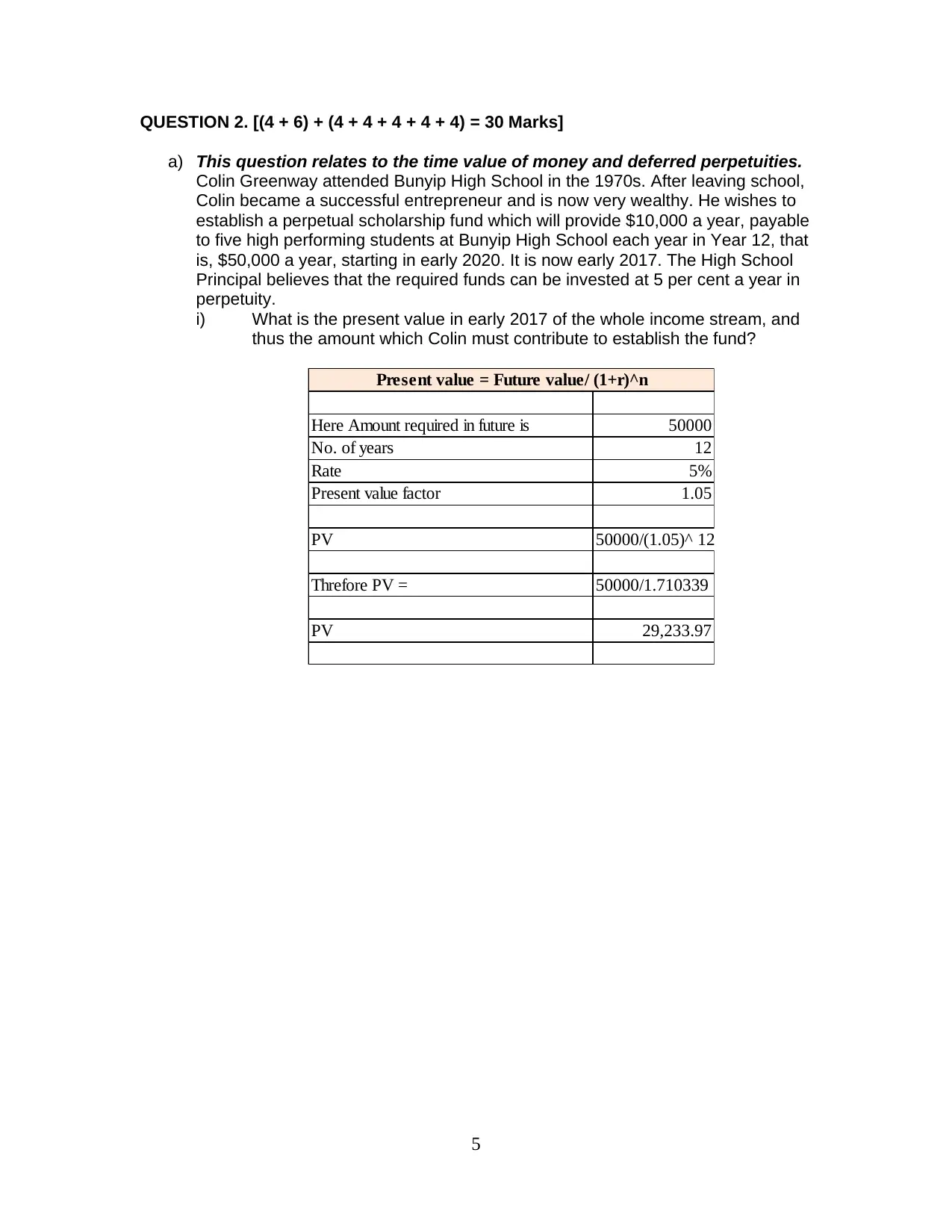
QUESTION 2. [(4 + 6) + (4 + 4 + 4 + 4 + 4) = 30 Marks]
a) This question relates to the time value of money and deferred perpetuities.
Colin Greenway attended Bunyip High School in the 1970s. After leaving school,
Colin became a successful entrepreneur and is now very wealthy. He wishes to
establish a perpetual scholarship fund which will provide $10,000 a year, payable
to five high performing students at Bunyip High School each year in Year 12, that
is, $50,000 a year, starting in early 2020. It is now early 2017. The High School
Principal believes that the required funds can be invested at 5 per cent a year in
perpetuity.
i) What is the present value in early 2017 of the whole income stream, and
thus the amount which Colin must contribute to establish the fund?
Here Amount required in future is 50000
No. of years 12
Rate 5%
Present value factor 1.05
PV 50000/(1.05)^ 12
Threfore PV = 50000/1.710339
PV 29,233.97
Present value = Future value/ (1+r)^n
5

ii) The High School Principal, while most appreciative of Colin’s great
generosity, mentions that fees at Bunyip High are rising on average by 3
per cent every year because of inflation, and that in several years,
$10,000 will not be enough to keep a student in year 12 for a whole year.
Colin decides that he will increase the amount to establish the fund so as
to provide for increases in the scholarship amount by 3 per cent a year in
perpetuity, the first increase occurring in early 2021. How much extra
(above the amount calculated in i) above, will Colin need to contribute in
early 2017 so as to provide for these inflation increases forever?
[HINT: Consider a formula similar to the dividend growth model.]
in the above case
D= 10000
Re= 5%
G= 3%
therefore
D1= 10000+10000(1.03)
10,300
therefore price of in the year 2021 103000/1.02
100,980
price of 2017 is 100980.4/(1.05)^5
100980.4/1.2155
Price = 83,077
Dividend growth modal = D1/(Re-g)
where
D1= Dividend of next year/ cashflow of upcoming year
Re= Rate of return
G= Rate of growth
6

QUESTION 2 continued.
b) This question relates to loan repayments and loan terms.
Ron and Robin Reid wish to borrow $540,000 to buy a home. The loan from
Biggles Bank requires equal monthly repayments over 20 years, and carries.an
interest rate of 7.8% per annum, compounded monthly. The first repayment is
due at the end of the first month.
You are required to calculate:
i) the effective annual interest rate on the above loan.
in this case
V= 540,000
n= 20
i= 7.80%
factor of 7.8% 1.078
So,
540000=P/.078{1-1(1+.078)^-20}
540000=P/.078{1-1/4.8416}
540000=P/.078{1-.2226}
P=540000*.78/.7774
therefore P = 541,806
Therefore
effective rate= Interest*100/principal* Time 541806*100/540000*20
5.016722222
Effective Rate = 5.01%
Value= P/i{1-(1+i)^-n}
where P= Principal, i= Rate of interest, n= No. of year
ii) the amount of the monthly repayment (consisting of interest and principal
repayment components) if the same amount is to be repaid every month
over the 20 year period of the loan.
In this case Value=12P/I {1-(1+i/12)^-12n
540000=12p/.078 (1-.8180)
12p = 540000*.078/.1818
12p = 231683
P = 231683/12
Price = 19,307
7

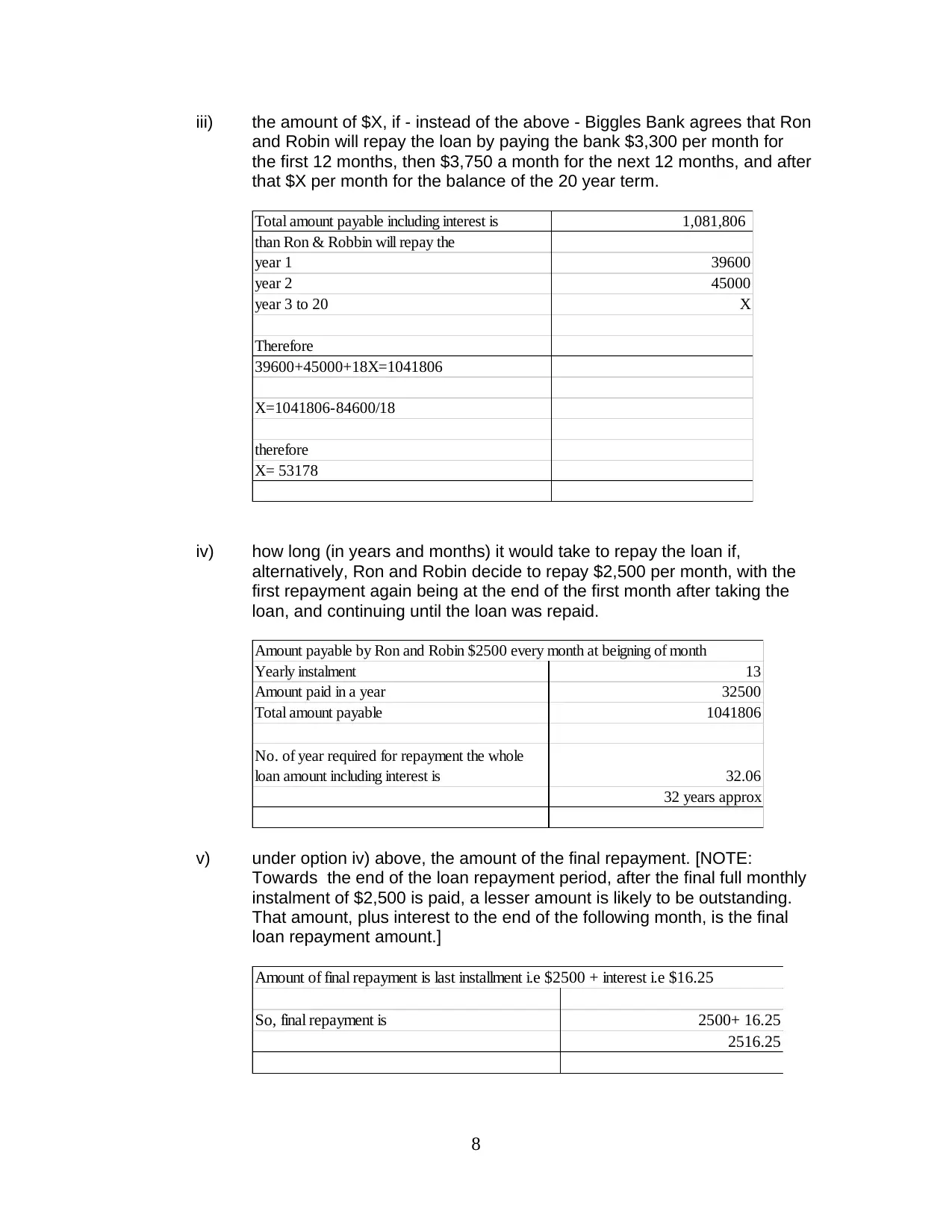
iii) the amount of $X, if - instead of the above - Biggles Bank agrees that Ron
and Robin will repay the loan by paying the bank $3,300 per month for
the first 12 months, then $3,750 a month for the next 12 months, and after
that $X per month for the balance of the 20 year term.
Total amount payable including interest is 1,081,806
than Ron & Robbin will repay the
year 1 39600
year 2 45000
year 3 to 20 X
Therefore
39600+45000+18X=1041806
X=1041806-84600/18
therefore
X= 53178
iv) how long (in years and months) it would take to repay the loan if,
alternatively, Ron and Robin decide to repay $2,500 per month, with the
first repayment again being at the end of the first month after taking the
loan, and continuing until the loan was repaid.
Yearly instalment 13
Amount paid in a year 32500
Total amount payable 1041806
No. of year required for repayment the whole
loan amount including interest is 32.06
32 years approx
Amount payable by Ron and Robin $2500 every month at beigning of month
v) under option iv) above, the amount of the final repayment. [NOTE:
Towards the end of the loan repayment period, after the final full monthly
instalment of $2,500 is paid, a lesser amount is likely to be outstanding.
That amount, plus interest to the end of the following month, is the final
loan repayment amount.]
So, final repayment is 2500+ 16.25
2516.25
Amount of final repayment is last installment i.e $2500 + interest i.e $16.25
8

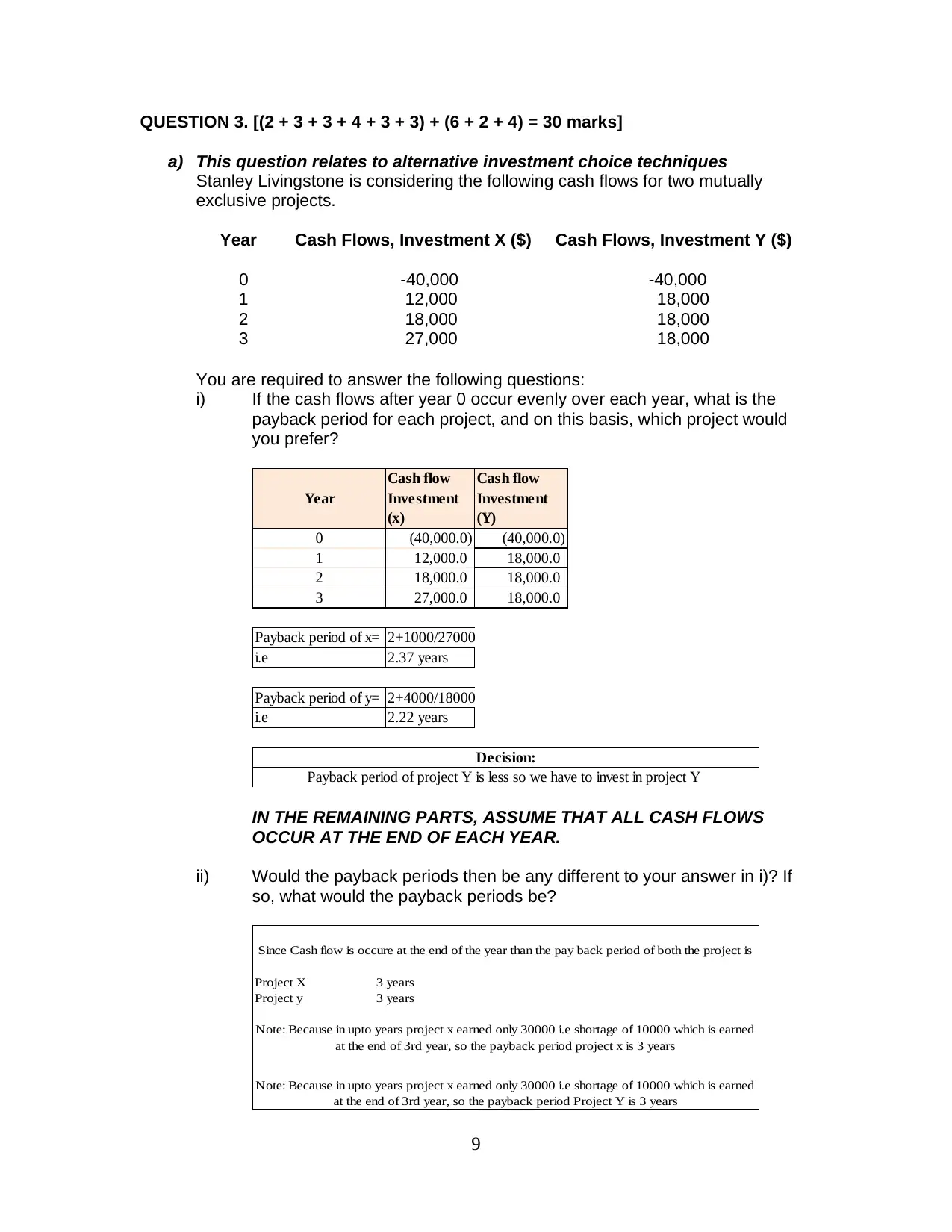
QUESTION 3. [(2 + 3 + 3 + 4 + 3 + 3) + (6 + 2 + 4) = 30 marks]
a) This question relates to alternative investment choice techniques
Stanley Livingstone is considering the following cash flows for two mutually
exclusive projects.
Year Cash Flows, Investment X ($) Cash Flows, Investment Y ($)
0 -40,000 -40,000
1 12,000 18,000
2 18,000 18,000
3 27,000 18,000
You are required to answer the following questions:
i) If the cash flows after year 0 occur evenly over each year, what is the
payback period for each project, and on this basis, which project would
you prefer?
Year
Cash flow
Investment
(x)
Cash flow
Investment
(Y)
0 (40,000.0) (40,000.0)
1 12,000.0 18,000.0
2 18,000.0 18,000.0
3 27,000.0 18,000.0
Payback period of x= 2+1000/27000
i.e 2.37 years
Payback period of y= 2+4000/18000
i.e 2.22 years
Payback period of project Y is less so we have to invest in project Y
Decision:
IN THE REMAINING PARTS, ASSUME THAT ALL CASH FLOWS
OCCUR AT THE END OF EACH YEAR.
ii) Would the payback periods then be any different to your answer in i)? If
so, what would the payback periods be?
Project X 3 years
Project y 3 years
Note: Because in upto years project x earned only 30000 i.e shortage of 10000 which is earned
at the end of 3rd year, so the payback period Project Y is 3 years
Note: Because in upto years project x earned only 30000 i.e shortage of 10000 which is earned
at the end of 3rd year, so the payback period project x is 3 years
Since Cash flow is occure at the end of the year than the pay back period of both the project is
9

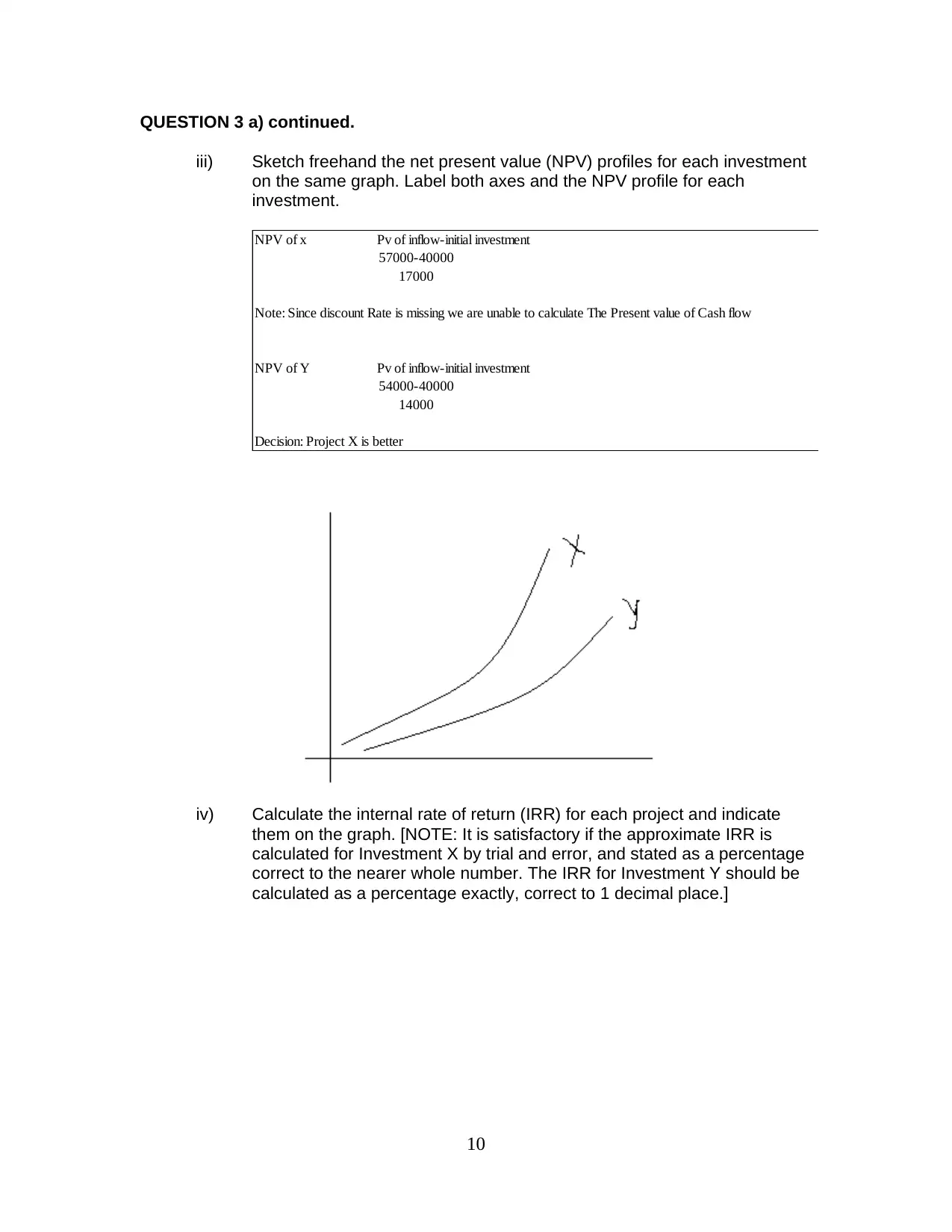
QUESTION 3 a) continued.
iii) Sketch freehand the net present value (NPV) profiles for each investment
on the same graph. Label both axes and the NPV profile for each
investment.
NPV of x Pv of inflow-initial investment
57000-40000
17000
Note: Since discount Rate is missing we are unable to calculate The Present value of Cash flow
NPV of Y Pv of inflow-initial investment
54000-40000
14000
Decision: Project X is better
iv) Calculate the internal rate of return (IRR) for each project and indicate
them on the graph. [NOTE: It is satisfactory if the approximate IRR is
calculated for Investment X by trial and error, and stated as a percentage
correct to the nearer whole number. The IRR for Investment Y should be
calculated as a percentage exactly, correct to 1 decimal place.]
10

IRR of project Y
using trial & error method using trial & error method
Let rate= 10% Let rate= 20%
40000= 12000+18000+27000 40000= 18000+18000+18000
46070 37916
Let rate= 20% Let rate= 18.5%
40000= 12000+18000+27000 40000= 18000+18000+18000
38125 38825
Let rate= 18% Let rate= 16%
40000= 18000+18000+18000
40000= 12000+18000+27000
40426
39530
Therefore IRR = Therefore IRR =
18.03% approx 16.02% approx
IRR of project x
11

QUESTION 3 a) continued.
v) Calculate the exact crossover point and indicate it on the above graph.
vi) State which of the investments you would prefer, depending on the
required rate of return (i.e., depending on the discount rate).
Result: On the basis of IRR Project X is best because IRR is higher than
the project Y
12

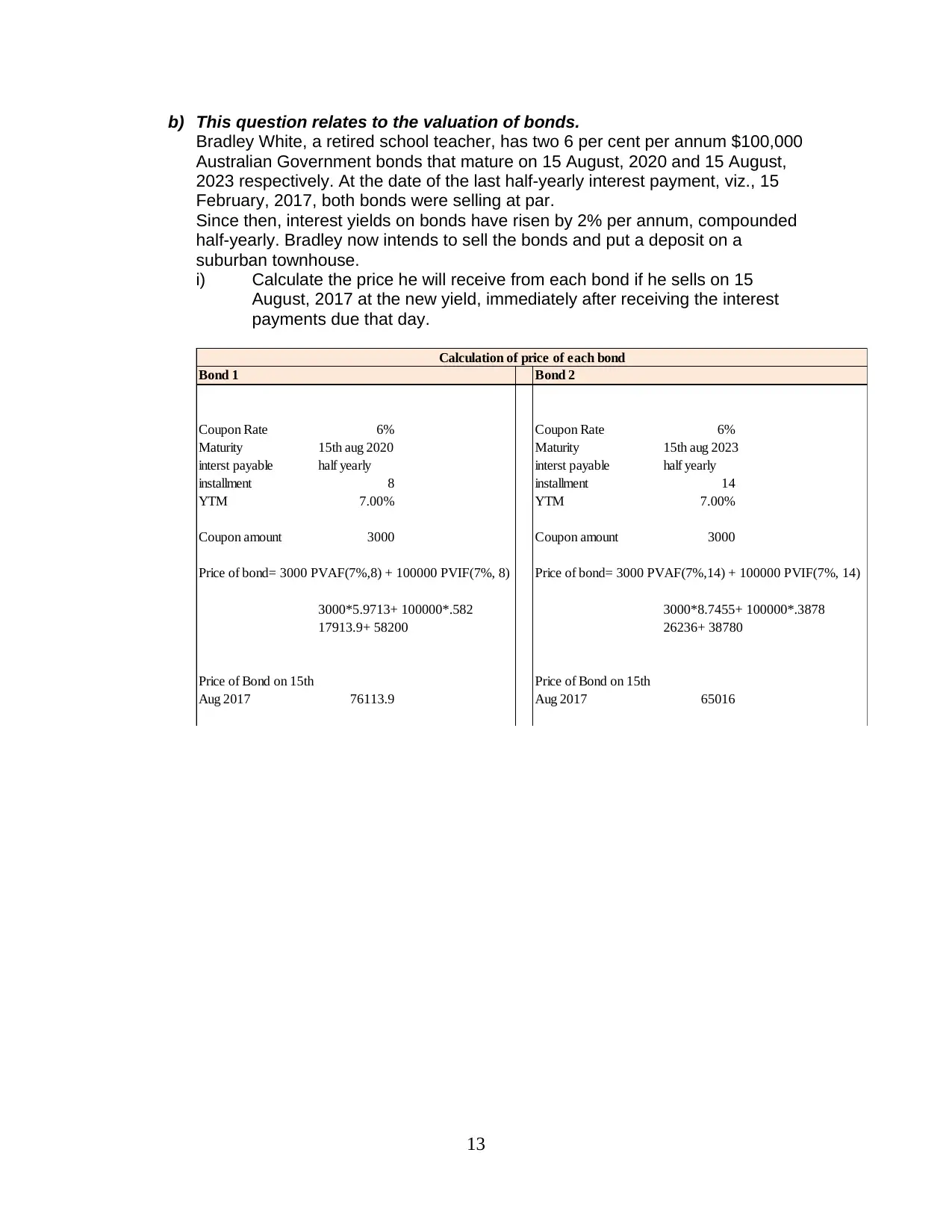
b) This question relates to the valuation of bonds.
Bradley White, a retired school teacher, has two 6 per cent per annum $100,000
Australian Government bonds that mature on 15 August, 2020 and 15 August,
2023 respectively. At the date of the last half-yearly interest payment, viz., 15
February, 2017, both bonds were selling at par.
Since then, interest yields on bonds have risen by 2% per annum, compounded
half-yearly. Bradley now intends to sell the bonds and put a deposit on a
suburban townhouse.
i) Calculate the price he will receive from each bond if he sells on 15
August, 2017 at the new yield, immediately after receiving the interest
payments due that day.
Bond 1 Bond 2
Coupon Rate 6% Coupon Rate 6%
Maturity 15th aug 2020 Maturity 15th aug 2023
interst payable half yearly interst payable half yearly
installment 8 installment 14
YTM 7.00% YTM 7.00%
Coupon amount 3000 Coupon amount 3000
Price of bond= 3000 PVAF(7%,8) + 100000 PVIF(7%, 8) Price of bond= 3000 PVAF(7%,14) + 100000 PVIF(7%, 14)
3000*5.9713+ 100000*.582 3000*8.7455+ 100000*.3878
17913.9+ 58200 26236+ 38780
Price of Bond on 15th
Aug 2017 76113.9
Price of Bond on 15th
Aug 2017 65016
Calculation of price of each bond
13

QUESTION 3 b) continued.
ii) Explain the relative price movements in the two bonds, as evidenced in
your answer to i) above.
Duration= CY/YTM*PVAF (YTM,N) (1+YTM) + (1-CY/YTM)N
Current yeid (CY)= Coupoun amount/ market price *100
Bond 1
CY 3.941461415
YTM 7
D= 3.94/7* PVAF(7%, 8)(1.07)+ (1-3.94/7)8
.568*5.9713*1.07+3.52
3.63+3.52
7.15
Duration = 7.15 years
Bond 2
CY 4.6142488
YTM 7
D= 4.61/7* PVAF(7%, 14)(1.07)+ (1-4.61/7)14
.659*8.7455*1.07+4.788
6.166+4.788
10.95
Duration = 10.95 years
Relative price movement (Duration) of bond
iii) Suppose that Bradley defers buying the bonds for 84 days, that is until 7
November, 2017. How much will he pay for each bond on that day?
[NOTE: Between the bond interest due dates from mid-August to mid-
February is 184 days, during which time interest accrues on a compound
basis.]
Extra amount paid if bond buy on 7th november
Bond 1 10000*3%/184*84
Interest of 84 days 1370
extra amount paid if bond buy on 7th november 2017 i. e 1370
Amount paid for Bond 1 is =76113.9+1370
77483.9
Amount paid for Bond 2 is =65016+1370
66386
14

QUESTION 4. [24 + 2 = 26 marks].
This question relates to capital budgeting.
Perth Projects Ltd is considering the purchase of new technology costing $600,000,
which it will fully finance with a fixed interest loan of 10% per annum, with the principal
repaid at the end of 4 years.
The new technology will permit the company to reduce its to reduce its labour costs by
$200,000 a year for 4 years, and the technology may be depreciated for tax purposes by
the straight-line method to zero over the 4 years. The company thinks that it can sell the
technology at the end of 4 years for $30,000.
The technology will need to be stored in a building, currently being rented out for
$40,000 a year under a lease agreement with 4 yearly rental payments to run, the next
one being due at the end of one year. Under the lease agreement, Perth Projects Ltd
can cancel the lease by paying the tenant (now) compensation equal to one year’s rental
payment plus 10%, but this amount is not deductible for income tax purposes.
This is not the first time that the company has considered this purchase. Twelve months
ago, the company engaged Marvel Consultants, at a fee of $30,000 paid in advance, to
conduct a feasibility study on savings strategies and Marvel made the above
recommendations. At the time, Perth Projects did not proceed with the recommended
strategy, but is now reconsidering the proposal.
Perth Projects further estimates that it will have to spend $20,000 in 2 years’ time
overhauling the technology. It will also require additions to current assets of $30,000 at
the beginning of the project, which will be fully recoverable at the end of the fourth year.
Perth Projects Ltd’s cost of capital is 10%. The tax rate is 30%. Tax is paid in the year in
which earnings are received.
REQUIRED:
(a) Calculate the net present value (NPV), that is, the net benefit or net loss in
present value terms of the proposed purchase costs and the resultant
incremental cash flows.
[HINT: As shown in the text-book, it is recommended that for each year you
calculate the tax effect first, then identify the cash flows, then calculate the
overall net present value.
15

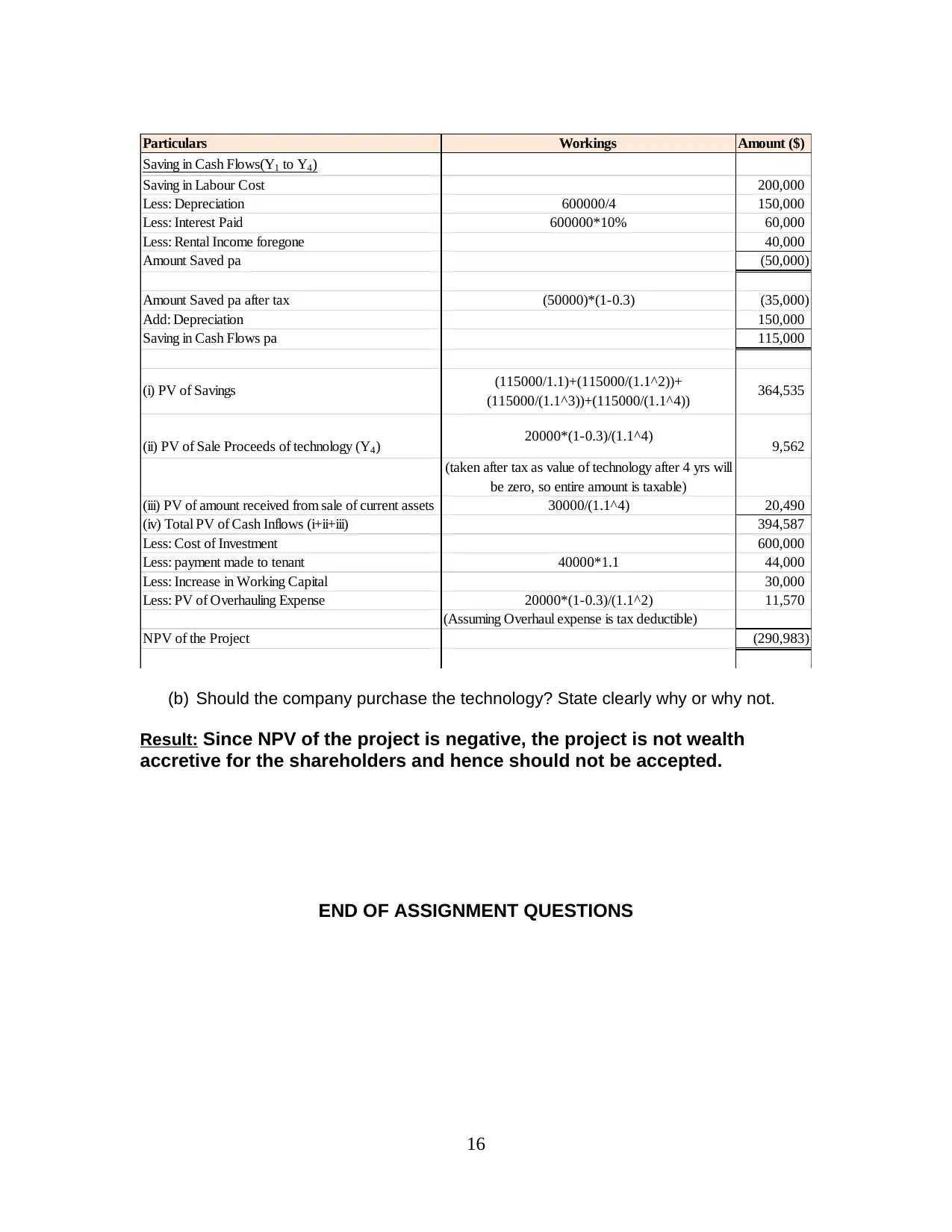
Particulars Workings Amount ($)
Saving in Cash Flows(Y1 to Y4 )
Saving in Labour Cost 200,000
Less: Depreciation 600000/4 150,000
Less: Interest Paid 600000*10% 60,000
Less: Rental Income foregone 40,000
Amount Saved pa (50,000)
Amount Saved pa after tax (50000)*(1-0.3) (35,000)
Add: Depreciation 150,000
Saving in Cash Flows pa 115,000
(i) PV of Savings (115000/1.1)+(115000/(1.1^2))+
(115000/(1.1^3))+(115000/(1.1^4)) 364,535
(ii) PV of Sale Proceeds of technology (Y4 ) 20000*(1-0.3)/(1.1^4) 9,562
(taken after tax as value of technology after 4 yrs will
be zero, so entire amount is taxable)
(iii) PV of amount received from sale of current assets 30000/(1.1^4) 20,490
(iv) Total PV of Cash Inflows (i+ii+iii) 394,587
Less: Cost of Investment 600,000
Less: payment made to tenant 40000*1.1 44,000
Less: Increase in Working Capital 30,000
Less: PV of Overhauling Expense 20000*(1-0.3)/(1.1^2) 11,570
(Assuming Overhaul expense is tax deductible)
NPV of the Project (290,983)
(b) Should the company purchase the technology? State clearly why or why not.
Result: Since NPV of the project is negative, the project is not wealth
accretive for the shareholders and hence should not be accepted.
END OF ASSIGNMENT QUESTIONS
16