Finance Assignment: Financial Valuation, Investment, and Loan Analysis
VerifiedAdded on 2020/03/04
|14
|3299
|87
Homework Assignment
AI Summary
This finance assignment provides detailed solutions to complex financial problems. The assignment covers a range of topics including the two-period certainty model, share valuation, time value of money, deferred perpetuities, loan repayments, and investment choice techniques. It includes calculations for dividends, present value, internal rate of return (IRR), net present value (NPV), bond valuation, and loan amortization schedules. The solutions demonstrate the application of financial formulas and concepts to real-world scenarios, such as investment projects, loan terms, and bond valuation, offering a comprehensive understanding of financial analysis. The assignment includes step-by-step calculations and explanations to help students understand the concepts and problem-solving techniques.

QUESTION `1. [6 + 8 = 14 Marks.]
a) This is a two period certainty model problem.
Assume that William Brown has a sole income from Bobcat Ltd in which he owns
12% of the ordinary share capital.
In its financial year 2016-17 just ended, Bobcat Ltd reported net profits after tax of
$600,000, and announced its net profits after tax expectation for the next financial
year, 2017-18, to be 25% higher than this year’s figure. The company operates with a
dividend payout ratio of 70%, which it plans to continue, and will pay the annual
dividend for 2016-17 in mid-August, 2017, and the dividend for 2017-18 in mid-
August, 2018.
In mid-August, 2018, Jack wishes to spend $100,000, which will include the cost of a
new car.. How much can he consume in mid-August, 2017 if the capital market offers
an interest rate of 9% per year?
Answer:
Dividend payable in Aug. 2017 = Net profits after tax * dividend payout ratio
= $6, 00,000 * 70%
= $4, 20,000
Dividends available to Jack = $4,20,000 * 12%
= $50,400
Net profits after tax in 2018 = $6,00,000 * 1.25
= $7,50,000
Dividend payable in Aug. 2017 = 7,50,000 * 70%
= $5,25,000
Dividends to be available to Jack in 2018 = $5,25,000 * 12%
= $63,000
Present value of dividend = dividend payable in 2018 / (1+rate of interest)^1
= 63000 / 1.09^1
= $57,798.2
Hence total amount available with Jack = $50,400 + $57,798.2
= $1,08,198.16
a) This is a two period certainty model problem.
Assume that William Brown has a sole income from Bobcat Ltd in which he owns
12% of the ordinary share capital.
In its financial year 2016-17 just ended, Bobcat Ltd reported net profits after tax of
$600,000, and announced its net profits after tax expectation for the next financial
year, 2017-18, to be 25% higher than this year’s figure. The company operates with a
dividend payout ratio of 70%, which it plans to continue, and will pay the annual
dividend for 2016-17 in mid-August, 2017, and the dividend for 2017-18 in mid-
August, 2018.
In mid-August, 2018, Jack wishes to spend $100,000, which will include the cost of a
new car.. How much can he consume in mid-August, 2017 if the capital market offers
an interest rate of 9% per year?
Answer:
Dividend payable in Aug. 2017 = Net profits after tax * dividend payout ratio
= $6, 00,000 * 70%
= $4, 20,000
Dividends available to Jack = $4,20,000 * 12%
= $50,400
Net profits after tax in 2018 = $6,00,000 * 1.25
= $7,50,000
Dividend payable in Aug. 2017 = 7,50,000 * 70%
= $5,25,000
Dividends to be available to Jack in 2018 = $5,25,000 * 12%
= $63,000
Present value of dividend = dividend payable in 2018 / (1+rate of interest)^1
= 63000 / 1.09^1
= $57,798.2
Hence total amount available with Jack = $50,400 + $57,798.2
= $1,08,198.16
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Jack needs to spend $100000 in mid August, hence the amount he can consume today will be
the amount present value of amount available with Jack in 2017 less $100000.
= $1,08,198.16 - $100,000
= $8,198.16
QUESTION 1 continued.
b) This question relates to the valuation of shares.
Big Ideas Ltd has just paid a dividend of $1.20 a share. Investors require a 12% per
annum return on investments such as Big Ideas. What would a share in Big Ideas Ltd
be expected to sell for today (August, 2017) if the dividend is expected to increase by
20% in August, 2018, 15% in August, 2019, 10% in August, 2020 and thereafter by 5
per cent a year forever, from August, 2021 onwards?
Answer:
Year Dividend growth rate Expected dividend
2017 $1.2
2018 20% $1.44
2019 15% $1.65
2020 10% $1.82
2021 5% $1.91
Price of share in year 2020 = expected dividend / (rate of return – growth rate)
= 1.91 / (0.12-0.05)
= $27.32
Price of share in 2017 = D1 / (1+r)^1 + D2 / (1+r)^2 + D3 / (1+r)^3 + P4 / (1+r)^4
= 1.44 / 1.12^1 + 1.65 / 1.12^2 + 1.82 / 1.12^3 + 27.32 / 1.12^3
= $1.28 + $1.31 + $1.29+ $19.44
= $23.32
Question 2
a) This question relates to the time value of money and deferred perpetuities.
the amount present value of amount available with Jack in 2017 less $100000.
= $1,08,198.16 - $100,000
= $8,198.16
QUESTION 1 continued.
b) This question relates to the valuation of shares.
Big Ideas Ltd has just paid a dividend of $1.20 a share. Investors require a 12% per
annum return on investments such as Big Ideas. What would a share in Big Ideas Ltd
be expected to sell for today (August, 2017) if the dividend is expected to increase by
20% in August, 2018, 15% in August, 2019, 10% in August, 2020 and thereafter by 5
per cent a year forever, from August, 2021 onwards?
Answer:
Year Dividend growth rate Expected dividend
2017 $1.2
2018 20% $1.44
2019 15% $1.65
2020 10% $1.82
2021 5% $1.91
Price of share in year 2020 = expected dividend / (rate of return – growth rate)
= 1.91 / (0.12-0.05)
= $27.32
Price of share in 2017 = D1 / (1+r)^1 + D2 / (1+r)^2 + D3 / (1+r)^3 + P4 / (1+r)^4
= 1.44 / 1.12^1 + 1.65 / 1.12^2 + 1.82 / 1.12^3 + 27.32 / 1.12^3
= $1.28 + $1.31 + $1.29+ $19.44
= $23.32
Question 2
a) This question relates to the time value of money and deferred perpetuities.

Colin Greenway attended Bunyip High School in the 1970s. After leaving school,
Colin became a successful entrepreneur and is now very wealthy. He wishes to
establish a perpetual scholarship fund which will provide $10,000 a year, payable to
five high performing students at Bunyip High School each year in Year 12, that is,
$50,000 a year, starting in early 2020. It is now early 2017. The High School
Principal believes that the required funds can be invested at 5 per cent a year in
perpetuity.
i) What is the present value in early 2017 of the whole income stream, and thus
the amount which Colin must contribute to establish the fund?
Answer:
PVof perpetuity in 2020 = C1 / r
= 50000 / 0.05
= $10,00,000
PV of perpetuity in 2017 = PV2020 / (1+r)^3
= 1000000 / 1.05^3
= $ 8,63,837.6
ii) The High School Principal, while most appreciative of Colin’s great
generosity, mentions that fees at Bunyip High are rising on average by 3 per
cent every year because of inflation, and that in several years, $10,000 will not
be enough to keep a student in year 12 for a whole year. Colin decides that he
will increase the amount to establish the fund so as to provide for increases in
the scholarship amount by 3 per cent a year in perpetuity, the first increase
occurring in early 2021. How much extra (above the amount calculated in i)
above, will Colin need to contribute in early 2017 so as to provide for these
inflation increases forever?
[HINT: Consider a formula similar to the dividend growth model.]
Answer:
Colin became a successful entrepreneur and is now very wealthy. He wishes to
establish a perpetual scholarship fund which will provide $10,000 a year, payable to
five high performing students at Bunyip High School each year in Year 12, that is,
$50,000 a year, starting in early 2020. It is now early 2017. The High School
Principal believes that the required funds can be invested at 5 per cent a year in
perpetuity.
i) What is the present value in early 2017 of the whole income stream, and thus
the amount which Colin must contribute to establish the fund?
Answer:
PVof perpetuity in 2020 = C1 / r
= 50000 / 0.05
= $10,00,000
PV of perpetuity in 2017 = PV2020 / (1+r)^3
= 1000000 / 1.05^3
= $ 8,63,837.6
ii) The High School Principal, while most appreciative of Colin’s great
generosity, mentions that fees at Bunyip High are rising on average by 3 per
cent every year because of inflation, and that in several years, $10,000 will not
be enough to keep a student in year 12 for a whole year. Colin decides that he
will increase the amount to establish the fund so as to provide for increases in
the scholarship amount by 3 per cent a year in perpetuity, the first increase
occurring in early 2021. How much extra (above the amount calculated in i)
above, will Colin need to contribute in early 2017 so as to provide for these
inflation increases forever?
[HINT: Consider a formula similar to the dividend growth model.]
Answer:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
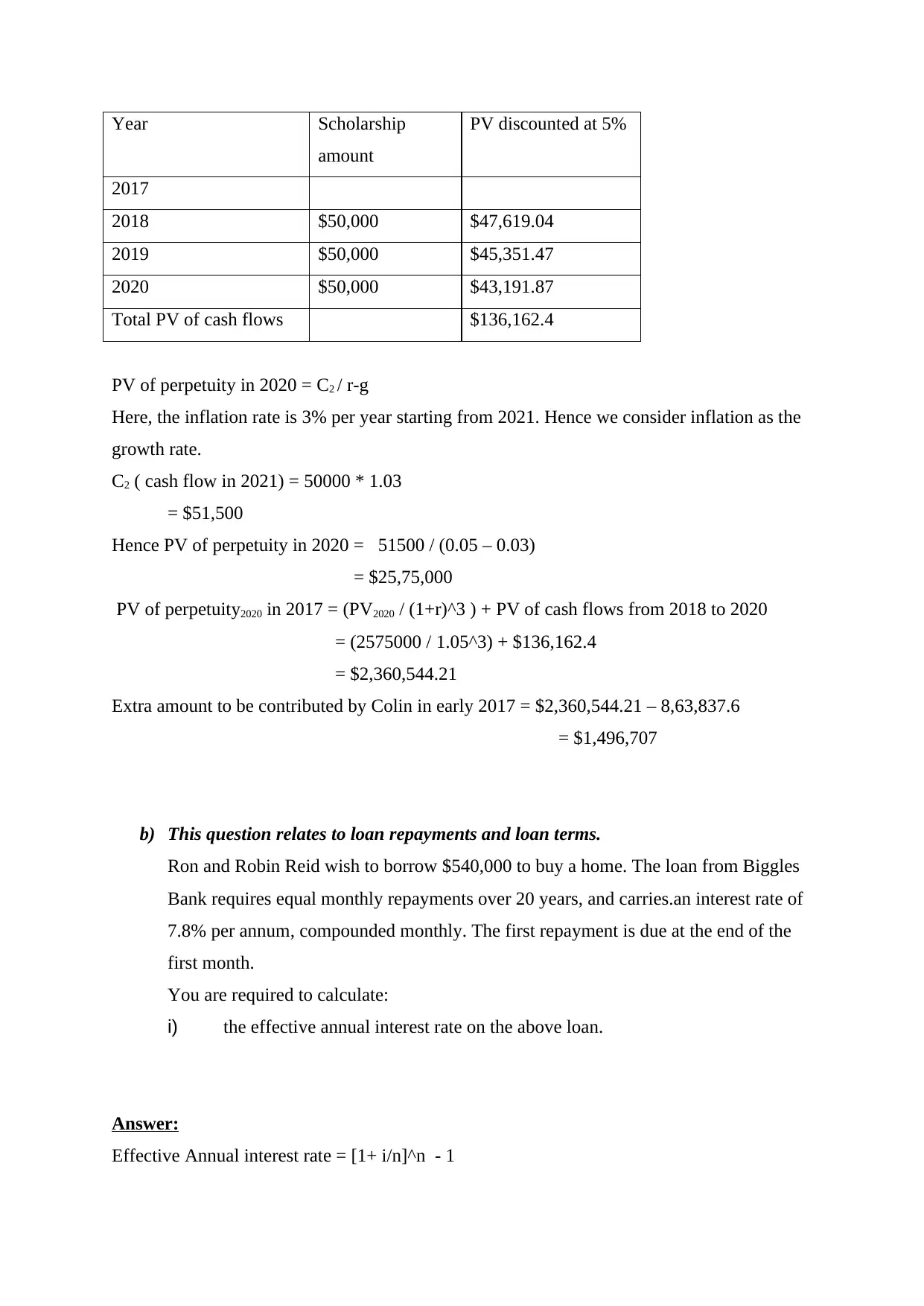
Year Scholarship
amount
PV discounted at 5%
2017
2018 $50,000 $47,619.04
2019 $50,000 $45,351.47
2020 $50,000 $43,191.87
Total PV of cash flows $136,162.4
PV of perpetuity in 2020 = C2 / r-g
Here, the inflation rate is 3% per year starting from 2021. Hence we consider inflation as the
growth rate.
C2 ( cash flow in 2021) = 50000 * 1.03
= $51,500
Hence PV of perpetuity in 2020 = 51500 / (0.05 – 0.03)
= $25,75,000
PV of perpetuity2020 in 2017 = (PV2020 / (1+r)^3 ) + PV of cash flows from 2018 to 2020
= (2575000 / 1.05^3) + $136,162.4
= $2,360,544.21
Extra amount to be contributed by Colin in early 2017 = $2,360,544.21 – 8,63,837.6
= $1,496,707
b) This question relates to loan repayments and loan terms.
Ron and Robin Reid wish to borrow $540,000 to buy a home. The loan from Biggles
Bank requires equal monthly repayments over 20 years, and carries.an interest rate of
7.8% per annum, compounded monthly. The first repayment is due at the end of the
first month.
You are required to calculate:
i) the effective annual interest rate on the above loan.
Answer:
Effective Annual interest rate = [1+ i/n]^n - 1
amount
PV discounted at 5%
2017
2018 $50,000 $47,619.04
2019 $50,000 $45,351.47
2020 $50,000 $43,191.87
Total PV of cash flows $136,162.4
PV of perpetuity in 2020 = C2 / r-g
Here, the inflation rate is 3% per year starting from 2021. Hence we consider inflation as the
growth rate.
C2 ( cash flow in 2021) = 50000 * 1.03
= $51,500
Hence PV of perpetuity in 2020 = 51500 / (0.05 – 0.03)
= $25,75,000
PV of perpetuity2020 in 2017 = (PV2020 / (1+r)^3 ) + PV of cash flows from 2018 to 2020
= (2575000 / 1.05^3) + $136,162.4
= $2,360,544.21
Extra amount to be contributed by Colin in early 2017 = $2,360,544.21 – 8,63,837.6
= $1,496,707
b) This question relates to loan repayments and loan terms.
Ron and Robin Reid wish to borrow $540,000 to buy a home. The loan from Biggles
Bank requires equal monthly repayments over 20 years, and carries.an interest rate of
7.8% per annum, compounded monthly. The first repayment is due at the end of the
first month.
You are required to calculate:
i) the effective annual interest rate on the above loan.
Answer:
Effective Annual interest rate = [1+ i/n]^n - 1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

i = 7.8%
n = 12
hence, EAR = [1+ 0.078/12]^12 - 1
= 8.08%
ii) the amount of the monthly repayment (consisting of interest and principal
repayment components) if the same amount is to be repaid every month over
the 20 year period of the loan.
Answer:
PMT = Pi / (1-(1+i)^-n)
P = $540,000
I = 7.8% / 12 = 0.7%
N = 20*12 = 240
PMT = (540000*0.0065) / (1-(1.0065)^-240)
= 3510 / 0.788
= $4,449.7
Hence a monthly repayment of $4,449.7 is to be repaid every month for the 20 year loan
period.
iii) the amount of $X, if - instead of the above - Biggles Bank agrees that Ron and
Robin will repay the loan by paying the bank $3,300 per month for the first 12
months, then $3,750 a month for the next 12 months, and after that $X per
month for the balance of the 20 year term.
Answer:
PV of annuity = C * [(1-(1+i)^-n) / i]
PV of $3300 to be paid for first 12 months = 3300 * [(1-1.0065^-12) / 0.0065]
n = 12
hence, EAR = [1+ 0.078/12]^12 - 1
= 8.08%
ii) the amount of the monthly repayment (consisting of interest and principal
repayment components) if the same amount is to be repaid every month over
the 20 year period of the loan.
Answer:
PMT = Pi / (1-(1+i)^-n)
P = $540,000
I = 7.8% / 12 = 0.7%
N = 20*12 = 240
PMT = (540000*0.0065) / (1-(1.0065)^-240)
= 3510 / 0.788
= $4,449.7
Hence a monthly repayment of $4,449.7 is to be repaid every month for the 20 year loan
period.
iii) the amount of $X, if - instead of the above - Biggles Bank agrees that Ron and
Robin will repay the loan by paying the bank $3,300 per month for the first 12
months, then $3,750 a month for the next 12 months, and after that $X per
month for the balance of the 20 year term.
Answer:
PV of annuity = C * [(1-(1+i)^-n) / i]
PV of $3300 to be paid for first 12 months = 3300 * [(1-1.0065^-12) / 0.0065]

= $37,976.43
PV of $3750 to be paid for next 12 months = 3750 * [(1-1.0065^-12) / 0.0065]
= $43,155.04
PV of deferred annuity = 43155.04 / (1.0065)^12
= $39,926.96
PV of payments made in 2 years = $37,976.43 + $39,926.96
= $77,903.4
Total amount to be paid by end of 20 years = 4,449.7 * 240 = $10,67,928
Hence, balance amount to be paid = $10,67,928 - $77,903.4
= $9,90,025
Let X be the amount to be paid per month for the rest of the period
PV of annuity for 18 years = X * [(1-1.0065^-216) / 0.0065]
= 115.88 X
PV of deferred annuity = 115.88X / (1.0065^24)
990025 = 115.88X / 1.17
X = $9,980.86
Hence, an installment of $9980.8 will be paid after two years for a period of 18 years.
iv) how long (in years and months) it would take to repay the loan if,
alternatively, Ron and Robin decide to repay $2,500 per month, with the first
repayment again being at the end of the first month after taking the loan, and
continuing until the loan was repaid.
Answer:
The question has given the loan installment of $2500 which is not possible because the
monthly interest on the loan itself is $3,510; hence we are assuming a print mistake and
taking the installment as $25,000.
25000 = (540000*0.0065) / (1-(1.0065)^-n)
25000 = 3510 / (1-(1.0065)^-n)
1-(1.0065) ^-n = 0.14
PV of $3750 to be paid for next 12 months = 3750 * [(1-1.0065^-12) / 0.0065]
= $43,155.04
PV of deferred annuity = 43155.04 / (1.0065)^12
= $39,926.96
PV of payments made in 2 years = $37,976.43 + $39,926.96
= $77,903.4
Total amount to be paid by end of 20 years = 4,449.7 * 240 = $10,67,928
Hence, balance amount to be paid = $10,67,928 - $77,903.4
= $9,90,025
Let X be the amount to be paid per month for the rest of the period
PV of annuity for 18 years = X * [(1-1.0065^-216) / 0.0065]
= 115.88 X
PV of deferred annuity = 115.88X / (1.0065^24)
990025 = 115.88X / 1.17
X = $9,980.86
Hence, an installment of $9980.8 will be paid after two years for a period of 18 years.
iv) how long (in years and months) it would take to repay the loan if,
alternatively, Ron and Robin decide to repay $2,500 per month, with the first
repayment again being at the end of the first month after taking the loan, and
continuing until the loan was repaid.
Answer:
The question has given the loan installment of $2500 which is not possible because the
monthly interest on the loan itself is $3,510; hence we are assuming a print mistake and
taking the installment as $25,000.
25000 = (540000*0.0065) / (1-(1.0065)^-n)
25000 = 3510 / (1-(1.0065)^-n)
1-(1.0065) ^-n = 0.14
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

n = 24
hence number of years taken to repay the loan = 2 years
v) under option iv) above, the amount of the final repayment. [NOTE: Towards
the end of the loan repayment period, after the final full monthly instalment of
$2,500 is paid, a lesser amount is likely to be outstanding. That amount, plus
interest to the end of the following month, is the final loan repayment
amount.]
Answer:
The full payment has been made in the last month of the second year. Hence, there is no
amount outstanding in the following month.
Question 3
a) This question relates to alternative investment choice techniques
Stanley Livingstone is considering the following cash flows for two mutually
exclusive projects.
Year Cash Flows, Investment X ($) Cash Flows, Investment Y ($)
0 -40,000 -40,000
1 12,000 18,000
2 18,000 18,000
3 27,000 18,000
You are required to answer the following questions:
i) If the cash flows after year 0 occur evenly over each year, what is the payback
period for each project, and on this basis, which project would you prefer?
Answer:
hence number of years taken to repay the loan = 2 years
v) under option iv) above, the amount of the final repayment. [NOTE: Towards
the end of the loan repayment period, after the final full monthly instalment of
$2,500 is paid, a lesser amount is likely to be outstanding. That amount, plus
interest to the end of the following month, is the final loan repayment
amount.]
Answer:
The full payment has been made in the last month of the second year. Hence, there is no
amount outstanding in the following month.
Question 3
a) This question relates to alternative investment choice techniques
Stanley Livingstone is considering the following cash flows for two mutually
exclusive projects.
Year Cash Flows, Investment X ($) Cash Flows, Investment Y ($)
0 -40,000 -40,000
1 12,000 18,000
2 18,000 18,000
3 27,000 18,000
You are required to answer the following questions:
i) If the cash flows after year 0 occur evenly over each year, what is the payback
period for each project, and on this basis, which project would you prefer?
Answer:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
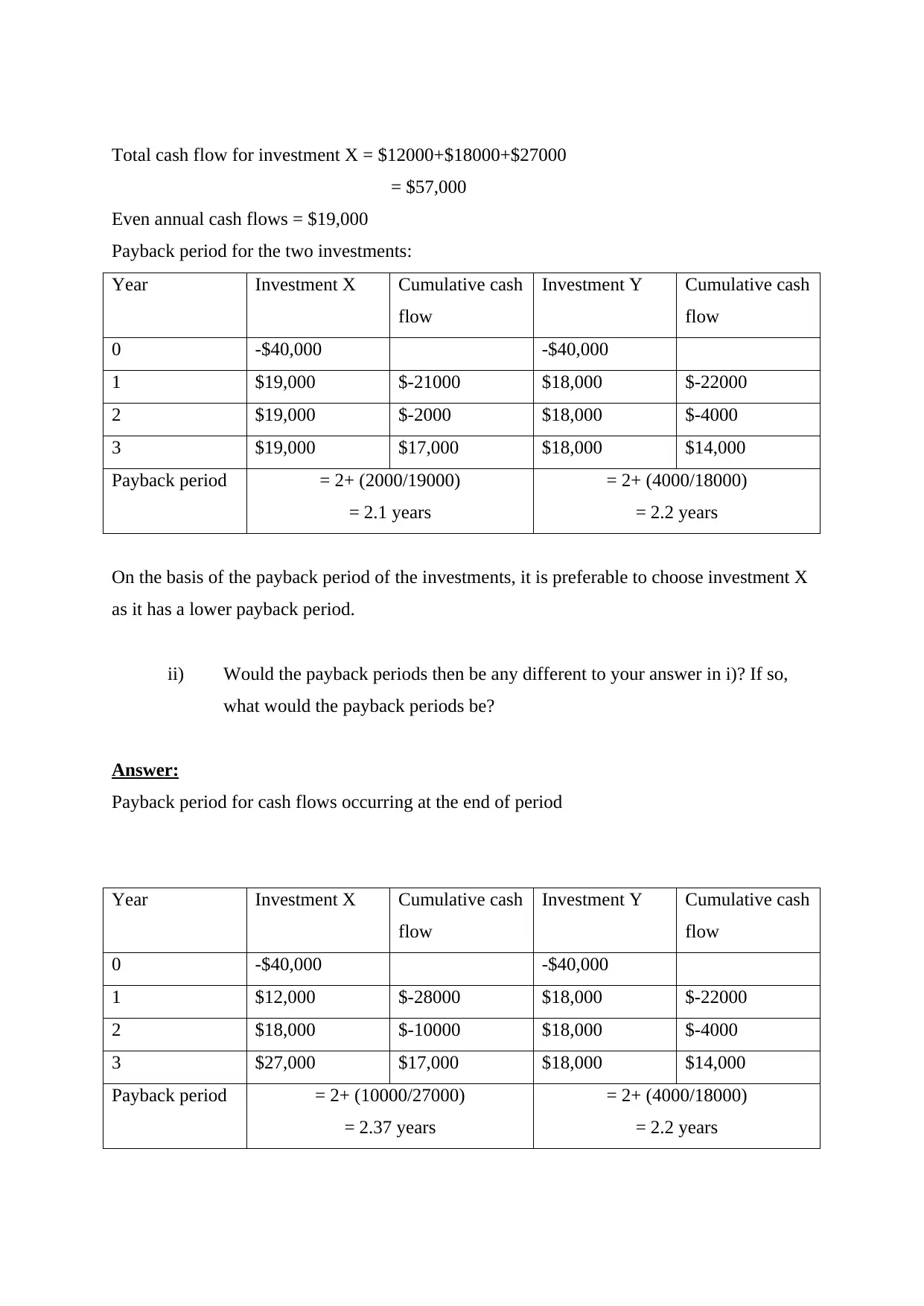
Total cash flow for investment X = $12000+$18000+$27000
= $57,000
Even annual cash flows = $19,000
Payback period for the two investments:
Year Investment X Cumulative cash
flow
Investment Y Cumulative cash
flow
0 -$40,000 -$40,000
1 $19,000 $-21000 $18,000 $-22000
2 $19,000 $-2000 $18,000 $-4000
3 $19,000 $17,000 $18,000 $14,000
Payback period = 2+ (2000/19000)
= 2.1 years
= 2+ (4000/18000)
= 2.2 years
On the basis of the payback period of the investments, it is preferable to choose investment X
as it has a lower payback period.
ii) Would the payback periods then be any different to your answer in i)? If so,
what would the payback periods be?
Answer:
Payback period for cash flows occurring at the end of period
Year Investment X Cumulative cash
flow
Investment Y Cumulative cash
flow
0 -$40,000 -$40,000
1 $12,000 $-28000 $18,000 $-22000
2 $18,000 $-10000 $18,000 $-4000
3 $27,000 $17,000 $18,000 $14,000
Payback period = 2+ (10000/27000)
= 2.37 years
= 2+ (4000/18000)
= 2.2 years
= $57,000
Even annual cash flows = $19,000
Payback period for the two investments:
Year Investment X Cumulative cash
flow
Investment Y Cumulative cash
flow
0 -$40,000 -$40,000
1 $19,000 $-21000 $18,000 $-22000
2 $19,000 $-2000 $18,000 $-4000
3 $19,000 $17,000 $18,000 $14,000
Payback period = 2+ (2000/19000)
= 2.1 years
= 2+ (4000/18000)
= 2.2 years
On the basis of the payback period of the investments, it is preferable to choose investment X
as it has a lower payback period.
ii) Would the payback periods then be any different to your answer in i)? If so,
what would the payback periods be?
Answer:
Payback period for cash flows occurring at the end of period
Year Investment X Cumulative cash
flow
Investment Y Cumulative cash
flow
0 -$40,000 -$40,000
1 $12,000 $-28000 $18,000 $-22000
2 $18,000 $-10000 $18,000 $-4000
3 $27,000 $17,000 $18,000 $14,000
Payback period = 2+ (10000/27000)
= 2.37 years
= 2+ (4000/18000)
= 2.2 years
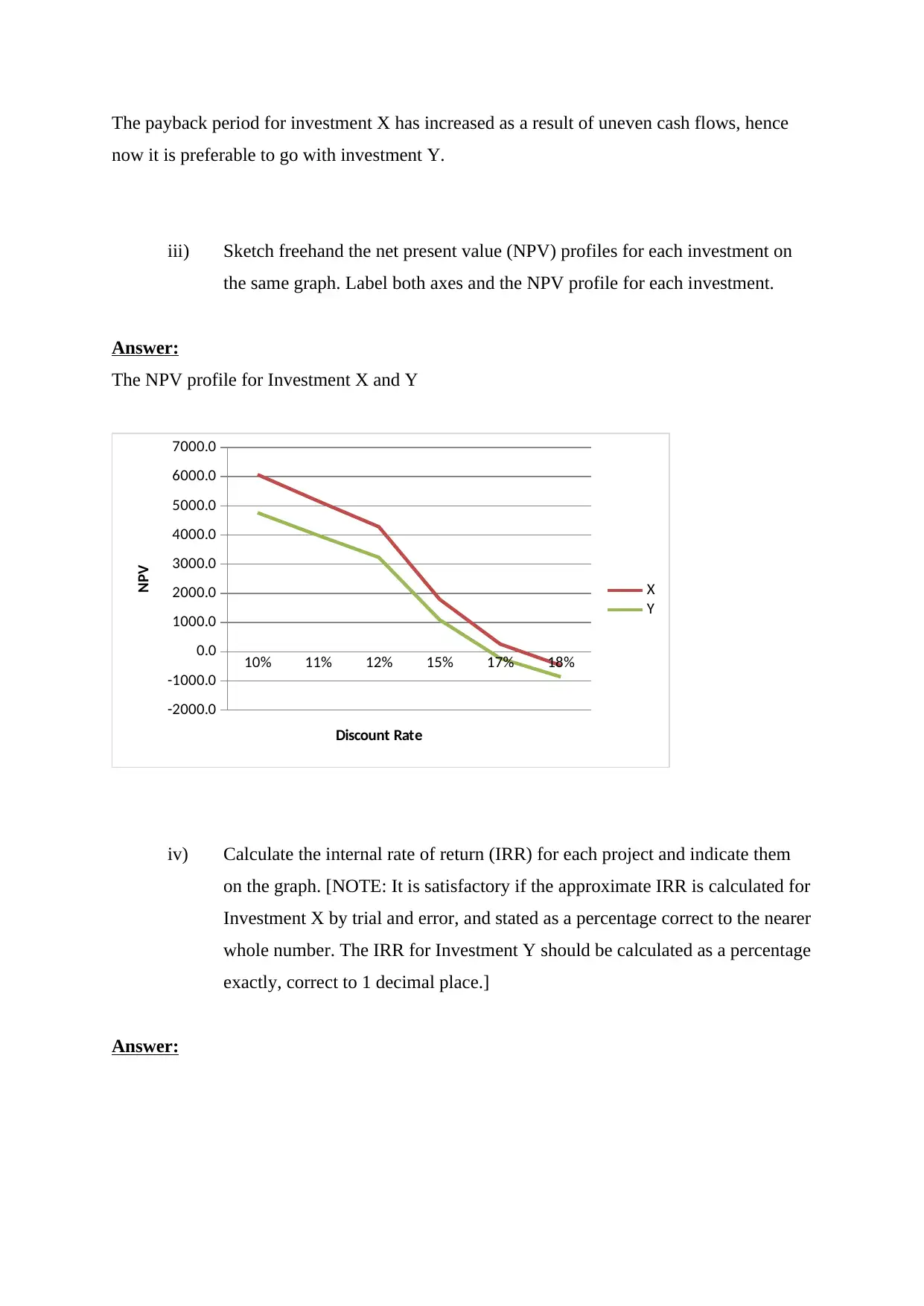
The payback period for investment X has increased as a result of uneven cash flows, hence
now it is preferable to go with investment Y.
iii) Sketch freehand the net present value (NPV) profiles for each investment on
the same graph. Label both axes and the NPV profile for each investment.
Answer:
The NPV profile for Investment X and Y
10% 11% 12% 15% 17% 18%
-2000.0
-1000.0
0.0
1000.0
2000.0
3000.0
4000.0
5000.0
6000.0
7000.0
X
Y
Discount Rate
NPV
iv) Calculate the internal rate of return (IRR) for each project and indicate them
on the graph. [NOTE: It is satisfactory if the approximate IRR is calculated for
Investment X by trial and error, and stated as a percentage correct to the nearer
whole number. The IRR for Investment Y should be calculated as a percentage
exactly, correct to 1 decimal place.]
Answer:
now it is preferable to go with investment Y.
iii) Sketch freehand the net present value (NPV) profiles for each investment on
the same graph. Label both axes and the NPV profile for each investment.
Answer:
The NPV profile for Investment X and Y
10% 11% 12% 15% 17% 18%
-2000.0
-1000.0
0.0
1000.0
2000.0
3000.0
4000.0
5000.0
6000.0
7000.0
X
Y
Discount Rate
NPV
iv) Calculate the internal rate of return (IRR) for each project and indicate them
on the graph. [NOTE: It is satisfactory if the approximate IRR is calculated for
Investment X by trial and error, and stated as a percentage correct to the nearer
whole number. The IRR for Investment Y should be calculated as a percentage
exactly, correct to 1 decimal place.]
Answer:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
10% 11% 12% 15% 17% 18%
-2000.0
-1000.0
0.0
1000.0
2000.0
3000.0
4000.0
5000.0
6000.0
7000.0
X
Y
Discount Rate
NPV
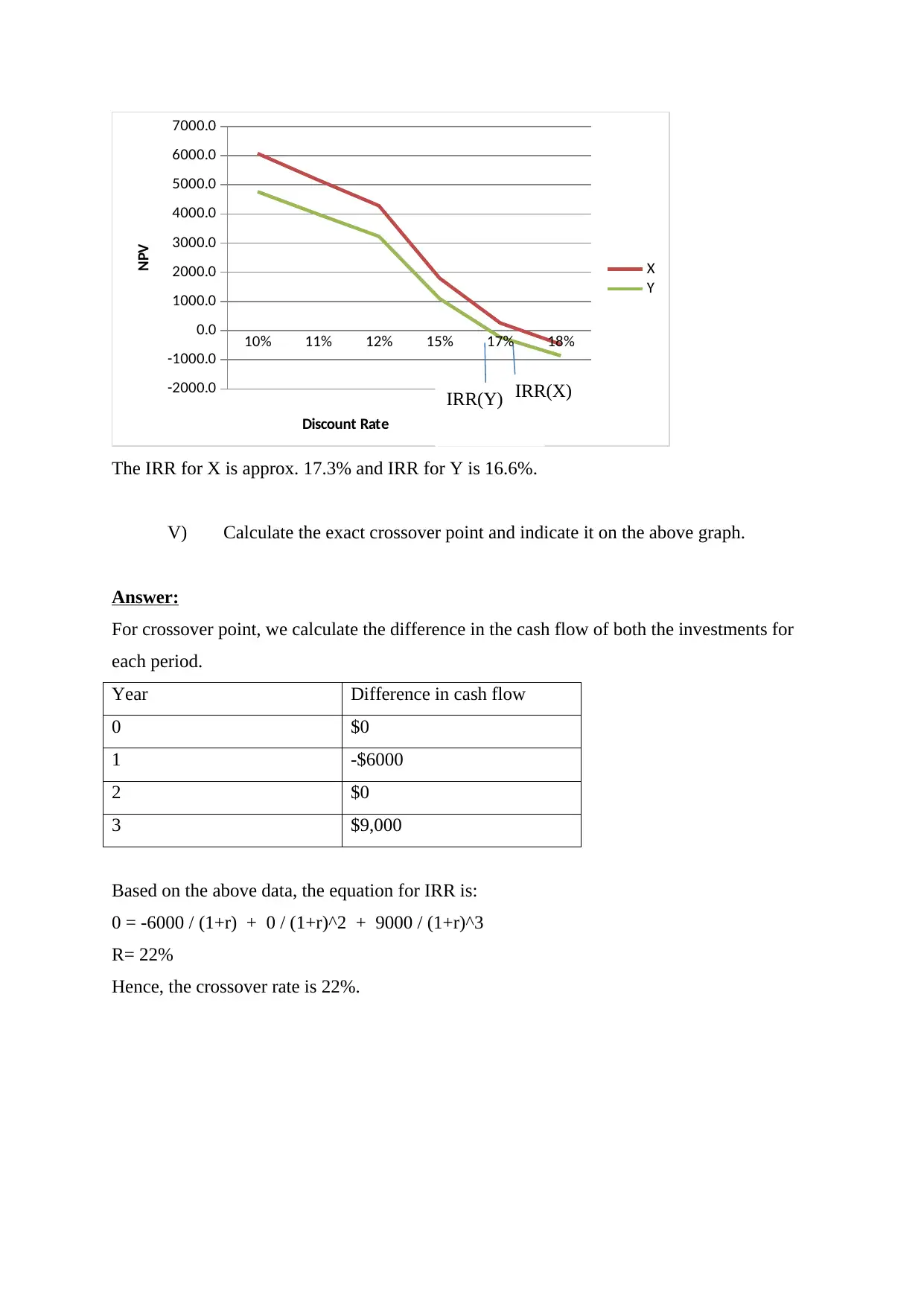
The IRR for X is approx. 17.3% and IRR for Y is 16.6%.
V) Calculate the exact crossover point and indicate it on the above graph.
Answer:
For crossover point, we calculate the difference in the cash flow of both the investments for
each period.
Year Difference in cash flow
0 $0
1 -$6000
2 $0
3 $9,000
Based on the above data, the equation for IRR is:
0 = -6000 / (1+r) + 0 / (1+r)^2 + 9000 / (1+r)^3
R= 22%
Hence, the crossover rate is 22%.
IRR(Y) IRR(X)
-2000.0
-1000.0
0.0
1000.0
2000.0
3000.0
4000.0
5000.0
6000.0
7000.0
X
Y
Discount Rate
NPV
The IRR for X is approx. 17.3% and IRR for Y is 16.6%.
V) Calculate the exact crossover point and indicate it on the above graph.
Answer:
For crossover point, we calculate the difference in the cash flow of both the investments for
each period.
Year Difference in cash flow
0 $0
1 -$6000
2 $0
3 $9,000
Based on the above data, the equation for IRR is:
0 = -6000 / (1+r) + 0 / (1+r)^2 + 9000 / (1+r)^3
R= 22%
Hence, the crossover rate is 22%.
IRR(Y) IRR(X)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
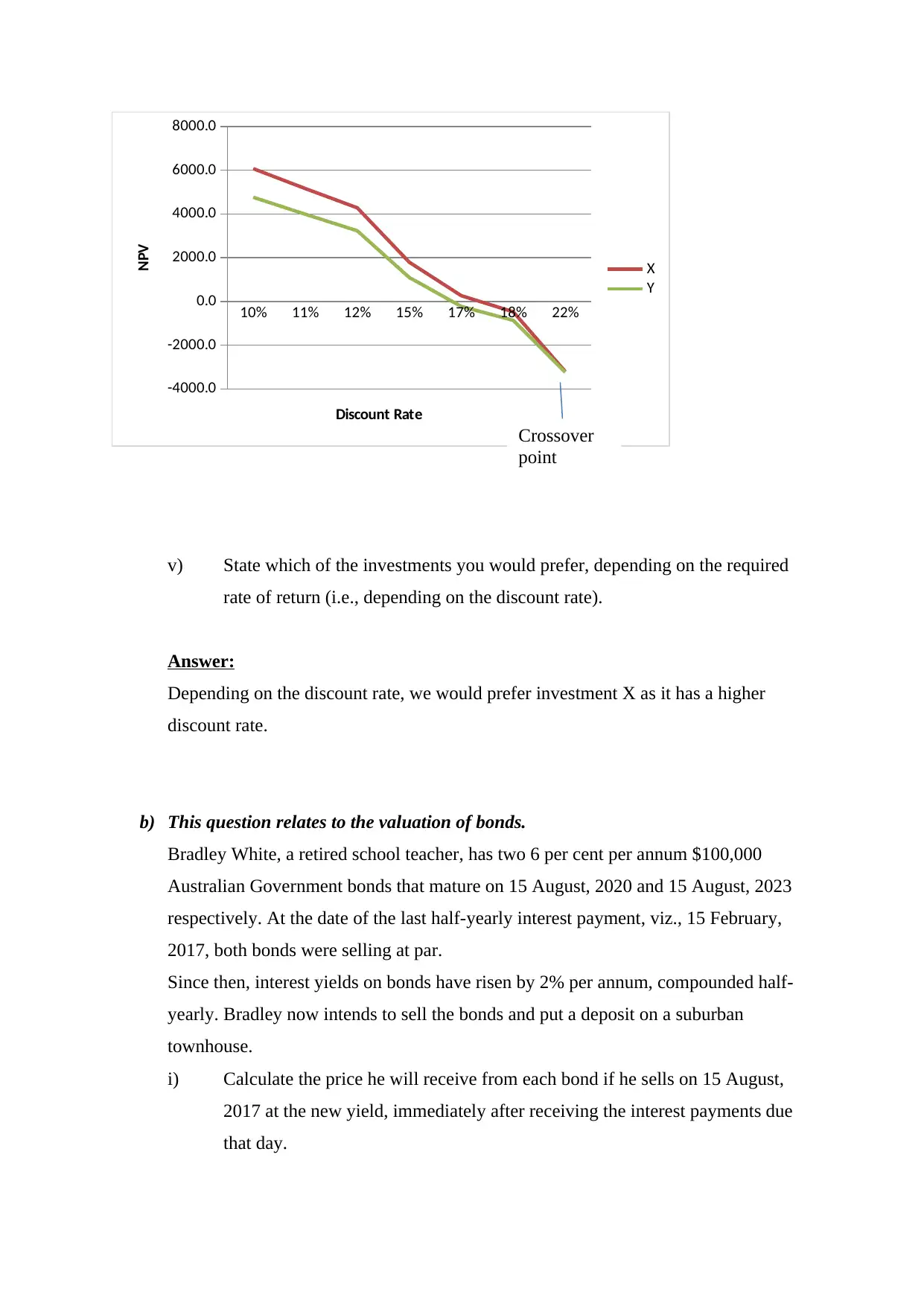
10% 11% 12% 15% 17% 18% 22%
-4000.0
-2000.0
0.0
2000.0
4000.0
6000.0
8000.0
X
Y
Discount Rate
NPV
v) State which of the investments you would prefer, depending on the required
rate of return (i.e., depending on the discount rate).
Answer:
Depending on the discount rate, we would prefer investment X as it has a higher
discount rate.
b) This question relates to the valuation of bonds.
Bradley White, a retired school teacher, has two 6 per cent per annum $100,000
Australian Government bonds that mature on 15 August, 2020 and 15 August, 2023
respectively. At the date of the last half-yearly interest payment, viz., 15 February,
2017, both bonds were selling at par.
Since then, interest yields on bonds have risen by 2% per annum, compounded half-
yearly. Bradley now intends to sell the bonds and put a deposit on a suburban
townhouse.
i) Calculate the price he will receive from each bond if he sells on 15 August,
2017 at the new yield, immediately after receiving the interest payments due
that day.
Crossover
point
-4000.0
-2000.0
0.0
2000.0
4000.0
6000.0
8000.0
X
Y
Discount Rate
NPV
v) State which of the investments you would prefer, depending on the required
rate of return (i.e., depending on the discount rate).
Answer:
Depending on the discount rate, we would prefer investment X as it has a higher
discount rate.
b) This question relates to the valuation of bonds.
Bradley White, a retired school teacher, has two 6 per cent per annum $100,000
Australian Government bonds that mature on 15 August, 2020 and 15 August, 2023
respectively. At the date of the last half-yearly interest payment, viz., 15 February,
2017, both bonds were selling at par.
Since then, interest yields on bonds have risen by 2% per annum, compounded half-
yearly. Bradley now intends to sell the bonds and put a deposit on a suburban
townhouse.
i) Calculate the price he will receive from each bond if he sells on 15 August,
2017 at the new yield, immediately after receiving the interest payments due
that day.
Crossover
point

Answer:
Price of bond = C * F * [(1-(1+r)^-t] / r + F / (1+r)^t
We assume the face value of the bond to be $1000 as it is the standard price of a bond.
Yield on bond expiring in 2020 when selling at par in Feb, 2017:
1000 = 3%*1000 * [(1-(1+r)^-7] / r + 1000 / (1+r)^7
R = 3%
Hence, the semi annual yield on bond is 3%.
Yield on bond expiring in 2023 when selling at par in Feb, 2017:
1000 = 3%*1000 * [(1-(1+r)^-13] / r + 1000 / (1+r)^13
R = 3%
New yield on bond expiring in 2020 = 3% + 3% = 6%
Price of 1st bond = 30 * [(1-(1+0.06)^-7] / 0.06 + 1000 / (1+0.06)^7
= $832.52
New yield on bond expiring in 2023= 3% + 6% = 9%
Price of 2nd bond = 30 * [(1-(1+0.09)^-13] / 0.04 + 1000 / (1+0.09)^13
= $477.16
ii) Explain the relative price movements in the two bonds, as evidenced in your
answer to above.
Answer:
Price of bond = C * F * [(1-(1+r)^-t] / r + F / (1+r)^t
We assume the face value of the bond to be $1000 as it is the standard price of a bond.
Yield on bond expiring in 2020 when selling at par in Feb, 2017:
1000 = 3%*1000 * [(1-(1+r)^-7] / r + 1000 / (1+r)^7
R = 3%
Hence, the semi annual yield on bond is 3%.
Yield on bond expiring in 2023 when selling at par in Feb, 2017:
1000 = 3%*1000 * [(1-(1+r)^-13] / r + 1000 / (1+r)^13
R = 3%
New yield on bond expiring in 2020 = 3% + 3% = 6%
Price of 1st bond = 30 * [(1-(1+0.06)^-7] / 0.06 + 1000 / (1+0.06)^7
= $832.52
New yield on bond expiring in 2023= 3% + 6% = 9%
Price of 2nd bond = 30 * [(1-(1+0.09)^-13] / 0.04 + 1000 / (1+0.09)^13
= $477.16
ii) Explain the relative price movements in the two bonds, as evidenced in your
answer to above.
Answer:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 14
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





