Econometrics: Testing and Analysis

This document provides an introduction to econometrics and discusses various tests and analyses in the field. It covers topics such as testing for autocorrelation, specification errors, heteroscedasticity, and evaluating regression results. The document also provides insights on how to improve regression results through log transformation.

FINANCIAL
ECONOMETRICS

TABLE OF CONTENTS
INTRODUCTION...........................................................................................................................4
QUESTION 1..................................................................................................................................4
1. Testing for autocorrelation by using Durbin-Watson (DW) and Lagrange Multiplier (LM)
tests..............................................................................................................................................5
2. Testing specification errors by using Ramsey Regression Equation Specification Error Test
(RESET)......................................................................................................................................7
3. Test for heteroscedasticity.......................................................................................................8
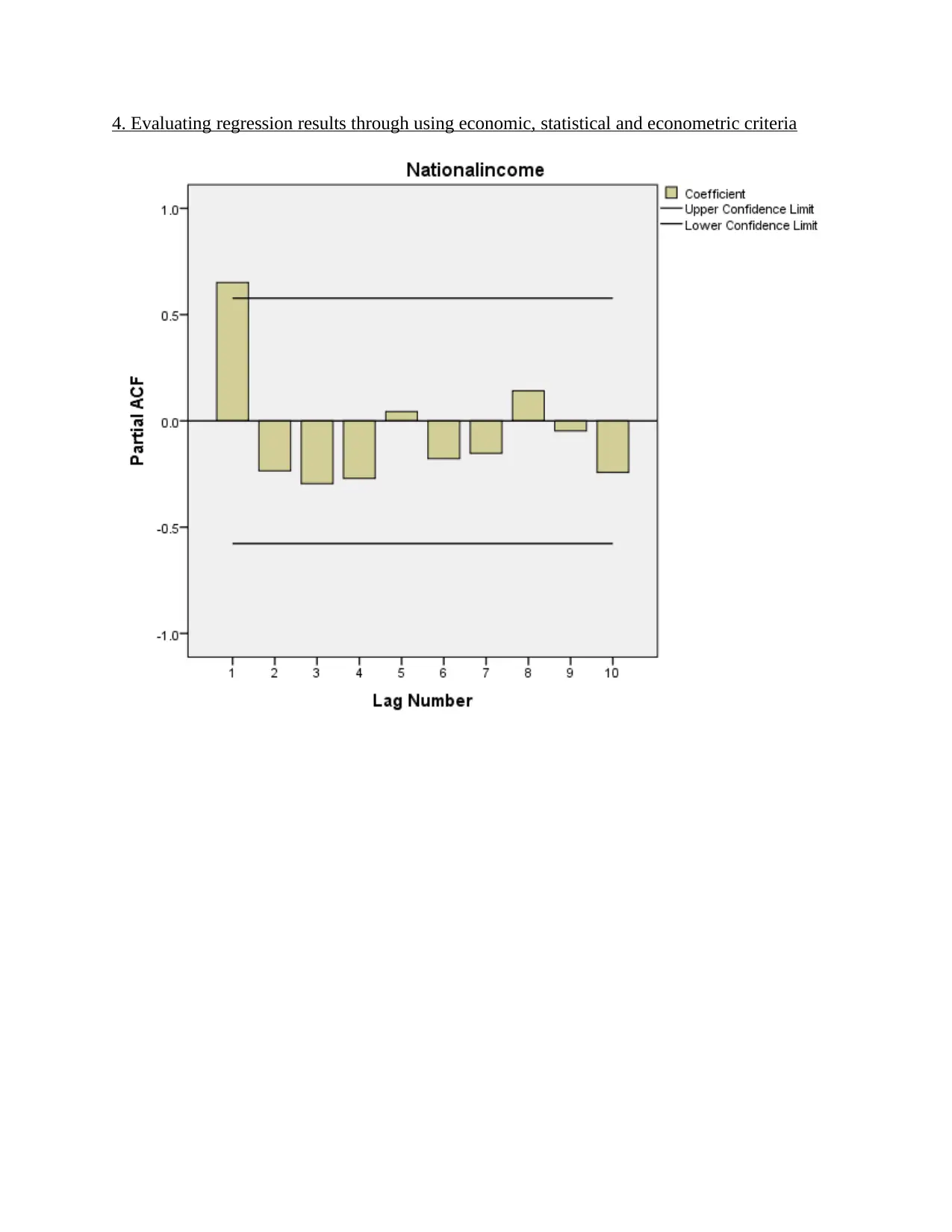
4. Evaluating regression results through using economic, statistical and econometric criteria...9
 10
5. Explaining the manner in which regression results can be improved...................................10
QUESTION 2................................................................................................................................11
Presenting the attractiveness of specific-to-general (S-G) and general-to-specific approaches
related to time series regression models....................................................................................11
QUESTION 3................................................................................................................................11
i. Explaining the difference between the conditional variance and unconditional variance of r
...................................................................................................................................................11
ii. Outlining ARCH and GARCH models that helps in resolving problems.............................12
iii. Assessing the extent to which variance of 𝑒 affects the return on the bond and apply
GARCH model in this regard....................................................................................................12
iv. GARCH model and case.......................................................................................................12
QUESTION 4................................................................................................................................13
(a) Defining below mentioned aspects along with the suitable examples.................................13
i. Covariance Stationary.............................................................................................................13
ii. Trend Stationary....................................................................................................................13

iii. Difference Stationary...........................................................................................................13
(b) Presenting decompositions relevant for trend stationary and stationary processes along
with its usefulness......................................................................................................................14
CONCLUSION..............................................................................................................................14
REFERENCES..............................................................................................................................15
...................................................................................................................................................15

INTRODUCTION
Econometrics implies for the application of statistical and mathematical theories
pertaining to economics. Such tool as well as theoretical framework provides high level of
assistance in testing hypothesis and forecasting future trends. Field of econometrics lays high
level of emphasis on undertaking economic models and testing variables through the means of
statistical trial. Econometrics can be distinguished into two types such as theoretical and applied
which helps analyst in resolving specific issue. The present report will provide deeper insight
about the national income and inflationary trend of Greece. Further, on such data set Durbin-
Watson (DW), Lagrange Multiplier and Ramsey Regression Equation Specification Error Test
(RESET) will be applied to determine suitable outcome. Besides this, report will shed light on the
specific-to-general and general-to-specific approach which is associated with time series regression
model. It will describe the manner S-G and G-S approach helps in dealing with the issue of spurious
regression. Further, it also depicts the extent to which conditional as well as unconditional variances
differ from each other and thereby aid in decision making.
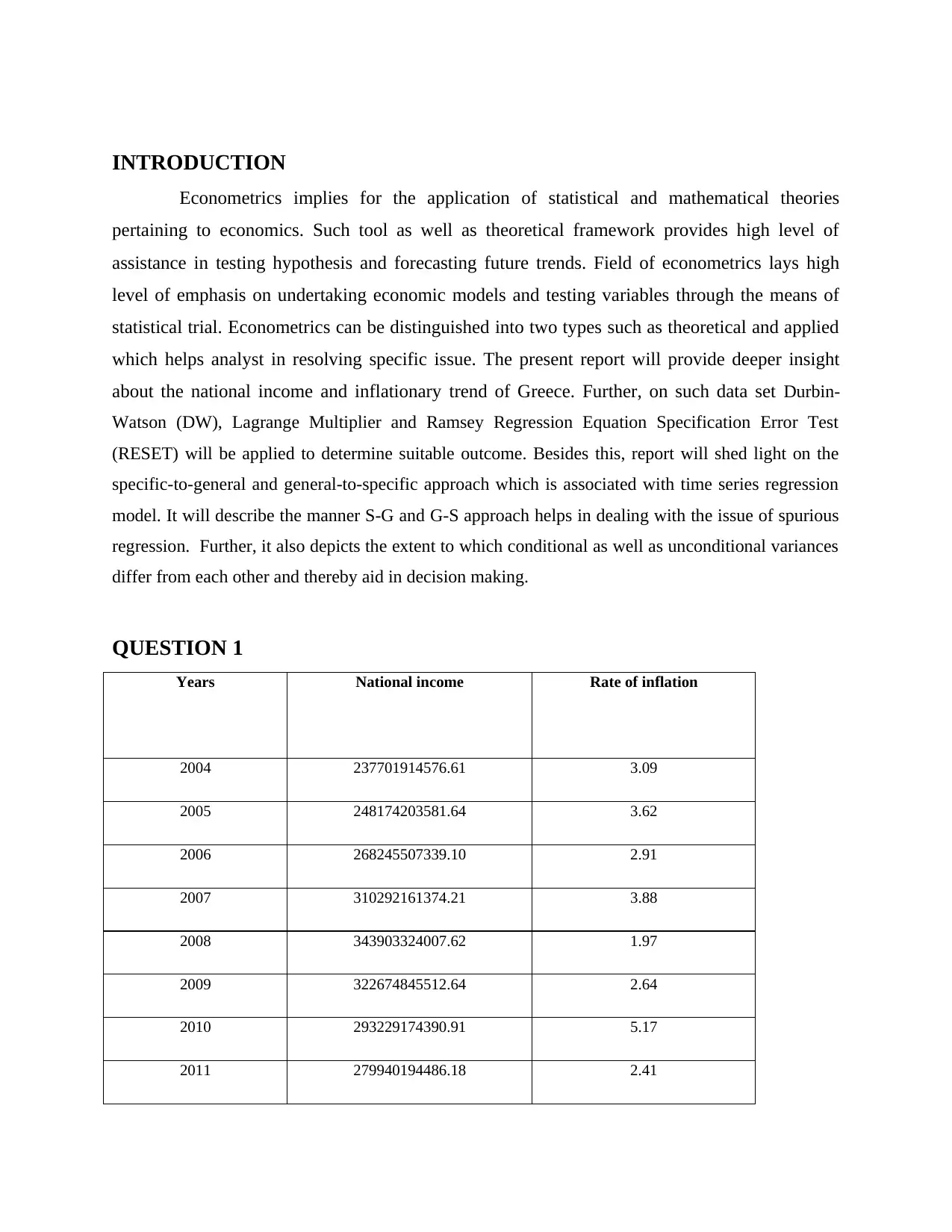
QUESTION 1
Years National income Rate of inflation
2004 237701914576.61 3.09
2005 248174203581.64 3.62
2006 268245507339.10 2.91
2007 310292161374.21 3.88
2008 343903324007.62 1.97
2009 322674845512.64 2.64
2010 293229174390.91 5.17
2011 279940194486.18 2.41

2012 247300884461.34 0.80
2013 239573179546.78 -1.71
2014 236599180334.16 -2.61
2015 195528679024.14 -0.17
2016 195338356749.17 (National income
of Greece, 2017)
0.02 (Inflationary trend of
Greece, 2017)
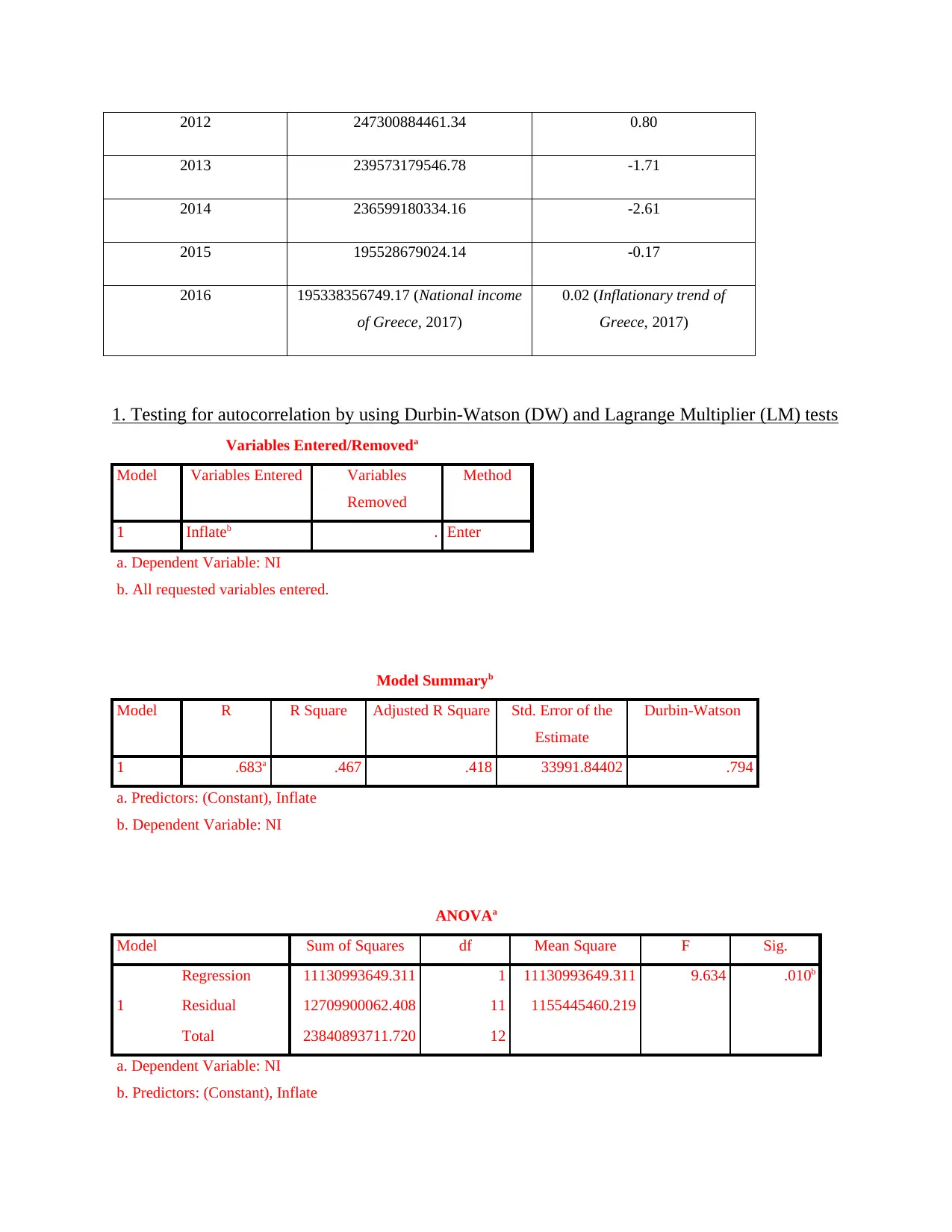
1. Testing for autocorrelation by using Durbin-Watson (DW) and Lagrange Multiplier (LM) tests
Variables Entered/Removeda
Model Variables Entered Variables
Removed
Method
1 Inflateb . Enter
a. Dependent Variable: NI
b. All requested variables entered.
Model Summaryb
Model R R Square Adjusted R Square Std. Error of the
Estimate
Durbin-Watson
1 .683a .467 .418 33991.84402 .794
a. Predictors: (Constant), Inflate
b. Dependent Variable: NI
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1
Regression 11130993649.311 1 11130993649.311 9.634 .010b
Residual 12709900062.408 11 1155445460.219
Total 23840893711.720 12
a. Dependent Variable: NI
b. Predictors: (Constant), Inflate

Coefficientsa
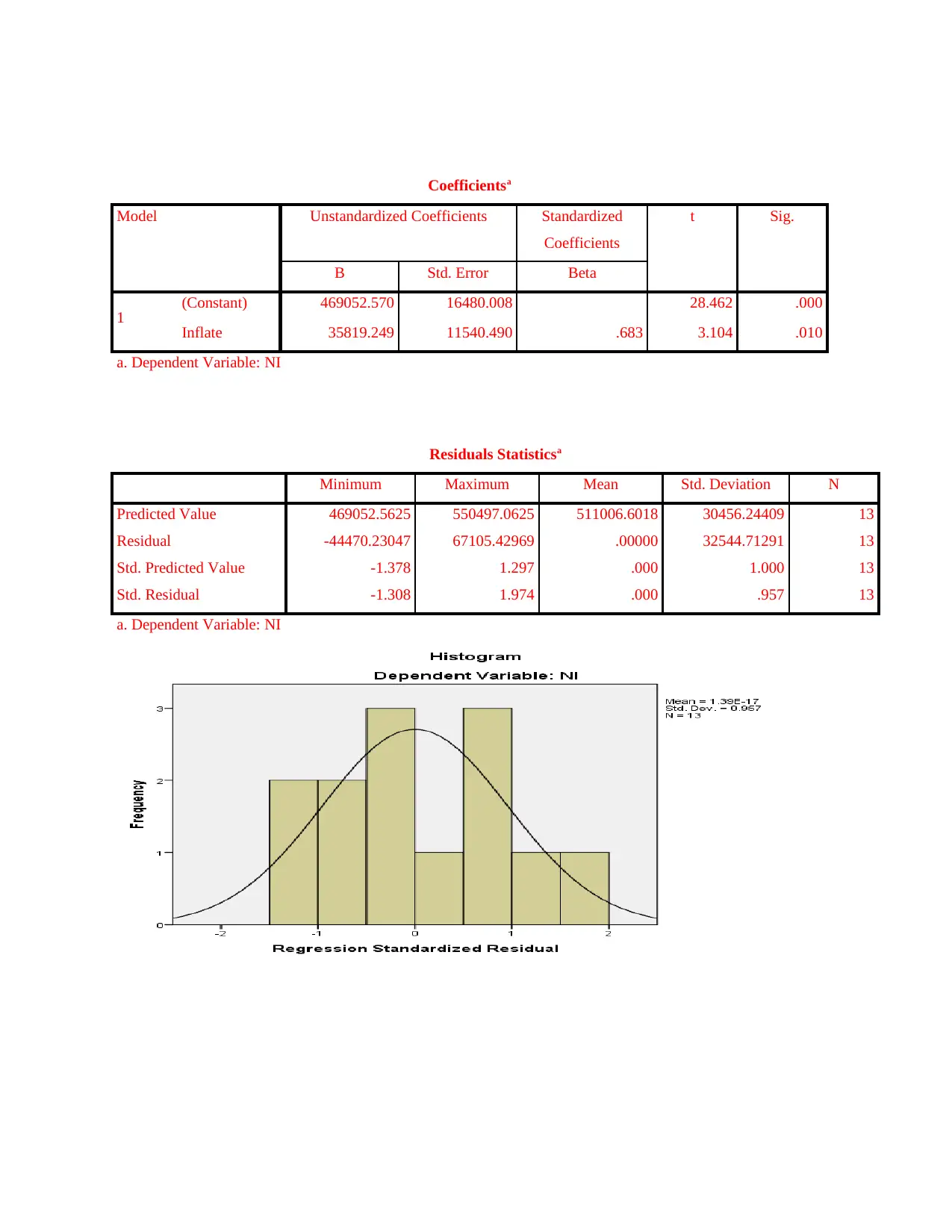
Model Unstandardized Coefficients Standardized
Coefficients
t Sig.
B Std. Error Beta
1 (Constant) 469052.570 16480.008 28.462 .000
Inflate 35819.249 11540.490 .683 3.104 .010
a. Dependent Variable: NI
Residuals Statisticsa
Minimum Maximum Mean Std. Deviation N
Predicted Value 469052.5625 550497.0625 511006.6018 30456.24409 13
Residual -44470.23047 67105.42969 .00000 32544.71291 13
Std. Predicted Value -1.378 1.297 .000 1.000 13
Std. Residual -1.308 1.974 .000 .957 13
a. Dependent Variable: NI

2. Testing specification errors by using Ramsey Regression Equation Specification Error Test
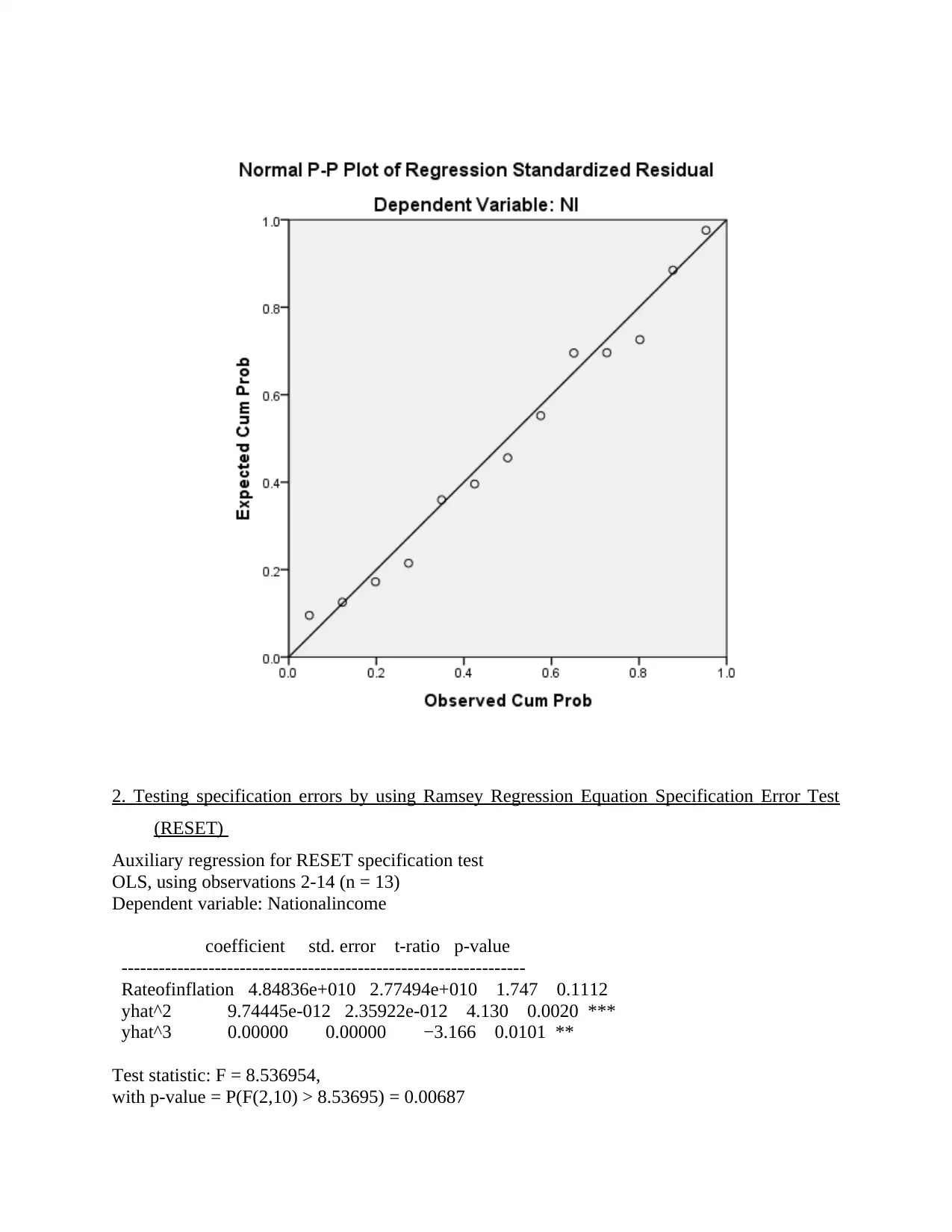
(RESET)
Auxiliary regression for RESET specification test
OLS, using observations 2-14 (n = 13)
Dependent variable: Nationalincome
coefficient std. error t-ratio p-value
-----------------------------------------------------------------
Rateofinflation 4.84836e+010 2.77494e+010 1.747 0.1112
yhat^2 9.74445e-012 2.35922e-012 4.130 0.0020 ***
yhat^3 0.00000 0.00000 −3.166 0.0101 **
Test statistic: F = 8.536954,
with p-value = P(F(2,10) > 8.53695) = 0.00687

Interpretation
RAMSEY test is one that is used to test whether there are some non linear relationship
between variables in the model. In the calculation process polynomials are used in the linear
regression model that is already developed by analyst. RAMSEY is one of the tool that is used
for measuring whether nonlinear combinations of the fitted values help in explaining dependent
variables. Means that in regression model R square tool is commonly used to identify extent to
which independent variables are explaining variation in dependent variable (Draper and Smith,
2014). In case R square value is low it is assumed that less percentage variation in dependent
variable is explained by independent variable which means that there is lack of equality in
variance which is not good for the model. RAMSEY test help data scientist in identifying
whether nonlinear combinations to some extent can explain variance in dependent variable. In
case it is identified that these nonlinear combinations are explaining variance in dependent
variable then it can be said that model to some extent may be effective. Value of level of
significance is 0.00<0.05 which reflect that there are no nonlinear combination in the model and
it is making perfect prediction.
3. Test for heteroscedasticity
White's test for heteroskedasticity
OLS, using observations 2-14 (n = 13)
Dependent variable: uhat^2
coefficient std. error t-ratio p-value
------------------------------------------------------------------
const 5.89987e+022 5.92999e+021 9.949 1.67e-06 ***
Rateofinflation −2.79296e+022 2.64919e+021 −10.54 9.77e-07 ***
sq_Rateofinflati~ 3.52253e+021 8.16543e+020 4.314 0.0015 ***

Unadjusted R-squared = 0.930401
Test statistic: TR^2 = 12.095217,
with p-value = P(Chi-square(2) > 12.095217) = 0.002364
Interpretation
Results are clearly reflecting that there is no presence of heteroscedisty as value of level of
significance is 0.00 which means that there is similarity in variance in residuals across data set.
Procedure that is used for heteroscedisty test is given below.
 Estimate regression mode by taking in to account dependent and independent variables.
 Identify value of R square from auxiliary regression.
 In third stage statistical significance is measured by performing calculated and it is identified
that whether there is homodasticity or heterodasticity in the variable.
 In case computed chi square value is higher then chi value at specific level of significence then
in that case hypothesis of homodasticity is rejected.

4. Evaluating regression results through using economic, statistical and econometric criteria

There are some of the assumptions that need to be fulfilled in order to ensure that reliable
predictions are made under the regression model that is developed for the models.
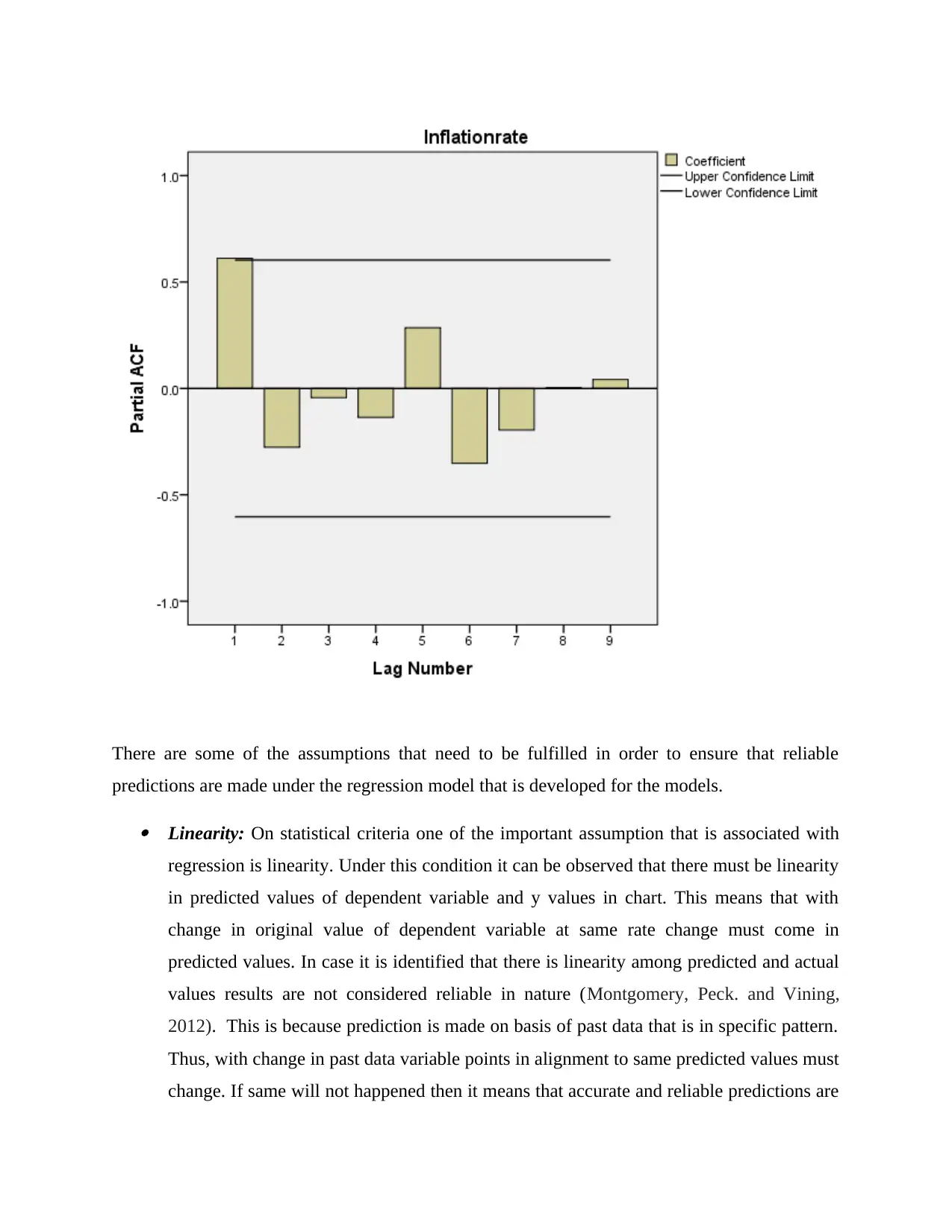
 Linearity: On statistical criteria one of the important assumption that is associated with
regression is linearity. Under this condition it can be observed that there must be linearity
in predicted values of dependent variable and y values in chart. This means that with
change in original value of dependent variable at same rate change must come in
predicted values. In case it is identified that there is linearity among predicted and actual
values results are not considered reliable in nature (Montgomery, Peck. and Vining,
2012). This is because prediction is made on basis of past data that is in specific pattern.
Thus, with change in past data variable points in alignment to same predicted values must
change. If same will not happened then it means that accurate and reliable predictions are

not made which is not good. Hence, linearity is considered as one of the most important
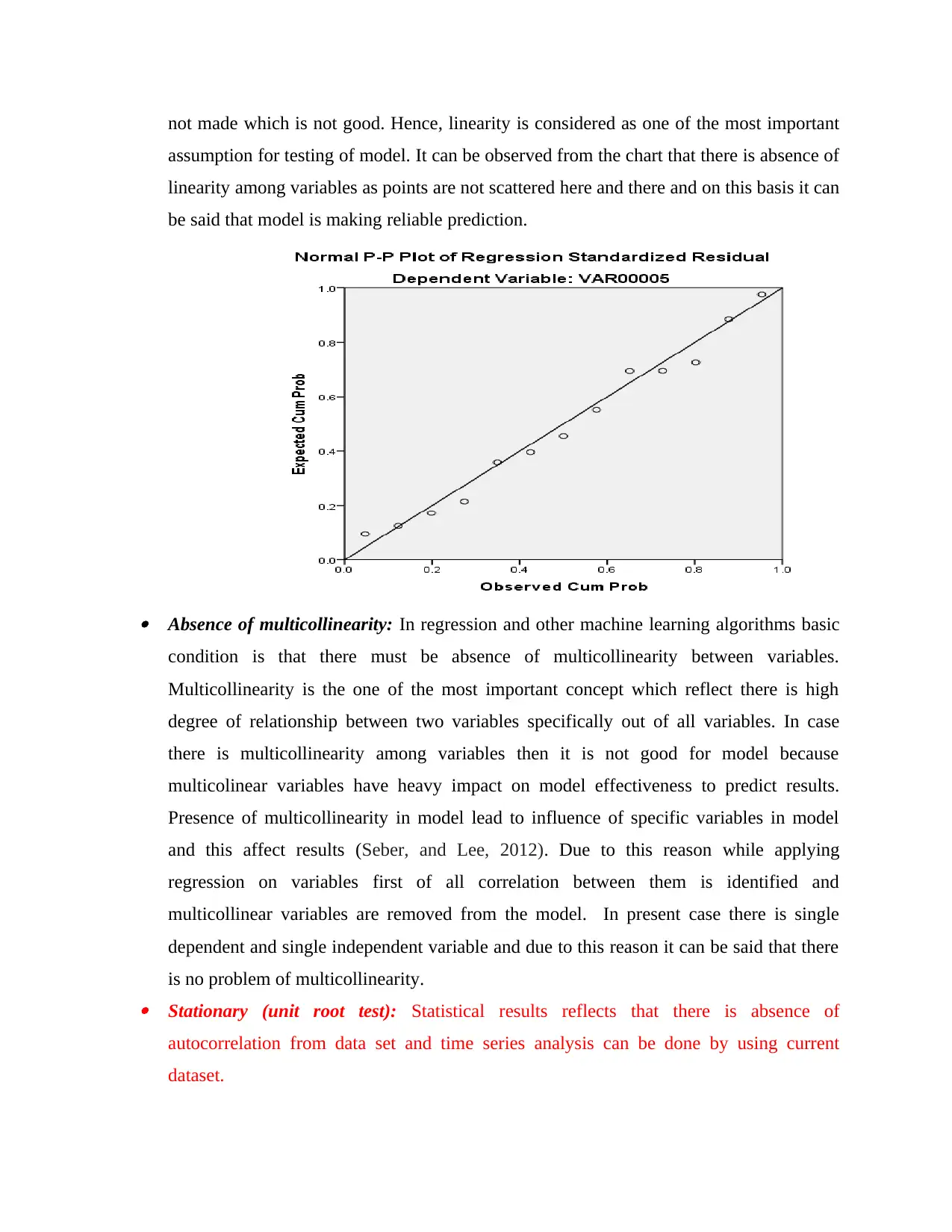
assumption for testing of model. It can be observed from the chart that there is absence of
linearity among variables as points are not scattered here and there and on this basis it can
be said that model is making reliable prediction.
 Absence of multicollinearity: In regression and other machine learning algorithms basic
condition is that there must be absence of multicollinearity between variables.
Multicollinearity is the one of the most important concept which reflect there is high
degree of relationship between two variables specifically out of all variables. In case
there is multicollinearity among variables then it is not good for model because
multicolinear variables have heavy impact on model effectiveness to predict results.
Presence of multicollinearity in model lead to influence of specific variables in model
and this affect results (Seber, and Lee, 2012). Due to this reason while applying
regression on variables first of all correlation between them is identified and
multicollinear variables are removed from the model. In present case there is single
dependent and single independent variable and due to this reason it can be said that there
is no problem of multicollinearity. Stationary (unit root test): Statistical results reflects that there is absence of
autocorrelation from data set and time series analysis can be done by using current
dataset.

 Homoscedasticity or equality in variance in residuals or error terms: Homoscedasticity
is the one of the most important assumption that is associated with regression under which it
is important that variance which is difference between actual and predicted values must be
same. In case there is lack of equality in variance then it can be said that condition is violated
and results fully are not reliable in nature. In present case it can be observed that there is
homoscedasticity because scatter points are scattered here and there in chart. Hence,
condition is fulfilled. Absence of autocorrelation: There must be absence of autocorrelation between residuals
because it is observed that if residuals are inter related to each other than accurate
prediction cannot be made. In other words it can be said that residuals must be
independent from each other. In present case it can be observed that residuals are
arranged in triangular or funnel shape and it can be said that there is lack of absence of
autocorrelation.
5. Explaining the manner in which regression results can be improved
Regression results can be improved and under this there is need to do log transformation
under which dependent and independent variables values will be transformed and linearity will
be bring between dependent and independent variable (Bassler and et.al., 2010). If same will be
done then in that case linearity assumption will be fulfilled which means that in alignment to
change in dependent variable value equal deviation will be observed in predicted values.
Violation of homoscedasticity is another area where there is need to do work as it is observed
many times when regression model is run. In order to solve this problem logarithmic
transformation can be applied to variable that is largely skewed and some of variables can be
transformed using square root. By following these treatments problem of homoscedasticity can
be eliminated (Homoscedasticity, 2017). In order to solve all these problems polynomial
regression can also be used by data scientists. This is because sometimes normally when
regression is run on data set condition does not fulfilled and in such kind of situation it is
polynomial regression that to some extent solve the problem. One of the interesting feature
associated with polynomial regression is that by using same even there is nonlinear relationship
between X and y variable accurate results can be obtained. Hence, even linearity assumption get
violated valid results can be obtained from polynomial regression. There are different degrees of
polynomial regressions and it depend on the analysts that up to what extent it make use of

polynomial regression to solve the problem. Usually, it is observed that high degree of
polynomial are not suitable for analysis purpose because they have their own set of limitations.
QUESTION 2
Presenting the attractiveness of specific-to-general (S-G) and general-to-specific approaches
related to time series regression models
General to specific approach show process that is performed in regression modeling
where at initial stage there are multiple independent variables but only some of them remain in
final model (General-to-specific modeling in Stata, 2014). In this regard, GUM calculation is
performed by using specific algorithm. Hence, those variables that cannot play significant role in
predicting dependent variable are removed from model and in this way mentioned algorithm
assist in solving problem of spurious regression. On other hand, specific to general is traditional
approach where only specific variable are taken at initial stage and if conditions are not fulfilled
then in that case more variables are added to model to fulfill all assumptions (Specific to general
modeling, 2017). In case of this method until it is not identified that model is perfectly making
prediction about dependent variable new variable is added and in this way problem of spurious
regression is solved by using algorithm. In the context of time series regression model, it can be
said that S-G and G-S approaches are highly significant which in turn provides high level of
assistance in dealing with issue of spurious. From assessment, it has been identified that general
to specific modeling technique includes several aspects such as elimination, single and multiple
hypothesis testing, goodness of fit measure and diagnostic tests (General-to-Specific(GETS)
Modelling, 2017). Overview of G-S modeling in terms of linear regression model can be
presented in the following way:
QUESTION 3
i. Explaining the difference between the conditional variance and unconditional variance of r
By doing assessment, it has been identified that significant difference takes place
between conditional and unconditional variance. Hence, unconditional variance may be served as

a standard measure of variance. In contrast to this, conditional variance measures the level of
uncertain pertaining to the variable of specific data set (Covariance stationary process, 2017).
Thus, it can be said that as compared to unconditional, conditional variance provides high level
of assistance in measuring the level of uncertainty.
ii. Outlining ARCH and GARCH models that helps in resolving problems
If error value is deviating at different rate for each observation then in that case standard
ordinary lease square will not be able to accurately estimate parameter value which is beta.
Hence, accurately it will not be possible to identify that what change comes in independent
variable with single change in dependent variable. In accordance with the given situation, if
variances of E changes systematically then in that case ordinary lease square approach will need
to make adjustment in beta values so that sum of square remain less in results. ARCH(1,1) and
GARCH (1,1) model can be used to solve this problem (Bora and et.al., 2011). It depend on
analyst that which of model it find best to solve the problem but given condition will make
model more effective. Hence, it can be said that it is very important to make best choice while
making decisions.
iii. Assessinwith dependent variable to some extent explain varianceg the extent to which
variance of 𝑒 affects the return on the bond and apply GARCH model in this regard
If e affects return on bond then in this regard GARCH (1,1) model is applied on data set.
This model will prove effective because GARCH model is sufficient and it will produce
reliable results. In GARCH model (1,1) acts as parenthesis under which first 1 reflect
number of lag how many autoregressive legs are there are in equation. Whereas, second 1
reflect number of moving aveage lags that are in the model (GARCH 101: An Introduction
to the Use of ARCH/GARCH models in Applied Econometrics, 2017). Many times more
than 1 lag is needed to obtain reliable forecast. Hence, if it estimated that variance of e
effects the return on bond then in that case lag number will enhanced which will bring
stability in variance and in this way GARCH model will be adjusted.
iv. GARCH model and case
Generalized Auto-Regressive Conditional Heteroskedasticity (GARCH) Process mainly
lays emphasis on three steps. In the first stage, analyst makes focus on estimating autoregressive
model that best fitted to the data set. Thereafter, economists lay emphasis on calculating

autocorrelation of the error term in order to identify whether assumption of Heteroskedasticity is
meet up or not and in the last stage hypothesis is testing. GARCH model is highly effectual
which in turn provides assistance to financial professionals in the areas related to trading,
investing etc. Further, GARCH also assists in investigating CAPM model in the best possible
way. Moreover, GARCH model clearly states the manner in which volatility of financial market
can change.
GARCH model or process is autoregressive which highly depends on past squared
observations and variances to assess the current one. Hence, by employing GARCH process
analyst can do modeling of assets return as well as inflationary aspects more effectively and
efficiently. Hence, through employing such process analyst can reduce the level of error and
would become to increase the accuracy of forecasting to a great extent.
QUESTION 4
(a) Defining below mentioned aspects along with the suitable examples
i. Covariance Stationary
Covariance stationary indicate variance of all terms that are in set of values should be
same and variance should not be ascertained on the basis of absolute position. Factor relevant to
distance which is among these variables should be consideration amid to covariance stationary so
that stationary feature can be bring in dataset. From assessment, it has identified that a sequence
of random variables is considered as covariance stationary. Hence, it is when all the terms of
sequence have similar mean and covariance depends on i (difference) rather than n (number).
ii. Trend Stationary
In the context of statistical analysis of time series, stochastic process is recognized as
trend stationary when an underlying tendency can be removed. On the basis of such aspect, in
such stationary trend does not have to be linear. In this, trend of mean or average is deterministic
as compared to others (Trend-Stationary vs. Difference-Stationary Processes, 2017). In
accordance with such aspect, once trend is estimated and removed from the data set the residual
series is known as stationary stochastic process.

yt=μt+εt,
 μt: Deterministic mean trend
 ∑t: stationary stochastic process with mean zero
Hence, such time series decomposition method places high level of emphasis on breaking
down μt into different sources such as secular trend and seasonal component.
iii. Difference Stationary
Difference stationary is one under which difference is computed between data points and
by doing so stationary feature is developed in dataset. In order to make accurate prediction it is
necessary to remove all cyclical and seasonal factors from dataset. Under difference stationary,
means trend is considered as stochastic. Sometimes, aspects of de-trending are not sufficient to
make the series stationary. In this, it is necessary for the analyst to transform the same into a
series of period to period or seasonal differences (Stationarity and differencing, 2017). In other
words, it can be said that when mean, variance and autocorrelation of the series are not constant
on the basis of time then it is recognized as difference stationary.
Such type of stationary can be presented in the following way:
ΔDyt = μ + ψ(L) εt,
(b) Presenting decompositions relevant for trend stationary and stationary processes along with
its usefulness
In case of trend stationary method decomposition can be done by using filters or moving
average and regression method (Trend-Stationary vs. Difference-Stationary Processes, 2017). On
other hand, in case of difference stationary method difference between values is computed and
by following process stationary feature is developed in the model by considering difference
values. Decomposition is the one of the most important process because under this different
trends are removed from data sets. It can be observed that in dataset there may be cyclical,
seasonal and other sort of trends. Presence of these sort of trends in dataset reflect there is huge
fluctuation in datasets. In presence of seasonal, cyclical and other trends it is not possible to
make reliable predictions and in order to solve this problem decomposition process is followed.

Under this, seasonal and cyclical related factor is removed from data set and by doing so
stationary feature is bring in data set and reliable prediction is made. Thus, it can be said that
decomposition is the one of the most important stage of time series analysis.
CONCLUSION
On the basis of above discussion it is concluded that there is significant importance of
statistics for the business firms because by using same prudent decisions can be made by the
managers. In the current report regression analysis is done for relevant variables and it is
identified whether regression model satisfied condition or assumptions of linearity,
multicollinearity and other things. It is also concluded that it is very important to remove
seasonal and cyclical factors from data set because in presence of these factors it is not possible
to make accurate and reliable predictions for the business firms. Hence, it can be said that there
is huge significance of decomposition process for the business firms.

REFERENCES
Books and Journals
Bassler, D. and et.al., 2010. Stopping randomized trials early for benefit and estimation of
treatment effects: systematic review and meta-regression analysis. Jama. 303(12). pp.1180-
1187.
Bora, E. and et.al., 2011. Neuroanatomical abnormalities in schizophrenia: a multimodal
voxelwise meta-analysis and meta-regression analysis. Schizophrenia research. 127(1).
pp.46-57.
Draper, N.R. and Smith, H., 2014. Applied regression analysis. John Wiley & Sons.
Montgomery, D.C., Peck, E.A. and Vining, G.G., 2012. Introduction to linear regression
analysis. John Wiley & Sons.
Seber, G.A. and Lee, A.J., 2012. Linear regression analysis (Vol. 936). John Wiley & Sons.
Online
Covariance stationary process. 2017. [Online]. Available through:
<https://lectures.quantecon.org/jl/arma.html>.
Econometrics, 2017. [PDF]. Available through:<
http://www.stern.nyu.edu/rengle/GARCH101.PDF>.
GARCH 101: An Introduction to the Use of ARCH/GARCH models in Applied
General-to-Specific(GETS) Modelling. 2017. [pdf]. Available through:
<http://www.sucarrat.net/R/gets.pdf>.
Homoscedasticity, 2017. [Online]. Available through:<
http://www.statisticssolutions.com/homoscedasticity/>.
Inflationary trend of Greece. 2017. [Online]. Available through: <
http://www.inflation.eu/inflation-rates/greece/historic-inflation/cpi-inflation-greece.aspx>.

National income of Greece. 2017. [Online]. Available through: <
https://fred.stlouisfed.org/series/MKTGNIGRA646NWDB>.
Stationarity and differencing. 2017. [Online]. Available through:
<https://people.duke.edu/~rnau/411diff.htm>.
Trend-Stationary vs. Difference-Stationary Processes, 2017. [Online]. Available through:<
https://in.mathworks.com/help/econ/trend-stationary-vs-difference-stationary.html?
s_tid=gn_loc_drop>.
General-to-specific modeling in Stata, 2014. [PDF]. Available through:< https://7a4444f1-a-
62cb3a1a-s-sites.googlegroups.com/site/damiancclarke/research/
Clarke_GeneralSpecificStata.pdf?
attachauth=ANoY7crby02AGTpnmqsJZeIyEJhOnc31c3x__QfzpCW4AQd5A-
JP2OcniDgryGBZeg4rhU5kV8AxE4H3QBLx3NLM_mmCzaodo7x-
s1Bg8WM8Nk9gmkmvoh3vcMEYNI3J3HuorrtYOEBHxwBVeDNqbkXtBLJ3LeK-
NEOWLmls9kJbjM_8FzMZrUE2jjaDUmmd9R_K-eT2GuFNWS-
zRhlqfEkaTa8D5J_2e2RygOaTi5D0mHq8-Zzv0Abakj6xRa7HfcpzS-
TWMac2&attredirects=0>.
Specific to general modeling, 2017. [Online]. Available through :<
http://slideplayer.com/slide/5003891/>.