(Solution) Financial Management - Assignment

FINANCIAL MANAGEMENT
STUDENT ID:
[Pick the date]

Question 1
a) Investment today (t=0) is $25,000
Amount received at t=4 is $35,000
Let the annual percentage yield be X %
Then, 25000*(1+(X/100))4 = 35,000
Solving the above, X = 8.78% p.a.
b) The methodology involved takes into consideration the compounding effect since the
interest in every year does not remain same here. Since, every year the amount would
increase by 8.78% , hence interest on the previous interest would also be obtained in this
case. The case where compounding is not considered is the simple interest.
c) Price of shares at t = 0 was $25,000
Dividend income (from t=0 to t=4) = $ 3,000
Selling price of share at t=4 is $ 32,000
Hence, holding period returns = [(32000-25000+3000)/(25000)]*100 = 40%
Question 2
a) The requisite computations are shown below.

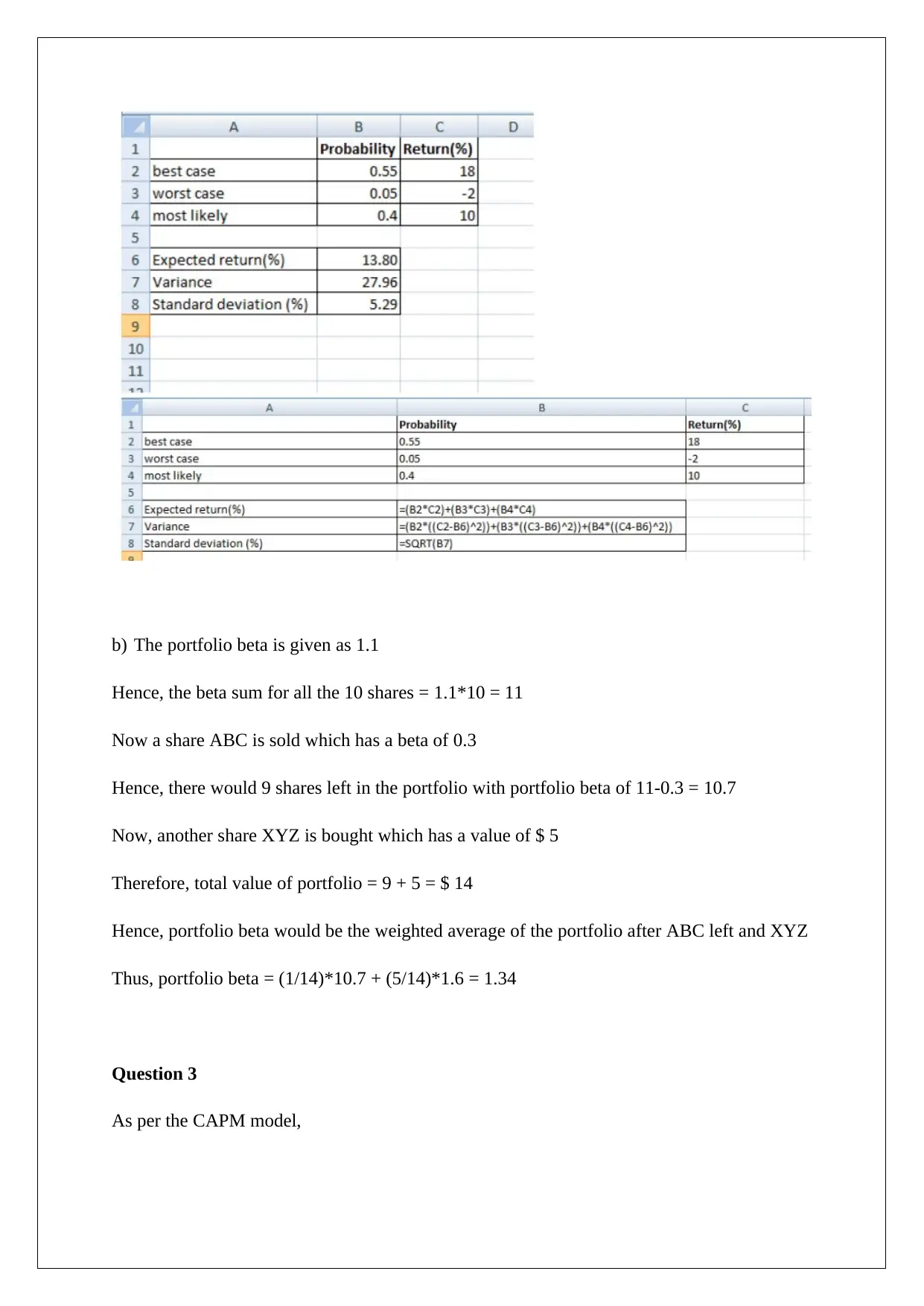
b) The portfolio beta is given as 1.1
Hence, the beta sum for all the 10 shares = 1.1*10 = 11
Now a share ABC is sold which has a beta of 0.3
Hence, there would 9 shares left in the portfolio with portfolio beta of 11-0.3 = 10.7
Now, another share XYZ is bought which has a value of $ 5
Therefore, total value of portfolio = 9 + 5 = $ 14
Hence, portfolio beta would be the weighted average of the portfolio after ABC left and XYZ
Thus, portfolio beta = (1/14)*10.7 + (5/14)*1.6 = 1.34
Question 3
As per the CAPM model,

Expected return on stock = Risk free rate + Beta *(Expected return on market – Risk free
rate)
The given inputs are substituted into the above formula and we get the following.
11.2 = 5.7 + 0.92 (Expected return on market – 5.7)
Hence, (11.2-5.7) = 0.92 (Expected return on market – 5.7)
Solving the above, we get Expected return on market = 11.68% p.a.
Question 4
As per the CAPM model,
Expected return on stock = Risk free rate + Beta *Market Premium
The given inputs are substituted into the above formula and we get the following.
11.8 = 2.5 + Beta * 6.7
Solving the above, we get Beta = 1.39
Question 5
The expected returns need to be computed in accordance with the CAPM approach.
Expected returns on Y Ltd. Shares = 5.2 + 1.6*9 = 19.6% p.a.
Expected returns on Z Ltd. Shares = 5.2 + 1.03*9 = 14.47% p.a.
The returns delivered on Y Ltd shares at 16.2% are less than the computed 19.6%. Hence,
this share is inaccurately priced and is overvalued.
The returns delivered on Z Ltd shares at 15.73% are more than the computed 14.47%. Hence,
this share is inaccurately priced and is undervalued.
Question 6

Face value = $ 500,000
Current yield = 3% p.a.
Time to maturity = 100 days
The relevant computation can be proceeded in the following manner.
3% = [(F-P)/P]*(365/100)
0.03= [(500000-P)/P]*(365/100)
Solving the above, we get P = $495,923.91
Question 7
The relevant computation can be proceeded in the following manner.
2.65% = [(F-P)/P]*(365/60)
Hence, 0.0265 = [(500000-P)/P]*6.083
Solving the above, we get P = $497,831.36
Question 8
Time to maturity = 20 years or 40 half years
Face value of bonds = $ 1,000
Coupon rate offered = 8% p.a.
Coupon payments are semi-annual with $ 40 each.
Effective annual rate of interest = 7.25%
Let the YTM currently be x% per annum
Hence, (1+(X/200))2 = 1.0725
Therefore, X = 7.12% p.a.

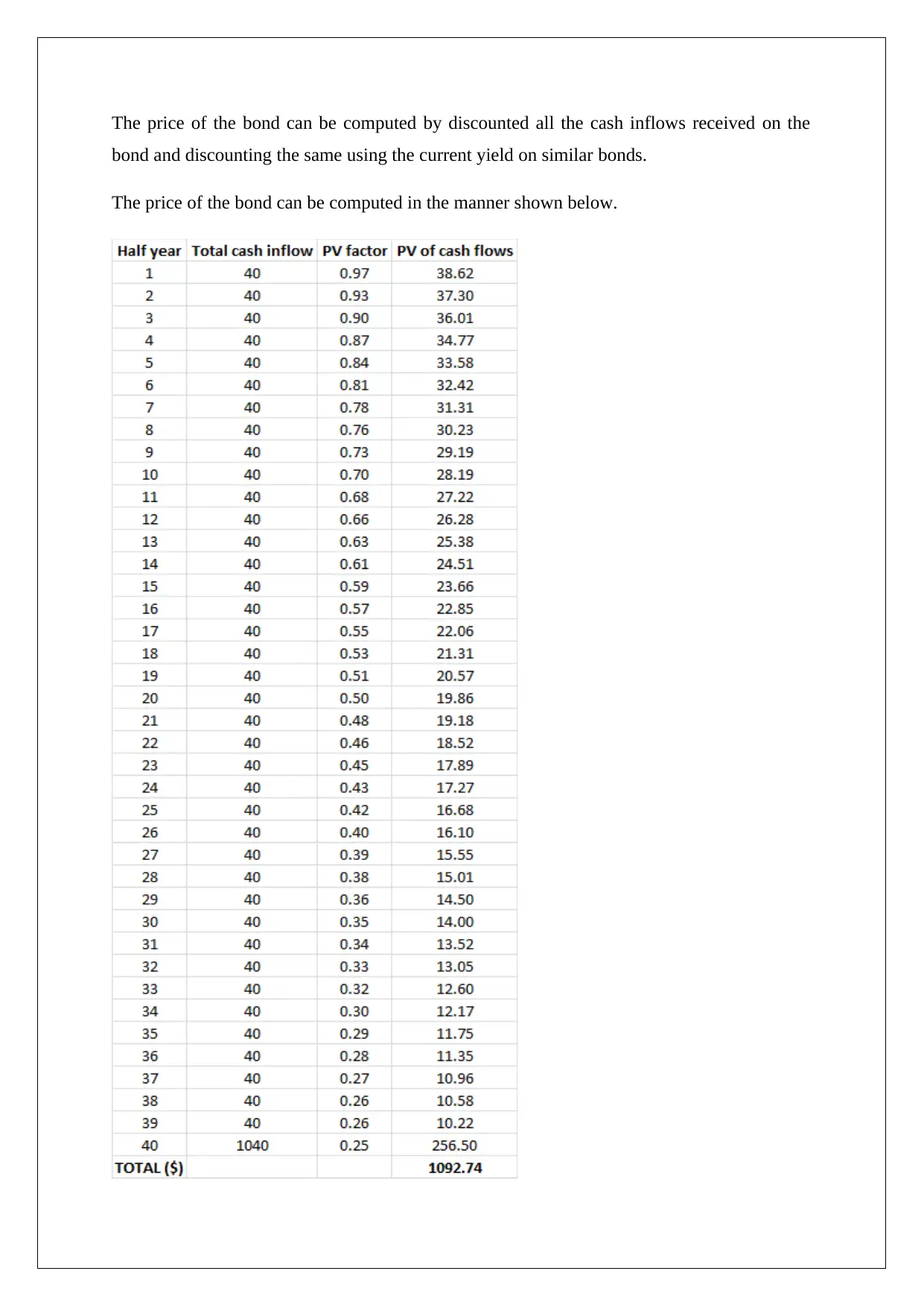
The price of the bond can be computed by discounted all the cash inflows received on the
bond and discounting the same using the current yield on similar bonds.
The price of the bond can be computed in the manner shown below.

From the above computation, the price of the bond is $ 1,092.74.
Question 9
a) Since the bond price would be equal to the $ 1000 or the face value, hence this implies that
the nominal interest and coupon rate would be the same. Thus, the nominal interest rate on
the bond would be 8% p.a.
b) Since the coupon payment would be paid semi-annually, hence the effective rate of
interest would be higher than the nominal rate of 8% p.a.
Effective rate of interest (EAR) = (1+ (8/200)2 -1 = 8.16%
Hence, EAR in the given case is 8.16%.
Question 10
a) The relevant formula is as shown below.
Price = D1/(k-g)
In the given case, price = $ 53, D1 = 3*1.05 = $3.15 , g= 5% or 0.05
Hence, 53 = 3.15/(k-0.05)
Solving the above, k = 10.94% p.a.
b) It is now given that k = 6.75%
Hence, price = 3.15/(0.0675-0.05)
Solving the above, we get price = $ 180

Question 11
a) The required rate of return can be computed using the CAPM approach.
Hence, required rate of return = Risk free rate + Beta * Market Premium
Risk free rate = 2.5%, Beta of CBA stock = 1.2, Market Premium = 6% p.a.
Therefore, required rate of return = 2.5 + 1.2*6 = 9.7% p.a.
b) Since the dividend payout ratio would remain the same, hence the earnings growth rate
would be equal to the dividend growth rate.
Intrinsic share price = D1/(k-g)
k = 9.7% , g = 3%, D1 = 0.7*7.5*1,03 = $ 5.4075
Thus, fair price of a CBA share = 5.4075/(0.097-0.03) = $80.71
The current market value of CBA share is 75. It is apparent that the share is below the
intrinsic price of $ 80.71 and hence undervalued at current price. Thus, CBA shares should be
bought at the current price.
Question 12
a) The average returns can be computed by adding the returns over the five year period and
dividing the same by 5.
Hence, average returns = (16+12-28-7+29)/5 = 4.4% p.a.
b) The variance on the returns is computed using the following table.

Variance = 0.19772/(5-1) = 0.04943 or 4.94%
Standard deviation = √Variance = √(0.04943) = 0.2223 or 22.23%
Question 13
a) Owing to inflation being 1.2%, the nominal returns for each year would be reduced by the
amount of inflation or 1.2%.
Hence, average real return = Average nominal return – Inflation rate = 4.4% -1.2% = 3.2%
b) Further, nominal risk premium = Nominal return – Cash rate = 4.4% - 2.1% = 2.3%
Question 14
The average real risk free rate is equal to cash rate minus the inflation which is equal to (2.1-
1.2) = 0.9% p.a.
Average real risk premium is equal to the nominal real risk premium minus the inflation
which is equal to (2.3% -1.2%) = 1.1%.