FDM Analysis of 2D Heat Transfer: A Solid Body Application
VerifiedAdded on 2023/06/07
|8
|1673
|248
Report
AI Summary
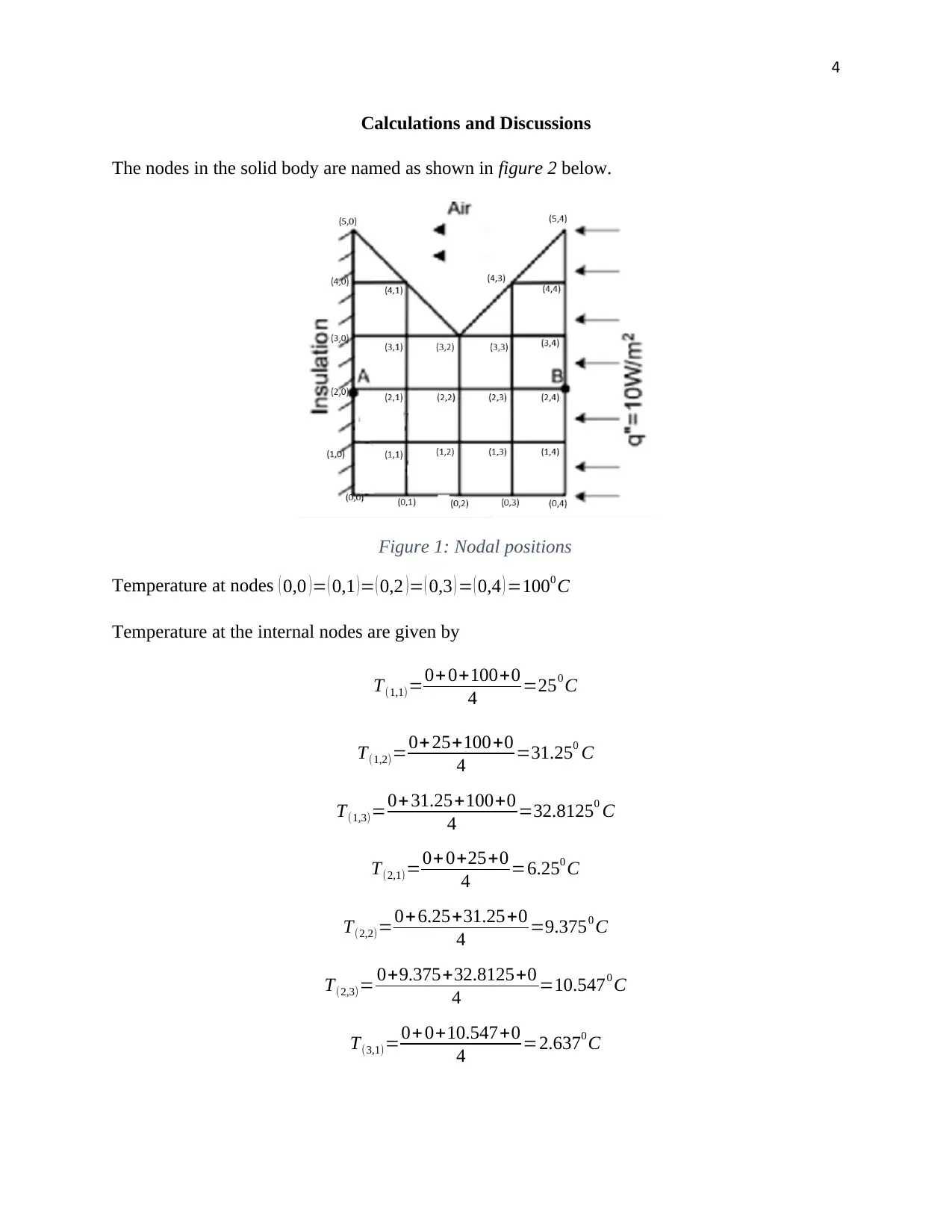
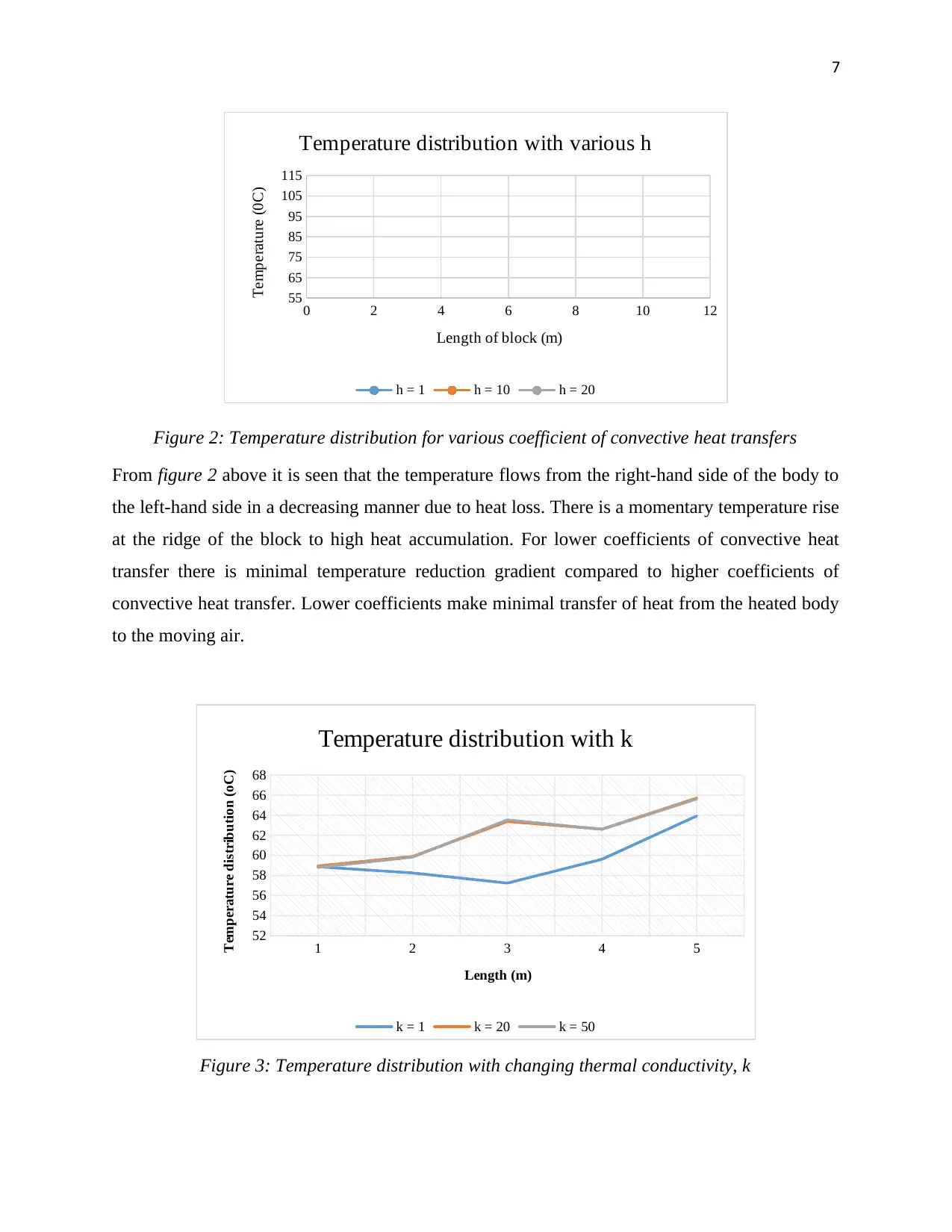
This report provides a detailed analysis of steady two-dimensional heat transfer in a solid body using the Finite Difference Method (FDM). The report begins with an introduction to heat transfer, defining it as energy in transit due to temperature differences and discussing the modes of conduction, convection, and radiation. The core of the report involves applying FDM to determine temperature distributions within a solid body with specific boundary conditions: a maintained bottom surface temperature, a convective top surface, an insulated left side, and a right side subjected to constant heat flux. The calculations section details the determination of nodal temperatures using iterative methods in an Excel workbook, considering heat flux, insulated boundaries, and convective heat transfer. The results are presented in tables and graphs, illustrating temperature distributions for varying convection coefficients (h) and thermal conductivities (k). The analysis concludes that temperature decreases from right to left due to heat loss, with variations based on convective heat transfer coefficients and thermal conductivity values. The findings are relevant to the design of electronic gadgets and PCBs, allowing designers to simulate heat distribution and identify components vulnerable to heat effects. The report references several key texts on heat transfer and numerical methods.
1 out of 8













![[object Object]](/_next/static/media/star-bottom.7253800d.svg)