Flight of a Golf Ball

This document discusses the flight of a golf ball and its motion characteristics. It covers topics such as projectile motion, analyzing motion in a fluid, developing a model for the motion, and limitations of the model. The document also includes references for further reading.

Running head: FLIGHT OF A GOLF BALL 1
Flight of a golf ball
Firstname Lastname
Kenmore State High School

FLIGHT OF A GOLF BALL 2
Question 1
a)
Taking y (t ) as the displacement of the particle at time t; velocity v= dy
dt = ˙y
dy
dt = δy
δt = ˙y ………………………. (i)
δy= ˙y δt ……………………...(ii) provided δt is small.
But δy= y1− y0, substituting in (ii) we get;
y1− y2= ˙y δt
Similarly, at time tn;
yn− yn−1 = ˙yn−1 δt
Rearranging, we obtain;
yn= ˙yn−1 δt + yn−1
b)
i)
From [A], xn−xn−1= ˙xn−1 δt
Rearranging, we get;
xn= ˙xn−1 δt+ xn −1
Differentiating both sides with respect to x, we obtain;
˙xn= ¨xn−1 δt+ ˙xn −1
In simple terms vf =at +vi
ii)
From part (a); yn= ˙yn−1 δt + yn−1
Differentiating both sides with respect to y, we obtain;

FLIGHT OF A GOLF BALL 3
˙yn= ¨yn−1 δt + ˙yn−1
c)
Initial velocity ¿ v m/s
Angle of elevation ¿ θ degrees
Initial velocity on horizontal component vx=v cos θ
Thus, ˙x0=v cos θ
Initial velocity on vertical component v y=v sin θ
Hence, ˙y0=v sinθ
Acceleration along the y-axis is equal to the gravitational acceleration.
¨y0=g
Horizontal component of the acceleration is obtained as follows;
˙x1= ¨xn−1 δt + ˙xn−1
Substituting known values and making ¨xn−1 the subject;
¨xn−1= ˙x1−v cos θ
δt
Question 2
x(t) y(t) xdot(t) ydot(t)
xDDot(t
) yDDot (t)
0 0
60.621
8 35 -18.1865 -20.31
6.0622 3.5000
58.803
1 32.969 -17.6409 -19.7007

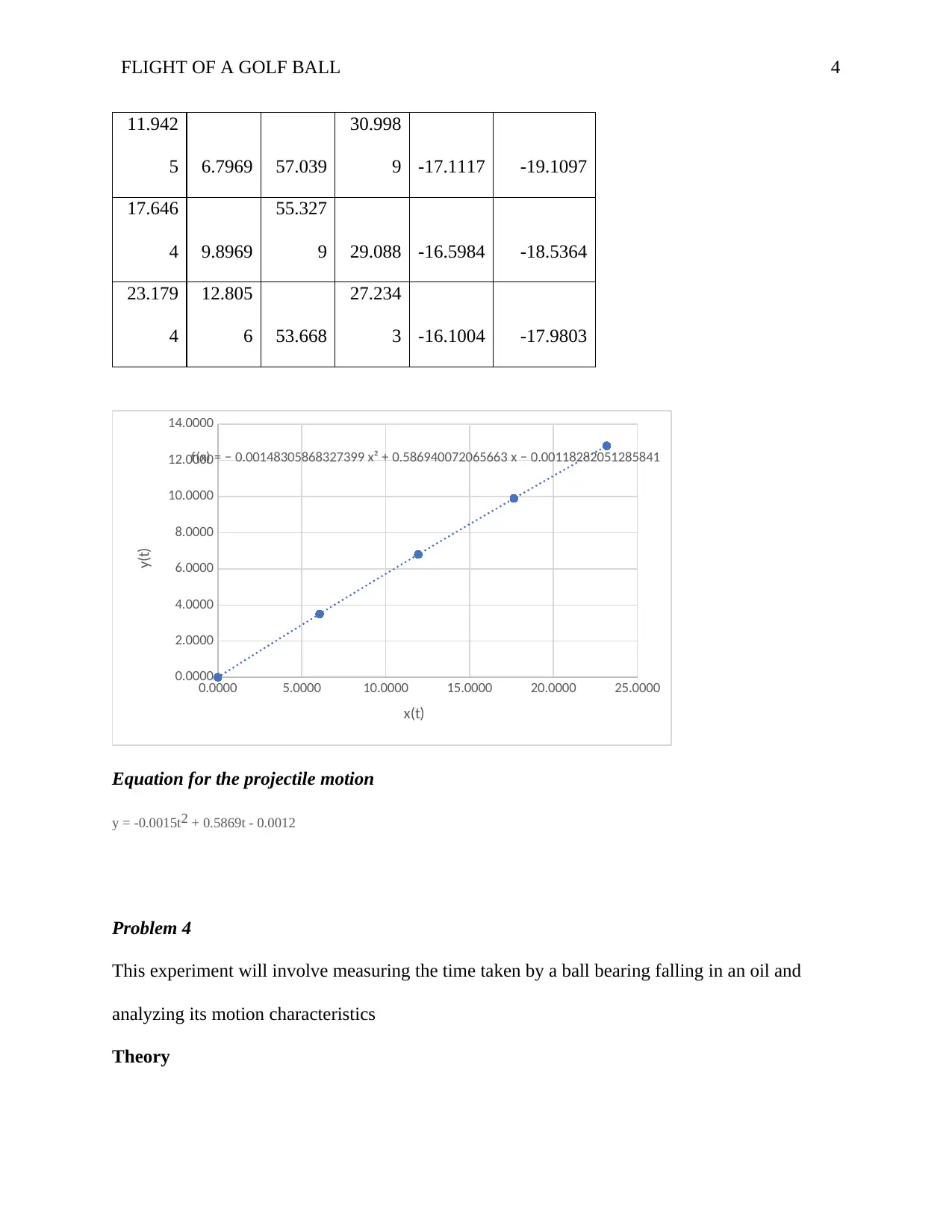
FLIGHT OF A GOLF BALL 4
11.942
5 6.7969 57.039
30.998
9 -17.1117 -19.1097
17.646
4 9.8969
55.327
9 29.088 -16.5984 -18.5364
23.179
4
12.805
6 53.668
27.234
3 -16.1004 -17.9803
0.0000 5.0000 10.0000 15.0000 20.0000 25.0000
0.0000
2.0000
4.0000
6.0000
8.0000
10.0000
12.0000
14.0000
f(x) = − 0.00148305868327399 x² + 0.586940072065663 x − 0.00118282051285841
x(t)
y(t)
Equation for the projectile motion
y = -0.0015t2 + 0.5869t - 0.0012
Problem 4
This experiment will involve measuring the time taken by a ball bearing falling in an oil and
analyzing its motion characteristics
Theory

FLIGHT OF A GOLF BALL 5
A graph having displacement on y-axis and time on x-axis is used to analyzed the motion of an
object falling in a fluid.
A straight-line graph indicates that the object is travelling at a constant velocity, the steeper the
slope of the line indicates that the velocity of the falling object is high. The slope or the gradient
of the line is always the velocity of the falling object in a fluid.
A falling object through air or liquid is opposed by a viscous force. The resisting force increases
with increase in velocity. At the point when the resistive force is the same as gravitational force,
the resultant forces becomes zero and the falling object attains zero acceleration, the velocity
becomes constant hence termed as terminal velocity.
The experiment involves getting time and recording time that the ball bearing takes to fall down
the oil. The terminal velocity is also a key factor.
Steps
1. the measuring cylinder is filled with oil (fluid)
2. 10 distance markers are decided on on the sides of the cylinder
3. Time is placed ready and the bearing is dropped into the fluid.
4. Time is recorded when the ball reaches the marked distance
5. The ball bearing is removed from the cylinder
6. The experiment is repeated and average time computed
Result and data representation
The result is recorded in table form having displacement, which is the distance from oil surface
and time taken by the ball to fall. The displacement is in meters with time in seconds
A graph of displacement on y-axis versus time on x-axis was plotted

FLIGHT OF A GOLF BALL 6
Problem 5: Developing a model
Model FR =−∝ v2 ma=mg−∝ v2
The approach FR =−∝ v2 ma=mg−∝ v2
For the object falling from rest through fluid the forces experience comprise are the gravitational
force FG (weight) and the resistive force FR.
We assume that the direction of motion is on positive direction
The model is derived from Newton’s Second Law
ma=m dv
dt =FG−FR=mg−α v2
( v
|v|)a=g− α
m v2 ( v /|v|)
The acceleration of the object is represented by a.
We take the condition as t ¿ 0 v=v0 x=0 a=g− ( α /m ) v0
2
( v0
|v0| )
For acceleration, a = 0, the velocity is constant v = vT where vT is the terminal velocity
0=mg−α vT
2 vT
2= mg
α
vT = √ mg
α
The model is derived from the equation of motion later integrated with the limits having initial
conditions of t = 0 and v = v0 with final conditions t and v.
The equation depends on v2, the separate analytical calculations for falling motion

FLIGHT OF A GOLF BALL 7
The falling object always have positive value v0 ≥ 0 v ≥ 0
Equation of motion
a=g− α
m v2
a= dv
dt =g− ( α
m ) v2
dt= dv
g− ( α
m ) v2
= dv
( α
m ) (( mg
α ) −v2
) vT
2= mg
α
−( α
m ) dt= dv
v2−vT
2 = ( 1
2 vT )( 1
v −vT
− 1
v+ vT ) dv −( 2 √ mg
α ) ( α
m ) dt =
( 1
v −vT
− 1
v+ vT ) dv
− √ 4 αg
m dt= ( 1
v −vT
− 1
v+vT )dv− √ 4 αg
m ∫
0
t
dt=∫
v0
v
( 1
v−vT
− 1
v + vT )dv
− √ 4 αg
m t = [ −loge ( v−vT ) −loge ( v + vT ) ] v0
v
√ 4 αg
m t= [ loge ( v−vT ) +loge ( v+ vT ) ]v0
v
√ 4 αg
m t= [loge ( v−vT
v0−vT )+loge ( v −vT
v0−vT ) ]
− √ 4 αg
m t =loge {( v−vT
v0 −vT )( v0 + vT
v+ vT ) } ( v−vT
v0 −vT )( v0 + vT
v+vT )=e− √ 4 αg
m t
√ 4 αg
m = √ 4 α g2
mg =
√ 4 g2
vT
2 = 2 g
vT
v−vT = ( v+vT ) ( v0−vT
v0 + vT )e
−2 g
vT
t
= ( v+ vT ) K K= ( v0 −vT
v 0+ vT )e
−2 g
vT
t
v ( 1−K ) =vT ( 1+ K ) v=vT ( 1+ K
1−K )
v=vT
( 1+ ( v0 −vT
v0+vT )e
−2 g
vT
t
1−
( v0−vT
v0 +vT )e
−2 g
vT
t
) v=vT
( ( v0 +vT ) + ( v0−vT ) e
−2 g
vT
t
( v0 + vT ) − ( v0 −vT ) e
−2 g
vT
t )
Applicable on when v0 ≥ 0 v ≥ 0

FLIGHT OF A GOLF BALL 8
The displacement x as a function of velocity v is computed as follows
a= dv
dt = vdv
dx =g− ( α
m )v2 vdv
dx = ( α
m )( mg
α −v2
)vT
2=mg/α
dx= ( m
α ) vdv
( vT
2−v2 ) = (−V T
2
2 g ) (−2 v ) dv
( vT
2−v2 ) ∫
0
x
dx=( −vT
2
2 g )∫
v0
v ( −2 v )
( vT
2 −v2 ) dv x= ( −vT
2
2 g ) [ loge ( vT
2−v2 ) ] v0
v
x= ( vT
2
2 g )loge ( vT
2−v0
2
vT
2−v2 )
valid only if v0 ≥ 0 v ≥ 0
as time tends towards infinite, time t → ∞ we have
v ( t → ∞ ) =vT ( ( v0 +vT ) +0
( v0+ vT )−0 ) e
−2 g
vT
t
→ 0 v ( t → ∞ ) =vT
When object falls the constant velocity will be realized thus v T (a=0) , this also equal to
terminal velocity
t → ∞ v → vT vT −v → 0 1
vT −v → ∞x= (V T
2
2 g )loge ( vT
2−v0
2
vT
2−v2 )→ ∞
Another assumption for this model is that time t for falling object increases with increase in
displacement.
Limitations for the model
The model is limited to the mass of the object falling in the fluid, the applied force during
releasing from the resting station and the velocity of the object
Conclusion

FLIGHT OF A GOLF BALL 9
It can be concluded that an object falling from rest through fluid the forces experience includes
the gravitational force FG (weight) and the resistive force FR which are directly proportional

FLIGHT OF A GOLF BALL
10
References
Hayen, J. C. (2013). Projectile motion in a resistant medium Part II: approximate solution and
estimates. International journal of non-linear mechanics, 38(3), 371-380.
Huerta, A., & Liu, W. K. (2016). Viscous flow with large free surface motion. Computer
methods in applied mechanics and engineering, 69(3), 277-324.
Parker, G. W. (2017). Projectile motion with air resistance quadratic in the speed. American
Journal of Physics, 45(7), 606-610.