University Project: Transient Response of 1 DoF System Analysis
VerifiedAdded on 2023/06/11
|19
|5903
|331
Homework Assignment
AI Summary
This assignment analyzes the forced transient response of a 1 Degree of Freedom (1 DoF) system subjected to an aperiodic input force. The solution begins by establishing the homogeneous differential equation of the mass-spring-damper system and determining its natural frequency, damping ratio, and damped frequency. The transfer function is defined, and a pole-zero plot is generated to analyze system stability. The aperiodic input force is then defined, and the transient response is solved using three methods: Laplace transform, numerical convolution, and MATLAB. The Laplace transform method involves transforming the differential equation into the s-domain, solving for the displacement, and performing an inverse Laplace transform to obtain the time-domain solution. The numerical convolution method calculates the response directly in the time domain by convolving the system's impulse response with the input force. Finally, MATLAB is used to solve the differential equation using dsolve and ode45 functions, providing a graphical representation of the system's response. The assignment compares the results obtained from these different methods. The assignment also includes MATLAB codes and plots to visualize the input force and the system's displacement response.

1 Introduction (5 points)
In this particular assignment the objective is to create a force-transient response of a 1
Degree of freedom system which is excited by an aperiodic input force. Then the
response of the system is solved using Numerical convolution, Laplace transform
method and software solution using MATLAB. In MATLAB dsolve and ode45 function is
used to solve the differential equation of the system in time domain. The system is a
mass-spring and damper system with specific parameters as described in the later
section. The solution of the system is obtained in graphical form via plots in MATLAB
and compared with theoretical solution via analytical methods. The block diagram of
the mass-spring-damper system is given below.
Here, x(t) is the displacement in time t, m is the mass, k is the stiffness coefficient of the
spring and F(t) is the force applied at time t.
In this particular assignment the objective is to create a force-transient response of a 1
Degree of freedom system which is excited by an aperiodic input force. Then the
response of the system is solved using Numerical convolution, Laplace transform
method and software solution using MATLAB. In MATLAB dsolve and ode45 function is
used to solve the differential equation of the system in time domain. The system is a
mass-spring and damper system with specific parameters as described in the later
section. The solution of the system is obtained in graphical form via plots in MATLAB
and compared with theoretical solution via analytical methods. The block diagram of
the mass-spring-damper system is given below.
Here, x(t) is the displacement in time t, m is the mass, k is the stiffness coefficient of the
spring and F(t) is the force applied at time t.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
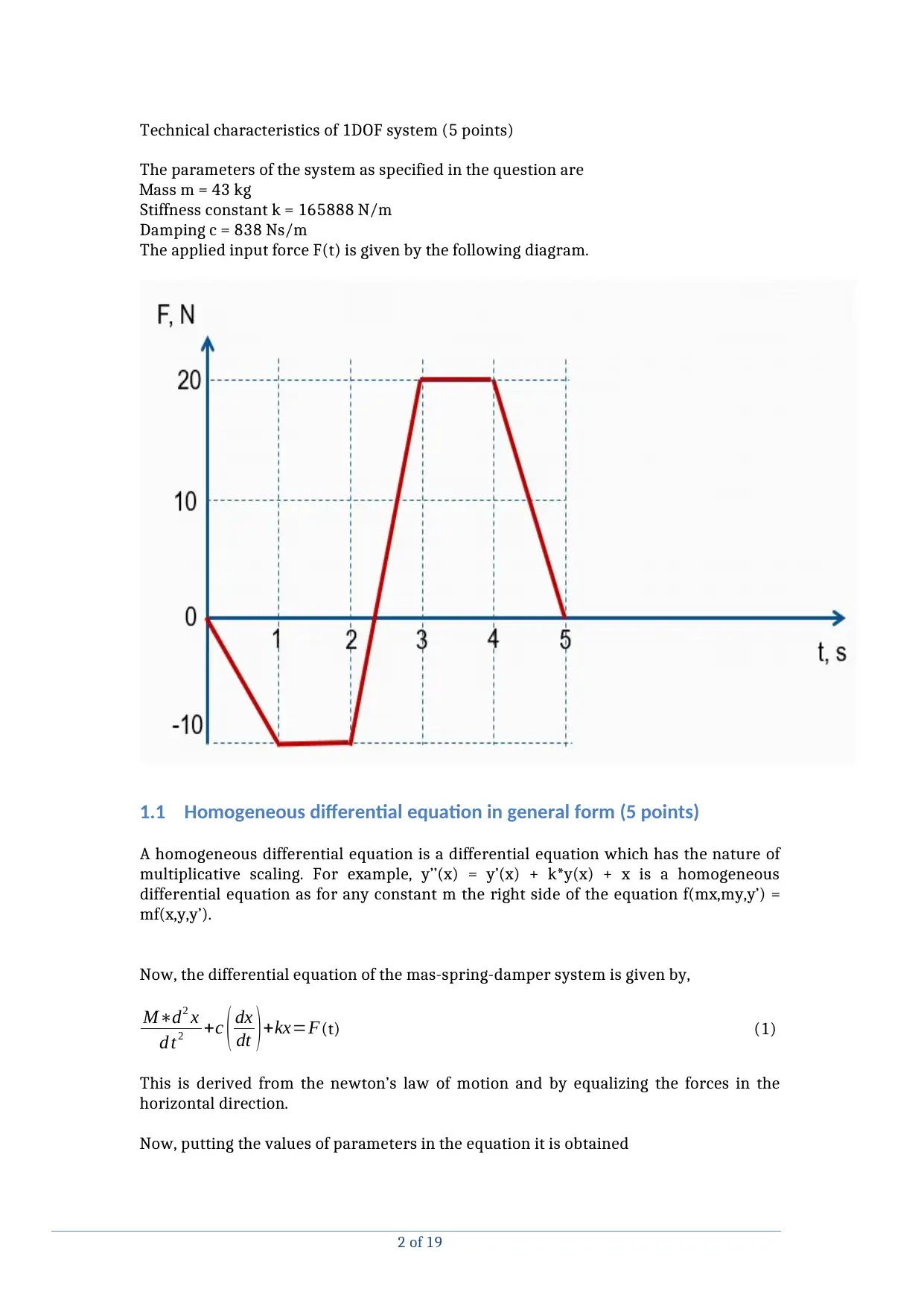
Technical characteristics of 1DOF system (5 points)
The parameters of the system as specified in the question are
Mass m = 43 kg
Stiffness constant k = 165888 N/m
Damping c = 838 Ns/m
The applied input force F(t) is given by the following diagram.
1.1 Homogeneous differential equation in general form (5 points)
A homogeneous differential equation is a differential equation which has the nature of
multiplicative scaling. For example, y’’(x) = y’(x) + k*y(x) + x is a homogeneous
differential equation as for any constant m the right side of the equation f(mx,my,y’) =
mf(x,y,y’).
Now, the differential equation of the mas-spring-damper system is given by,
M∗d2 x
d t 2 +c ( dx
dt ) +kx=F(t) (1)
This is derived from the newton’s law of motion and by equalizing the forces in the
horizontal direction.
Now, putting the values of parameters in the equation it is obtained
2 of 19
The parameters of the system as specified in the question are
Mass m = 43 kg
Stiffness constant k = 165888 N/m
Damping c = 838 Ns/m
The applied input force F(t) is given by the following diagram.
1.1 Homogeneous differential equation in general form (5 points)
A homogeneous differential equation is a differential equation which has the nature of
multiplicative scaling. For example, y’’(x) = y’(x) + k*y(x) + x is a homogeneous
differential equation as for any constant m the right side of the equation f(mx,my,y’) =
mf(x,y,y’).
Now, the differential equation of the mas-spring-damper system is given by,
M∗d2 x
d t 2 +c ( dx
dt ) +kx=F(t) (1)
This is derived from the newton’s law of motion and by equalizing the forces in the
horizontal direction.
Now, putting the values of parameters in the equation it is obtained
2 of 19

43∗d2 x
d t2 +838 ( dx
dt )+165888 x=F(t)
1.2 Find natural frequency, damping ratio and damped frequency if
applicable (5 points)
The natural frequency (wn), damping ratio ( ) and damped frequency (wd) is obtainedζ
by the following method. The natural frequency is the frequency at which the system
tends to oscillate when any of the damping or driving force is absent. The damping ratio
is a dimensionless measure through which the decay of the oscillatory behaviour is
represented after some disturbance has occurred.
Rearranging the equation (1) we get
m ( d2 x
d t 2 ) =F ( t ) – kx – c∗( dx
dt ) (1)
Now, dividing both sides by k we get
m
k ( d2 x
d t2 )= F ( t )
k – x – c
k ∗( dx
dt )
Hence, the natural frequency of the system is
wn = √ k
m= √ 165888
43 =62.1117 rad /sec, damping ratio ( ) =ζ 838
2∗√165888∗43 = 0.1569
The damped frequency wd=62.1117∗√1−0.15692 = 61.3424 rad/sec.
1.3 Define transfer function (5 points)
The transfer function of a system is the ratio of output and input. This is basically a
mathematical function that relates the output of the device to its input. It is also
represented as a graph where the independent scalar input is plotted against the
dependent scalar output. The graph is also known as characteristics curve or the
transfer curve. The transfer function is often represented in s domain.
Now, for obtaining the transfer function of the above system Laplace transform is taken
on both sides of equation (1) assuming the initial conditions as zero.
m s2 X (s)=F ( s ) – k∗X ( s ) – c∗s∗X ( s )
Hence,
X ( s ) ( m s2+ cs+ k )=F ( s ) => X ( s )
F ( s ) = 1
ms2 +cs+k
3 of 19
d t2 +838 ( dx
dt )+165888 x=F(t)
1.2 Find natural frequency, damping ratio and damped frequency if
applicable (5 points)
The natural frequency (wn), damping ratio ( ) and damped frequency (wd) is obtainedζ
by the following method. The natural frequency is the frequency at which the system
tends to oscillate when any of the damping or driving force is absent. The damping ratio
is a dimensionless measure through which the decay of the oscillatory behaviour is
represented after some disturbance has occurred.
Rearranging the equation (1) we get
m ( d2 x
d t 2 ) =F ( t ) – kx – c∗( dx
dt ) (1)
Now, dividing both sides by k we get
m
k ( d2 x
d t2 )= F ( t )
k – x – c
k ∗( dx
dt )
Hence, the natural frequency of the system is
wn = √ k
m= √ 165888
43 =62.1117 rad /sec, damping ratio ( ) =ζ 838
2∗√165888∗43 = 0.1569
The damped frequency wd=62.1117∗√1−0.15692 = 61.3424 rad/sec.
1.3 Define transfer function (5 points)
The transfer function of a system is the ratio of output and input. This is basically a
mathematical function that relates the output of the device to its input. It is also
represented as a graph where the independent scalar input is plotted against the
dependent scalar output. The graph is also known as characteristics curve or the
transfer curve. The transfer function is often represented in s domain.
Now, for obtaining the transfer function of the above system Laplace transform is taken
on both sides of equation (1) assuming the initial conditions as zero.
m s2 X (s)=F ( s ) – k∗X ( s ) – c∗s∗X ( s )
Hence,
X ( s ) ( m s2+ cs+ k )=F ( s ) => X ( s )
F ( s ) = 1
ms2 +cs+k
3 of 19
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Now, putting the values of the parameters
X ( s )
F ( s ) = 1
ms2 +cs+ k = 1
43 s2 +838 s +165888
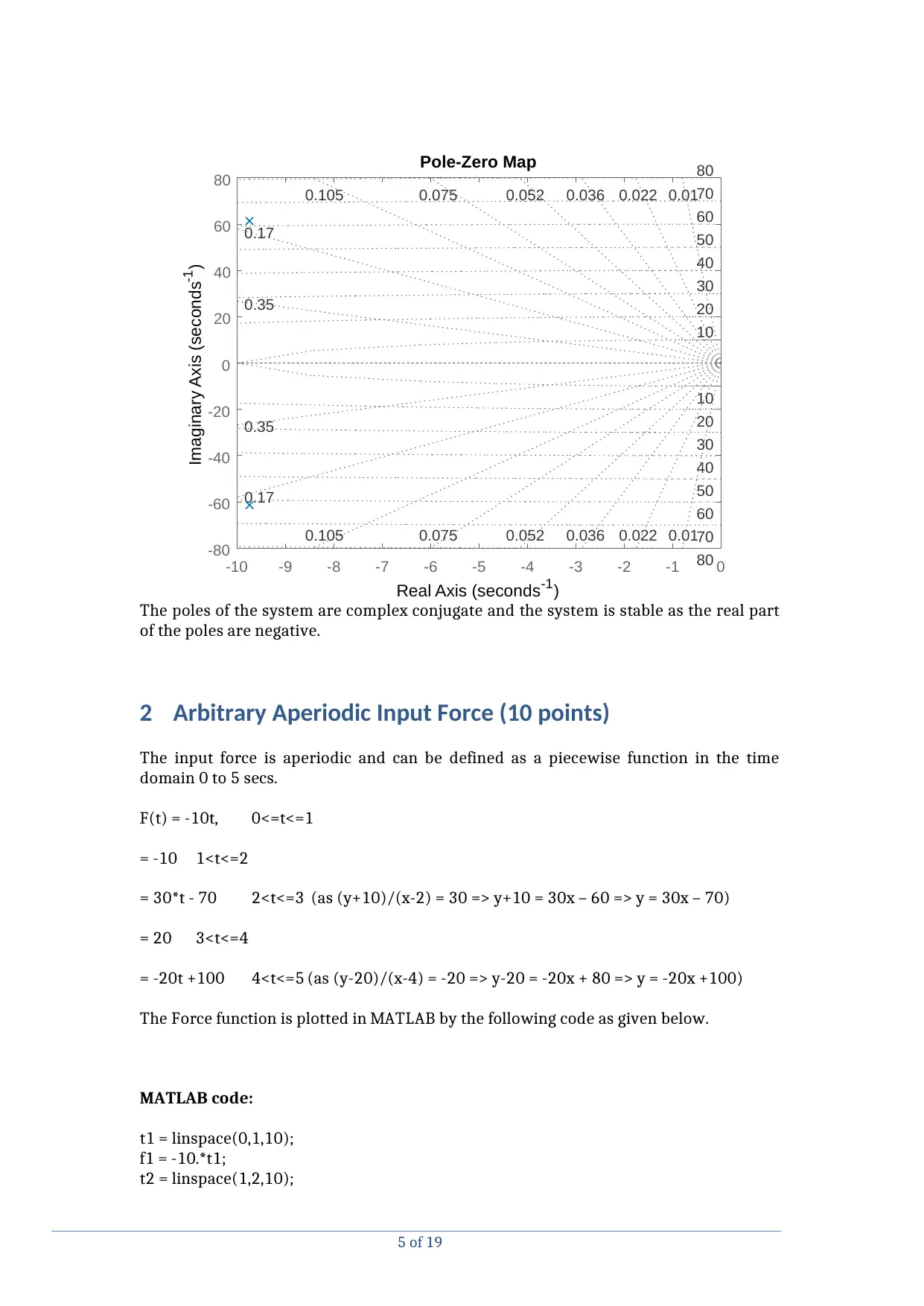
1.4 Plot poles and zeros plot (5 points)
The transfer function has two roots in the denominator. The numerator is 1. Hence, the
system has no zeroes and two poles. The poles can be obtained by pole-zero plot in
MATLAB. The MATLAB code is given below.
MATLAB code:
num = 1; % defining numerator of T.F
den = [43 838 165888]; % defining denominator of T.F
model = tf(num,den); % obtaining transfer function of the system
pzmap(model) % obtaining pole-zero plot
grid on % displaying grid in plot
p = roots(den); % obtaining poles of the system
sprintf('The poles of the system are %g + %gj and %g +
(%gj)',real(p(1)),imag(p(1)),real(p(2)),imag(p(2))) % displaying poles of the system
Output:
polezeroplot
ans =
'The poles of the system are -9.74419 + 61.3426j and -9.74419 + (-61.3426j)'
Plot:
4 of 19
X ( s )
F ( s ) = 1
ms2 +cs+ k = 1
43 s2 +838 s +165888
1.4 Plot poles and zeros plot (5 points)
The transfer function has two roots in the denominator. The numerator is 1. Hence, the
system has no zeroes and two poles. The poles can be obtained by pole-zero plot in
MATLAB. The MATLAB code is given below.
MATLAB code:
num = 1; % defining numerator of T.F
den = [43 838 165888]; % defining denominator of T.F
model = tf(num,den); % obtaining transfer function of the system
pzmap(model) % obtaining pole-zero plot
grid on % displaying grid in plot
p = roots(den); % obtaining poles of the system
sprintf('The poles of the system are %g + %gj and %g +
(%gj)',real(p(1)),imag(p(1)),real(p(2)),imag(p(2))) % displaying poles of the system
Output:
polezeroplot
ans =
'The poles of the system are -9.74419 + 61.3426j and -9.74419 + (-61.3426j)'
Plot:
4 of 19
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0
-80
-60
-40
-20
0
20
40
60
80
70
80
0.01
10
20
30
40
50
0.0220.0360.0520.0750.105
0.17
0.35
0.01
10
20
30
40
50
0.0220.0360.0520.0750.105
0.17
0.35
60
70
80
60
Pole-Zero Map
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
The poles of the system are complex conjugate and the system is stable as the real part
of the poles are negative.
2 Arbitrary Aperiodic Input Force (10 points)
The input force is aperiodic and can be defined as a piecewise function in the time
domain 0 to 5 secs.
F(t) = -10t, 0<=t<=1
= -10 1<t<=2
= 30*t - 70 2<t<=3 (as (y+10)/(x-2) = 30 => y+10 = 30x – 60 => y = 30x – 70)
= 20 3<t<=4
= -20t +100 4<t<=5 (as (y-20)/(x-4) = -20 => y-20 = -20x + 80 => y = -20x +100)
The Force function is plotted in MATLAB by the following code as given below.
MATLAB code:
t1 = linspace(0,1,10);
f1 = -10.*t1;
t2 = linspace(1,2,10);
5 of 19
-80
-60
-40
-20
0
20
40
60
80
70
80
0.01
10
20
30
40
50
0.0220.0360.0520.0750.105
0.17
0.35
0.01
10
20
30
40
50
0.0220.0360.0520.0750.105
0.17
0.35
60
70
80
60
Pole-Zero Map
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
The poles of the system are complex conjugate and the system is stable as the real part
of the poles are negative.
2 Arbitrary Aperiodic Input Force (10 points)
The input force is aperiodic and can be defined as a piecewise function in the time
domain 0 to 5 secs.
F(t) = -10t, 0<=t<=1
= -10 1<t<=2
= 30*t - 70 2<t<=3 (as (y+10)/(x-2) = 30 => y+10 = 30x – 60 => y = 30x – 70)
= 20 3<t<=4
= -20t +100 4<t<=5 (as (y-20)/(x-4) = -20 => y-20 = -20x + 80 => y = -20x +100)
The Force function is plotted in MATLAB by the following code as given below.
MATLAB code:
t1 = linspace(0,1,10);
f1 = -10.*t1;
t2 = linspace(1,2,10);
5 of 19
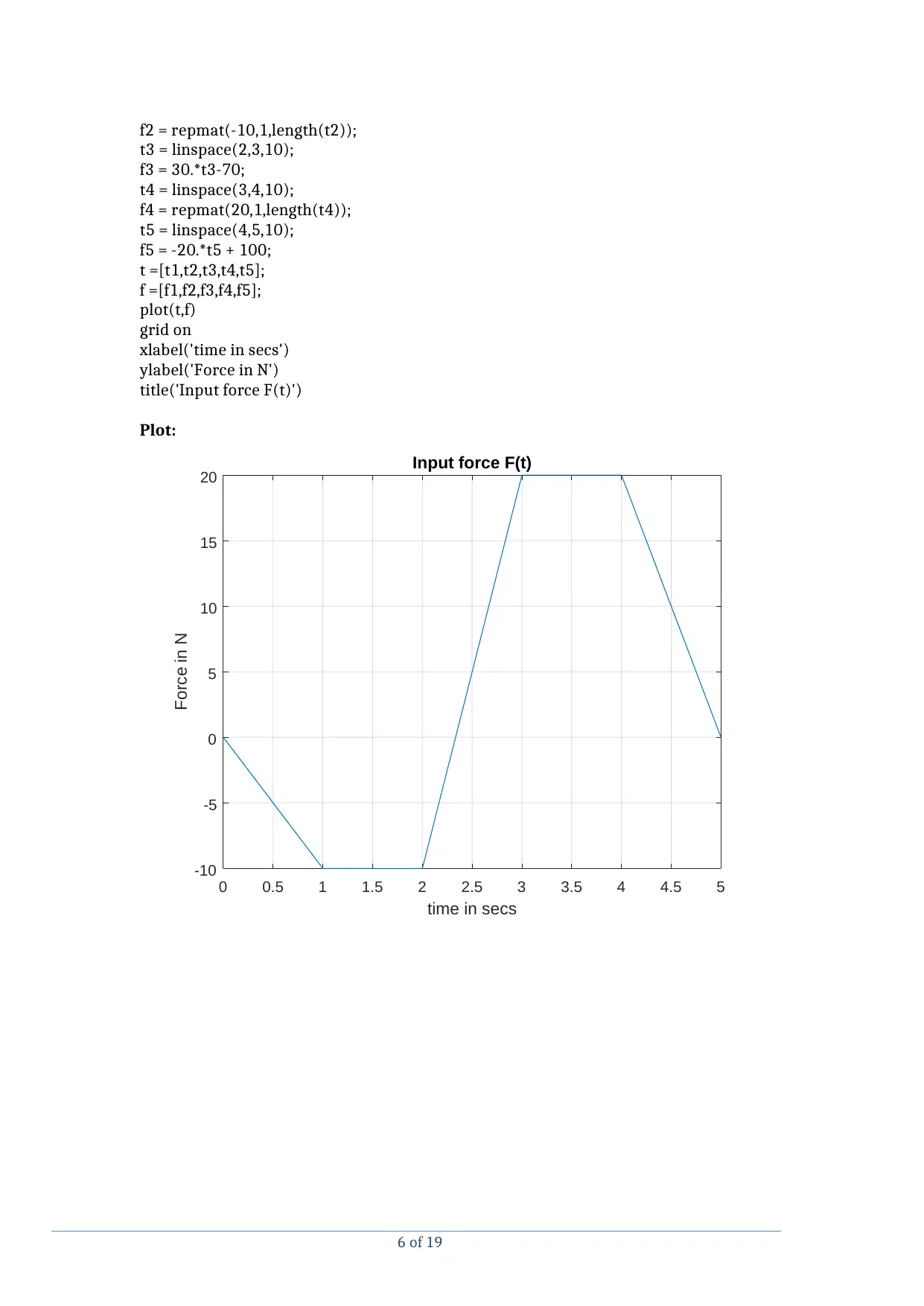
f2 = repmat(-10,1,length(t2));
t3 = linspace(2,3,10);
f3 = 30.*t3-70;
t4 = linspace(3,4,10);
f4 = repmat(20,1,length(t4));
t5 = linspace(4,5,10);
f5 = -20.*t5 + 100;
t =[t1,t2,t3,t4,t5];
f =[f1,f2,f3,f4,f5];
plot(t,f)
grid on
xlabel('time in secs')
ylabel('Force in N')
title('Input force F(t)')
Plot:
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
time in secs
-10
-5
0
5
10
15
20
Force in N
Input force F(t)
6 of 19
t3 = linspace(2,3,10);
f3 = 30.*t3-70;
t4 = linspace(3,4,10);
f4 = repmat(20,1,length(t4));
t5 = linspace(4,5,10);
f5 = -20.*t5 + 100;
t =[t1,t2,t3,t4,t5];
f =[f1,f2,f3,f4,f5];
plot(t,f)
grid on
xlabel('time in secs')
ylabel('Force in N')
title('Input force F(t)')
Plot:
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
time in secs
-10
-5
0
5
10
15
20
Force in N
Input force F(t)
6 of 19
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3 Transient response in Laplace (5 points)
In Laplace transform method the differential equation is converted in s domain and
then inverse Laplace transform is applied to solve the system in time domain. The
method has the advantage that exact solution of the response can be obtained as the
mathematical expression of the response is obtained in inverse Laplace. However, the
disadvantage is that for large and irregular force function the Laplace and inverse
Laplace transform calculation becomes rigorous and thus can’t be applied for real time
systems.
3.1 Model input force (5 points)
The model of the input is defined using piecewise function. The input force here is taken
as continuous function in time t=[0,5] secs. The plot of the input force is given below.
MATLAB code:
t1 = linspace(0,1,10);
f1 = -10.*t1;
t2 = linspace(1,2,10);
f2 = repmat(-10,1,length(t2));
t3 = linspace(2,3,10);
f3 = 30.*t3-70;
t4 = linspace(3,4,10);
f4 = repmat(20,1,length(t4));
t5 = linspace(4,5,10);
f5 = -20.*t5 + 100;
t =[t1,t2,t3,t4,t5];
f =[f1,f2,f3,f4,f5];
plot(t,f)
grid on
xlabel('time in secs')
ylabel('Force in N')
title('Input force F(t)')
7 of 19
In Laplace transform method the differential equation is converted in s domain and
then inverse Laplace transform is applied to solve the system in time domain. The
method has the advantage that exact solution of the response can be obtained as the
mathematical expression of the response is obtained in inverse Laplace. However, the
disadvantage is that for large and irregular force function the Laplace and inverse
Laplace transform calculation becomes rigorous and thus can’t be applied for real time
systems.
3.1 Model input force (5 points)
The model of the input is defined using piecewise function. The input force here is taken
as continuous function in time t=[0,5] secs. The plot of the input force is given below.
MATLAB code:
t1 = linspace(0,1,10);
f1 = -10.*t1;
t2 = linspace(1,2,10);
f2 = repmat(-10,1,length(t2));
t3 = linspace(2,3,10);
f3 = 30.*t3-70;
t4 = linspace(3,4,10);
f4 = repmat(20,1,length(t4));
t5 = linspace(4,5,10);
f5 = -20.*t5 + 100;
t =[t1,t2,t3,t4,t5];
f =[f1,f2,f3,f4,f5];
plot(t,f)
grid on
xlabel('time in secs')
ylabel('Force in N')
title('Input force F(t)')
7 of 19
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
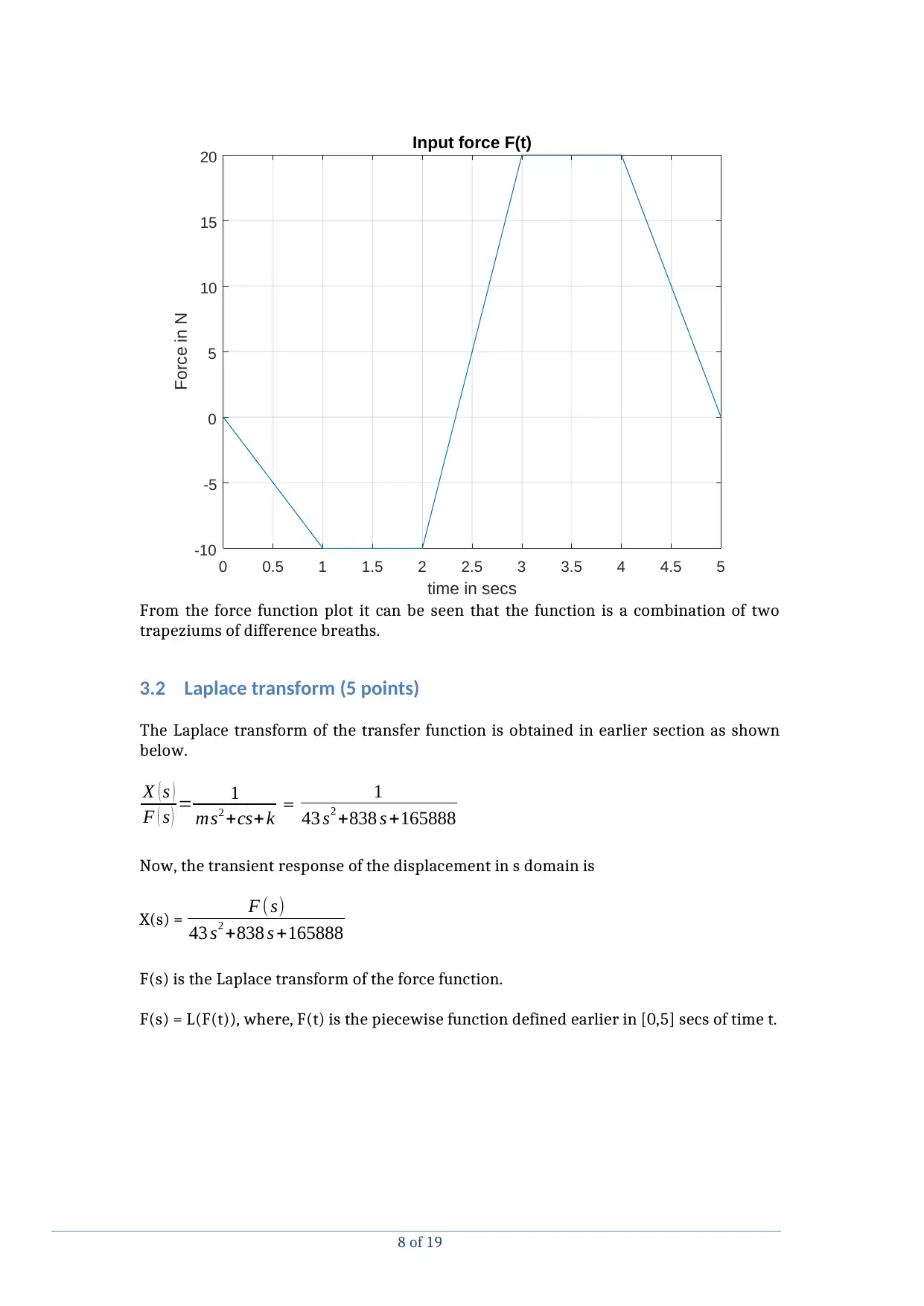
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
time in secs
-10
-5
0
5
10
15
20
Force in N
Input force F(t)
From the force function plot it can be seen that the function is a combination of two
trapeziums of difference breaths.
3.2 Laplace transform (5 points)
The Laplace transform of the transfer function is obtained in earlier section as shown
below.
X ( s )
F ( s ) = 1
ms2 +cs+ k = 1
43 s2 +838 s +165888
Now, the transient response of the displacement in s domain is
X(s) = F ( s)
43 s2 +838 s +165888
F(s) is the Laplace transform of the force function.
F(s) = L(F(t)), where, F(t) is the piecewise function defined earlier in [0,5] secs of time t.
8 of 19
time in secs
-10
-5
0
5
10
15
20
Force in N
Input force F(t)
From the force function plot it can be seen that the function is a combination of two
trapeziums of difference breaths.
3.2 Laplace transform (5 points)
The Laplace transform of the transfer function is obtained in earlier section as shown
below.
X ( s )
F ( s ) = 1
ms2 +cs+ k = 1
43 s2 +838 s +165888
Now, the transient response of the displacement in s domain is
X(s) = F ( s)
43 s2 +838 s +165888
F(s) is the Laplace transform of the force function.
F(s) = L(F(t)), where, F(t) is the piecewise function defined earlier in [0,5] secs of time t.
8 of 19

F(s) = ∫
0
1
−10 te−st dt+∫
1
2
−10 e− st dt+ ∫
2
3
(30 t−70)e−st dt + ∫
3
4
20 e− st dt+
∫
4
5
(−20 t+100)e−st dt = −10 e
(−s ) ( es – s – 1 )
s2 – e (−2 s ) ( 10 es – 10 )
s –
( 10 s – 30 ) e−2 s
s2 – ( 20 s+30 ) e−3 s
s2 + e (−4 s ) ( 20 es−20 )
s + e (−5 s ) ( ( 20 s−20 ) es +20 )
s2
Inverse Laplace (5 points)
Inverse Laplace transform is performed for finding the displacement in time domain.
The Inverse Laplace transform of the large function is computed by MATLAB with
symbolic variable s. The MATLAB code is given below.
MATLAB code:
syms s
F = -10*exp(-s)*(exp(s) - s - 1)/s^2 - exp(-2*s)*(10*exp(s) - 10)/s - (10*s - 30)*exp(-
2*s)/s^2 - (20*s+30)*exp(-3*s)/s^2 + exp(-4*s)*(20*exp(s) - 20)/s + exp(-5*s)*((20*s-
20)*exp(s) + 20)/s^2;
tfunc = 1/(43*s^2 + 838*s + 165888);
X = F/tfunc;
solXt = ilaplace(X)
Output:
inverselaplace
solXt =
430*dirac(t - 1) - 1658880*t + 1290*dirac(t - 2) - 1290*dirac(t - 3) - 860*dirac(t - 4) +
860*dirac(t - 5) + 8380*heaviside(t - 1) + 25140*heaviside(t - 2) - 25140*heaviside(t -
3) - 16760*heaviside(t - 4) + 16760*heaviside(t - 5) - 430*dirac(t) +
1658880*heaviside(t - 1)*(t - 1) + 4976640*heaviside(t - 2)*(t - 2) -
4976640*heaviside(t - 3)*(t - 3) - 3317760*heaviside(t - 4)*(t - 4) +
3317760*heaviside(t - 5)*(t - 5) - 8380
3.3 Graph (5 points)
Now, the solution of displacement obtained in time domain is plotted using MATLAB for
a unit step response as given below.
MATLAB code:
t = 0:0.001:5;
solXt = 430.*dirac(t - 1) - 1658880.*t + 1290.*dirac(t - 2) - 1290.*dirac(t - 3) -
860.*dirac(t - 4) + 860.*dirac(t - 5) + 8380.*heaviside(t - 1) + 25140.*heaviside(t - 2) -
9 of 19
0
1
−10 te−st dt+∫
1
2
−10 e− st dt+ ∫
2
3
(30 t−70)e−st dt + ∫
3
4
20 e− st dt+
∫
4
5
(−20 t+100)e−st dt = −10 e
(−s ) ( es – s – 1 )
s2 – e (−2 s ) ( 10 es – 10 )
s –
( 10 s – 30 ) e−2 s
s2 – ( 20 s+30 ) e−3 s
s2 + e (−4 s ) ( 20 es−20 )
s + e (−5 s ) ( ( 20 s−20 ) es +20 )
s2
Inverse Laplace (5 points)
Inverse Laplace transform is performed for finding the displacement in time domain.
The Inverse Laplace transform of the large function is computed by MATLAB with
symbolic variable s. The MATLAB code is given below.
MATLAB code:
syms s
F = -10*exp(-s)*(exp(s) - s - 1)/s^2 - exp(-2*s)*(10*exp(s) - 10)/s - (10*s - 30)*exp(-
2*s)/s^2 - (20*s+30)*exp(-3*s)/s^2 + exp(-4*s)*(20*exp(s) - 20)/s + exp(-5*s)*((20*s-
20)*exp(s) + 20)/s^2;
tfunc = 1/(43*s^2 + 838*s + 165888);
X = F/tfunc;
solXt = ilaplace(X)
Output:
inverselaplace
solXt =
430*dirac(t - 1) - 1658880*t + 1290*dirac(t - 2) - 1290*dirac(t - 3) - 860*dirac(t - 4) +
860*dirac(t - 5) + 8380*heaviside(t - 1) + 25140*heaviside(t - 2) - 25140*heaviside(t -
3) - 16760*heaviside(t - 4) + 16760*heaviside(t - 5) - 430*dirac(t) +
1658880*heaviside(t - 1)*(t - 1) + 4976640*heaviside(t - 2)*(t - 2) -
4976640*heaviside(t - 3)*(t - 3) - 3317760*heaviside(t - 4)*(t - 4) +
3317760*heaviside(t - 5)*(t - 5) - 8380
3.3 Graph (5 points)
Now, the solution of displacement obtained in time domain is plotted using MATLAB for
a unit step response as given below.
MATLAB code:
t = 0:0.001:5;
solXt = 430.*dirac(t - 1) - 1658880.*t + 1290.*dirac(t - 2) - 1290.*dirac(t - 3) -
860.*dirac(t - 4) + 860.*dirac(t - 5) + 8380.*heaviside(t - 1) + 25140.*heaviside(t - 2) -
9 of 19
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
25140.*heaviside(t - 3) - 16760.*heaviside(t - 4) + 16760.*heaviside(t - 5) -
430.*dirac(t) + 1658880.*heaviside(t - 1).*(t - 1) + 4976640.*heaviside(t - 2).*(t - 2) -
4976640.*heaviside(t - 3).*(t - 3) - 3317760.*heaviside(t - 4).*(t - 4) +
3317760.*heaviside(t - 5).*(t - 5) - 8380;
plot(t,solXt)
xlabel('time t in 0 to 5 secs')
ylabel('Displacement x(t) at time t in meters')
title('Plot of the solution displacement at time t')
Plot:
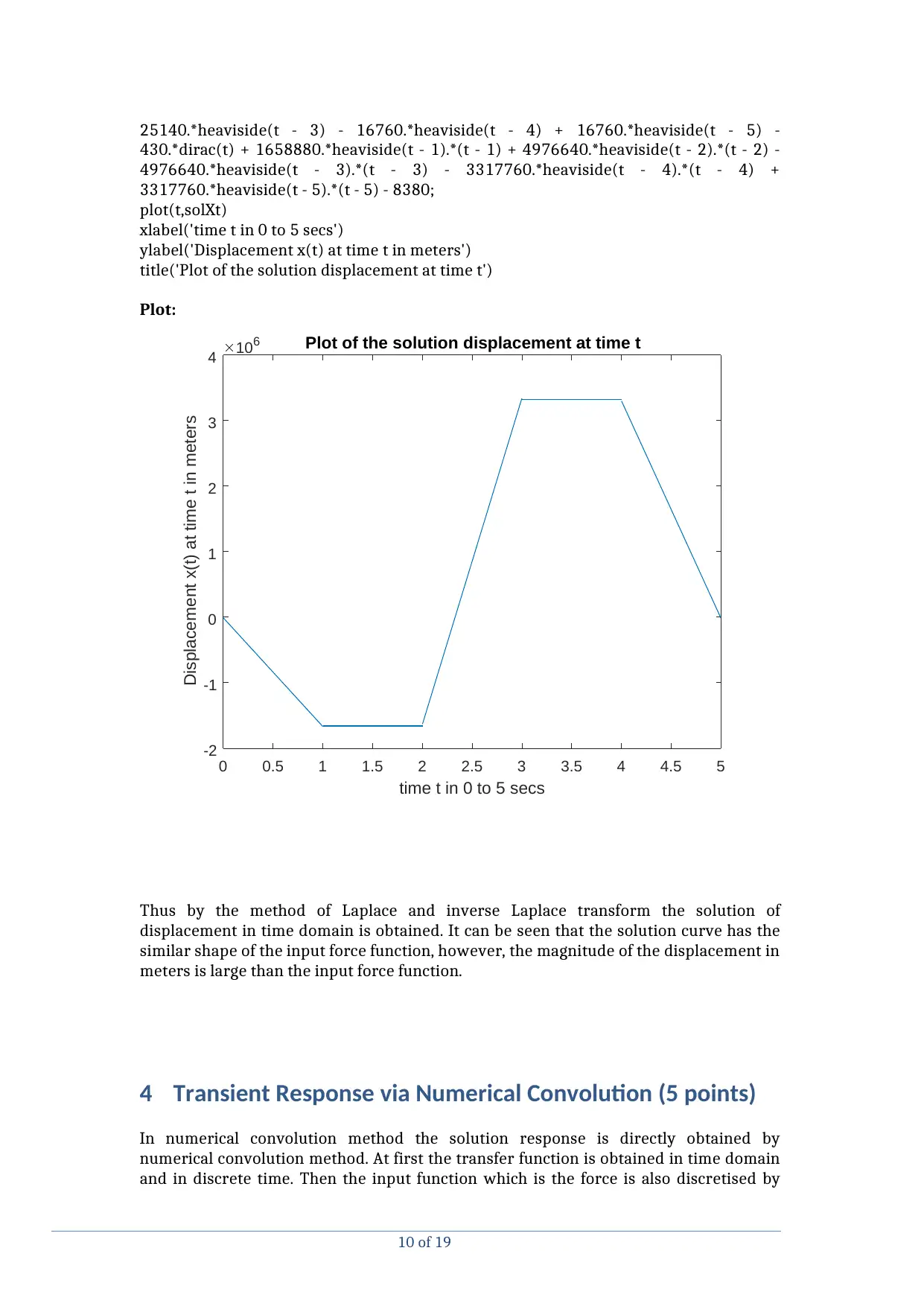
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
time t in 0 to 5 secs
-2
-1
0
1
2
3
4
Displacement x(t) at time t in meters
106 Plot of the solution displacement at time t
Thus by the method of Laplace and inverse Laplace transform the solution of
displacement in time domain is obtained. It can be seen that the solution curve has the
similar shape of the input force function, however, the magnitude of the displacement in
meters is large than the input force function.
4 Transient Response via Numerical Convolution (5 points)
In numerical convolution method the solution response is directly obtained by
numerical convolution method. At first the transfer function is obtained in time domain
and in discrete time. Then the input function which is the force is also discretised by
10 of 19
430.*dirac(t) + 1658880.*heaviside(t - 1).*(t - 1) + 4976640.*heaviside(t - 2).*(t - 2) -
4976640.*heaviside(t - 3).*(t - 3) - 3317760.*heaviside(t - 4).*(t - 4) +
3317760.*heaviside(t - 5).*(t - 5) - 8380;
plot(t,solXt)
xlabel('time t in 0 to 5 secs')
ylabel('Displacement x(t) at time t in meters')
title('Plot of the solution displacement at time t')
Plot:
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
time t in 0 to 5 secs
-2
-1
0
1
2
3
4
Displacement x(t) at time t in meters
106 Plot of the solution displacement at time t
Thus by the method of Laplace and inverse Laplace transform the solution of
displacement in time domain is obtained. It can be seen that the solution curve has the
similar shape of the input force function, however, the magnitude of the displacement in
meters is large than the input force function.
4 Transient Response via Numerical Convolution (5 points)
In numerical convolution method the solution response is directly obtained by
numerical convolution method. At first the transfer function is obtained in time domain
and in discrete time. Then the input function which is the force is also discretised by
10 of 19
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

impulse functions. After that the convolution is performed between the two discrete
time signals and the solution is obtained in time domain.
Mathematically, numerical convolution is expressed as
X(s) = F(s)TF(s) (in s domain)
x[t] = F[t]*TF[t] (in time domain)
The advantage of this particular method is that when the input function is not
symmetric then numerical convolution do not require the knowledge of the
mathematical expression of input function and response can be obtained in discrete
points. Disadvantage of this method is that as the signals are discretised and solution is
obtained is discrete time hence there is some error introduced compared to continuous
time solution.
4.1 Model input force (5 points)
Here, the force input is discretised by several impulse functions in the time domain of 0
to 15 seconds. If the system is overdamped then the step size of time t can be taken as
large as 0.1 as the system will not have oscillations. However, when the system is
underdamped then the step size of t needs to be as small as 0.01 as large values will give
much error as the system has many oscillations.
MATLAB code:
t1 = linspace(0,1,10);
f1 = -10.*t1;
t2 = linspace(1,2,10);
f2 = repmat(-10,1,length(t2));
t3 = linspace(2,3,10);
f3 = 30.*t3-70;
t4 = linspace(3,4,10);
f4 = repmat(20,1,length(t4));
t5 = linspace(4,5,10);
f5 = -20.*t5 + 100;
t6 = 5:0.1:15;
t =[t1,t2,t3,t4,t5,t6];
f =[f1,f2,f3,f4,f5,zeros(1,length(t6))];
stem(t,f)
xlabel('Discrete time t')
ylabel('Force by impulses')
title('Discretized Force by impulse function')
Plot:
11 of 19
time signals and the solution is obtained in time domain.
Mathematically, numerical convolution is expressed as
X(s) = F(s)TF(s) (in s domain)
x[t] = F[t]*TF[t] (in time domain)
The advantage of this particular method is that when the input function is not
symmetric then numerical convolution do not require the knowledge of the
mathematical expression of input function and response can be obtained in discrete
points. Disadvantage of this method is that as the signals are discretised and solution is
obtained is discrete time hence there is some error introduced compared to continuous
time solution.
4.1 Model input force (5 points)
Here, the force input is discretised by several impulse functions in the time domain of 0
to 15 seconds. If the system is overdamped then the step size of time t can be taken as
large as 0.1 as the system will not have oscillations. However, when the system is
underdamped then the step size of t needs to be as small as 0.01 as large values will give
much error as the system has many oscillations.
MATLAB code:
t1 = linspace(0,1,10);
f1 = -10.*t1;
t2 = linspace(1,2,10);
f2 = repmat(-10,1,length(t2));
t3 = linspace(2,3,10);
f3 = 30.*t3-70;
t4 = linspace(3,4,10);
f4 = repmat(20,1,length(t4));
t5 = linspace(4,5,10);
f5 = -20.*t5 + 100;
t6 = 5:0.1:15;
t =[t1,t2,t3,t4,t5,t6];
f =[f1,f2,f3,f4,f5,zeros(1,length(t6))];
stem(t,f)
xlabel('Discrete time t')
ylabel('Force by impulses')
title('Discretized Force by impulse function')
Plot:
11 of 19
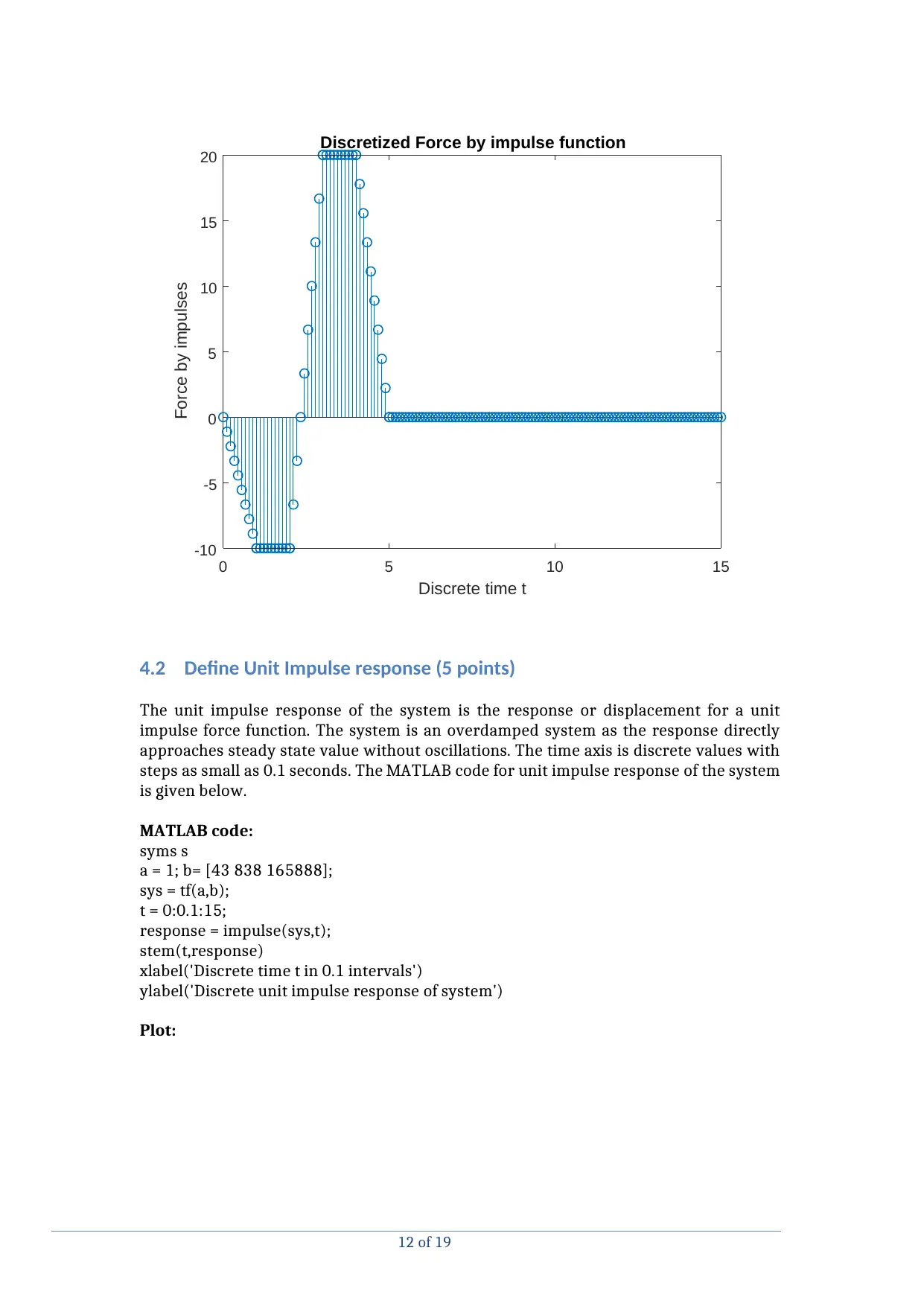
-10
-5
0
5
10
15
20
Force by impulses
Discretized Force by impulse function
0 5 10 15
Discrete time t
4.2 Define Unit Impulse response (5 points)
The unit impulse response of the system is the response or displacement for a unit
impulse force function. The system is an overdamped system as the response directly
approaches steady state value without oscillations. The time axis is discrete values with
steps as small as 0.1 seconds. The MATLAB code for unit impulse response of the system
is given below.
MATLAB code:
syms s
a = 1; b= [43 838 165888];
sys = tf(a,b);
t = 0:0.1:15;
response = impulse(sys,t);
stem(t,response)
xlabel('Discrete time t in 0.1 intervals')
ylabel('Discrete unit impulse response of system')
Plot:
12 of 19
-5
0
5
10
15
20
Force by impulses
Discretized Force by impulse function
0 5 10 15
Discrete time t
4.2 Define Unit Impulse response (5 points)
The unit impulse response of the system is the response or displacement for a unit
impulse force function. The system is an overdamped system as the response directly
approaches steady state value without oscillations. The time axis is discrete values with
steps as small as 0.1 seconds. The MATLAB code for unit impulse response of the system
is given below.
MATLAB code:
syms s
a = 1; b= [43 838 165888];
sys = tf(a,b);
t = 0:0.1:15;
response = impulse(sys,t);
stem(t,response)
xlabel('Discrete time t in 0.1 intervals')
ylabel('Discrete unit impulse response of system')
Plot:
12 of 19
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 19
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





