Forecasting Future GDP of British Columbia using ARIMA Model

This paper aims to forecast the future GDP of British Columbia using the ARIMA model. It discusses the importance of forecasting and its application in various fields. The methodology, data, and results of the study are presented, along with the conclusions drawn. The study provides insights into the forecasting of GDP and its implications for decision-making.

Forecasting the future GDP of British Columbia
using ARIMA model on Eviews
Student Name ******
Abstract
Basically, forecasting are important and it continually made in business, fund,
financial matters, government, and numerous different fields, and much relies on them.
Similarly, there are there are good and bad ways to forecast. The forecasting is used to
provide the great ways for current, quantitative, economic and statistical strategies for
evaluating and producing the forecasts. Forecasts are settled on to direct decisions in an
variety of fields. Gross Domestic Product (GDP) of a nation is the cash estimation of all
goods and administrations created by every one of the enterprises inside the bounds of a
nation in a year. It speaks to the total measurement of all financial action. The execution of
economy can be forecast with the assistance of GDP. As indicated by Euro stat, there are
three manners by which the GDP of a nation can be forecasts. This paper aims to displaying
and determining forecasting GDP of British Columbia utilizing ARIMA model. Here
analyzed by time series method. Auto Correlation Function (ACF) and Partial Auto
Correlation Function (PACF) are will calculated. Proper Box-Jenkins Auto Regressive
Integrated Moving Average (ARIMA) demonstrates the forecasting the future GDP of British
Columbia. Legitimacy of the model was tested using standard statistical techniques. And,
ARIMA model is used to show were utilized to forecasting zone and creation of British
Columbia for future years.
Keywords: Forecast, GDP, ACF, PACF and ARIMA
1

Introduction
The forecasting is used to provide the great ways for current, quantitative, economic
and statistical strategies for evaluating and producing the forecasts. Forecasts are settled on to
direct decisions in a variety of fields. Gross Domestic Product (GDP) of a nation is the cash
estimation of all goods and administrations created by every one of the enterprises inside the
bounds of a nation in a year. The execution of economy can be forecast with the assistance of
GDP. This paper aims to displaying and determining forecasting GDP of British Columbia
utilizing ARIMA model. Here analyzed by time series method. Auto Correlation Function
(ACF) and Partial Auto Correlation Function (PACF) are will calculated. Proper Box-Jenkins
Auto Regressive Integrated Moving Average (ARIMA) demonstrates the forecasting the
future GDP of British Columbia. Legitimacy of the model was tested using standard
statistical techniques. And, ARIMA model is used to show were utilized to forecasting zone
and creation of British Columbia for future years.
Research Objectives
1. To test the stationary in the data of GDP using the Augmented Dickey – Fullers unit
root test over the period.
2. To study Auto correlation in the observed series of GDP ACF and PACF values and
correlogram will be used to measure the AR and MA to predict which past series is a
fitter model for future value prediction.
3. To test the model validity statically a portmanteau test of Independence i.e. the BDS
test for time-based dependence in a series will be applied.
4. Finally Forecast the GDP for the next ten years using ARIMA Model along with the
upper control level (UCL) and the lower control level (LCL).
Literature Review
According to this paper (Dritsaki, 2015), the ARIMA model has be used extensively
by many researchers. This method is used to highlight the future rates of GDP. It easily
examines the forecasting of GDP growth rate for India using the ARIMA model. This model
is used to predicted the values follow an increasing the trend for a years. It establishes the
stationary of time series. Result of this paper is used to provide the policy makers to
formulate the effective policies for attracting the foreign direct investment. It also helpful the
2

managerial business executive for implementing or taking decision concerned with the
expansion of the existing business.
Methodology
The GDP data was collected over the time period from 1997 to 2017 were used for
forecasting the future values using Auto Regressive Integrated Moving Average (ARIMA)
models. The ARIMA procedure is likewise called as Box-Jenkins approach. The Box-Jenkins
method is worried about fitting an ARIMA model to a given data of information. The
objective in fitting ARIMA model is to distinguish the stochastic procedure of the time series
and predicted the future values correctly. These strategies have additionally been helpful in
numerous sorts of circumstances which include the working of models for discrete time series
and dynamic frameworks. Anyway this technique is not useful for seasonal series with a large
random component.
Data Description
The GDP data was collected over the time period from 1997 to 2017. The provided data was
contains the information about the forecast the GDP growth for the province of British
Columbia based on the overall annual expenditure. It is illustrated as below (Camacho &
Martinez-Martin, 2013).
3

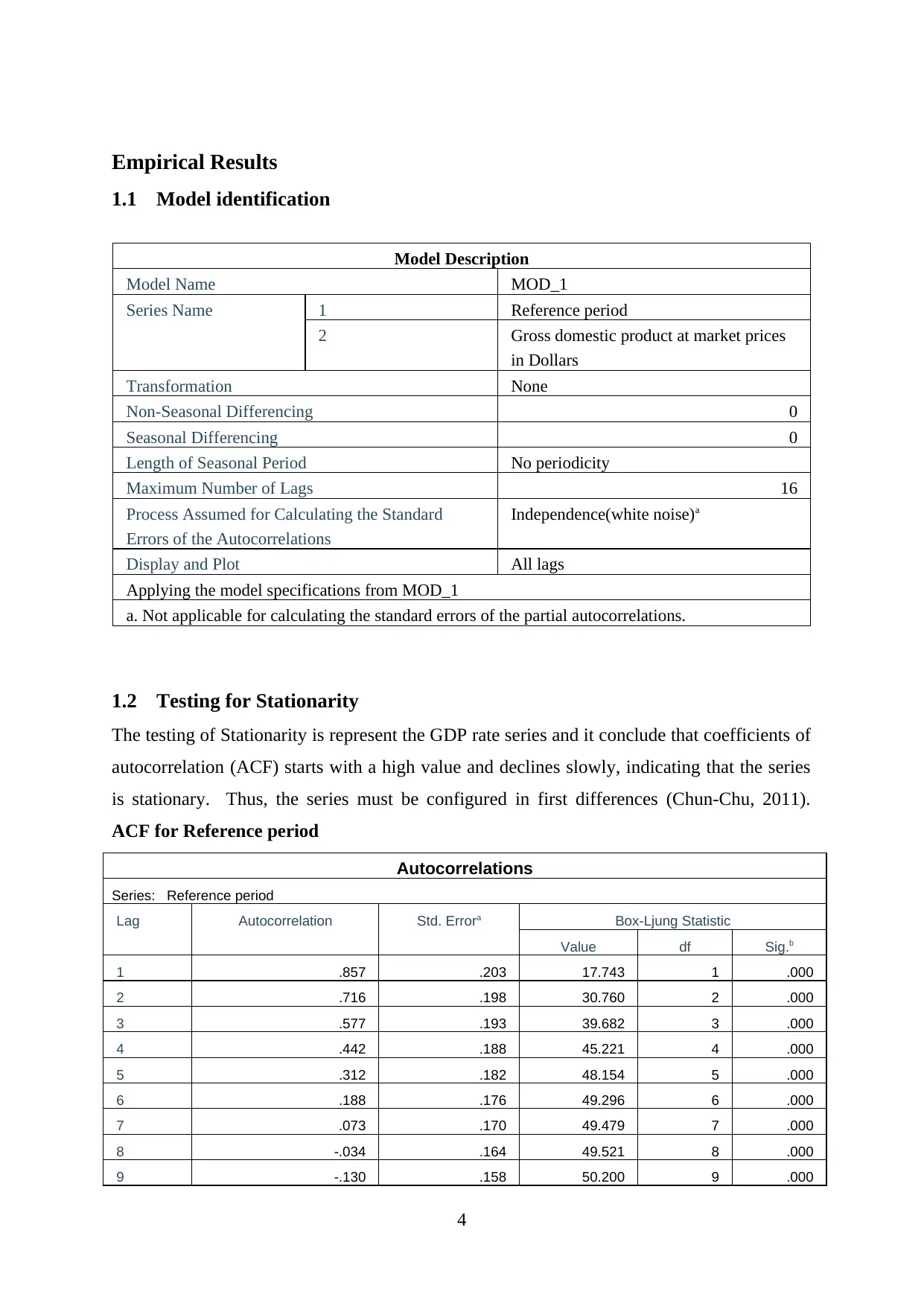
Empirical Results
1.1 Model identification
Model Description
Model Name MOD_1
Series Name 1 Reference period
2 Gross domestic product at market prices
in Dollars
Transformation None
Non-Seasonal Differencing 0
Seasonal Differencing 0
Length of Seasonal Period No periodicity
Maximum Number of Lags 16
Process Assumed for Calculating the Standard
Errors of the Autocorrelations
Independence(white noise)a
Display and Plot All lags
Applying the model specifications from MOD_1
a. Not applicable for calculating the standard errors of the partial autocorrelations.
1.2 Testing for Stationarity
The testing of Stationarity is represent the GDP rate series and it conclude that coefficients of
autocorrelation (ACF) starts with a high value and declines slowly, indicating that the series
is stationary. Thus, the series must be configured in first differences (Chun-Chu, 2011).
ACF for Reference period
Autocorrelations
Series: Reference period
Lag Autocorrelation Std. Errora Box-Ljung Statistic
Value df Sig.b
1 .857 .203 17.743 1 .000
2 .716 .198 30.760 2 .000
3 .577 .193 39.682 3 .000
4 .442 .188 45.221 4 .000
5 .312 .182 48.154 5 .000
6 .188 .176 49.296 6 .000
7 .073 .170 49.479 7 .000
8 -.034 .164 49.521 8 .000
9 -.130 .158 50.200 9 .000
4

10 -.214 .151 52.216 10 .000
11 -.286 .144 56.159 11 .000
12 -.343 .137 62.467 12 .000
13 -.384 .129 71.389 13 .000
14 -.409 .120 82.937 14 .000
15 -.416 .111 96.840 15 .000
16 -.403 .102 112.497 16 .000
a. The underlying process assumed is independence (white noise).
b. Based on the asymptotic chi-square approximation.
ACF for Gross domestic product at market prices in Dollars
Autocorrelations
Series: Gross domestic product at market prices in Dollars
Lag Autocorrelation Std. Errora Box-Ljung Statistic
Value df Sig.b
1 .842 .203 17.108 1 .000
2 .686 .198 29.065 2 .000
3 .541 .193 36.929 3 .000
4 .408 .188 41.649 4 .000
5 .282 .182 44.044 5 .000
6 .167 .176 44.941 6 .000
7 .058 .170 45.056 7 .000
8 -.032 .164 45.094 8 .000
9 -.097 .158 45.470 9 .000
10 -.168 .151 46.713 10 .000
11 -.236 .144 49.394 11 .000
12 -.298 .137 54.152 12 .000
13 -.363 .129 62.094 13 .000
14 -.398 .120 73.047 14 .000
15 -.409 .111 86.482 15 .000
16 -.403 .102 102.134 16 .000
a. The underlying process assumed is independence (white noise).
b. Based on the asymptotic chi-square approximation.
PACF for Reference period
5

Partial Autocorrelations
Series: Reference period
Lag Partial Autocorrelation Std. Error
1 .857 .218
2 -.072 .218
3 -.073 .218
4 -.073 .218
5 -.074 .218
6 -.074 .218
7 -.074 .218
8 -.073 .218
9 -.072 .218
10 -.070 .218
11 -.066 .218
12 -.061 .218
13 -.054 .218
14 -.044 .218
15 -.031 .218
16 -.014 .218
PACF for Gross domestic product at market prices in Dollars
Partial Autocorrelations
Series: Gross domestic product at market prices in Dollars
Lag Partial Autocorrelation Std. Error
1 .842 .218
2 -.078 .218
3 -.053 .218
4 -.057 .218
5 -.067 .218
6 -.058 .218
7 -.079 .218
8 -.035 .218
9 -.010 .218
10 -.109 .218
11 -.080 .218
12 -.085 .218
13 -.121 .218
14 -.020 .218
6

15 -.019 .218
16 -.028 .218
1.3 ARIMA model
Subsequent to making the GDP series stationary the autocorrelation and partial
autocorrelation function were utilized. By examining the PACF values and correlogram term
AR and MA was observed to be fit for forecasts. The ARMA parameters were distinguished
utilizing Autocorrelation and Partial Autocorrelation Functions. It is illustrated as below
(Fildes & Allen, 2011).
Model Description
Model Type
Model ID Gross domestic product at
market prices in Dollars
Model_1 ARIMA(0,1,0)
Residual ACF Summary
Lag Mean SE Minim
um
Maxim
um
Percentile
5 10 25 50 75 90 95
Lag
1
.200 . .200 .200 .200 .200 .200 .200 .200 .200 .200
Lag
2
-.101 . -.101 -.101 -.101 -.101 -.101 -.101 -.101 -.101 -.101
Lag
3
-.134 . -.134 -.134 -.134 -.134 -.134 -.134 -.134 -.134 -.134
Lag
4
-.250 . -.250 -.250 -.250 -.250 -.250 -.250 -.250 -.250 -.250
Lag
5
-.157 . -.157 -.157 -.157 -.157 -.157 -.157 -.157 -.157 -.157
Lag
6
.034 . .034 .034 .034 .034 .034 .034 .034 .034 .034
Lag
7
-.119 . -.119 -.119 -.119 -.119 -.119 -.119 -.119 -.119 -.119
Lag
8
-.091 . -.091 -.091 -.091 -.091 -.091 -.091 -.091 -.091 -.091
Lag
9
-.121 . -.121 -.121 -.121 -.121 -.121 -.121 -.121 -.121 -.121
Lag
10
.119 . .119 .119 .119 .119 .119 .119 .119 .119 .119
Lag .257 . .257 .257 .257 .257 .257 .257 .257 .257 .257
7

11
Lag
12
.108 . .108 .108 .108 .108 .108 .108 .108 .108 .108
Lag
13
-.066 . -.066 -.066 -.066 -.066 -.066 -.066 -.066 -.066 -.066
Lag
14
.018 . .018 .018 .018 .018 .018 .018 .018 .018 .018
Lag
15
-.022 . -.022 -.022 -.022 -.022 -.022 -.022 -.022 -.022 -.022
Lag
16
-.109 . -.109 -.109 -.109 -.109 -.109 -.109 -.109 -.109 -.109
Lag
17
.040 . .040 .040 .040 .040 .040 .040 .040 .040 .040
Lag
18
-.040 . -.040 -.040 -.040 -.040 -.040 -.040 -.040 -.040 -.040
Lag
19
-.068 . -.068 -.068 -.068 -.068 -.068 -.068 -.068 -.068 -.068
Residual PACF Summary
Lag Mean SE Minim
um
Maxim
um
Percentile
5 10 25 50 75 90 95
Lag
1
.200 . .200 .200 .200 .200 .200 .200 .200 .200 .200
Lag
2
-.146 . -.146 -.146 -.146 -.146 -.146 -.146 -.146 -.146 -.146
Lag
3
-.087 . -.087 -.087 -.087 -.087 -.087 -.087 -.087 -.087 -.087
Lag
4
-.232 . -.232 -.232 -.232 -.232 -.232 -.232 -.232 -.232 -.232
Lag
5
-.097 . -.097 -.097 -.097 -.097 -.097 -.097 -.097 -.097 -.097
Lag
6
.015 . .015 .015 .015 .015 .015 .015 .015 .015 .015
Lag
7
-.233 . -.233 -.233 -.233 -.233 -.233 -.233 -.233 -.233 -.233
Lag
8
-.121 . -.121 -.121 -.121 -.121 -.121 -.121 -.121 -.121 -.121
Lag
9
-.236 . -.236 -.236 -.236 -.236 -.236 -.236 -.236 -.236 -.236
Lag
10
.109 . .109 .109 .109 .109 .109 .109 .109 .109 .109
8

Lag
11
.091 . .091 .091 .091 .091 .091 .091 .091 .091 .091
Lag
12
-.064 . -.064 -.064 -.064 -.064 -.064 -.064 -.064 -.064 -.064
Lag
13
-.126 . -.126 -.126 -.126 -.126 -.126 -.126 -.126 -.126 -.126
Lag
14
.084 . .084 .084 .084 .084 .084 .084 .084 .084 .084
Lag
15
.079 . .079 .079 .079 .079 .079 .079 .079 .079 .079
Lag
16
-.153 . -.153 -.153 -.153 -.153 -.153 -.153 -.153 -.153 -.153
Lag
17
.055 . .055 .055 .055 .055 .055 .055 .055 .055 .055
Lag
18
-.052 . -.052 -.052 -.052 -.052 -.052 -.052 -.052 -.052 -.052
Lag
19
.082 . .082 .082 .082 .082 .082 .082 .082 .082 .082
Model Statistics
Model Number of
Predictors
Model Fit
statistics
Ljung-Box Q(18) Number of
Outliers
Stationary R-
squared
Statistics DF Sig.
Gross domestic product at
market prices in Dollars-
Model_1
0 2.220E-16 12.190 18 .837 0
1.4 Model Validity
Model validity is illustrated as below.
9

1.5 GDP Forecast
Final GDP Forecast values for Forecasting the future GDP of British Columbia is illustrated
as below (Şen Doğan & Midiliç, 2018).
Reference
period
Gross domestic product at
market prices in Dollars
(Predicted Values)
LCL UCL
2018 262158 255011 269306
2019 267441 257333 277550
2020 272725 260344 285105
2021 278008 263712 292303
2022 283291 267308 299274
2023 288574 271066 306082
2024 293857 274946 312768
2025 299141 278924 319357
2026 304424 282981 325867
2027 309707 287104 332310
10

Conclusions and Future Research
This project was successfully predicted, displayed the GDP forecast of British
Columbia future utilizing by using the ARIMA model. The predicted value analyzed by time
series method. The Auto Correlation Function (ACF) and Partial Auto Correlation Function
(PACF) are effectively calculated. Used the Proper Box-Jenkins Auto Regressive Integrated
Moving Average (ARIMA) successfully demonstrated the forecasting the future GDP of
British Columbia. Legitimacy of the model was effectively tested by using standard statistical
techniques. And, ARIMA model is used to display the forecasting zone and creation of
British Columbia for future years.
References
Camacho, M., & Martinez-Martin, J. (2013). Real-time forecasting US GDP from small-scale
factor models. Empirical Economics, 47(1), 347-364. doi: 10.1007/s00181-013-0731-4
Chun-Chu. (2011). Forecasting the Spanish Stock Market Returns with Fractional and Non-
Fractional Models. American Journal Of Economics And Business Administration, 3(4),
586-588. doi: 10.3844/ajebasp.2011.586.588
Dritsaki, D. (2015). Forecasting Real GDP Rate through Econometric Models: An Empirical
Study from Greece. Journal Of International Business And Economics, 3(1). doi:
10.15640/jibe.v3n1a2
Fildes, R., & Allen, P. (2011). Forecasting. Los Angeles, Calif.: SAGE.
11

Şen Doğan, B., & Midiliç, M. (2018). Forecasting Turkish real GDP growth in a data-rich
environment. Empirical Economics. doi: 10.1007/s00181-017-1357-8
12